下载文档原格式
实验三 圆周率的计算学号： 姓名：XX一、 实验目的1. 本实验涉及概率论、定积分、三角函数等有关知识，要求掌握计算π的三种方法及其原理。
2. 学习和掌握数学软件MATLAB 的使用方法。
二、 实验内容圆周率是一个极其驰名的数。
从有文字记载的历史开始，这个数就引起了外行人和学者们的兴趣。
作为一个非常重要的常数，圆周率最早是出于解决有关圆的计算问题。
仅凭这一点，求出它的尽量准确的近似值，就是一个极其迫切的问题了。
事实也是如此，几千年来作为数学家们的奋斗目标，古今中外一代又一代数学家为此献出了自己的智慧和劳动。
回顾历史，人们对π的认识过程，反映了数学和计算技术发展情形的一个侧面。
π的研究，在一定程度上反映这个地区或时代的数学水平。
德国数学家康托说：“历史上一个国家所算的圆周率的准确程度，可以作为衡量这个国家当时数学发展水平的指标。
”直到19世纪初，求圆周率的值还是数学中的头号难题。
1. 圆周率的计算方法古人计算圆周率，一般是用割圆法。
即用圆的内接或外切多边形来逼近圆的周长。
Archomedes 用正96边形得到35位精度；刘徽用正3072边形得到5位精度；Ludolph V an Ceulen 用正2^62边形得到了35位精度。
这种基于几何的算法计算量大，速度慢，吃力不讨好。
随着数学的发展，数学家们在进行数学研究时有意无意得发现了许多计算圆周率的公式。
下面挑选一些经典的常用公式加以介绍。
除了这些经典公式外，还有很多其他公式和由这些经典公式衍生出来的公式，就不一一列举了。
1) Machin 公式2391a r c t a n451a r c t a n 16-=π ()121...753arctan 121753--++-+-=--n x x x x x x n n 这个公式由英国天文学教授John Machin 于1706年发现。
他利用这个公式计算到100位的圆周率。
Machin 公式每计算一项可以得到1.4位的十进制精度。
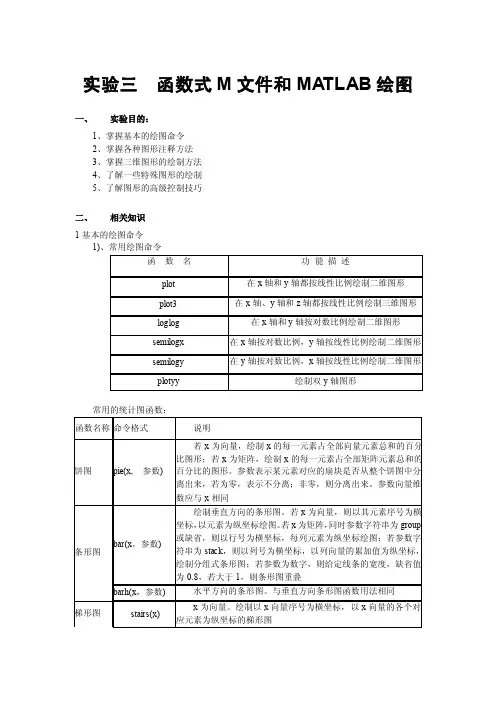
实验三函数式M文件和MA TLAB绘图一、实验目的：1、掌握基本的绘图命令2、掌握各种图形注释方法3、掌握三维图形的绘制方法4、了解一些特殊图形的绘制5、了解图形的高级控制技巧二、相关知识1基本的绘图命令1)、常用绘图命令常用的统计图函数：在MA TLAB 7中，使用plot函数进行二维曲线图的绘制>> x=0:0.1:10;>> y1=sin(x);>> y2=cos(x-2.5);>> y3=sqrt(x);>> plot(x,y1,x,y2,x,y3)3)、极坐标图形的绘制MA TLAB提供了polar(x1,x2,s)函数来在极坐标下绘制图形：（参数1角度，参数2极半径，参数3颜色和线性）>> x= 0:0.01:10;>> y1=sin(x);>> y2 = cos(x-2.5);>> polar(y1,y2,'-r+')4)、多个图形的绘制方法subplot函数可以实现多个图形的绘制：>>x = 0:.1:20;>>subplot(2,2,1)>>plot(x,sin(x));>>subplot(2,2,2);>>plot(x,cos(x))5)、曲线的色彩、线型和数据点型基本的绘图命令都支持使用字符串来给不同的曲线定义不同的线型，颜色和数据点型。
plot(x,sin(x),'-rd')图形注释对图形进行注释的方式A 图形注释“工具栏。
B 图形调色板中的注释工具C insert 菜单中的“注释”命令D 直接使用注释命令Annotation 函数Xlabel ，ylabel ，zlabel 函数 Title 函数 Colorbar 函数 Legend 函数实验内容： 一、 基础练习1、跟我练输入x,y 的值，并将它们的值互换后输出 x=input('Input x please:\n');y=input('Input y please:\n'); echo on z=x; x=y; y=z; disp(x); disp(y);echo off2、练习请求键盘输入命令keyboard ，处理完毕后，键入return ，程序将继续运行 求一元二次方程ax2 +bx+c=0的根。
数学实验—实验报告（免积分）一、实验项目：Matlab 实验三—迭代 二、实验目的和要求a. 熟悉MATLAB 软件的用户环境，掌握其一般目的命令和MATLAB 数组操作与运算函数；b. 掌握MATLAB 软件的绘图命令，能够熟练应用循环和选择结构实现各种循环选择功能；c. 借助MATLAB 软件的绘图功能，对函数的特性进行探讨，广泛联想，大胆猜想，发现进而证实其中的规律。
三、实验内容问题一：将方程535210x x x +-+=改写成各种等价的形式进行迭代 观察迭代是否收敛，并给出解释。
问题二：迭代以下函数，分析其收敛性。
4f(x)=x -a使用线性连接图、蛛网图或费根鲍姆图对参数a 进行讨论和观察，会得到什么结论？ 问题一： （1）画图 x1=-6:0.01:6; x2=-3:0.01:3; x3=-1:0.01:1;x4=-0.8:0.01:-0.75;y1=x1.^5 +5*x1.^3-2*x1+1; y2=x2.^5 +5*x2.^3-2*x2+1; y3=x3.^5 +5*x3.^3-2*x3+1; y4=x4.^5 +5*x4.^3-2*x4+1; subplot(2,2,1),plot(x1,y1) ,title('图 (1)') ,grid on, subplot(2,2,2),plot(x2,y2) ,title('图 (2)'),grid on, subplot(2,2,3),plot(x3,y3) ,title('图 (3)'),grid on, subplot(2,2,4),plot(x4,y4) ,title('图 (4)') ,grid on,-10-50510-1-0.500.514图 (1)-4-2024-400-200200400图 (2)-1-0.500.51-505图 (3)-0.8-0.78-0.76-0.74-0.72图 (4)有图可知x 的初值在（-0.78，0.76）之间 （2）构造迭代函数()x f x =53512x x x ++= 1()x f x =22215x x x x -+-= 2()x f x =24521x x x x -+-= 3()x f x =(3)迭代 设定初值0.78x =-函数1()n n x f x -=用MATLAB 编程：x(1)=-0.77;y(1)=-0.77;z(1)=-0.77; for i=2:20x(i)=(x(i-1)^5+5*x(i-1)^3+1)/2;y(i)=(-y(i-1)^5+2*y(i-1)-1)/(5*y(i-1)^2); z(i)=(-5*z(i-1)^3+2*z(i-1)-1)/(z(i-1)^4); endn=1:20subplot(221), plot(n,x), title('f(1)'); subplot(222), plot(n,y), title('f(2)'); subplot(223), plot(n,z), title('f(3)'); 结果显示：5101520-6-4-2249f(1)510152000.511.562f(2)5101520-4-2024f(3)如图显示，显然不收敛。
Matlab实验三答案实验三 MATLAB语⾔的程序设计⼀、实验⽬的：1、熟悉MATLAB程序编辑与设计环境2、掌握各种编程语句语法规则及程序设计⽅法3、函数⽂件的编写和设计4、了解和熟悉跨空间变量传递和赋值⼆、实验基本知识：1、程序流程控制语句for循环结构语法：for i＝初值：增量：终值语句1……语句nend说明：1．i＝初值：终值，则增量为1。
2．初值、增量、终值可正可负，可以是整数，也可以是⼩数，只须符合数学逻辑。
while 循环结构语法：while 逻辑表达式循环体语句end说明：1、whiIe结构依据逻辑表达式的值判断是否执⾏循环体语勾。
若表达式的值为真，执⾏循环体语句⼀次、在反复执⾏时，每次都要进⾏判断。
若表达式的值为假，则程序执⾏end之后的语句。
2、为了避免因逻辑上的失误，⽽陷⼊死循环，建议在循环体语句的适当位置加break语句、以便程序能正常执⾏。
（执⾏循环体的次数不确定；每⼀次执⾏循环体后，⼀定会改变while 后⾯所跟关系式的值。
）3、while循环也可以嵌套、其结构如下：while逻辑表达式1循环体语句1while逻辑表达式2循环体语句2end循环体语句3endelse if 表达式2(可选)语句2else(可选)语句3endend说明：1.if结构是⼀个条件分⽀语句，若满⾜表达式的条件，则往下执⾏；若不满⾜，则跳出if结构。
2．else if表达式2与else为可选项，这两条语句可依据具体情况取舍。
3．注意：每⼀个if都对应⼀个end，即有⼏个if，记就应有⼏个end。
switch-case结构语法：switch表达式case常量表达式1语句组1case常量表达式2语句组2……otherwise语句组nend说明：1．switch后⾯的表达式可以是任何类型，如数字、字符串等。
2．当表达式的值与case后⾯常量表达式的值相等时，就执⾏这个case后⾯的语句组如果所有的常量表达式的值都与这个表达式的值不相等时，则执⾏otherwise后的执⾏语句。
数学实验报告三：MATLAB 中一元函数积分的计算
1、积分有定积分和不定积分，运用函数int 可以求得符号表达式的积分．
int(f) 求函数f 对默认自由变量x 的不定积分
int(f,t) 求函数f 对符号变量t 的不定积分
int(f,a,b) 求函数f 对默认自由变量x 从a 到b 的定积分
int(f,t,a,b) 求函数f 对符号变量t 从a 到b 的定积分
2、积分应用——求面积
解方程 [x,y]=solve(‘f1=0’,‘f2=0’)
作图：ezplot(f,[x1,x2],[y1,y2]); hold on 在同一坐标系作图
写出积分表达式进行积分
3、清除变量clear 清屏clc 清除图像 clf
班级 姓名 学号 成绩
1、 求下列函数的积分
（1） ln x xdx ⎰ （2）2cos x xdx ⎰
（3）20sin d 2x x π⎰ （4）1
01x x e dx e +⎰
2、 求抛物线2x y =与直线20x y --=所围图形面积．
要求：（1）解方程，求交点
（2）作图：在同一坐标系作出这两个函数的图形
（3）写出积分表达式 进行积分计算。
实验三：数学软件MATLAB的文件设计实验目的与要求：掌握MATABLE的M文件设计的相关知识，包括变量、表达式等基本元素和流程控制、函数等语法结构。
熟练掌握M文件的类型、结构、帮助创建和编程技巧等内容。
实验内容：1、用条件控制语句和循环控制语句编写一个M文件，解决如下问题：将数组X=(2,4,5，1，-3,6,0，-2，-19，-11,1,8,8,9,7)中介于-10与10之间的元素放入数组Y，其他的放入数组Z。
代码：x=[2 4 5 1 -3 6 0 -2 -19 -11 1 8 8 9 7];n=numel(x);y=[];z=[];l=0;k=0;for i=1:nif x(i)>=-10&&x(i)<=10l=l+1;y(l)=x(i);elsek=k+1;z(k)=x(i);endendy=yz=z2、进行下述命令help elfunhelp specfunhelp elmat了解各函数的名称。
3、理解下面函数的功能，调用此函数并写出结果。
function[avg,med]=example3-4-2(u)%主函数%本函数用内部函数计算均值和中值N=length(u);avg=mean(u,n);med=median(u,n);function a=mean(v,n%)子函数%计算均值A=sum(v)/n;Function m=median(v,n)%子函数%计算中值w=sort(v);%排序if rem(n,2)==1%奇数mw((n+1)/2);elsem=(w(n/2)+w(n/2+1));end4、通过下例，理解匿名函数的定义格式，并运行之。
a=1.3;b=0.2；c=30;y@(x)a*x.^+b*x+c;fplot(y,[-25 25])function example3-5-1a(surface)Switch surfacecase’sphere’spherecase’cylinder’cylinderendshading interp在命令窗口调用example-5-1b.m函数在命令窗口键入下面的命令行example-5-1b(’sphere’)将生成单位球面键入example-5-1b(‘cylinder’)将生成单位柱面。
《数学实验》报告实验名称 matlab作业 3 学院专业班级姓名学号2011年 10月一、【实验目的】学习编辑程序来绘制几何立体图等.二、【实验任务】（一）P79 习题5绘制圆锥螺线的图像并加各种标注，圆锥螺线的参数方程为x=tcos(π/6)ty=tsin(π/6)t， (0<=t<=20π)z=2t绘制由函数x^2/9+y^2/16+z^2/4=1形成的立体图，并通过改变观测点获得该图形在各个坐标平面上的投影。
画三维曲面z=5-x^2-y^2(-2<=x,y<=2)与平面z=3的交线.（二）P79 习题7用mesh与surf命令绘制三维曲面z=x^2+3y^2的图像，并使用不同的着色效果及光照效果。
（三）P79习题8绘制由函数x^2/9+y^2/16+z^2/4=1形成的立体图，并通过改变观测点获得该图形在各个坐标平面上的投影。
（四）P79习题9画三维曲面z=5-x^2-y^2(-2<=x,y<=2)与平面z=3的交线.【实验程序】（一）t=0:pi/50:20*pi;x=t.*cos((pi/6)*t);y=t.*sin((pi/6)*t);z=2*t;plot3(x,y,z)title('ÇúÏß4x^2+4y^2=z^2')xlabel('txÖá'),ylabel('tyÖá'),zlabel('tzÖá')（二）t=-5:0.1:5;[x,y]=meshgrid(t);z=x.^2+3*y^2;%meshÃüÁîsubplot(121);mesh(x,y,z);title('meshÃüÁî');shading flat;light('position',[0,0,10])%surfÃüÁîsubplot(1,2,2);surf(x,y,z);title('surfÃüÁî');shading faceted;light('position',[0,2,10])（三）a=3;b=4;c=2;[X,Y,Z]=ellipsoid(0,0,0,a,b,c,400);subplot(221),mesh(X,Y,Z)view(3)subplot(222),mesh(X,Y,Z)view(30,30)subplot(223),mesh(X,Y,Z)view(30,0)subplot(224),mesh(X,Y,Z)view(-120,30)axis equalaxis image(四)t=-2:0.1:2;[x,y]=meshgrid(t);z1=5-x.^2-y.^2;subplot(131)mesh(x,y,z1),title('z=5-x^2-y^2')z2=3*ones(size(x));subplot(132)mesh(x,y,z2),title('z=3')r0=abs(z1-z2)<=1;zz=r0.*z2;yy=r0.*y;xx=r0.*x;subplot(133),plot3(xx(r0~=0),yy(r0~=0),zz(r0~=0),'x')三、【实验结果】（一）（二）（三）(四)【实验总结】学会使用关键字来绘制函数图象,包括加各种标注,画圆锥螺线,使用着色效果、光照效果,画椭球，并改变观测点获得不同坐标平面的投影，画曲面与平面的交线等。
实验三 MATLAB 绘图一、实验目的1．掌握二维图形的绘制。
2．掌握图形的标注3．了解三维曲线和曲面图形的绘制。
二、实验的设备及条件计算机一台（带有以上的软件环境）。
设计提示1．Matlab 允许在一个图形中画多条曲线：plot(x1，y1，x2，y2，……)指令绘制y 1 = f 1(x 1), y 2 = f 2 (x 2 )等多条曲线。
Matlab 自动给这些曲线以不同颜色。
标注可用text 函数。
2．绘图时可以考虑极坐标和直角坐标的转换。
3．三维曲线绘图函数为plot3，注意参考帮助中的示例。
三、实验内容1．生成1×10 维的随机数向量a ，分别用红、黄、蓝、绿色绘出其连线图、杆图、阶梯图和条形图，并分别标出标题“连线图”、“杆图”、“阶梯图”、“条形图”。
2、绘制函数曲线，要求写出程序代码。
(1) 在区间[0:2π]均匀的取50个点，构成向量t(2) 在同一窗口绘制曲线y1=sin(2*; y2=3cos(t+；要求y1曲线为红色点划线，标记点为圆圈；y2为蓝色虚线，标记点为星号。
(3) 分别在靠近相应的曲线处标注其函数表达式。
3.将图形窗口分成两个绘图区域，分别绘制出函数：⎩⎨⎧+-=+=1352221x x y x y 在[0,3]区间上的曲线，并利用axis 调整轴刻度纵坐标刻度，使1y 在[0,12]区间上，2y 在[-2,]区间上。
4．用mesh 或surf 函数，绘制下面方程所表示的三维空间曲面，x 和y 的取值范围设为[-3，3]。
101022y x z +-=思考题：1. 编写一个mcircle(r)函数，调用该函数时，根据给定的半径r ，以原点为圆心,画一个如图所示的红色空心圆。
（图例半径r=5）；左图参考polar函数的用法，右图绘制圆形的参数方程为x=sin （t ），y=cos （t ）。
其中，t 的区间为0~2*pi ，步长为。
2．（1）绘一个圆柱螺旋线（形似弹簧）图。
