下载文档原格式
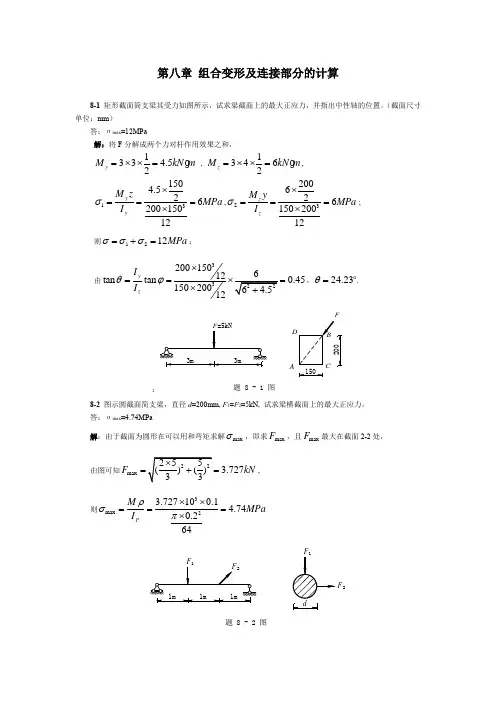
第八章 组合变形及连接部分的计算8-1 矩形截面简支梁其受力如图所示，试求梁截面上的最大正应力，并指出中性轴的位置。
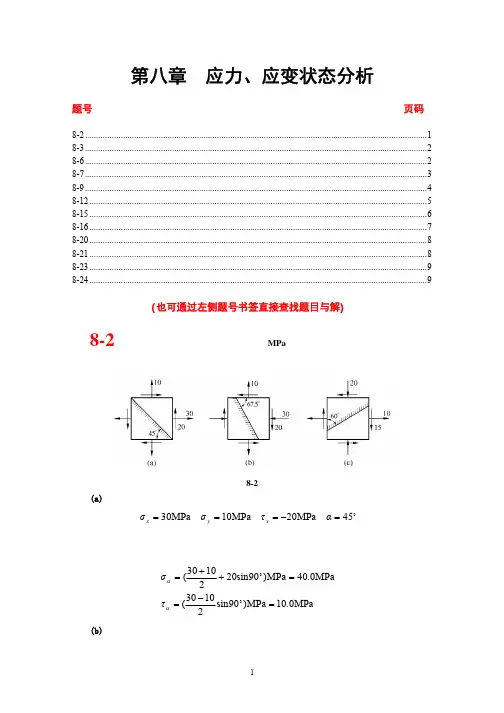
（截面尺寸单位：mm ）答：σmax =12MPa解：将F 分解成两个力对杆作用效果之和，133 4.52y M kN m =⨯⨯= , 13462z M kN m =⨯⨯=, 131504.52620015012y y M z MPa I σ⨯===⨯,2320062615020012z zM y MPa I σ⨯===⨯; 则1212MPa σσσ=+=；由3320015012tan tan 0.4515020012y zI I θϕ⨯===⨯，24.23θ=.：8-2 图示圆截面简支梁，直径d =200mm, F 1=F 2=5kN, 试求梁横截面上的最大正应力。
答：σmax =4.74MPa解：由于截面为圆形在可以用和弯矩求解max σ，即求max F ，且max F 最大在截面2-2处，由图可知max3.727F kN =, 则3max23.727100.14.740.264PM MPa I ρσπ⨯⨯===⨯A150题 8 - 1 图FF 2题 8 - 2 图8-3 图示悬臂梁，由试验测得εA =2.1×10-4，εB ＝3.2×10-4, 已知材料的E ＝200GPa ，试求P 和β值。
答：F =1.03kN,β='2131ο解：由已知74.210AA E Pa σε==⨯，76.410B B E Pa σε==⨯,又有y A z zF ly My I I σ==得y F =875N ，同理z F =535N 则F =1.03kN,'arctan()3021zyF F β== 8-4图示圆截面轴在弯矩M 和扭矩T 联合作用下，由试验测得A 点沿轴向的线应变为0ε＝5×10－4，B 点与轴线成45°方向的线应变为ε45°＝4.3×10－4。
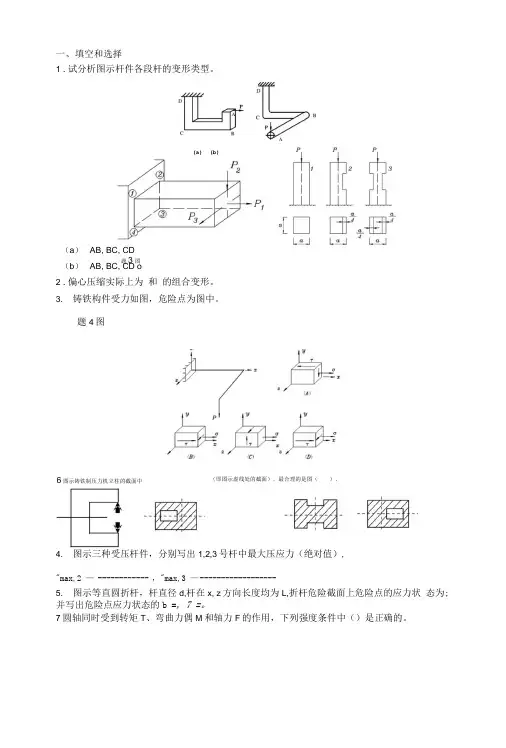
（即图示虚线处的截面），最合理的是图（ ）。
一、填空和选择1 .试分析图示杆件各段杆的变形类型。
（a ） AB, BC, CD（b ） AB, BC, CD o 2 .偏心压缩实际上为 和 的组合变形。
3. 铸铁构件受力如图，危险点为图中。
题4图4. 图示三种受压杆件，分别写出1,2,3号杆中最大压应力（绝对值）,"max,2 — ------------ ，"max,3 — ------------------5. 图示等直圆折杆，杆直径d,杆在x, z 方向长度均为L,折杆危险截面上危险点的应力状态为;并写出危险点应力状态的b =, 7 =。
7圆轴同时受到转矩T 、弯曲力偶M 和轴力F 的作用，下列强度条件中（）是正确的。
(a) (b)题3图6图示铸铁制压力机立柱的截面中d 和匕则拉杆的剪切面积是 挤压面积是50 kN9. 图示连接板中，最危险的销钉为 10, 图示连接件中，2t<6时，销钉的名义剪切应力为 名义挤压应力为二、图示悬臂梁由25b 工字钢制成，受图示荷载作用。
已知g=3kN/m, F=7kN, /=3m, [o]=170MPa,试校核其强度。
三、图示传动轴 P1=4.5KN, P2=4KN, P3=13.5KN, P4=5.2KN, Df=100mm, d=50mm,许用应(D)8.已知图示拉杆尺寸D, 题9图300 500 200力[cr] = 300MPa 。
试求：（1）画轴的受力简图；（2）做内力图（弯矩图和扭矩图, 并且内力图需与受力位置相对应）；（3）分别按第三、第四强度理论校核轴的强度。
四、图示圆轴直径 d=20mm,已知 ml=0.1KN.m, m2=0.2KN.m, m3=0.3KN.m, P=10KN,试求 轴内危险截面的主应力和最大剪应力，若材料许用应力[b] = 170MPa,按第三、第四 强度理论校核该轴的强度。
（要求画单元体）五、托架如图，已知AB 为矩形截血梁，宽度b=20mm, h=40mm,杆cd 为圆管，外径D=30mm,Z?内径d=24mm,材料的[a] = 1 60MPa,按强度要求计算该结构的许用载荷[q].（注, 杆cd 不考虑稳定性问题，只考虑强度问题），0.6m q六、图示圆截面杆受力P 和力偶m 的联合作用，今测得A 点轴向应变£o =4x10^, B 点与母线成45°方向应变句5 =3.75x101。
![周建方版材料力学习题解答[第八章]](https://img.taocdn.com/s1/m/7f09f61452d380eb62946d6f.png)
[8-1] 14号工字钢悬臂梁受力情况如图所示。
已知F2 l.OkN，试求危险截面上的最大正应力。
解：危险截面在固定端，拉断的危险点在前上角点，压断的危险点在后下角，因[8-2]矩形截面木標条的跨度1 4m ,荷载及截面尺寸如图所示，木材为杉木, 弯曲许用正应力[]12MPa , E 9GPa ,许可挠度[w] 1/200 o试校核標条的强度和刚度。
1 0.8m , Fl 2.5kN ,钢材的拉压性能相同, 故只计算最大拉应力:maxMz MyWz Wy Wz Wy式中，Wz , Wy由14号工字钢, 查型钢表得到Wz 102cm^ , Wymax79.1 io'Pa MPa79 J2 102 10 6m3 16.1 10 6 n?■ . , ■ l ・6kN/m ________A 戈HHluq习题8解：（1）受力分析COS1.6 cos26° 34 1.431(/ kN mq z q sin 1.6 sin26°340.716( kN/m)(2)内力分析My .max4qz 1 81 2-q yl 2 8(3)应力分析Mz.max-4 0.716 8-1 1.432 84 2 1.432(kN m) 4? 2.864(kN m) 最大的拉应力出现在跨中截面的右上角点， 最大压应力出现在左下角点。
M y ・ maxz.maxmax式中,160 11026322667 mm?maxWz110 16O 26469333mm^1.432 1()6 N mm2.86425 心隔（4）强度分析 因为max（5）变形分析322667 mm?469333mm310.54MPa , [ ] 12MPa ,即max［所以杉木的强度足够。
最大挠度出现在跨中，查表得:■1-60-1-1^ 17746667 (mn?)12（6）刚度分析 12屮一37546667 mm^12Wcy5qyl4 5 1.431N/mm 4000^ mm^ 384EIz 384 9 1()3 N/mn? 37546667mm^14.12mmwcz5qzl^ 5 0.716N/mm 400()4 mn? 384EIy384 9103 N/mm217746667mm° 14.94.mm (Wc/ \i4.12 214.94220,56(mm)式中，ly12因为WmaxWc 20・56(mm) , [ w]400020(mm),即 Wmax [w],200 200 所以，从理论上讲，变形过大，不符合刚度要求。
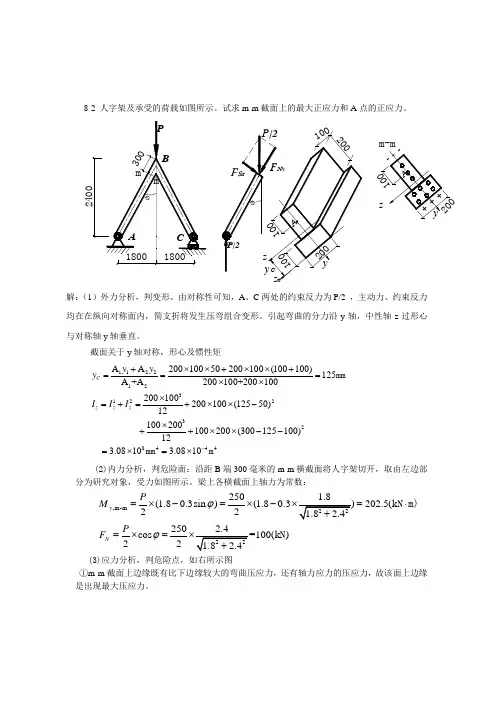
8-2 人字架及承受的荷载如图所示。
试求m-m 截面上的最大正应力和A 点的正应力。
m解：（1）外力分析，判变形。
由对称性可知，A 、C 两处的约束反力为P/2 ，主动力、约束反力均在在纵向对称面内，简支折将发生压弯组合变形。
引起弯曲的分力沿y 轴，中性轴z 过形心与对称轴y 轴垂直。
截面关于y 轴对称，形心及惯性矩1122123122328444A A 20010050200100(100100)125A +A 200100+200100200100200100(12550)12100200100200(300125100)123.0810 3.0810C z zzy y y I I I -+⨯⨯+⨯⨯+===⨯⨯⨯=+=+⨯⨯-⨯++⨯⨯--=⨯=⨯mmmm m(2)内力分析，判危险面：沿距B 端300毫米的m-m 横截面将人字架切开，取由左边部分为研究对象，受力如图所示。
梁上各横截面上轴力为常数：,m-m 250(1.80.3sin )(1.80.3202.5(k 22250cos =100(k )22y N P M P F ϕϕ=⨯-=⨯-=⋅=⨯=N m)N(3)应力分析，判危险点，如右所示图①m-m 截面上边缘既有比下边缘较大的弯曲压应力，还有轴力应力的压应力，故该面上边缘是出现最大压应力。
m mmax33410010202.510(0.30.125)(Pa) 2.5115.06MPa 117.56MPa 2(0.20.1) 3.0810N zF M y A I σ---=+⋅-⨯⨯=-⨯-=--=-⨯⨯⨯上② A 点是压缩区的点，故m m33410010202.510(0.30.1250.1)(Pa) 2.549.31MPa 51.83MPa 2(0.20.1) 3.0810N a a zF M y A I σ--=+⋅-⨯⨯=-⨯--=--=-⨯⨯⨯注意：最大拉应力出现在下边缘m mmax33410010202.5100.125(Pa) 2.582.18MPa 79.68MPa2(0.20.1) 3.0810N zF M y A I σ---=+⋅-⨯⨯=+⨯=-+=⨯⨯⨯下8-3 图示起重机的最大起吊重量为W=35kN ，横梁AC 由两根NO.18槽钢组成。
《材料力学》第8章组合变形及连接部分的计算习题解第八章组合变形及连接部分的计算习题解[习题8-1] 14号工字钢悬臂梁受力情况如图所示。
已知，F,2.5kN，l,0.8m1F,1.0kN，试求危险截面上的最大正应力。
2解:危险截面在固定端，拉断的危险点在前上角点，压断的危险点在后下角，因钢材的拉压性能相同，故只计算最大拉应力:33WW,102cmW式中，，由14号工字钢，查型钢表得到，。
故 W,16.1cmyzzy 333，2.5，10N，0.8m1.0，10N，0.8m6,,，,79.1，10Pa,79.1MPamax,,63632，102，10m16.1，10m[习题8-2] 受集度为的均布荷载作用的矩形截面简支梁，其荷载作用面与梁的纵向对称q0面间的夹角为，如图所示。
已知该梁材料的弹性模量;梁的尺寸为 ,,30E,10GPa[,],12MPa[w],l/150，，;许用应力;许用挠度。
l,4mh,160mmb,120mm试校核梁的强度和刚度。
1解:(1)强度校核0 (正y方向?) q,qcos30,2，0.866,1.732(kN/m)y0q,qsin30,2，0.5,1(kN/m) (负z方向?) z1122 出现在跨中截面 M,ql,，1.732，4,3.464(kN,m)zmazy881122 出现在跨中截面 M,ql,，1，4,2(kN,m)ymazz8811223 W,bh,，120，160,512000(mm)z6611223 W,hb,，160，120,384000(mm)y66最大拉应力出现在左下角点上:MMymaxzmax ,,，maxWWzy663.464，10N,mm2，10N,mm,,，,11.974MPa max33512000mm384000mm ,,11.974MPa,,[,]因为，，即: [,],12MPa maxmax所以满足正应力强度条件，即不会拉断或压断，亦即强度上是安全的。
(2)刚度校核=2。
即符合刚度条件，亦即刚度安全。
,0.0202m,[w],4/150,0.0267m[习题8-3] 悬臂梁受集中力F作用如图所示。
已知横截面的直径，，D,120mmd,30mm 材料的许用应力。
试求中性轴的位置，并按照强度条件求梁的许可荷载[F]。
[,],160MPa解:0 (正y方向?) F,Fcos30,0.866Fy0F,qsin30,0.5F (负z方向?) z出现在固定端截面，上侧受拉 M,Fl,0.866F，2,1.732F(N,m)zmazy出现在固定端截面，外侧受拉 M,Fl,0.5F，2,F(N,m)ymazz111,442244 I,D,2,[d，d,d],(D,34d),,,z64644643.14444 ,(120,34，30),8822419mm6411,4444I,D,2，d,(D,2d) ,,y6464643.14444 ,(120,2，30),10094119mm64IM1.732F10094119yzmax tan,,,,,,1.9816577MIF8822419ymaxz00'，即:中性轴是过大圆的圆心，与y轴的正,,arctan1.9816577,63.223,63130'向成的一条直线(分布在二、四象限)。
631332222 (沿F作用线方向) M,M，M,3F，F,2FzymaxmaxmaxI88224193z W,,,147040(mm)zD/2603M2F，10N,mmmax ,,,,160MPamax3W147040mmzF,11763N,11.763kN[F],11.763kN[习题8-4] 图示一楼梯木料梁的长度，截面为的矩形，受均布荷载作l,4m0.2m，0.1m用，。
试作梁的轴力图和弯矩图，并求横截面上的最大拉应力与最大压应力。
q,2kN/my解:以A为坐标原点，AB方向为轴的正向。
过,点，倾斜向下方向为轴的正向。
x10 (负方向:?) xq,qsin30,2，,1(kN/m)x230q,qcos30,2，,3(kN/m)y (正方向:?) y2X,4kNA、B支座的反力为:， Y,R,23kNAABN(x),,q(4,x),x,4,,杆的轴力: x1322M(x)23xqx23xx,,,,,,杆的弯矩: y22x 0 1 2 3 4N -4-3 -2 -1 0M 0 2.598 3.464 2.598 0AB杆的轴力图与弯矩图如图所示。
4x(m)001234-1-2-3-4-5N(kN)轴力图01234x(m)00.511.522.533.54M(kNm)弯矩图2M(x)N(x)(3.464x,0.866x)kN,m(4,x)kN(x),,,, ,t21WA0.1，0.2m23z，0.1，0.2m62,1500(3.464x,0.866x),50(4,x)2 ,5196x,1299x,200，50x2 (kPa) ,,1299x，5246x,200d(x),t令,,2598x，5246,0，得:当时，拉应力取最大值: x,2.019mdx2 ,,,1299，2.019，5246，2.019,200,5096.5(kPa),5.097MPatmax2M(x)N(x)(3.464x,0.866x)kN,m(4,x)kN(x),,,,,,, c21WA0.1，0.2m23z，0.1，0.2m62,,1500(3.464x,0.866x),50(4,x)52 ,,5196x，1299x,200，50x2 ,1299x,5146x,200d(x),t令，得:当时，压应力取最大值: ,2598x,5146,0x,1.981mdx2 ,,1299，1.981,5146，1.981,200,,5296.5(kPa),,5.297MPacmax[习题8-5] 图示一悬臂滑车架，杆为18号工字钢，其长度为m。
试求当荷载AB作用在AB的中点D处时，杆内的最大正应力。
设工字钢的自重可略去不计。
解:18号工字钢，，AB杆系弯压组合变形。
0MFcos30中BC,,,, cmaxWAl0F,25kN:， M,0Fsin30,l,F,,0BC,ABC2l2.60 M,Fsin30,,25，0.5，,16.25(kN,m)BC中223325，10，N316.25，10N,m62 ,,,,,,(87.83，7.07)，10Pa,,94.9MPacmax,43421.85，10m30.6，10md,3md,2m[习题8-6] 砖砌烟囱高，底截面m,m的外径，内径，自重h,30m12P,2000kNq,1kN/m，受的风力作用。
试求: 1(1)烟囱底截面上的最大压应力;h,4mP,1000kN(2)若烟囱的基础埋深，基础及填土自重按计算，土壤的许用01 [,],0.3MPa压应力，圆形基础的直径D应为多大,6注:计算风力时，可略去烟囱直径的变化，把它看作是等截面的。
解:烟囱底截面上的最大压应力:==土壤上的最大压应力:即即解得:m[习题8-7] 螺旋夹紧器立臂的横截面为和矩形，如图所示。
已知该夹紧器工作时承受a，b的夹紧力，材料的许用应力[,],160MPa，立臂厚，偏心距F,16kNa,20mm。
试求立臂宽度。
e,140mmb解:立柱是拉弯构件。
最大拉应力为:FFeFe16 ,,，,(，)tmax21ababb2ab6，1600016140,， ()2b20b1840,， 800()2bb正应力强度条件:7,,[,] tmax1840 800(，),1602bb2 b,5b,4200,0解得: b,67.356mm[习题8-8] 试求图示杆内的最大正应力。
力F与杆的轴线平行。
解:(1)求T形截面的形心位置22,a,8a，2a,4ay,,0 形心在y轴上， C228a，4a(2)把力F先向y轴平移，产生一个; M,,F,2a,,2FayM,,F,2a,,2Fa然后，再把F向z轴平移，又产生一个。
z故，T形截面的杆件是拉伸与双向弯曲的组合变形构件。
(3)判断最大拉应力与最大压应力出现的位置MM 由、的方向(正负号)可知，A点处拉应力最大，B点处压应力最大。
yz(4)计算最大拉应力113223224 I,[,4a,(2a)，a,8a]，[,a,(4a)，(2a),4a],32az12128MzMyFyAzA ,,，，,,tAmaxAIIyzF2aF,2a2aF,2a151FF ,，，,,0.5722442212a11a32a264aa(5)计算最大压应力MzMyFyBzA,,,,,,cB max AIIyzF2aF,0.5a2aF,4a17FF ,,,,,,,0.2582442212a11a32a66aaF 故杆内的最大正应力是:。
,,,,0.572tAmax2a[习题8-9] 有一高为、厚为的混凝土墙，浇筑于牢固的基础上，用作挡水用的1.2m0.3m小坝。
试求:(1)当水位达到墙顶时，墙底处的最大拉应力和最大压应力(高混凝土的密度为332.45，10kg/m);(2)如果要求混凝土中没有拉应力，试问最大许可水深为多大, h解:(1)求墙底处的最大拉应力和最大压应力沿墙长方向取作为计算单元，则墙的重力为: 1mG,(0.3，1，1.2)，2.45，9.8,8.6436(kN) (?)作用在墙底处的水压力为:q,,,h，1,9.8，1.2，1,11.76(kN/m)墙底处的弯矩:11 M,(，11.76，1.2)，，1.2,2.8224(kN,m)23混凝土墙为压弯构件，墙底的应力为:GM8.6436kN2.8224kN,m(右) ,,,,,,,,,216.972kPa,,0.217MPacmax21AW0.3，1m23z，1，0.3m6GM8.6436kN2.8224kN,m(左) ,,,，,,，,159.348kPa,0.159MPatmax21AW0.3，1m23z，1，0.3m69(2)求混凝土中没有拉应力时的水深 h作用在墙底处的水压力为:q,,,h，1,9.8，h，1,9.8h(kN/m)墙底处的弯矩:114.93 M,(，9.8h，h)，，h,h(kN,m)2334.93hkN,mGM8.6436kN33 ,,,，,,，,,28.812，108.9h,0tmax21AW0.3，1m23z，1，0.3m63 ,28.812，108.9h,0h,0.642(m)故当时，混凝土中不出现拉应力。
h,0.642m[习题8-10] 受拉构件形式状如图，已知截面尺寸为，承受轴向拉力40mm，5mm。
现拉杆开有切口，如不计应力集中影响，当材料的时，试确定[,],100MPaF,12kN切口的最大许可深度，并绘出切口截面的应力变化图。
