九年级数学图形的位似课件

思考：是否相似图形都是位似图形？
2 判断下面的正方形是不是位似图形？
A
D
E
F
（1）
B
C
G
显然，位似图形是相似图形的特殊情
形位.似相图似形图与形相不似一图定形有是什位么似关图系形？，可位 似图形一定是相似图形
思考：位似图形有何性质？
不是位似图形
3 如果∆OAB和 ∆OCD是位似图形，那么
AB∥CD吗？为什么？
A
O.
C
B
C’
B’
思考：还有没其他作法？
C’
B’
A
. O
B
C
A'
如果位似中心位于△ABC内部呢？ （课后我们还可以试一试。尽量取不 不同的位似中心。）在三角形一边的 一点上或在三角形一个顶点上呢。
位似图形的画法 A
以0为位似中心把△ABC
在同侧缩小为原来的一半。
B
步骤：
A’
1、画出的位置关系去探究。
对应边平行
概念与性质
1．位似图形的概念
如果两个图形不仅相似，而且每组对应点 所在的直线都经过同一点，对应边互相平 行，那么这样的两个图形叫做位似图形,这 个点叫做位似中心。
概念与性质
2. 位似图形的性质
OA 从第 (1)，(2)图中，我们可以看到，△OAB∽△O A′B′,则OA′ ＝
• 若△ABC与△A’B’C’的相似比为：1:2， 则OA：OA’=（ 1:2 ） OA:OA’ =OB:OB’ =OC:OC’（=1:2）
A’
AB
B’
O C C’
例1．如图，已知△ABC和点O.以O为位似中心，求作 △ABC的位似图形，并把△ABC的边长扩大到原来的两倍.

位似的性质
位置关系： （1）位似图形对应点的连线交于一点O；
（2）位似图形的对应边相互平行或在同一条直线上。 （3）位似图形每组对应点到位似中心的距离之比都相等；
数量关系： （4）位似图形一定是相似图形，且位似比等于相似比。
画位似图形
我画一个三角形不小心画得很大， 需要把它按比例缩小，该用什么办法呢 ？
位似图形每组对应点到位似 中心的距离之比都相等
位似图形是相似图形，并且 两图形的相似比等于位似比
位似的性质
B
’
A
C
O
C
B
’
A
位似图’ 形的对应边有没有
特殊的位置关系呢？
位似的性质
证明：
B’
∵⊿OBC∽⊿OB′C′
A C
∴∠OBC = ∠OB′C′ ∴BC∥B′C′
根据内错角相等 两直线平行
O
同理，AB∥A′B′ ，AC∥A′C′。
D’(-8,-2) C’(-10,-8)
B’(4,6)
C’(10, 8)
B(2,3)
C(5,4)
A(1,1) A’(2,2) D(4,1)
D’(8,2)
A’(-2,-2)
B’(-4,-6)
位似的坐标表示
在平面直角坐标系中，以O为位似中心， 以k为相似比画出位似图形，新图形顶点 的横纵坐标是原图形顶点的横纵坐标的 ±k倍。
电影胶片
答：当银幕在距离光源8米时， 放映的图像刚好布满整个银幕。
图形 相似 关系 变换
课堂总结
研究路径 类比全等变化的研究路径
研究方法 观察，操作，归纳
研究内容 定义，性质，画图，坐标表示，应用
课堂总结
全等 图形

位似多边形的定义：
如果两个相似多边形任意一组对应顶点P，P̍ 所 在的直线都经过同一点O,且OP ̍ =k· OP （k≠0）,那 么这样的两个多边形叫做位似多边形，点O叫做位似 中心.其中k为这两个相似多边形的相似比.
位似多边形三层意思 1.两个多边形相似.
2.对应点的连线都经过同 一点. 3.任意一组对应点与位似
分别取点D,E,F,使OD = 2OA,OE
= 2OB,OF = 2OC;
F
3.顺序连接D,E,F,则△DEF与
E
△ABC位似,相似比为2.
D
A
B
O
C
随堂练习
已知点O在△ABC内，以点O为位似中心画一个三角形， 使它与△ABC位似，且相似比为1/2.
课堂小结
定义
如果两个相似多边形任意一组对应顶点P，P ̍ 所在的直 线都过同一点O,且OP ̍ =k· OP（k≠0）,那么这样的两
OB=5.4cm OE=3cm OB＇=2.54cm OE＇=1.4cm
C
D
D' C'
OC=4.9cm AB=1.4cm
OC＇=2.3cm A＇B＇=0.66cm
位似图形的概念
（1）动手用直尺连的连线交于一点O
进行演示
此时称五边形ABCDE与五边形A´B´C´D´E´是位似图形.
中心的距离之比值是一个
定值. A
A'
E
B
B'
E'
O
D C
D' C'
观察与思考 它们都是相似五边形 它们都是位似多边形吗？ 为什么？
如果两个相似多边形任意一组对应顶点P，P̍ 所 在的直线都经过同一点O,且OP ̍ =k· OP （k≠0）,那 么这样的两个多边形叫做位似多边形，点O叫做位似 中心.其中k为这两个相似多边形的相似比.

E
内
E' O C'
部
A' B'
A
B
知识精讲
2. 位似图形的性质
（1）对应点所在的直线经过位似中心；
（2）任意一组对应点到位似中心的距离之比等于相似比；
（3）对应边平行或在同一条直线上.
D
′ ′′
=
.


D'
O
C'
E'
A'
D
C
E
B'
B
①
A
′ ′′
=
.


C
E
D'C'
E'
A A'OB' B
②
知识精讲
3. 位似图形的画法（将一个图形放大或缩小）
（1）确定位似中心和图形上的关键点；
（2）连接位似中心与关键点并延长所得线段；
（3）根据相似比确定位似图形上的关键点；
A'
（4）顺次连接位似图形上的关键点，得到位似图形.
A
画一个△A′B ′C ′，使它与∆位似，且相似比为2.
C'
C
O
B
′
分析： 设 = .
由矩形的周长
矩形与矩形′ ′ ′是位似图形


=
′ ′
D'
D
A
C'
C
B
用表示的长
用表示AB ′ , ′的长
B'
典例精讲
【例题3】如图，矩形与矩形′ ′ ′是
位似图形，为位似中心.已知矩形的周长为
24，′ = 4，′ = 2，求, 的长.

位似多边形
任意一组对应顶点 P ，P'所在
OP'＝ k ·OP ( k ≠0)
，点 O 叫做
课时学业质量评价
位似中心
，那么这样的两个
.
⁠
第1课时
位似图形
知识梳理
课时学业质量评价
1. 如图，已知△ ABC 与△ DEF 位似，位似中心点为 O ，且△ ABC 与△
DEF 的周长之比是4∶3，则 AO ∶ DO 的值为(
C. 16
B. 12
1
2
3
4
D. 20
5
6
C
)
第1课时
位似图形
知识梳理
课时学业质量评价
3. 如图，六边形 ABCDEF 与六边形 A1 B1 C1 D1 E1 F1是位似图形，点 O

为位似中心， OD ＝ OD1，则 A1 B1∶ AB 为(

A. 2∶3
D
第3题图
C. 1∶2
B. 3∶2
1
2
3
B
)
第1题图
A. 4∶7
B. 4∶3
C. 3∶4
1
2
3
4
5
D. 16∶9
6
第1课时
位似图形
课时学业质量评价
知识梳理
2. 如图，△ ABC 与△ A1 B1 C1位似， A1， B1， C1分别为 OA ， OB ， OC
的中点，若△ A1 B1 C1面积是4，则△ ABC 的面积为(
A. 4
第2题图
点D，E，F，则△DEF与△ABC位似，且类
似比为 2.
图5
探究新知
做一做
用以下方法可以近似地把一个不规则图形放大：

E
B
· CC′、DD′ 、EE′是否也都经 O
过点O？
C
D
D
C
OA , OB , OC , OD , OE 有什么关系？ A
OA OB OC OD OEOA Oຫໍສະໝຸດ OC ODA EB
E
B
· OA OB OC OD O OE AB
C
D
D
C
k.
OE AB
合作探究
A
位似图形的概念
一般地，如果两个类
突破重难点
1.对于平面图形上的任意两点P，Q，如果经 过某种变换得到新图形上的对应点P′， Q′，保持PQ=P′Q′，我们把这种变换称 为“等距变换”，下列变换中不一定是等 距变换的是（ D ） A．平移 B．旋转 C．轴对称 D．位似
2.如图，在平面直角坐标中，正方形ABCD与正方 形BEFG是以原点O为位似中心的位似图形，且类 似比为 1 ，点A，B，E在x轴上，若正方形
3
BEFG的边长为6，则C点坐标为（ A ） A．（3，2） B．（3，1） C．（2，2） D．（4，2）
3.已知△ABC是正三角形，正方形EFPN的顶点E、F在 边AB上，顶点N在边AC上． （1）如图，在正三角形ABC及其内部，以点A为位 似中心，画出正方形EFPN的位似正方形 E′F′P′N′，且使正方形E′F′P′N′的面积 最大（不写画法，但要保留画图痕迹）； （2）若正三角形ABC的边长为 3+2 3 ，则（1）中 画出的正方形E′F′P′N′的边长为______3__.
2．选取一个图形，在图形外取一点．
3．将系在一起的橡皮筋的一端固定在定点，把 一只铅笔固定在橡皮筋的另一端．
4．拉动铅笔，使两根橡皮筋的结点沿所选图形 的边缘运动，当结点在已知图形上运动一圈 时，铅笔就画出了一个新的图形．

OA：OA'
1：4 ,那么
S ：S 四边形ABCD
四边形A' B' C' D'
__1_:1_6__ .
课堂小结
位似
1.位似图形的概念. 2.位似与相似的关系. 3.位似图形的性质.
再见
似比又叫位似比.
A
位似中心：点O 相似比或位似比：EF FG HE
AB BC DA
ห้องสมุดไป่ตู้
E
B
O
F
HD
G
C
探究新知
结论： ①位似图形一定是相似图形. ②相似图形不一定是位似图形.
D'
C'
D
C
O
A'
A B'
B
探究新知
位似的特征： 1.位似是一种具有位置关系的相似. 2.位似图形是相似图形的特殊情形. 判断位似图形时，要注意首先它们必须是相似图形， 其次每一对对应点所在直线都经过同一点．
探究新知
①④对位应似线中段心有可可能能位平于行两，个也图可形能的共内线部.，也可能在两图形 ②的两公个共位顶似点图上形，的还位可似能中在心两只个有图一形个的.外部. ③⑤两每个组位对似应图点形到可位能似位中于心位的似距中离心之的比两都侧等，于也相可似能比位. 于 本位质似区中别心：的位一似侧多. 边形是具有特殊位置关系的相似多边形.
巩固新知
1.两个位似多边形中的对应角__相__等__,对应线段__成__比__例__, 对应顶 点的连线必经过___位__似__中__心___.
2.位似多边形上某一对对应点到位似中心的距离分别为5和10， 则它们的相似比为____1_:2_____.
3.四边形ABCD和四边形 A' B' C' D' 位似，O为位似中心，若

E′
D′
D
E
O
A
A′
B
C′
A
C
B′
C′
O
B
C
B′
A′
归纳：
1. 位似图形的对应角相等，对应边成比例，周长比
等于相似比，面积比等于相似比的平方；
2. 位似图形的对应点的连线相交于一点，即经过位似中心；
3. 位似图形的对应边互相平行或在同一条直线上；
4. 位似图形上任意一对对应点到位似中心的距离之比等
于相似比.
例2 如图所示，四边形ABCD 和四边形A′ B′ C′ D′位似，相似比1 ＝ 2，四边
形A′ B′ C′D′和四边形A″ B″ C″D″位似，相似比2 ＝ 1. 则四边形A″ B″ C″ D″
和四边形ABCD 是位似图形吗？如果是，请说明理由并求出相似比.
解：∵ 四边形ABCD 和四边形A′ B′ C′ D′位似，
E
OD;在射线OA、OB、OC、
H
A
OD上分别取点D、E、F,使
D
O
B
C
OE = 2OA , OF = 2OB , OG =
2OC , OH = 2OD;顺次连结E、
F、G、H,使正方形ABCD与
F
G
5.如图所示，四边形ABCD的一个位似图形是四边形A′ B′ C′ D′ ，
且A,B,C,D的对应点分别是A′ ,B′ ,C′ ,D′. 图中给出了AB的对应
似中心的位似图形，且

′
＝


＝
′
′
＝

′
；五边形ABCDE 与五


边形A′ B′ C′ D′ E′是以点O 为位似中心的位似图形，且′ ＝ ′ ＝

B
B`
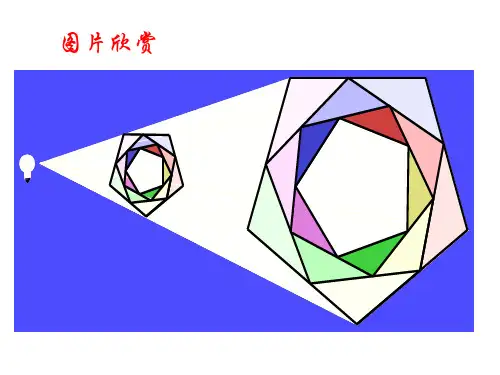
每一组对应点的连线都经过镜头中心点O
下面两个多边形相似，将两个图形的顶点相连，观察发现连接的直线相交于点O. 有什么关系？
如果两个相似多边形每组对应点所在的直线都经过同一个点O，且每组对应点与O 点的距离之比都等于一个定值k，例如OA′=k·OA（k≠0），那么这样的两个多边形叫做位似多边形，点O叫做位似中心， k 就是这两个相似多边形的相似比。
利用位似可以把一个图形放大或缩小
3.拉动铅笔，使结点沿图形的边缘移动一周，这样铅笔就画出一个新的图形。试试看，它们相似吗？
1.图中两个四边形是位似图形，它们的位似中心是（ ） A. 点M B. 点N C. 点O D. 点P
3.下列说法中：①位似图形一定是相似图形；②相似图形一定是位似图形；③两个位似图形若全等，则位似中心在两个图形之间；④若五边形ABCDE 与五边形A ′B ′C ′D ′E ′位似，则在五边形中连线组成的△ABC与△A ′B ′C ′也是位似的．正确的个数是（ ） A. 1 B. 2 C. 3 D. 4
解：画射线OA,OB,OC;在射线OA,OB,OC上分别取点D,E,F,使OD = 2OA,OE = 2OB,OF = 2OC;顺序连接D,E,F,使△DEF与△ABC位似,相似比为2.
想一想：你还有其他的画法吗？
A
B
C
F
E
D
O
A
B
C
画法二：△ABC与△DEF异侧.
解：画射线OA、OB、OC;沿着射线OA、OB、OC反方向上分别取点D、E、F,OD = 2OA,OE = 2OB,OF = 2OC;顺次连结D、E、F,使△DEF与△ABC位似,相似比为2.
4.已知点O 在△ABC 内，以点O 为位似中心画一个三角形，使它与△ABC 位似，且相似比为 .

D．OA1∶A1A＝2∶3
例题欣赏2：：
在直角坐标系中，四边形OABC的 顶点坐标分别为O（0,0），A（ 6,0），B（3,6），C（-3,3）.以 原点O为位似中心画一个四边形， 使它与四边形OABC位似，且类似 比是2:3。（自己动手画另一个图 形）
y
原坐标 O(0,0) 8 A(6,0)
标是 (D )
，则点 B1)
B．(－2，－3)
C．(2，3)或(－2，－3)
D．(3，2)或(－3，－2)
通过本节课的学习，你在知识上和方法上 有哪些收获？请说说看
1、位似图形、位似中心、类似比的定义。 2、在直角坐标系中，以O为位似中心的两个位 似多边形的坐标和类似比之间有什么关系？
B(3,6)
横纵坐标×-32 O′(0,0) A′(-4,0) B′(-2,-4)
6
B
C(-3,3) C′(2,-2)
4
C
2
以原点O为位 似中心，与 四边形OABC
类似比为2：
- - - -2 O 2 4 6 8 x 3的位似图形
8 64 -
有两个，它
原坐标 横纵坐标×32
24-
们关于原点 成中A 心对称。
问题2：
OA',OB',OC',OD',OE' OA OB OC OD OE'
有什么关系？
位似概念：
如果两个类似多边形每组对应点所在的 直线都经过同一个点O且每组对应点与
与O 点的距离之比都等于一个定值k， 例如OA′=k·OA（k≠0），那么这样的
两个多边形叫做位似多边形，点O叫做 位似中心。
位似比与类似比的关系
位似多边形上任意一对对应点到位似 中心的距离之比k等于类似比。