【小学四年级奥数讲义】 二进制

一、数的进制1．十进制：我们常用的进制为十进制，特点是“逢十进一”．在实际生活中，除了十进制计数法外，还有其他的大于1的自然数进位制．比如二进制，八进制，十六进制等． 2．二进制：在计算机中，所采用的计数法是二进制，即“逢二进一”．因此，二进制中只用两个数字0和1．二进制的计数单位分别是1、21、22、23、……，二进制数也可以写做展开式的形式，例如100110在二进制中表示为：(100110)2=1×25+0×24+0×23+1×22+1×21+0×20．二进制的运算法则：“满二进一”、“借一当二”，乘法口诀是：零零得零，一零得零，零一得零，一一得一．注意：对于任意自然数n,我们有n 0=1． 3．k 进制：一般地，对于k 进位制，每个数是由0，1，2，，1k -（）共k 个数码组成，且“逢k 进一”．1k k >（）进位制计数单位是0k ，1k ，2k ，．如二进位制的计数单位是02，12，22，，八进位制的计数单位是08，18，28，．4．k 进位制数可以写成不同计数单位的数之和的形式1110110n n n n k n n a a a a a k a ka k a ---=⨯+⨯++⨯+（）十进制表示形式：1010101010n n n n N a a a --=+++；二进制表示形式：1010222n n n n N a a a --=+++；为了区别各进位制中的数，在给出数的右下方写上k ，表示是k 进位制的数 如：8352（），21010（），123145（）,分别表示八进位制，二进位制，十二进位制中的数． 5．k 进制的四则混合运算和十进制一样先乘除，后加减；同级运算，先左后右；有括号时先计算括号内的．二、进制间的转换：一般地，十进制整数化为k 进制数的方法是：除以k 取余数，一直除到被除数小于k 为止，余数由下到上按从左到右顺序排列即为k 进制数．反过来，k 进制数化为十进制数的一般方法是：首先将k 进制数按k 的次幂形式展开，然后按十进制数相加即可得结果． 如右图所示:知识框架进位制【例 1】 把9865转化成二进制、五进制、八进制，看看谁是最细心的．【巩固】 852567(((=== ） ） ）；【例 2】 将二进制数2(11010.11)化为十进制数为多少？【巩固】 同学们请将258(11010101),(4203),(7236)化为十进制数，看谁算的又快又准．例题精讲【例 3】 二进制数10101011110011010101101转化为8进制数是多少？【巩固】 将二进制数11101001．1011转换为十六进制数．【例 4】 ①222(101)(1011)(11011)⨯-=________；②2222(11000111(10101(11(-÷=））） ）；③88888(63121)(1247)(16034)(26531)(1744)----=________；【巩固】 ①在八进制中，1234456322--=________；②在九进制中，1443831237120117705766+--+=________．【例 5】 若(1030)140n =，则n =________．【巩固】 在几进制中有413100⨯=？【例 6】有个吝啬的老财主，总是不想付钱给长工．这一次，拖了一个月的工钱，还是不想付．可是不付又说不过去，便故作大方地拿出一条金链，共有7环．对长工说：“我不是要拖欠工资，只是想连这一个月加上再做半年的工资，都以这根金链来付．”他望向吃惊的长工，心中很是得意，“本人说话，从不食言，可以请大老爷作证．”大老爷可是说一不二的人，谁请他作证，他当作一种荣耀，总是分文不取，并会以命相拼也要兑现的．这越发让长工不敢相信，要知道，这在以往，这样的金链中的一环三个月的工钱也不止．老财主越发得意，终于拿出杀手锏：“不过，我请大老爷作证的时候，提到一项附加条件，就是这样的金链实在不能都把它断开，请你只能打开一环，以后按月来取才行！”当长工明白了老财主的要求后，不仅不为难，反倒爽快地答应了，而且，从第一个月到第七个月，顺利地拿到了这条金链，你知道怎么断开这条金链吗？【巩固】现有1克，2克，4克，8克，16克的砝码各1枚，在天平上能称多少种不同重量的物体？【例 7】如果只许在天平的一边放砝码，要称量100g以内的各种整数克数，至少需要多少个砝码？【巩固】如果允许在天平的两边放砝码，要称量100g以内的各种整数克数，至少需要多少个砝码？【例 8】 有10箱钢珠，每个钢珠重10克，每箱600个．如果这10箱钢珠中有1箱次品，次品钢珠每个重9克，那么，要找出这箱次品最少要称几次?【巩固】 一些零件箱，每个零件10g ，每箱600个，共有10箱，结果发现，混进了几箱次品进去，每个次品零件9克，但从外观上看不出来，聪明的你能只称量一次就能把所有的次品零件的箱子都找出来吗？【例 9】 已知正整数N 的八进制表示为8(12345654321)N ，那么在十进制下，N 除以7的余数与N 除以9的余数之和是多少？【巩固】 在8进制中，一个多位数的数字和为十进制中的68，求除以7的余数为多少？【例 10】在美洲的一个小镇中，对于200以下的数字读法都是采取20进制的．如果十进制中的147在20进制中的读音是“seyth ha seyth ugens”，而十进制中的49在20进制中的读音是“naw ha dew ugens”，那么20进制中读音是“dew ha naw ugens”的数指的是十进制中的数____________．【巩固】一个自然数，在3进制中的数字和是2007，它在9进制中的数字和最小是，最大是．课堂检测【随练1】某数在三进制中为12120120110110121121，则将其改写为九进制，其从左向右数第1位数字是几? 【随练2】算式153********⨯=是几进制数的乘法？【随练3】茶叶店老板要求员工提高服务质量，开展“零等待”活动，当顾客要买茶叶的时候，看谁最快满足顾客的需要则为优秀．结果有一个员工总是第一名，而且顾客到他那儿不需要等待．原来他把茶叶先称出若干包来，放在柜台上，顾客告诉他重量，他就拿出相应重量的茶叶．别的伙计看在眼里，立即学习，可是柜台上却放不下许多包．奇怪的是，最佳员工的柜台上的茶叶包裹却不是很多．于是有员工去取经，发现最佳员工准备的茶叶数量是：1，2，4，8，16，32，64，128，256．你能解释一下其中的道理么?这些重量可以应付的顾客需要的最高重量是多少？【随练4】 古代英国的一位商人有一个15磅的砝码，由于跌落在地碎成4块，后来，称得每块碎片的重量都是整磅数，而且可以用这4块来称从1至15磅之间的任意整数磅的重物（砝码只能放在天平的一边）．那么这4块砝码碎片各重 ， ， ，【作业1】 计算4710(3021)(605)()+= ；【作业2】 在几进制中有12512516324⨯=？【作业3】 向电脑输入汉字，每个页面最多可输入1677个五号字．现在页面中有1个五号字，将它复制后粘贴到该页面，就得到2个字；再将这2个字复制后粘贴到该页面，就得到4个字．每次复制和粘贴为1次操作，要使整个页面都排满五号字，至少需要操作 次．家庭作业【作业4】 成语“愚公移山”比喻做事有毅力，不怕困难．假设愚公家门口的大山有80万吨重，愚公有两个儿子，他的两个儿子又分别有两个儿子，依此类推．愚公和它的子孙每人一生能搬运100吨石头．如果愚公是第1代，那么到了第 代，这座大山可以搬完．（已知10个2连乘之积等于1024）【作业5】 10个砝码，每个砝码重量都是整数克，无论怎样放都不能使天平平衡，这堆砝码总重量最少为_________克．【作业6】 计算机存储容量的基本单位是字节，用B 表示，一般用KB 、MB 、GB 作为存储容量的单位，它们之间的关系是1012KB B =，1012MB KB =，1012GB MB =．小明新买了一个MP3播放器，存储容量为256MB ，它相当于_____B ．。

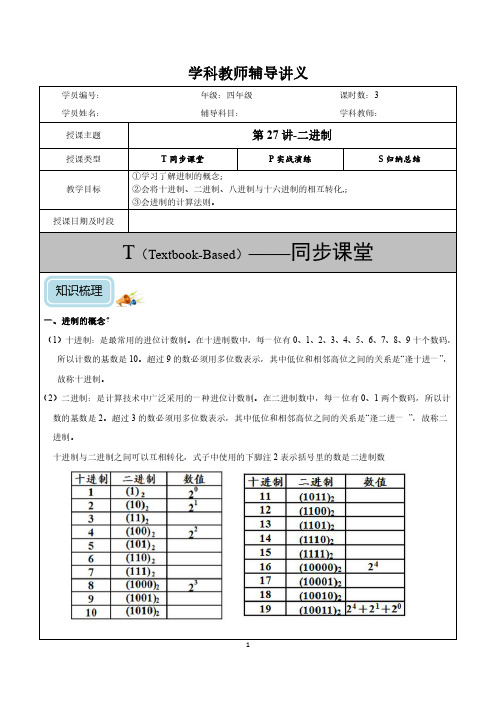
学科教师辅导讲义知识梳理（3）八进制：在八进制数中，每一位有0、1、2、3、4、5、6、7八个数码，所以计数的基数是8。

超过7的数必须用多位数表示，其中低位和相邻高位之间的关系是“逢八进一”，故称八进制。

（4）十六进制：在十六进制数中，每一位有0、1、2、3、4、5、6、7、8、9、A(表示10)、B(表示11)、C(表示12)、D(表示13)、E(表示14)、F(表示15)十六个数码，所以计数的基数是16。

超过15的数必须用多位数表示，其中低位和相邻高位之间的关系是“逢十六进一”，故称十六进制。

二、十进制与n 进制的转化1、将十进制数转换为等值的n 进制数(n≥2)时，整数部分采用“除n 倒取余数法”。

例如：整数()10107转换成二进制采用“除2倒取余数法”，得()()1021071101011=2、将n 进制数(n≥2)转换为等值的十进制数时，只要将n 进制数展开，然后将所有各项的数值按十进制数相加，就可以得到等值的十进制数了。

例如：()()()21810101231828183=⨯+⨯+=，式子中使用的下脚注8表示括号里的数是八进制数。

()()()21161010011160161512831B F =⨯+⨯+⨯=，式子中使用的下脚注16表示括号里的数是十六进制数。

3、二进制数的计算法则：（1）加法法则：0＋0=00＋1=11＋0=11＋1=10（2）乘法法则：0×0=00×1=01×0=01×1=1典例分析例6、把十进制数251改成16进制数。

例7、把二进制数()2110改写成十进制数。

例8、把二进制数()2110改写成八进制数例9、计算()()22101111+例10、计算()()22110111⨯你能用十进制计算来检验上面的计算吗？例11、计算()()221111101÷实战演练3、计算下列式子（1）()()2210110+（2）()()22110101111-（3）()()22111011+4、计算下列式子（1）()()2211010⨯（2）()()2211100100÷（3）()()22101111⨯（4）()()221001011÷5、已知：22241x y z++=，不同的字母代表不同的数字，则三位数xyz =__________.课后反击1、分别把下列各数转换成十进制数。

1. 了解进制；2. 会对进制进行相应的转换；3. 能够运用进制进行解题一、数的进制1.十进制：我们常用的进制为十进制，特点是“逢十进一”。

在实际生活中，除了十进制计数法外，还有其他的大于1的自然数进位制。

比如二进制，八进制，十六进制等。

2.二进制：在计算机中，所采用的计数法是二进制，即“逢二进一”。

因此，二进制中只用两个数字0和1。

二进制的计数单位分别是1、21、22、23、……，二进制数也可以写做展开式的形式，例如100110在二进制中表示为：(100110)2=1×25+0×24+0×23+1×22+1×21+0×20。

二进制的运算法则：“满二进一”、“借一当二”，乘法口诀是：零零得零，一零得零，零一得零，一一得一。

注意：对于任意自然数n ,我们有n 0=1。

3.k 进制：一般地，对于k 进位制，每个数是由0，1，2，，1k -（）共k 个数码组成，且“逢k 进一”．1k k >（）进位制计数单位是0k ，1k ，2k ，．如二进位制的计数单位是02，12，22，，八进位制的计数单位是08，18，28，．4.k 进位制数可以写成不同计数单位的数之和的形式 1110110n n n n k n n a a a a a k a ka k a ---=⨯+⨯++⨯+（）十进制表示形式：1010101010n n n n N a a a --=+++； 二进制表示形式：1010222n n n n N a a a --=+++；为了区别各进位制中的数，在给出数的右下方写上k ，表示是k 进位制的数如：8352（），21010（），123145（）,分别表示八进位制，二进位制，十二进位制中的数．5.k 进制的四则混合运算和十进制一样先乘除，后加减；同级运算，先左后右；有括号时先计算括号内的。

二、进制间的转换：知识点拨教学目标5-8-2.进制的应用一般地，十进制整数化为k进制数的方法是：除以k取余数，一直除到被除数小于k为止，余数由下到上按从左到右顺序排列即为k进制数．反过来，k进制数化为十进制数的一般方法是：首先将k进制数按k的次幂形式展开，然后按十进制数相加即可得结果．如右图所示:八进制十进制二进制十六进制例题精讲模块一、进制在生活中的运用【例1】有个吝啬的老财主，总是不想付钱给长工。

第12讲 进制问题【学习目标】1、学习二进制、八进制与十六进制；2、会进制的计算与转换。

【知识梳理】1、十进制：低位和相邻高位之间的关系是“逢十进一”，故称十进制；2、二进制：低位和相邻高位之间的关系是“逢二进一 ”，故称二进制；3、八进制：低位和相邻高位之间的关系是“逢八进一”，故称八进制；4、十六进制：低位和相邻高位之间的关系是“逢十六进一”，故称十六进制。

十六个数码：0、1、2、3、4、5、6、7、8、9、A(表示10)、B(表示11)、C(表示12)、D(表示13)、E(表示14)、F(表示15)。

【典例精析】【例1】把十进制数38改写成二进制数。

）（）（21010011038=【趁热打铁-1】把十进制数12改写成二进制数。

）（）（210110012=【例2】把十进制数512改成8进制数。

）（）（8101000512=【趁热打铁-2】把十进制数202改成8进制数。

）（）（810312202=【例3】把十进制数202改成16进制数。

）（）（1610202CA =【趁热打铁-3】把十进制数512改成16进制数。

）（）（1610200512=【例4】把二进制数()2110改写成十进制数。

）（）（1026110=【趁热打铁-4】把二进制数()211011改写成十进制数。

）（）（1022711011=【例5】把二进制数()2110改写成八进制数。

）（）（826110=【趁热打铁-5】把二进制数()211011改写成八进制数。

）（）（823311011=【例6】计算()()22101111+。

()()22101111+=()21110【趁热打铁-6】计算()()22101101101+。

()()22101101101+=()2110010【例7】计算()()22110111⨯。

()()22110111⨯=()2100111【趁热打铁-7】计算()()2211001101⨯。

()()2211001101⨯=()21111101【例8】计算()()221111101÷。

小学奥数教程之进制的计算 教师版 全国通用了解进制；会将十进制数转换成多进制；会将多进制转换成十进制；会多进制的混合运算；能够判定进制.一、数的进制1.十进制：我们常用的进制为十进制，特点是“逢十进一”。

在实际生活中，除了十进制计数法外，还有其他的大于1的自然数进位制。

比如二进制，八进制，十六进制等。

2.二进制：在运算机中，所采纳的计数法是二进制，即“逢二进一”。

因此，二进制中只用两个数字0和1。

二进制的计数单位分别是1、21、22、23、……，二进制数也能够写做展开式的形式，例如100110在二进制中表示为：(100110)2=1×25+0×24+0×23+1×22+1×21+0×20。

二进制的运算法则：“满二进一”、“借一当二”，乘法口诀是：零零得零，一零得零，零一得零，一一得一。

注意：关于任意自然数n,我们有n0=1。

3.k 进制：一样地，关于k 进位制，每个数是由0，1，2，，1k -（）共k 个数码组成，且“逢k 进一”．1k k >（）进位制计数单位是0k ，1k ，2k ，．如二进位制的计数单位是02，12，22，，八进位制的计数单位是08，18，28，． 4.k 进位制数能够写成不同计数单位的数之和的形式十进制表示形式：1010101010n n n n N a a a --=+++； 二进制表示形式：1010222n n n n N a a a --=+++； 知识点拨 教学目标为了区别各进位制中的数，在给出数的右下方写上k ，表示是k 进位制的数如：8352（），21010（），123145（）,分别表示八进位制，二进位制，十二进位制中的数．5.k 进制的四则混合运算和十进制一样 先乘除，后加减；同级运算，先左后右；有括号时先运算括号内的。

二、进制间的转换：一样地，十进制整数化为k 进制数的方法是：除以k 取余数，一直除到被除数小于k 为止，余数由下到上按从左到右顺序排列即为k 进制数．反过来，k 进制数化为十进制数的一样方法是：第一将k 进制数按k 的次幂形式展开，然后按十进制数相加即可得结果．如右图所示:模块一、十进制化成多进制 把9865转化成二进制、五进制、八进制，看看谁是最细心的。