滑动轴承计算
- 格式:docx
- 大小:539.09 KB
- 文档页数:23

滑动轴承间隙计算
滑动轴承的间隙计算方法可以根据轴承的类型和使用要求而有所不同。
以下是一种常见的间隙计算方法:
1. 确定滑动轴承类型:常见的滑动轴承类型有径向滑动轴承和推力滑动轴承。
根据具体的使用要求选择相应的轴承类型。
2. 确定负荷条件:根据实际应用中的负荷条件,包括径向负荷和推力负荷,确定轴承的工作负荷。
3. 计算轴承间隙:根据轴承的类型和工作负荷,使用滑动轴承间隙计算公式计算轴承的间隙。
- 对于径向滑动轴承,一般采用以下公式计算轴承间隙:间隙= ε × √(负荷/ (π × d × L × μ))
其中,ε为系数(一般为0.2-1.0),d为轴承内径,L为轴承长度,μ为润滑油的黏度。
- 对于推力滑动轴承,一般采用以下公式计算轴承间隙:间隙= ε × √(负荷/ (π × d × L × μ))
其中,ε为系数(一般为0.2-1.0),d为轴承内径,L为轴承长度,μ为润滑油的黏度。
4. 根据实际要求调整间隙:根据实际应用要求,对计算得到的间隙进行调整。
一般来说,间隙过小会导致润滑不良,间隙过大则会导致轴承的振动和松动。
需要注意的是,以上的计算方法只是一种常见的方法,实际应用中还需要考虑其他因素,如温度、工作速度等。
最好咨询专业的轴承制造商或工程师来进行具体的间隙计算。


液体动力润滑径向滑动轴承设计计算流体动力润滑的楔效应承载机理已在第四章作过简要说明,本章将讨论流体动力润滑理论的基本方程(即雷诺方程)及其在液体动力润滑径向滑动轴承设计计算中的应用。
(一)流体动力润滑的基本方程流体动力润滑理论的基本方程是流体膜压力分布的微分方程。
它是从粘性流体动力学的基本方程出发,作了一些假设条件后得出的。
假设条件:流体为牛顿流体;流体膜中流体的流动是层流;忽略压力对流体粘度的影响;略去惯性力及重力的影响;认为流体不可压缩;流体膜中的压力沿膜厚方向不变。
图12-12中,两平板被润滑油隔开,设板A 沿x 轴方向以速度v 移动;另一板B 为静止。
再假定油在两平板间沿 z 轴方向没有流动(可视此运动副在z 轴方向的尺寸为无限大)。
现从层流运动的油膜中取一微单元体进行分析。
作用在此微单元体右面和左面的压力分别为p 及p p dx x ∂⎛⎞+⎜∂⎝⎠⎟,作用在单元体上、下两面的切应力分别为τ及dy y ττ⎛⎞∂+⎜⎟∂⎝⎠。
根据x 方向的平衡条件,得:整理后得根据牛顿流体摩擦定律,得,代入上式得 该式表示了压力沿x 轴方向的变化与速度沿y 轴方向的变化关系。
下面进一步介绍流体动力润滑理论的基本方程。
1.油层的速度分布将上式改写成(a)对y 积分后得(c)根据边界条件决定积分常数C1及C2:当y=0时,v= V;y=h(h为相应于所取单元体处的油膜厚度)时,v=0,则得:代入(c)式后,即得 (d)由上可见,v由两部分组成:式中前一项表示速度呈线性分布,这是直接由剪切流引起的;后一项表示速度呈抛物线分布,这是由油流沿x方向的变化所产生的压力流所引起的。
2、润滑油流量当无侧漏时,润滑油在单位时间内流经任意截面上单位宽度面积的流量为:将式(d)代入式(e)并积分后,得(f)设在 p=p max处的油膜厚度为h0(即时当润滑油连续流动时,各截面的流量相等,由此得 :整理后得该式为一维雷诺方程。

轴承的摩擦系数
为便于与滑动轴承比较,滚动轴承的摩擦力矩可按轴承内径由下式计算:M=uPd/2
这里,
M:摩擦力矩,
u:摩擦系数,表1
P:轴承负荷,N
d:轴承公称内径,mm
摩擦系数u受轴承型式、轴承负荷、转速、润滑方式等的影响较大,一般条件下稳定旋转时的摩擦系数参考值如表1所示。
对于滑动轴承,一般u=,有时也达。
各类轴承的摩擦系数u
轴承型式摩擦系数u
深沟球轴承
角接触球轴承
调心球轴承
圆柱滚子轴承
满装型滚针轴承
带保持架滚针轴承
圆锥滚子轴承
调心滚子轴承
推力球轴承
推力调心滚子轴承由轴承摩擦引起的轴承功率损失可用以下计算公式得出
NR = 1,05 x 10-4 Mn
其中
NR = 功率损失,W
M = 轴承的总摩擦力矩,Nmm
n = 转速,r/min
电机扭矩公式:T=9550*P/n
T:电机转矩
P:电机功率KW
n:转速r/min。



滑动轴承刚度和阻尼计算的fluent udf序滑动轴承在工程领域中扮演着重要的角色,它们常常被用于支撑旋转机械设备,并承受高速旋转下的摩擦和载荷。
而对于滑动轴承的设计和优化,则需要了解其刚度和阻尼等重要参数。
本文将探讨在使用Fluent UDF进行滑动轴承刚度和阻尼计算的过程,希望能为工程师们提供一些有价值的指导。
一、滑动轴承的作用和重要性1. 滑动轴承的定义和原理在工程应用中,滑动轴承是一种通过壁压力维持摩擦阻力的设备,用于支撑和定位旋转机械部件。
其基本原理是通过摩擦力和表面压力来支撑和限制轴的运动,从而减少磨损和能量损失。
2. 滑动轴承的重要性滑动轴承作为机械设备中的关键部件,其性能对于整个机械系统的安全性和稳定性有着重要的影响。
了解滑动轴承的刚度和阻尼等参数,对于提高机械设备的运行效率和使用寿命具有重要意义。
二、使用Fluent UDF进行滑动轴承刚度和阻尼计算的步骤1. Fluent UDF的介绍Fluent UDF是用于Fluent软件的用户定义函数,它可以通过编程的方式对流体流动、传热和化学反应等进行定制化处理。
在滑动轴承的刚度和阻尼计算中,可以通过编写Fluent UDF来实现定制化的计算和分析。
2. 刚度和阻尼的定义在进行滑动轴承刚度和阻尼的计算之前,首先需要了解其定义。
滑动轴承的刚度可以理解为其在受力作用下的变形能力,而阻尼则是指其在受到外界振动或冲击时的能量消耗能力。
3. Fluent UDF的编写在使用Fluent UDF进行滑动轴承刚度和阻尼计算时,需要编写相应的函数来描述滑动轴承在不同工况下的力学特性。
这包括了材料特性、载荷情况、流体力学等方面的计算和分析。
4. 数据采集和分析通过编写好的Fluent UDF,可以对滑动轴承在不同工况下的刚度和阻尼进行计算和分析。
这需要对液压力、位移变形等参数进行实时监测和数据采集,然后进行相应的分析和处理。
三、对滑动轴承刚度和阻尼计算的个人观点和理解1. 刚度和阻尼对于滑动轴承的重要性在滑动轴承的设计和优化过程中,刚度和阻尼是需要重点考虑的参数。

动载滑动轴承轴心轨迹计算在往复式机械中,作用在连杆大小端及曲轴的滑动轴承上的载荷,无论大小和方向都随时间作周期性变化。
动载轴承由于油膜动压受旋转效应和挤压效应的综合作用,其轴心轨迹是变化的。
在正常的工况下,其轴心轨迹收敛于固定的轨迹曲线。
动载轴承的轴心轨迹的计算可以估计出轴承的失效形式及失效位置,从而在设计时可作有效的预防。
对轴心轨迹的计算,不能用稳态下的计算方法来确定,这是因为其油膜动压涉及挤压效应和旋转效应的综合作用,因而要采用非稳态下的计算方法才能确定。
本文主要采用Holland方法并通过计算机模拟进行计算。
图1 轴承模型示意图1.建立模型在进行轴心轨迹的计算之前,对有限宽的动载轴承作以下假设:(1)轴承的间隙中充满润滑油介质,流动服从雷诺方程,不考虑润滑油的涡动现象;(2)整圆轴承,轴承的轴线和轴颈平行;(3)轴承外表面光整;(4)不考虑温度场变化引起的油粘度变化。
求解轴心轨迹的基本思路如下,在油膜力和载荷互相平衡的情况下(由于轴颈惯性力相对较小,因此可以忽略不计),轴心都会逐渐收敛于一个确定的轨迹,所以可在轴颈的任意初始位置上根据力平衡关系确定轴心变化速度。
由此得到经过一微小时间间隔后的新的轴颈位置。
从这个位置再确定新的轴心变位速度,又得到另一时间间隔后的另一个轴颈位置。
如此不断进行下去,直到收敛于一个封闭的轴心轨迹。
分析动载轴承轴心轨迹的具体方法有Holland法、和Hahn法和移动率(Mobility)法。
为了克服对动载Reynolds方程在数学上求通解的困难,采用Holland法进行分析。
图1为物理模型的受力关系示意。
图中,F为动载荷,γ为动载荷与Y轴的方向角,δ为偏位角,Ωb为轴承角速度,Ωj为轴颈角速度,轴颈中心O j绕轴承中心O b的回转变位角速度为δ’,偏心率随时间的增长速率为ε’,R为轴承的内径。
P D是由轴颈和轴承相对油楔的旋转角速度引起的油膜动压,P V是由轴颈与轴承之间的挤压引起的油膜动压,称为挤压油压。
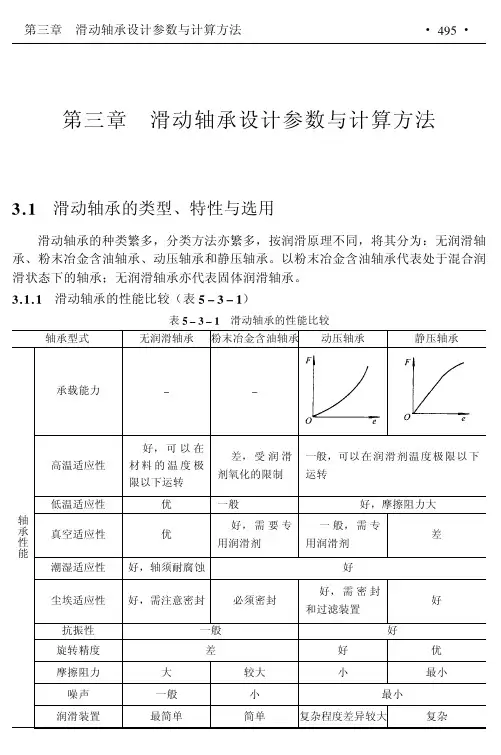
第三章滑动轴承设计参数与计算方法!"#滑动轴承的类型、特性与选用滑动轴承的种类繁多,分类方法亦繁多,按润滑原理不同,将其分为:无润滑轴承、粉末冶金含油轴承、动压轴承和静压轴承。
以粉末冶金含油轴承代表处于混合润滑状态下的轴承;无润滑轴承亦代表固体润滑轴承。
!"#"#滑动轴承的性能比较(表$%!%#)表$%!%#滑动轴承的性能比较轴承型式无润滑轴承粉末冶金含油轴承动压轴承静压轴承轴承性能承载能力!!高温适应性好,可以在材料的温度极限以下运转差,受润滑剂氧化的限制一般,可以在润滑剂温度极限以下运转低温适应性优一般好,摩擦阻力大真空适应性优好,需要专用润滑剂一般,需专用润滑剂差潮湿适应性好,轴须耐腐蚀好尘埃适应性好,需注意密封必须密封好,需密封和过滤装置好抗振性一般好旋转精度差好优摩擦阻力大较大小最小噪声一般小最小润滑装置最简单简单复杂程度差异较大复杂w w w.bz f x w.c om!"#"$滑动轴承的承载能力与极限转速几种主要滑动轴承的极限承载能力和极限转速曲线见图!"#"$和图!"#"%。
可供选择滑动轴承类型时参考。
对动压轴承,按中等粘度润滑油进行计算;对无润滑轴承和混合润滑轴承,按磨损寿命为$&’(计算;对静压轴承,理论上在材料强度允许图%&!&#径向轴承的极限载荷与转速""""无润滑轴承—·—液体动压轴承—··—粉末冶金含油轴承—滚动轴承图%&!&$推力轴承的极限载荷与转速""""无润滑轴承—·—液体动压轴承—··—粉末冶金含油轴承—滚动轴承w w w.bz f x w.c om的载荷和转速范围内均可应用。
为了便于比较,还将疲劳寿命为!"#$的滚动轴承的极限承载能力和极限转速曲线画出。


第十七章 滑动轴承基本要求及重点、难点滑动轴承的结构、类型、特点及轴瓦材料与结构。
非液体摩擦轴承的计算。
液体动压形成原理及基本方程,液体动压径向滑动轴承的计算要点。
多油楔动压轴承简介。
润滑剂与润滑装置。
基本要求:1) 了解滑动轴承的类型、特点及其应用。
2) 掌握各类滑动轴承的结构特点。
3) 了解对轴瓦材料的基本要求和常用轴瓦材料,了解轴瓦结构。
4) 掌握非液体摩擦轴承的设计计算准则及其物理意义。
5) 掌握液体动压润滑的基本概念、基本方程和油楔承载机理。
6) 了解液体摩擦动压径向润滑轴承的计算要点(工作过程、压力曲线及需要进行哪些计算)。
7) 了解多油楔轴承等其他动压轴承的工作原理、特点及应用。
8) 了解滑动轴承采用的润滑剂与润滑装置。
重点:1) 轴瓦材料及其应用。
2) 非液体摩擦滑动轴承的设计准则与方法。
3) 液体动压润滑的基本方程及形成液体动压润滑的必要条件。
难点:液体动压润滑的基本方程及形成液体动压润滑的必要条件。
主要内容:一:非液体润滑轴承的设计计算。
二:形成动压油膜的必要条件。
三:流体动压向心滑动轴承的设计计算方法,参数选择§17-1概述:滑动轴承是支撑轴承的零件或部件,轴颈与轴瓦面接触,属滑动摩擦。
一 分类:1.按承载方向 径向轴承(向心轴承。
普通轴承)只受.推力轴承: 只受 组合轴承:,.2.按润滑状态 液体润滑: 摩擦表面被一流体膜分开(1.5—2.0以上)表面间摩擦为液体分子间的摩擦 。
例如汽轮机的主轴。
非液体润滑:处于边界摩擦及混合摩擦状态下工作的轴承为非液体润滑轴承。
rF aF aF rF m关于摩擦干:不加任何润滑剂。
边界:表面被吸附的边界膜隔开,摩擦性质不取决于流体粘度,与边界膜的表面的吸附性质有关。
液体:表面被液体隔开,摩擦性质取决于流体内分子间粘性阻力。
混合:处于上述的混合状态.相应的润滑状态称边界、液体、混合、润滑。
3.液体润滑按流体膜形成原理分:1)流体动压润滑轴承:靠摩擦表面几何形状相对运动并借助粘性流体动力学作用产生力。
稳健设计理论在液体动压滑动轴承中的应用滑动轴承是各种传动装置中广泛采用的支承件,特别是在高速运转机械中,为了减小摩擦,提高传动效率,要求轴承与轴颈间脱离接触并具有足够的油膜厚度,以形成液体间的摩擦状态。
在滑动轴承设计中,只有当轴承尺寸、轴承载荷、相对运动速度、润滑油的粘度、轴承间隙以及表面粗糙度之间满足一定关系时,才能实现液体摩擦。
任一参数取值不当,将出现非液体摩擦状态,导致液体摩擦的失效。
以上参数的优化设计对轴承的使用性能及寿命有十分重要的作用。
通常,在设计中,往往对轴承的各设计参数和使用条件提出更高要求。
轴承的设计参数或误差对轴承的性能的影响是非线性的,在不同的设计方案中,同样的误差程度,所产生的性能波动不尽相同。
稳健设计就是找到一种设计方案,使得液体动压轴承的性能对误差不十分敏感,同时达到较宽松的加工经济精度而降低成本的目的。
本文对某液体动压滑动轴承进行稳健设计,建立相应的数学模型,并求得优化的设计方案。
1滑动轴承的工程分析下面是径向动压滑动轴承的一组计算公式。
1.最小油膜厚度h minh min=C-e=C(1-ε)=rψ(1-ε)(1)式中C=R-r——半径间隙,R轴承孔半径;r轴颈半径;ε=e/C——偏心率;e为偏心距;ψ=C/r——相对间隙,常取ψ=(0.6-1)×10-3(v)1/4,v 为轴颈表面的线速(m/s )设计时,最小油膜厚度h min 必须满足:h min /(R z1+R z2)≥2-3[1](2)式中R z1、R z2为轴颈和轴承的表面粗糙度。
2.轴承的特性系数(索氏系数)S=μn /(p ψ2)(3)式中μ——润滑油在轴承平均工作温度下的动力粘度(Pa ·s );n ——轴颈的转速(r/s );p ——平均压强(N/m 2)用来检验轴承能否实现液体润滑。
ε值可按下面简化式求解。
A ε2+E ε+C=0(4)其中A=2.31(B/d)-2,E=-(2.052A +1),C=1+1.052A -6.4088S.上式中d ——轴径的直径(m );B ——轴承的宽度(m )通常ε选在0.5-0.95之间,超出0-1间的值,均非ε的解[1]。
第十七章滑动轴承基本要求及重点、难点滑动轴承的结构、类型、特点及轴瓦材料与结构。
非液体摩擦轴承的计算。
液体动压形成原理及基本方程,液体动压径向滑动轴承的计算要点。
多油楔动压轴承简介。
润滑剂与润滑装置。
基本要求:1) 了解滑动轴承的类型、特点及其应用。
2) 掌握各类滑动轴承的结构特点。
3) 了解对轴瓦材料的基本要求和常用轴瓦材料,了解轴瓦结构。
4) 掌握非液体摩擦轴承的设计计算准则及其物理意义。
5) 掌握液体动压润滑的基本概念、基本方程和油楔承载机理。
6) 了解液体摩擦动压径向润滑轴承的计算要点(工作过程、压力曲线及需要进行哪些计算)。
7) 了解多油楔轴承等其他动压轴承的工作原理、特点及应用。
8) 了解滑动轴承采用的润滑剂与润滑装置。
重点:1) 轴瓦材料及其应用。
2) 非液体摩擦滑动轴承的设计准则与方法。
3) 液体动压润滑的基本方程及形成液体动压润滑的必要条件。
难点:液体动压润滑的基本方程及形成液体动压润滑的必要条件。
主要内容:一:非液体润滑轴承的设计计算。
二:形成动压油膜的必要条件。
三:流体动压向心滑动轴承的设计计算方法,参数选择§17-1概述:滑动轴承是支撑轴承的零件或部件,轴颈与轴瓦面接触,属滑动摩擦。
一 分类:1. 按承载方向 径向轴承(向心轴承。
普通轴承)只受.推力轴承: 只受组合轴承:,. 2. 按润滑状态 液体润滑: 摩擦表面被一流体膜分开(1.5—2.0以上)表面间摩擦为液体分子间的摩擦 。
例如汽轮机的主轴。
非液体润滑:处于边界摩擦及混合摩擦状态下工作的轴承为非液体润滑轴承。
关于摩擦 干: 不加任何润滑剂。
边界:表面被吸附的边界膜隔开,摩擦性质不取决于流体粘度,与边界膜的表面的吸附性质有关。
液体:表面被液体隔开,摩擦性质取决于流体内分子间粘性阻力。
混合:处于上述的混合状态.相应的润滑状态称边界、液体、混合、 润滑。
r F a F a F r F m3.液体润滑按流体膜形成原理分:1)流体动压润滑轴承:靠摩擦表面几何形状相对运动并借助粘性流体动力学作用产生力。
平衡外载。
2)流体静压润滑轴承:靠外部提供压力流体,借助流体静压力平衡外载荷。
但开始启动时处于干摩擦,逐渐转换的,表明滑动轴承摩擦状态转化过程滑动轴承摩擦特性曲线。
由德国科学家Stribeck通过实验做出的。
3.按润滑材料分液体润滑轴承(油、水)气体润滑轴承(空气、氦、氮)塑料体润滑轴承(脂、半夜体金属、、) 固体润滑轴承 (、、石墨,玻璃)自润滑轴承(粉末冶金)二 :主要特点:1.平稳, 可靠, 噪音小,高旋转精度2.承载力大,耐冲击(油膜缓冲阻尼作用),用于高速3.启动阻力大。
§17--2 径向滑动轴承的主要类型整体式:结构简单,低速、载荷不大 , 间歇机器无法调间隙,轴颈只能从端部装入。
剖分式 : 见教材P334图17.1-17.2。
§17—3滑动轴承材料:即轴瓦与轴承衬材料。
一:对材料要求:1. 强度塑性 顺应性 嵌藏性2. 磨合性减摩性 耐磨性磨合性 材料消除表面不平度而使轴瓦表面和轴颈表面相互吻合的性质减摩性:材料具有较低摩擦阻力的性质。
耐磨性:材料具有抵抗磨粒磨损和胶合磨损的性质。
3.良好的导热性、工艺性 、经济性。
b P n S n I b P n S s m v /30二:常用材料:1. 材料分类:金属材料粉末冶金材料非金属材料2. 常用材料简介:1) 巴氏合金(轴承合金)、、、合金 ,以、为基础,悬浮锑锡及铜锡的硬晶粒,均匀的分布于基体内,硬晶粒起抗磨作用软基体则增加材料的塑性。
2)轴承青铜:粉末冶金:金属粉末加石墨高压成型再经高温烧制而成的多空隙结构材料。
孔隙率占总体积的15-35%,可预先浸满油或脂,又称含油轴承。
3)塑料:耐水耐酸耐碱,但导热性差耐塑性差。
详见p355表17.1§17—7 滑动轴承的条件性计算用于低速轻载不重要轴承,也用于流体润滑的初算。
非液体润滑轴承计算缺乏系统理论,用一些条件性的验算来进行计算。
失效形式:磨损(主要)无合适公式胶合(次要)点蚀(更次要)一、径向轴承。
1. 限制平均压强P 即限制磨损失效。
u C n S b P b S n S b P 110P ZCuSn(17.2)F------ 轴承径向载荷----轴颈直径及有效宽mm----许用比压Mpa 表17.4 P342 2.限制值即限制胶合因发热量有摩擦功率损失而来,与功率损失成正比,因而限制值就可以限制发热量,进而限制了胶合。
发热量式中f —摩擦系数; F —力(); —速度上式中B 、d 一定,f 一定,为变值、可控制此项即可限制胶合失效。
(17-3)3.限制滑动速度:有时由于安装误差或轴的弹性变形,使轴径与轴承局部接触,此时即使平均比压较小,及皆小于许用值,但也可能由于轴颈圆周速度较高,而使轴承局部过度磨损或胶合。
因此安装精度较差、轴的弹性变形较大和轴承宽径比较大时,还需验算轴径的圆周速度。
(17-4)材料的pv 及v 见教材表17.4[]P B d F P ≤⋅=N dB []P pv pv pv v p d B f s m v F f H ⋅⋅⋅⋅=⋅⋅=)/(N v pv []s m Mp pv B n F dn Bd F pv a /2000100060⋅≤⋅⋅=⨯⋅=πv p p pv v []s m v dnv /100060≤⨯=π二、推力轴承(见教材P342页,略)§17—8液体动压润滑的基本方程用润滑油把摩擦表面完全分割开的摩擦成为液体摩擦,此时摩擦性质取决于润获的黏度,而与两摩擦表面间的材料无关。
一:润滑油粘度1.润滑油在运动过程中产生内部摩擦阻力的性质叫粘性,粘性大小称粘度。
粘度是表征流体流动中内摩擦性能的。
2.内摩擦阻力的计算:图是为两块平行平板被一层不可压缩的润滑油隔开,下板静止加压力拖动上板,润滑油做层流流动。
沿y 坐标轴油层将以不同速度u 在移动。
流动时内摩擦阻力阻止层流流动,此力称流体内摩擦阻力。
关于内摩擦阻力的大小:速度位置速度梯度,即速度在垂直方向上的变化率。
由理论分析及试验结果剪应力与速度梯度成正比。
因方向取负,负号表示随的增大而减小,当温度、压力一定时,为一常数称为动力粘度。
上述方程称牛顿方程或流体内摩擦定律2. 粘度单位τv τy u ∂∂∝τy u ∂∂=ητy u y η1) 动力粘度(绝对粘度):单位为动力学单位,称动力粘度。
国际单位(工程单位):巴斯()长宽高各为1m 的液体如使两平行面a .b 发生1m/s 相对滑动速度所需的力为1N.这样的液体粘度为物理单位 泊或2) 运动粘度动力粘度与同温度下该液体的密度的比值称运动粘度。
国际单位:物理单位:斯(Stock ),蒸馏水在20.3摄氏度时运动粘度为1新标准规定机械油牌号为40摄氏度时运动粘度的厘斯数,温度上升,粘度下降;压力升高,粘度上升,超过100Mpa 时压力升高,粘度明显增加。
二:流体动压润滑的形成(润滑油是怎样起作用的,压力如何产生的)s Pa ⋅2/1m s N ⋅)(poise P s Pa cP P cm s dyn ⋅===⋅1.0(1001/12厘泊)cP P s Pa 1000101==⋅s m m Kg m ss m Kg m Kg m s N s m /)/(/(2322322=⋅⋅=⋅==ρηγcSt s cm cm g s s cm g cm g cm s dyn St 100/1/)/(/1/123222==⋅⋅=⋅==ρηcSt(a)如图17.14.b所示:板b静止,板a以速度v向右移动,板上无载荷,液体速度图呈三角形分布,板ab间带进油量等于带出油量,板间油量保持不变,板a不会下沉。
(b)板a承载,油向两侧溢出,于是板a下沉,不能承载。
(c)如图17.14 a所示,ab板不平行,板间隙沿运动方向由大到小呈收敛的楔形,板a 承受载荷P。
板a运动使两端流体速度图似乎应如虚线所示的三角形分布。
如此进油多出油少,由于实际上液体不可压缩,必将在间隙内拥挤形成压力,迫使进口端的速度图向内凹,出口端速度图形向外凸,使进口油量等与出口带出的油量。
间隙内液体形成压力,即由向上的压力与外载荷平衡,说明在间隙内形成了动压油膜。
归纳起来:获得流体动压润滑的必要条件是:1)相对运动两表面间,必须有沿运动方向由大变小的楔形间隙;2)两表面必须有一定的相对速度3)润滑油有一定粘度,且供油充足。
进一步观察径向轴承形成动压油膜的过程:(1)如图17.16 a所示,制造时轴承孔直径D大于轴径d,二者之差称直径间隙。
静止时轴处于轴承孔最下方稳定位置。
(2)轴径开始转动时,轴承与轴径为金属相接触,为金属间直接相摩擦。
轴承对轴径的摩擦力方向与轴径表面圆周速度方向相反,迫使轴径向左移动而偏移。
如图17.16 b 所示(3)当轴径速度继续增加时,楔形间隙内形成的油膜将轴径推开而与轴承脱离接触,但此情况不持久,因为油膜内各点内压力的合力有向右推动轴径的分力存在,因而轴径向右移动。
(4)随转速的增大,轴径表面圆周速度增大,带入油楔内油量逐渐加多,则金属接触面被润滑油分隔开的面积增大,因而摩擦阻力下降。
于是轴径又向右下方移动(油膜内各点压力的合力有向右推动轴径的分力存在)。
当转速增加到一定大小达到工作转速时,已形成足够油量将金属接触面分开,轴承开始按液体摩擦状态工作。
油压如何计算?通过雷诺方程解决。
三:流体动压润滑的基本方程------雷诺方程如图17.13所示两刚体被润滑油分开,移动件以速度v沿x方向移动,另一刚体静止不动。
假设:1. z 方向无穷大,(润滑油在此方向不流动);2. 润滑油做层流流动,油不可压缩;3. 润滑油粘度不随温度压力变化;4. 忽略油层重力和惯性;5. 由于工作表面吸附牢固,表面油分子随工作表面一同运动或静止。
取单元微体分析,p 为单位压力。
因沿z 方向不流动,因而前后面压强相等。
作用于微元体两侧压力及作用于微元体上下两面压力为及分析x 方向受力,因为等速运动,所以受力平衡:dz pdy ⋅dz dy dx x pp ⋅∂∂+)(dz dx ⋅⋅τdz dx dy dy dp⋅+)(τ∑=0x 0)()(=⋅∂∂+-⋅⋅+⋅∂∂+-⋅⋅dz dx dy ydz dx dz dy dx x p p dz dy p τττ代入牛顿定律得:得 反过来分析一下平行板的情况:如图,速度分布为三角形 ,即不能产生压力来支撑外载荷(平行油膜各处油压差等于入口及出口的油压)。
上式积分:再积分:利用边界条件,当y=0时(移动件)得=当时(静止件)得导出:将、代入原式得0=∂∂-∂∂-dydxdz y dxdydz x p τy x p ∂∂-=∂∂∴τy u∂∂=ητ22y u xp ∂∂=∂∂η常数=∂∂∴y u0022=∂∂∴=∂∂x pyu ∴111C y dx dp dy x l y u +=∂∂=∂∂⎰ηη212121)1(C y C y x p dy C y x p u ++∂∂=+∂∂=⎰ηηv u =2C v h y =0=u h vh x p C -∂∂-=211ηhv h dx dp h vh x p C vh C h x p u C y C y x p u --=-∂∂-=∴++∂∂=∴++⋅∂∂=212121212112212ηηηη1C 2C利用润滑油连续流动的关系得出任一剖面沿x 方向单位宽度流量:[导出:=u (速度)x 截面积=dz=udy (因为单位宽,所以dz=1)==Vh(a )设以表示油膜中油压最大处的间隙(=0)此截面上(b )而式(a )应等于式(b ) (因为流量必相等)== (7—7))(21)()21(21)21)1(22121h y y xpy h h v v y h vy h x p y x p C y C y x p dy C y x p u -∂∂+-=+-∂∂-⋅∂∂=++⋅∂∂=+⋅∂∂=⎰ηηηηη⎰=hx udyq 0xq udy ⎰-∂∂+-hdy h y y x p y h h V 0)](21)([η2213212232h h x p h x p h h V ∂∂-∂∂+-ηη31212h x p V ∂∂-=ηη0hx p ∂∂=x q 021vh ∴31212h x P V ∂∂-ηη021vh ∴x P ∂∂30003230)(62166121212h h h vvh h h v h v hvh vh -==-=-ηηηη此为一维雷诺流体动压润滑方程,是计算流体动压润滑的基本方程,从公式可看出油压变化与粘度、速度、间隙有关,利用此公式可求出油膜上各点压力P ,根据油压分布可算出油膜承载能力。