下载文档原格式
二十二章滑动轴承习题与参考答案一、选择题(从给出的A 、B 、C 、D 中选一个答案)1 验算滑动轴承最小油膜厚度h min 的目的是 。
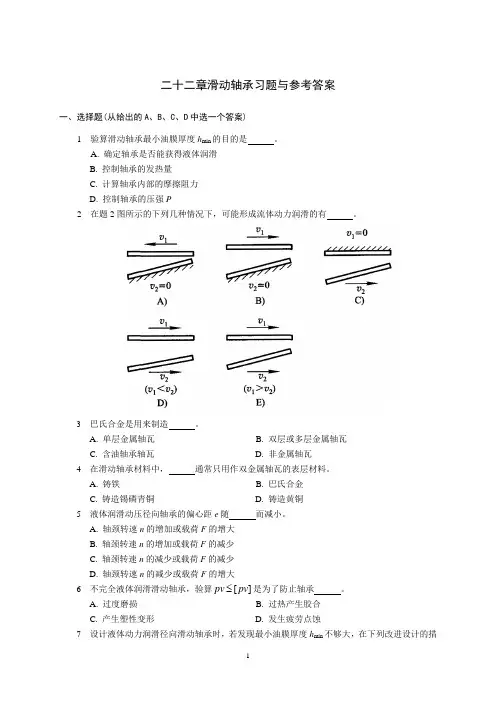
A. 确定轴承是否能获得液体润滑B. 控制轴承的发热量C. 计算轴承内部的摩擦阻力D. 控制轴承的压强P2 在题2图所示的下列几种情况下，可能形成流体动力润滑的有 。
3 巴氏合金是用来制造 。
A. 单层金属轴瓦B. 双层或多层金属轴瓦C. 含油轴承轴瓦D. 非金属轴瓦 4 在滑动轴承材料中， 通常只用作双金属轴瓦的表层材料。
A. 铸铁 B. 巴氏合金 C. 铸造锡磷青铜 D. 铸造黄铜 5 液体润滑动压径向轴承的偏心距e 随 而减小。
A. 轴颈转速n 的增加或载荷F 的增大 B. 轴颈转速n 的增加或载荷F 的减少 C. 轴颈转速n 的减少或载荷F 的减少 D. 轴颈转速n 的减少或载荷F 的增大6 不完全液体润滑滑动轴承，验算][pv pv 是为了防止轴承 。
A. 过度磨损 B. 过热产生胶合 C. 产生塑性变形 D. 发生疲劳点蚀7 设计液体动力润滑径向滑动轴承时，若发现最小油膜厚度h min 不够大，在下列改进设计的措施中，最有效的是 。
A. 减少轴承的宽径比d l /B. 增加供油量C. 减少相对间隙ψD. 增大偏心率χ 8 在 情况下，滑动轴承润滑油的粘度不应选得较高。
A. 重载 B. 高速C. 工作温度高D. 承受变载荷或振动冲击载荷 9 温度升高时，润滑油的粘度 。
A. 随之升高B. 保持不变C. 随之降低D. 可能升高也可能降低 10 动压润滑滑动轴承能建立油压的条件中，不必要的条件是 。
A. 轴颈和轴承间构成楔形间隙 B. 充分供应润滑油C. 轴颈和轴承表面之间有相对滑动D. 润滑油温度不超过50℃11 运动粘度是动力粘度与同温度下润滑油 的比值。
A. 质量B. 密度C. 比重D. 流速 12 润滑油的 ，又称绝对粘度。
A. 运动粘度B. 动力粘度C. 恩格尔粘度D. 基本粘度 13 下列各种机械设备中， 只宜采用滑动轴承。
滑动轴承一、摩擦状态；二、轴瓦及轴承衬材料；三、非液体摩擦滑动轴承的计算；四、液体动压润滑径向滑动轴承设计计算。
１．（华东理工大学２００４年考研试题）下述材料中，巴氏合金是（ ）。
Ａ．２０ＣｒＭｎＴｉＢ．ＺＣｈＰｂＳｂＣ．ＧＣｒ１５Ｄ．３８ＳｉＭｎＭｏ２．（北京航空航天大学２００１年考研试题）非液体润滑滑动轴承的条件性设计计算中，一般进行、、的校核计算，分别为了限制、、。
３．（大连理工大学２００５年考研试题）判断题：液体动压轴承和液体静压轴承都必须用油泵供给压力油以支撑外载并润滑轴承。
４．（大连理工大学２００３年考研试题）判断题。
（１）采用多油楔轴承可以提高轴承的稳定性，而不能提高轴承承载能力。
（２）滑动轴承设计中选用较大的宽径比Ｂ／ｄ和较小的相对间隙ψ可以提高承载能力。
５．（大连理工大学２００３年考研试题）在图所示的楔润滑间隙中，润滑油在进、出口的速度应为图中（ ）所示。
６．（大连理工大学２０１１年考研试题）设计动压向心滑动轴承时，若通过热平衡计算，发现轴承温升过高，在下列改进设计的措施中，有效的是（ ）Ａ．增大轴承的宽径比Ｂ／ｄＢ．减少供油量Ｃ．增大相对间隙ψＤ．换用粘度较高的油７．（上海大学２００５年考研试题）通过直接求解雷诺方程，可以求出轴承间隙中润滑油的（ ）。
Ａ．油量分布Ｂ．压力分布Ｃ．流速分布Ｄ．温度分布８．（上海大学２００５年考研试题）一滑动轴承，已知其直径间隙Δ＝０．０８ｍｍ，现测得它的最小油膜厚度ｈｍｉｎ＝２１μｍ，轴承的偏心率χ应该是（ ）。
Ａ．０．２６Ｂ．０．４８Ｃ．０．５２Ｄ．０．７４９．（中南大学２００５年考研试题）一滑动轴承公称直径ｄ＝８０ｍｍ，相对间隙ψ＝０．００２，已知该轴承在液体摩擦状态下工作，偏心率χ＝０．４８，则最小油膜厚度ｈｍｉｎ＝（ ）。
Ａ．８４μｍＢ．４２μｍＣ．７６μｍＤ．３８μｍ１０．（中南大学２００５年考研试题）判断题：液体动力润滑径向滑动轴承中的最小油膜厚度，位于载荷作用线上。
习题与参考答案一、选择题(从给出的A 、B 、C 、D 中选一个答案)1 验算滑动轴承最小油膜厚度h min 的目的是 A 。
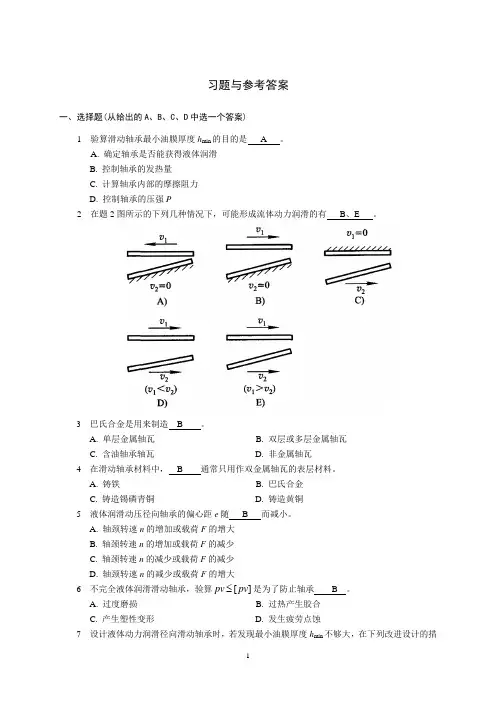
A. 确定轴承是否能获得液体润滑B. 控制轴承的发热量C. 计算轴承内部的摩擦阻力D. 控制轴承的压强P2 在题2图所示的下列几种情况下，可能形成流体动力润滑的有 B 、E 。
3 巴氏合金是用来制造 B 。
A. 单层金属轴瓦B. 双层或多层金属轴瓦C. 含油轴承轴瓦D. 非金属轴瓦 4 在滑动轴承材料中， B 通常只用作双金属轴瓦的表层材料。
A. 铸铁 B. 巴氏合金 C. 铸造锡磷青铜 D. 铸造黄铜 5 液体润滑动压径向轴承的偏心距e 随 B 而减小。
A. 轴颈转速n 的增加或载荷F 的增大 B. 轴颈转速n 的增加或载荷F 的减少 C. 轴颈转速n 的减少或载荷F 的减少 D. 轴颈转速n 的减少或载荷F 的增大6 不完全液体润滑滑动轴承，验算][pv pv 是为了防止轴承 B 。
A. 过度磨损 B. 过热产生胶合 C. 产生塑性变形 D. 发生疲劳点蚀7 设计液体动力润滑径向滑动轴承时，若发现最小油膜厚度h min 不够大，在下列改进设计的措施中，最有效的是 A 。
A. 减少轴承的宽径比d l /B. 增加供油量C. 减少相对间隙ψD. 增大偏心率χ 8 在 B 情况下，滑动轴承润滑油的粘度不应选得较高。
A. 重载 B. 高速C. 工作温度高D. 承受变载荷或振动冲击载荷 9 温度升高时，润滑油的粘度 C 。
A. 随之升高B. 保持不变C. 随之降低D. 可能升高也可能降低 10 动压润滑滑动轴承能建立油压的条件中，不必要的条件是 D 。
A. 轴颈和轴承间构成楔形间隙 B. 充分供应润滑油C. 轴颈和轴承表面之间有相对滑动D. 润滑油温度不超过50℃11 运动粘度是动力粘度与同温度下润滑油 B 的比值。
A. 质量B. 密度C. 比重D. 流速 12 润滑油的 B ，又称绝对粘度。
第十七章 滑动轴承基本要求及重点、难点滑动轴承的结构、类型、特点及轴瓦材料与结构。
非液体摩擦轴承的计算。
液体动压形成原理及基本方程，液体动压径向滑动轴承的计算要点。
多油楔动压轴承简介。
润滑剂与润滑装置。
基本要求:1) 了解滑动轴承的类型、特点及其应用。
2) 掌握各类滑动轴承的结构特点。
3) 了解对轴瓦材料的基本要求和常用轴瓦材料，了解轴瓦结构。
4) 掌握非液体摩擦轴承的设计计算准则及其物理意义。
5) 掌握液体动压润滑的基本概念、基本方程和油楔承载机理。
6) 了解液体摩擦动压径向润滑轴承的计算要点（工作过程、压力曲线及需要进行哪些计算）。
7) 了解多油楔轴承等其他动压轴承的工作原理、特点及应用。
8) 了解滑动轴承采用的润滑剂与润滑装置。
重点：1) 轴瓦材料及其应用。
2) 非液体摩擦滑动轴承的设计准则与方法。
3) 液体动压润滑的基本方程及形成液体动压润滑的必要条件。
难点：液体动压润滑的基本方程及形成液体动压润滑的必要条件。
主要内容：一：非液体润滑轴承的设计计算。
二：形成动压油膜的必要条件。
三：流体动压向心滑动轴承的设计计算方法，参数选择§17-1概述：滑动轴承是支撑轴承的零件或部件，轴颈与轴瓦面接触，属滑动摩擦。
一 分类：1.按承载方向 径向轴承（向心轴承。
普通轴承）只受.推力轴承： 只受 组合轴承：,.2.按润滑状态 液体润滑： 摩擦表面被一流体膜分开（1.5—2.0以上）表面间摩擦为液体分子间的摩擦 。
例如汽轮机的主轴。
非液体润滑：处于边界摩擦及混合摩擦状态下工作的轴承为非液体润滑轴承。
rF aF aF rF m关于摩擦干：不加任何润滑剂。
边界：表面被吸附的边界膜隔开，摩擦性质不取决于流体粘度，与边界膜的表面的吸附性质有关。
液体：表面被液体隔开,摩擦性质取决于流体内分子间粘性阻力。
混合：处于上述的混合状态.相应的润滑状态称边界、液体、混合、润滑。
3.液体润滑按流体膜形成原理分：1）流体动压润滑轴承：靠摩擦表面几何形状相对运动并借助粘性流体动力学作用产生力。
习题与参考答案一、复习思考题1 设计液体动力润滑滑动轴承时，为保证轴承正常工作，应满足哪些条件？2 试述径向动压滑动轴承油膜的形成过程。
3 就液体动力润滑的一维雷诺方程30)(6h h h v x p-=∂∂η，说明形成液体动力润滑的必要条件。
4 液体动力润滑滑动轴承的相对间隙ψ的大小，对滑动轴承的承载能力、温升和运转精度有何影响？5 有一液体动力润滑单油楔滑动轴承、在两种外载荷下工作时，其偏心率分别为6.01=χ、8.02=χ，试分析哪种情况下轴承承受的外载荷大。
为提高该轴承的承载能力，有哪些措施可供考虑？(假定轴颈直径和转速不允许改变。
)6 不完全液体润滑滑动轴承需进行哪些计算？各有何含义？7 为了保证滑动轴承获得较高的承载能力，油沟应做在什么位置？8 何谓轴承承载量系数C p ？C p 值大是否说明轴承所能承受的载荷也越大？9 滑动轴承的摩擦状态有哪几种？它们的主要区别如何？ 10 滑动轴承的主要失效形式有哪些？11 相对间隙ψ对轴承承载能力有何影响？在设计时，若算出的h min 过小或温升过高时，应如何调整ψ值？12 在设计液体动力润滑径向滑动轴承时，在其最小油膜厚度h min 不够可靠的情况下，如何调整参数来进行设计？二、选择题(从给出的A 、B 、C 、D 中选一个答案)1 验算滑动轴承最小油膜厚度h min 的目的是 。
A. 确定轴承是否能获得液体润滑B. 控制轴承的发热量C. 计算轴承内部的摩擦阻力D. 控制轴承的压强P2 在题2图所示的几种情况下，可能形成流体动力润滑的有 。
3 巴氏合金是用来制造 。
A. 单层金属轴瓦B. 双层或多层金属轴瓦C. 含油轴承轴瓦D. 非金属轴瓦 4 在滑动轴承材料中， 通常只用作双金属轴瓦的表层材料。
A. 铸铁 B. 巴氏合金 C. 铸造锡磷青铜 D. 铸造黄铜 5 液体润滑动压径向轴承的偏心距e 随 而减小。
A. 轴颈转速n 的增加或载荷F 的增大 B. 轴颈转速n 的增加或载荷F 的减少 C. 轴颈转速n 的减少或载荷F 的减少 D. 轴颈转速n 的减少或载荷F 的增大6 不完全液体润滑滑动轴承，验算][pv pv ≤是为了防止轴承 。
本科毕业设计题目流体动压润滑条件下滑动轴承的优化分析专业汽车服务工程作者姓名李洋洋学号2011206004单位机械与汽车工程学院指导教师杜娟2015年5月教务处编原创性声明本人郑重声明：所提交的学位论文是本人在导师指导下，独立进行研究取得的成果。
除文中已经引用的内容外，论文中不包含其他人已经发表或撰写过的研究成果，也不包含为获得聊城大学或其他教育机构的学位证书而使用过的材料。
对本文的研究作出重要贡献的个人和集体，均在文中以明确的方式表明。
本人承担本声明的相应责任。
学位论文作者签名：日期：指导教师签名:日期：摘要就当今的汽车而言，大约有80%的机械部件的损坏来自于磨损。
机械系统中摩擦能够得到相关的优化，更能够提高机械性能，延长其使用寿命。
然而传统发动机滑动轴承用非定常流体设计，对于发动机滑动轴承耐磨性能并没有真正的进行定性分析，缺乏一定的说服力。
本文首先介绍了滑动轴承的相关知识，然后对流体动压润滑进行详细说明并建立了流体动压润滑的计算模型，然后以发动机主轴承为例，分析轴承在不同转速下的最小油膜厚度、润滑油温升，发现转速过高时，油膜厚度过小且温升过高，导致滑动轴承不能处于良好的润滑状态，分析该现象的原因并提出相关改进方案：增粗轴颈、加宽轴承。
然后分别根据两种改进方案在不同转速下的最小油膜厚度、润滑油温升两个角度分析改进措施的优劣性。
关键词：流体动力润滑；转速；最小油膜厚度；温升AbstractIn terms of today's cars, and about 80% of the damage of the mechanical components from wear and tear. Mechanical friction in the system can get related optimization, more can improve the mechanical properties, extend its service life. However, the traditional engine bearing design with unsteady flow for engine bearing wear resistance and no real qualitative analysis, the lack of certain powers of persuasion.This paper first introduces the sliding bearing of the related knowledge, and elaborate on the hydrodynamic pressure lubrication and the calculation of hydrodynamic pressure lubrication model is established, and then to launch a main bearing as an example, analysis of the bearing under different rotational speed, the minimum oil film thickness, oil temperature rise, found at high speed, the temperature rise of the oil film thickness is too small and too high, lead to sliding bearing can't in good lubrication condition, analyses the reason of this phenomenon and put forward relevant improvement plan: enlargement of journal, widen the bearing. Then respectively according to the two kinds of improved scheme under different rotational speed, the minimum oil film thickness, oil temperature rise two Angle analysis of superiority and inferiority of some improvement measures.Keywords:hydrodynamic lubrication; Speed; Minimum oil film thickness; Temperature rise目录前言................................................................................................I I 1.轴承设计计算所涉及到的基础知识 .. (1)1.1 滑动轴承 (1)1.2牛顿粘性定律 (2)1.3.表面粗糙度 (3)1.3.1表面粗糙度定义 (3)1.3.2 表面粗糙度对零件的影响 (3)2.流体动压润滑 (4)2.1流体动压润滑基本理论 (4)2.2流体动力润滑的基本方程 (5)2.2.1油层速度的分布 (5)2.2.2润滑油流量 (6)3.发动机滑动轴承的流体润滑设计 (8)3.1建立弹性流体动压润滑的计算模型 (8)3.1.1建立动压润滑模型 (8)3.1.2相关参数选择 (8)3.2动压润滑设计 (9)3.2.1油膜承载能力的计算 (9)3.2.2最小油膜厚度的计算 (10)3.2.3轴承热平衡计算 (11)4.发动机主轴承流体润滑计算与结果分析 (12)4.1流体润滑计算 (12)4.2流体润滑计算结果分析 (15)5.发动机主轴承耐磨性改进方案 (16)5.1增大轴颈直径 (16)5.1.1最小油膜厚度分析改进方案 (16)5.1.2润滑油温升分析改进方案 (17)5.2增大轴承宽度 (17)5.2.1最小油膜厚度分析改进方案 (17)5.2.2润滑油温升分析改进方案 (18)结论 (19)参考文献 (20)致谢 (21)流体动压润滑条件下滑动轴承的耐磨性优化分析前言滑动轴承是机械系统中常见的装置之一，也是生产过程中不可或缺的原件。
液体动力润滑径向滑动轴承设计计算流体动力润滑的楔效应承载机理已在第四章作过简要说明，本章将讨论流体动力润滑理论的基本方程（即雷诺方程）及其在液体动力润滑径向滑动轴承设计计算中的应用。
（一）流体动力润滑的基本方程流体动力润滑理论的基本方程是流体膜压力分布的微分方程。
它是从粘性流体动力学的基本方程出发，作了一些假设条件后得出的。
假设条件：流体为牛顿流体；流体膜中流体的流动是层流；忽略压力对流体粘度的影响；略去惯性力及重力的影响；认为流体不可压缩；流体膜中的压力沿膜厚方向不变。
图12－12中，两平板被润滑油隔开，设板A 沿x 轴方向以速度v 移动；另一板B 为静止。
再假定油在两平板间沿 z 轴方向没有流动(可视此运动副在z 轴方向的尺寸为无限大)。
现从层流运动的油膜中取一微单元体进行分析。
作用在此微单元体右面和左面的压力分别为p 及p p dx x ∂⎛⎞+⎜∂⎝⎠⎟，作用在单元体上、下两面的切应力分别为τ及dy y ττ⎛⎞∂+⎜⎟∂⎝⎠。
根据x 方向的平衡条件,得：整理后得根据牛顿流体摩擦定律,得，代入上式得 该式表示了压力沿x 轴方向的变化与速度沿y 轴方向的变化关系。
下面进一步介绍流体动力润滑理论的基本方程。
1．油层的速度分布将上式改写成（a）对y 积分后得（c）根据边界条件决定积分常数C1及C2:当y=0时,v= V；y=h(h为相应于所取单元体处的油膜厚度)时,v=0,则得：代入（c）式后,即得 （d）由上可见,v由两部分组成：式中前一项表示速度呈线性分布，这是直接由剪切流引起的；后一项表示速度呈抛物线分布，这是由油流沿x方向的变化所产生的压力流所引起的。
2、润滑油流量当无侧漏时,润滑油在单位时间内流经任意截面上单位宽度面积的流量为：将式(d)代入式(e)并积分后,得（f）设在 p=p max处的油膜厚度为h0(即时当润滑油连续流动时,各截面的流量相等,由此得 ：整理后得该式为一维雷诺方程。
它是计算流体动力润滑滑动轴承(简称流体动压轴承)的基本方程。
可以看出,油膜压力的变化与润滑油的粘度、表面滑动速度和油膜厚度及其变化有关。
经积分后可求出油膜的承载能力。
由雷诺方程及图示的压力分布也可以看出,在h>h0段,速度分布曲线呈凹形，，即压力沿x方向逐渐增大；而在h<h0段，速度分布曲线呈凸形，，压，其由上可知,形成流体动力润滑(即形成动力油膜)的必要条件是：1.相对运动的两表面间必须形成收敛的楔形间隙。
2.被油膜分开的两表面必须有一定的相对滑动速度，运动方向为使油从大口流进,小口流出。
3.润滑油必须有一定的粘度，供油要充分。
(二)径向滑动轴承形成流体动力润滑的过程径向滑动轴承的轴颈与轴孔间必须留有间隙，如图12－13a 所示，当轴颈静止时，轴颈处于轴承孔的最低位置，并与轴瓦接触。
此时，两表面间自然形成一收敛的楔形空间。
当轴颈开始转动时，速度极低，带入轴承间隙中的油量较少，这时轴瓦对轴颈摩擦力的方向与轴颈表面圆周速度方向相反，迫使轴颈在摩擦力作用下沿孔壁向右爬升(图b)。
随着转速的增大，轴颈表面的圆周速度增大，带入楔形空间的油量也逐渐加多。
这时，右侧楔形油膜产生了一定的动压力，将轴颈向左浮起。
当轴颈达到稳定运转时，轴颈便稳定在一定的偏心位置上(图c)。
这时，轴承处于流体动力润滑状态，油膜产生的动压力与外载荷F相平衡。
此时，由于轴承内的摩擦阻力仅为液体的内阻力，故摩擦系数达到最小值。
(三)径向滑动轴承的几何关系和承载量系数图12-14为轴承工作时轴颈的位置。
如图所示，轴承和轴颈的连心线OO1与外载荷F （载荷作用在轴颈中心上）的方向形成一偏位角。
轴△=D-d （12－9） 半径间隙为轴承孔半径R与轴颈半径r之差，则δ=R-r= Δ/2 （12－10）直径间隙与轴颈公称直径之比称为相对间隙，以ψ表示，则ψ=Δ/d= δ/r （12－11）轴颈在稳定运转时，其中心O与轴承中心O1的距离，称为偏心距，用e表示。
偏心距与半径间隙的比值，称为偏心率，以χ表示，则χ=e/δ于是由图可见，最小油膜厚度为h min=δ-e=δ(1-χ)=rψ(1-χ) （12－12）对于径向滑动轴承，采用极坐标描述比较方便。
取轴颈中心O为极点，连心线OO1为极轴，对应于任意角（包括均由解上式得：若略去,并（12－13）在压力最大处的油膜厚度为：式中为相将雷诺方程写成极坐标形式,即及h,h0 代入雷诺方程后得极坐标形式的雷诺方程(12-15)将上式从油膜起始角到任进行积分，得任意位置的压力，即(12-16) 压力在外载荷方向上的分量为 ：(12-17) 把上式在到的区为了求出油膜的承载能力，理论上只需将p y乘以轴承宽度B即可。
但在实际轴承中，由于油可能从轴承的两个端面流出，故必须考虑端泄的影响。
这时，压力沿轴承宽度的变化成抛物线分布，而且其油膜压力也比无限宽轴承的压力低(图12－15)，所以乘以系数，的值取决与宽度比B/d和偏心率的大小。
这样，在角和距轴承中线为z处的油膜压力的数学表达式为(12-19)因此,对有限长轴承的总承载能力为由上式得式中于是得式中C p为一个无量纲的量，称为承载量系数，η为润滑油在轴承平均工作温度下的动力粘度，Pa·s；B为轴承宽度，m；F为外载荷，N；V为轴颈圆周速度，m/s。
C p的积分非常困难，因而采用数值积分的方法进行计算，并作成相应的线图或表格供设计应用。
在给定边界条件时，C p是轴颈在轴承中位置的函数，其值取决于轴承的包角α(入油口和出油口所包轴颈的夹角)，相对偏心率和宽径比B/d。
当轴承的包角α(α=120°，180°或360°）给定时，经过一系列的换算，C p可表示为：若轴承是在非承载区内进行无压力供油,且设液体动压力是在轴颈与轴承衬的180度的弧内产生时，则不同和B/d 的承载量系数C p值见表12－7。
－7。
（四）最小油膜厚度hmin由最小油膜厚度公式及承载量系数表可知，在其它条件不变的情况下，h min 愈小则偏心率愈大，轴承的承载能力就愈大。
然而，最小油膜厚度是不能无限缩小的，因为它受到轴颈和轴承表面粗糙度、轴的刚性及轴承与轴颈的几何形状误差等的限制。
为确保轴承能处于液体摩擦状态，最小油膜厚度必须等于或大于许用油膜厚度[h]，即（12－26）式中：Rz1、Rz2——分别为轴颈和轴承孔微观不平度十点高度，对一般轴承，可分别取Rz1和Rz2值为3.2μm和6.3μm，或1.6μm和3.2μm；对重要轴承可取为0.8μm和1.6μm，或0.2μm 和0.4μm。
S——安全系数，考虑表面几何形状误差和轴颈挠曲变形等，常取S≥2。
（五）轴承的热平衡计算计算原因：轴承工作时，摩擦功耗将转变为热量，使润滑油温度升高。
如果油的平均温度超过计算承载能力时所假定的数值，则轴承承载能力就要降低。
因此要计算油的温升△t，并将其限制在允许的范围内。
轴承运转中达到热平衡状态的条件：单位时间（不是单位面积）内轴承摩擦所产生的热量Q 等于同时间内流动的油所带走的热量Q1与轴承散发的热量Q2之和，即21Q Q Q =+ (12-27)轴承中的热量是由摩擦损失的功转变而来的。
因此，每秒钟在轴承中产生的热量Q为 ：Q fpv = （12－27a）由流出的油带走的热量Q1为 :()10i Q q c t t ρ=− (12-27b) 式中：q——耗油量，按耗油量系数求出，；ρ——润滑油的密度，对矿物油为850~900kg/； c——润滑油的比热容，对矿物油为1675~2090J/(kg·℃)；t 0——油的出口温度，℃；t i ——油的入口温度，通常由于冷却设备的限制，取为35~40℃。
除了润滑油带走的热量以外，还可以由轴承的金属表面通过传导和辐射把一部分热量散发到周围介质中去。
这部分热量与轴承的散热表面的面积、空气流动速度等有关，很难精确计算。
因此，通常采用近似计算。
若以H 2代表这部分热量，并以油的出口温度t 0代表轴承温度，油的入口温度代表周围介质的温度，则:()20s i Q dB t απt =− (12-27c)式中αs 为轴承的表面传热系数，随轴承结构的散热条件而定。
对于轻型结构的轴承，或周围介质温度高和难于散热的环境（如轧钢机轴承），取 αs＝50/；中型结构或一般通风条件，取αs ＝80/；在。
热平衡时，,于是得出为了达到热平衡而必须的润滑油温度差Δt 为:1Q Q Q =+2(12-28)式中：——耗油量系数，无量纲数，可根据轴承的宽径比B/d 及偏心率由图查出。
f——摩擦系数，其计算公式为，式中ξ为随轴承宽径比而变化的系数，对于B/d<1的轴承。
；B/d≥1时，ξ＝1；ω为轴颈角速度，单位为rad/s，B、d 的单位为mm；p 为轴承的平均压力，单位为Pa；η为滑油的动力粘度，单位为Pa·s。
用上式只是求出了平均温度差，实际上轴承上各点的温度是不相同的。
润滑油从入口到流出轴承，温度逐渐升高，因而在轴承中不同之处的油的粘度也将不同。
研究结果表明，在利用承载量系数公式计算轴承的承载能力时，可以采用润滑油平均温度时的粘度。
润滑油的平均温度t m =(t i +t 0)/2，而温升△t=t 0-t i ，所以润滑油的平均温度t m 按下式计算：（12－29）为了保证轴承的承载能力，建议平均温度不超过75℃。
设计时，通常是先给定平均温度t m ，按上式求出的温升Δt 来校核油的入口温度t i ,即（12－30）若t i >35~40℃，则表示轴承热平衡易于建立，轴承的承载能力尚未用尽。
此时应降低给定的平均温度，并允许适当地加大轴瓦及轴颈的表面粗糙度（这样可减小精度，增加，使承载力随之减小，与实际较小的力相匹配），再行计算。
min h 若t i <35~40℃，则表示轴承不易达到热平衡状态。
此时需加大间隙，并适当地降低轴承及轴颈的表面粗糙度，再作计算。
此外要说明的是，轴承的热平衡计算中的耗油量仅考虑了速度供油量，即由旋转轴颈从油槽带入轴承间隙的热量，忽略了油泵供油时，油被输入轴承间隙时的压力供油量，这将影响轴承温升计算的精确性。
因此，它适用于一般用途的液体动力润滑径向轴承的热平衡计算，对于重要的液体动压轴承计算可参考相关手册。
（六）参数选择1．宽径比B/d一般轴承的宽径比B/d在0.3~1.5范围内。
宽径比小，有利于提高运转稳定性，增大端泄漏量以降低温升。
但轴承宽度减小，轴承承载力也随之降低。
高速重载轴承温升高，由于温升高，宽径比宜取小值，使△t减小；低速重载轴承，需要对轴有较大支承刚性，宽径比宜取大值；高速轻载轴承，转速小高，温升大，如对轴承刚性无过高要求，可取小值；需要对轴有较大支承刚性的机床轴承，宜取较大值。
