12-07 液体动力润滑径向滑动轴承设计计算
- 格式：ppt
- 大小：747.00 KB
- 文档页数：15
下载文档原格式
合集下载
液体动力润滑滑动轴承概率设计
文献标志码 ： Ａ
文 章 编 号 ： ６ ２３ ９ （ ０ ７ ０ — ６ ００ １ ７—０ ０２ ０ ）６０ １—３
文 献［ ］ 述 常 规 液体 动 力 润 滑径 向滑 动 轴 １所 承参 数设计 方 法是 ： 按 经 验 公式 估 算 轴 颈 和轴 先 瓦之 间 的相 对 间隙 的 大概 值 ， 在 一 个 推荐 的 再 取值 范 围 内凭 经验 确 定 一 个 值 ， 后 按 取 定 然 的 值计 算承 载量 系数 Ｃ ， 而确定 滑 动轴承 的 进
外， 常规方 法在 设计 过 程 中涉 及 的一 切 轴 承参 数
（） １
设 承载 量 系数 Ｃ 是 随机变 量 ， 其分 布 服从正 态分 布 ， 可用 正 态分 布 的联结 方 程 设 计 液体 动 则
力 润滑 径 向滑动轴 承 。
都是 按定值 处 理 的。这一 点显然 与滑 动轴 承的许 多实 际参数 不相符 合 。除文献 Ｅ ］ ｂ 也 有关 于液 １￣ ， 体动力 润滑 径 向滑动 轴 承设 计 方 法 的介 绍［ ， ２ 但 ］ 采 用 的方法仍 与 文献 ［ ］ 样 。为 克 服机 械 零 件 １一 设 计 中某些 参数 选 择不 准 确 、 略 很 多设 计 参 数 忽 是 随机变 量 的现象 ， 些 研 究 者采 用 了概 率设 计 一
维普资讯
第０ ０卷 １ ２ ３ ０ ７年 第 ６期 ２月
Ｊ ｆ ｈ ｎＵｎ．ｏ ｃ ＆ Ｔ ｃ（自 然 ｒｌ ｃ ｎ） Ｅ ｉｏ ） ．ｏ 武 汉 科 技ｆ ｉ 学 报 ｈ （ ｔ 科 ｉ ｃ ｄｔ ｎ Ｗｕ ａ ｉ 大 学 Ｓ ． ｅ ． Ｎａｕａ 学 版 ｅ Ｓ ｅ ｉ
的概率 方法 。该 方法 可直接 确定满 足轴 承承 载量
流体动压润滑径向滑动轴承计算举例
流体动压润滑径向滑动轴承计算举例
试设计一流体动压润滑径向滑动轴承。
其径向外载荷为 5000N ，轴颈转速为960r/min ，轴颈所允 许的最小直
径为20mm 。
解:
工作载荷HN 〕 ^000~
轴馬宽径叱引d
卷考值 [―TT ----- 1 轴颈直径贞mm]
歹且1 00 ▼ r 自定义'
轴转速
960
开赠i 计算
混合润滑计算
rt 十算结果显示
釉承压强（MPaJ 12.5000 釉頑速度〔“旳]1 0053 r 使用参考间隍计算
3）估算轴承间隙
卩间隙计算结果显示
直径间003
相对间隙
0.0015
计算间隙
4）选择材料
包角选择n iso
ZCuSn10P1
J
许用摄大压强〔忖pa] 许用摄丈速度丽畑 许用 pv®（Mpa x m/s ） 材料属性 15
10
15 踢音洞
材料适用场合
用于中速、重戟及受变载荷的轴承.用于中速、
承°
中载的轴 参考值
轴承平均压强12.500MPa 轴承平均速度
1. OOSm/s pv® 1
2.566M Pa.m/s
5）流体动压润滑计算结果
1） 选择轴承的内径
二
101
12.5663
0.00110
席自定文相对间隙
输入自定义相对间隙值: |0.0015
匚吝输入已知裁量
轴承相
（从
略）
6）根据计算结果需要重新设计，按“返回”按钮，即可以得到可行方案。
液体动力滑动轴承的设计计算
3
取微单元进行受力分析: 取微单元进行受力分析
z
pdydz+(τ+dτ)dxdz-(p+dp)dydz –τdxdz=0 dp dτ 任意一点的油膜压力p沿x方 整理后得： 整理后得： = 向的变化率，与该点y向的 dx d y
速度梯度的导数有关。
A τ
V x p+dp
du 又有： 又有： τ=η dy
14
设计步骤 选择轴承材料， pv。 ① 选择轴承材料，验算 p、v、pv。 ②选择润滑油 ③根据直径间隙Δ，选择间隙配合 根据直径间隙Δ ④轴承工作能力校核（三个方面） 轴承工作能力校核（三个方面）
a) hmin ≥[h] 热平衡计算 校核润滑油出口油温）。 计算（ b) 热平衡计算（校核润滑油出口油温）。 c) 层流条件校核
4、轴承的热平衡计算 热平衡方程：产生的热量= 热平衡方程：产生的热量=散失的热量 Q=Q1+Q2 其中，摩擦热： 其中，摩擦热： Q=fρv W 润滑油带走的热： 润滑油带走的热：Q1 = qρc(to-ti) 轴承散发的热： Q2 =α3πdB (to-ti) 轴承散发的热： 式中: q ----润滑油流量m3/s； ----润 油流量m /s； 式中: W W
不同截面的流量是相等的
h
1 截面内的流量： b-b截面内的流量： q x = − vh 0 2
dp h 0- h 得： =6ηv --一维雷诺方程 --一维雷诺方程 3 dx h 液体动压润滑的基本方程，它描述了油膜压力p的变化与动力粘度、相对
滑动速度及油膜厚度h之间的关系。
p pmax
由上式可得压力分布曲线: 由上式可得压力分布曲线: 在b-b处：h=h0， p=pmax
取微单元进行受力分析: 取微单元进行受力分析
z
pdydz+(τ+dτ)dxdz-(p+dp)dydz –τdxdz=0 dp dτ 任意一点的油膜压力p沿x方 整理后得： 整理后得： = 向的变化率，与该点y向的 dx d y
速度梯度的导数有关。
A τ
V x p+dp
du 又有： 又有： τ=η dy
14
设计步骤 选择轴承材料， pv。 ① 选择轴承材料，验算 p、v、pv。 ②选择润滑油 ③根据直径间隙Δ，选择间隙配合 根据直径间隙Δ ④轴承工作能力校核（三个方面） 轴承工作能力校核（三个方面）
a) hmin ≥[h] 热平衡计算 校核润滑油出口油温）。 计算（ b) 热平衡计算（校核润滑油出口油温）。 c) 层流条件校核
4、轴承的热平衡计算 热平衡方程：产生的热量= 热平衡方程：产生的热量=散失的热量 Q=Q1+Q2 其中，摩擦热： 其中，摩擦热： Q=fρv W 润滑油带走的热： 润滑油带走的热：Q1 = qρc(to-ti) 轴承散发的热： Q2 =α3πdB (to-ti) 轴承散发的热： 式中: q ----润滑油流量m3/s； ----润 油流量m /s； 式中: W W
不同截面的流量是相等的
h
1 截面内的流量： b-b截面内的流量： q x = − vh 0 2
dp h 0- h 得： =6ηv --一维雷诺方程 --一维雷诺方程 3 dx h 液体动压润滑的基本方程，它描述了油膜压力p的变化与动力粘度、相对
滑动速度及油膜厚度h之间的关系。
p pmax
由上式可得压力分布曲线: 由上式可得压力分布曲线: 在b-b处：h=h0， p=pmax
液体动力润滑径向滑动轴承设计计算
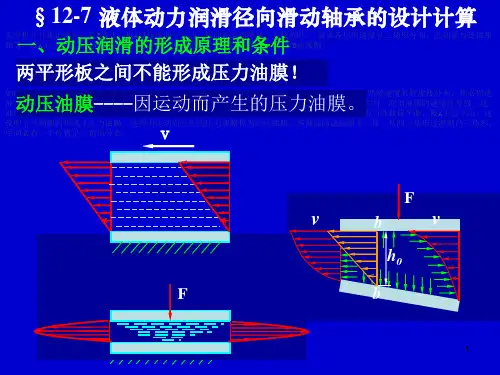
液体动力润滑径向滑动轴承设计计算流体动力润滑的楔效应承载机理已在第四章作过简要说明，本章将讨论流体动力润滑理论的基本方程（即雷诺方程）及其在液体动力润滑径向滑动轴承设计计算中的应用。
（一）流体动力润滑的基本方程流体动力润滑理论的基本方程是流体膜压力分布的微分方程。
它是从粘性流体动力学的基本方程出发，作了一些假设条件后得出的。
假设条件：流体为牛顿流体；流体膜中流体的流动是层流；忽略压力对流体粘度的影响；略去惯性力及重力的影响；认为流体不可压缩；流体膜中的压力沿膜厚方向不变。
图12－12中，两平板被润滑油隔开，设板A 沿x 轴方向以速度v 移动；另一板B 为静止。
再假定油在两平板间沿 z 轴方向没有流动(可视此运动副在z 轴方向的尺寸为无限大)。
现从层流运动的油膜中取一微单元体进行分析。
作用在此微单元体右面和左面的压力分别为p 及p p dx x ∂⎛⎞+⎜∂⎝⎠⎟，作用在单元体上、下两面的切应力分别为τ及dy y ττ⎛⎞∂+⎜⎟∂⎝⎠。
根据x 方向的平衡条件,得：整理后得根据牛顿流体摩擦定律,得，代入上式得 该式表示了压力沿x 轴方向的变化与速度沿y 轴方向的变化关系。
下面进一步介绍流体动力润滑理论的基本方程。
1．油层的速度分布将上式改写成（a）对y 积分后得（c）根据边界条件决定积分常数C1及C2:当y=0时,v= V；y=h(h为相应于所取单元体处的油膜厚度)时,v=0,则得：代入（c）式后,即得 （d）由上可见,v由两部分组成：式中前一项表示速度呈线性分布，这是直接由剪切流引起的；后一项表示速度呈抛物线分布，这是由油流沿x方向的变化所产生的压力流所引起的。
2、润滑油流量当无侧漏时,润滑油在单位时间内流经任意截面上单位宽度面积的流量为：将式(d)代入式(e)并积分后,得（f）设在 p=p max处的油膜厚度为h0(即时当润滑油连续流动时,各截面的流量相等,由此得 ：整理后得该式为一维雷诺方程。
机械设计 滑动轴承3
在图示模型中取单元体
F v
z
x h
y
对单元体列 x 方向力的平衡方程式：
解方程得： 若对 y 求导，并引入动力粘度η，得到： u
该式表明：压力沿 x 方向的变化与速度沿 y 方向的变化之 间的关系。
分析：
① 油层速度分布 2 u 1 p v 上式可改写为 y x u 积分得： v
若对雷诺方程从油膜起始角 φ 1到任意角φ 积分，可以得到 油膜的压力大小。
油膜的压力表达式：
以上压力仅只有与外载荷方向一致的分力才能 抵抗外载荷：该分量为：
Pφ Pφy
对整个承载区域进行积分，得 到轴承单位宽度上的油膜承载力：
将py乘以轴承宽度就得到轴承承载量，考虑到其 他因素影响，在ø 角和距轴承中线为Z处的油膜压力 为：
由前面已知： hmin e r 1 x 在其他条件不变时， hmin越小，x越大，轴承承载能力越 大。但由于轴承表面粗糙度、轴的刚度、轴承与轴径的 几何形状误差等限制，只有当 hmin h时，才能确保轴承 能处于液体摩擦状态。其中
h S Rz1 Rz 2
在以上假设下，从两平板所构成的楔形空间中，取某一层 液体的一部分作为单元体，通过建立平衡方程和给定边界条件， 可得一维雷诺方程：
p 6v 3 (h h0 ) x h
x c b
F
v
o
ho y
a
取楔效应分析模型进一步分析，并建立坐 标系如图，设润滑油在 z 方向不流动，即平 板 z 方向尺寸为无穷大。
2 2 2
∴
h r (1 cos )
⑦最大压力处油膜厚度h0 h0 r (1 cos 0 ) ⑧最小油膜厚度hmin
滑动轴承
◆ ◆ ◆
特
点： 有良好的流动性，可形成动压、静压或边膜界润滑膜。
适用场合：不完全液体滑动轴承和完全液体润滑滑动轴承。 选择原则：主要考虑润滑油的粘度。 转速高、压力小时，油的粘度应低一些；反之，粘度应高一些。 高温时，粘度应高一些；低温时，粘度可低一些。
三、固体润滑剂及其选择
◆
特
点：可在滑动表面形成固体膜。
③ 验算轴承的工作能力 1、平均压力p的验算
F p p Bd
F— 径向载荷, N； B— 轴瓦有效宽度,mm； d— 轴颈直径, mm； [p]— 许用压强,Mpa。 目的：防止p过高，油被挤出，产生 “过度磨损”。 2、 pv的验算 ≧ 轴承发热量∝单位面积摩擦功耗fpv ≨ pv↑→摩擦功耗↑→发热量↑→易胶合 F dn Fn pv [ pv ] MPa· m/s
衬的剥离有些相似，但疲劳剥落周边不规则，结合不良造成的 剥离则周边比较光滑。
4
腐蚀 润滑剂在使用中不断氧化，所生成的酸性物质对轴承材料
有腐蚀性，特别是对铸造铜铅合金中的铅，易受腐蚀而形成点
状的脱落。氧对锡基巴氏合金的腐蚀，会使轴承表面形成一层 由SnO2和SnO混合组成的黑色硬质覆盖层，它能擦伤轴颈表面， 并使轴承间隙变小。此外，硫对含银或含铜的轴承材料的腐蚀， 润滑油中水分对铜铅合金的腐蚀，都应予以注意。
3．根据液体润滑承载机理
液体动力润滑轴承（液体动压轴承）：无外部压力源，油 膜靠摩擦面的相对运动而自动形成。
液体静压润滑轴承：外部一定压力的流体进入摩擦面，建 立压力油膜。 本章主要讨论液体动压润滑轴承，工程中一般设计成①或②。
三、滑动轴承的特点和应用
1．优点
①轴颈与轴瓦靠面接触，可用于承受载荷特殊的 情况（重载、振动载荷、冲击载荷等）：内燃机、 汽轮机等 ②用于支承刚度要求高的情况：机床 ③用于旋转运动精度高的场合：仪表 ④用于转速特别高的场合：电机
特
点： 有良好的流动性，可形成动压、静压或边膜界润滑膜。
适用场合：不完全液体滑动轴承和完全液体润滑滑动轴承。 选择原则：主要考虑润滑油的粘度。 转速高、压力小时，油的粘度应低一些；反之，粘度应高一些。 高温时，粘度应高一些；低温时，粘度可低一些。
三、固体润滑剂及其选择
◆
特
点：可在滑动表面形成固体膜。
③ 验算轴承的工作能力 1、平均压力p的验算
F p p Bd
F— 径向载荷, N； B— 轴瓦有效宽度,mm； d— 轴颈直径, mm； [p]— 许用压强,Mpa。 目的：防止p过高，油被挤出，产生 “过度磨损”。 2、 pv的验算 ≧ 轴承发热量∝单位面积摩擦功耗fpv ≨ pv↑→摩擦功耗↑→发热量↑→易胶合 F dn Fn pv [ pv ] MPa· m/s
衬的剥离有些相似，但疲劳剥落周边不规则，结合不良造成的 剥离则周边比较光滑。
4
腐蚀 润滑剂在使用中不断氧化，所生成的酸性物质对轴承材料
有腐蚀性，特别是对铸造铜铅合金中的铅，易受腐蚀而形成点
状的脱落。氧对锡基巴氏合金的腐蚀，会使轴承表面形成一层 由SnO2和SnO混合组成的黑色硬质覆盖层，它能擦伤轴颈表面， 并使轴承间隙变小。此外，硫对含银或含铜的轴承材料的腐蚀， 润滑油中水分对铜铅合金的腐蚀，都应予以注意。
3．根据液体润滑承载机理
液体动力润滑轴承（液体动压轴承）：无外部压力源，油 膜靠摩擦面的相对运动而自动形成。
液体静压润滑轴承：外部一定压力的流体进入摩擦面，建 立压力油膜。 本章主要讨论液体动压润滑轴承，工程中一般设计成①或②。
三、滑动轴承的特点和应用
1．优点
①轴颈与轴瓦靠面接触，可用于承受载荷特殊的 情况（重载、振动载荷、冲击载荷等）：内燃机、 汽轮机等 ②用于支承刚度要求高的情况：机床 ③用于旋转运动精度高的场合：仪表 ④用于转速特别高的场合：电机
华南理工大学李旻机械设计第12章机械零件润滑设计
另外当载荷较大时，由于载荷的反复作用，轴承表面 出现与滑动方向垂直的疲劳裂纹，当裂纹向轴承衬与衬背 结合面扩展后，造成轴承衬材料的剥落。它与轴承衬和衬 背因结合不良或结合力不足造成轴承衬的剥离有些相似， 但疲劳剥落周边不规则，结合不良造成的剥离则周边比较 光滑。
2．胶合
若轴承因表面的温升过高而导致油膜破裂时，或在润 滑油供应不足的条件下，轴颈和轴承的相对运动表面材料 发生粘附和迁移，从而造成轴承损坏、咬粘，有时甚至可 能导致相对运动中止。
12.2.2 径向滑动轴承的几何关系和承载量系数
1．几何关系与膜厚计算
图12.4 径向滑动轴承几何参数与压力分布
轴承中心和轴颈中心的连线 OO1 与载荷 F（作用在
轴心）形成的夹角 a 称为偏位角。轴承孔和轴颈直径分 别用 D 和 d 表示，则轴承直径间隙为： = D – d 。半径
间隙为轴承孔半径 R 与轴颈半径 r 之差： = R – r =/2。
pV Fan [pV] 600b0z0
式中，[ pv ] —— pv 的许用值，见附表6.5。
（12.5）
上述是不完全液体润滑径向轴承的通常验算方法，对 重要的不完全液体润滑径向轴承的验算可参考有关文献。
3．非液体摩擦滑动轴承的设计
（1）径向滑动轴承设计 如果已知轴承的工况（载荷 F、转速 n），需要进行
R
若略去上式中的小量（ e ）2 sin2，并取根式的正号， R
则得任意位置的油膜厚度为
h 1 c o r s 1 c o s
（12.11）
设 0 为相应于最大压力处的极角，则压力最大处的
油膜厚度 h0为
h 01co0s （12.12）
2．Reynolds 方程求解
将式（10.30）改写成极坐标表达式，即dx = rd， V = r 及 h、h0 之值代入式（10.30）后得极坐标形式
2．胶合
若轴承因表面的温升过高而导致油膜破裂时，或在润 滑油供应不足的条件下，轴颈和轴承的相对运动表面材料 发生粘附和迁移，从而造成轴承损坏、咬粘，有时甚至可 能导致相对运动中止。
12.2.2 径向滑动轴承的几何关系和承载量系数
1．几何关系与膜厚计算
图12.4 径向滑动轴承几何参数与压力分布
轴承中心和轴颈中心的连线 OO1 与载荷 F（作用在
轴心）形成的夹角 a 称为偏位角。轴承孔和轴颈直径分 别用 D 和 d 表示，则轴承直径间隙为： = D – d 。半径
间隙为轴承孔半径 R 与轴颈半径 r 之差： = R – r =/2。
pV Fan [pV] 600b0z0
式中，[ pv ] —— pv 的许用值，见附表6.5。
（12.5）
上述是不完全液体润滑径向轴承的通常验算方法，对 重要的不完全液体润滑径向轴承的验算可参考有关文献。
3．非液体摩擦滑动轴承的设计
（1）径向滑动轴承设计 如果已知轴承的工况（载荷 F、转速 n），需要进行
R
若略去上式中的小量（ e ）2 sin2，并取根式的正号， R
则得任意位置的油膜厚度为
h 1 c o r s 1 c o s
（12.11）
设 0 为相应于最大压力处的极角，则压力最大处的
油膜厚度 h0为
h 01co0s （12.12）
2．Reynolds 方程求解
将式（10.30）改写成极坐标表达式，即dx = rd， V = r 及 h、h0 之值代入式（10.30）后得极坐标形式
油液动压径向轴承设计及计算【开题报告】
毕业设计开题报告机械设计制造及自动化油液动压径向轴承设计及计算1、选题的背景、意义流体动压径向滑动轴承具有承载能力大、功耗小、耐冲击、抗振性好、运转精度高等突出的优点。
所以，在高速、低速以及高速精密的旋转机械中应用十分普遍，而且成为旋转机械的重要部件。
比如在汽轮机组、舰船主动力机组、石油钻井机械、轧机及各类大型机床中都有广泛的应用，而且成为这类机械的关键部件之一。
在这些机器中，径向滑动轴承的性能优劣直接影响或决定了整台机器的性能和效率。
比如在汽轮发电机组中，性能优良的滑动轴承可以减少停机检修的次数，烧瓦的可能性也低得多。
轴承基本参数(轴径的长径比、半径间隙、偏心距和轴承包角等)的变化，对轴承的静动态特性会产生很大的影响。
另外，实际工作中的滑动轴承，由于加工、安装误差等因数，其工况条件与理论分析时所考虑的理想工况有很大差距，这种情况下，轴承的一些性能参数会发生变化。
2、相关研究的最新成果及动态我国轴承行业发展到现在，已具备相当的生产规模和较高的技术、质量水平。
具有一定规模的轴承企业已发展到1 500余家，职工人数壮大到近80万人，轴承年产量从1 949年的1 3．8J5套增加到目前的20多亿套，轴承品种累计从1 00多个增加至7000多个，规格达28000多个。
近1 0年来国外轴承知名公司(如SKF、FAG、NSK、NBM 、 KOYO、T JM KEN、TORRlNGTON等)先后在我国投资办厂，对我国轴承设计技术水平的提高，生产工艺和生产管理的规范、生产装备水平的现代化、产品的质量和使用性能的提高等方面起到了很大的推动作用。
2OO亿元，年出口量逾7．7亿套，出口创汇约达7亿美元，世界排名第4，满足国内所需产品品种的70％以上，满足所需数量90％以上，出口量也以较高的比例递增。
在我国跨入世界轴承生产大国行列的同时，轴承工业依然存在低、散、差的问题普通微型、小型、中小型深但另一方面，我国轴承生产企业也面临来自国外知名轴承公司的激烈竞争和挑战，其结果必将加速我国轴承工业的产业结构和严品结构的调整步伐，真可谓机遇与挑战并存、生产与发展同在。
液体动力润滑径向滑动轴承设计计算
y2 x
h
2 x
直线
抛物线
2.润滑油流量
Q
h
udy
vh
h3
p
0
2 12 x
p pmax处油膜厚为h0，即h h0
p 0 Q vh0
x
2
各截面流量相等
vh0 vh h3 p
2 2 12 x
雷诺方程：
p x
6v
h3
h
h0
p
当h＞h0时，x ＞0，p沿x方向
增大
当 h＜h0时，px＜ 0，p沿x方向
减少
流体动力润滑的必要条件：
⑴ 流体必须有粘度，供应充分
⑵ 两表面必须有相对速度，油从大口进，小口出
⑶ 相对滑动两表面必须现成收敛的楔形油隙
四 径向滑动轴承形成流体动力润滑的过程
n=0
n≥0
n＞＞0
五 径向滑动轴承的几何关系和承载量系数
1 几何关系
⑴直径、半径间隙：△=D－d，δ=R－r= △／2
结果：
F
Bd 2
Cp
承载量系数Cp
Cp
3
B/2 B/2
2 1
1
cos cos0 B1 cos 3
d
cos a
d C1
2z B
2
dz
B—轴承宽度 d—轴承直径 ω—轴承角速度
η—油的粘度 C′—与B/d和 有关的系数
Cp
F 2 Bd
F 2 2vB
讨论：
Cp (, B / d) 表12—7
八 参数选择 1 宽径比 B/d=0.3~1.5
B/d↓ 运转稳定性↑，承载能力↓ 端泄↑,△t↓
高速重载取小值 低速重载取大值
滑动轴承
滑动轴承的失效形式及常用材料
◆ 嵌入性：材料容纳硬质颗粒嵌入，从而减轻轴承滑动表面 嵌入性：材料容纳硬质颗粒嵌入， 发生刮伤或磨粒磨损的性能。 发生刮伤或磨粒磨损的性能。 ◆ 磨合性：轴瓦与轴颈表面经短期轻载运行后，形成相互吻 磨合性：轴瓦与轴颈表面经短期轻载运行后， 合的表面形状和粗糙度的能力（或性质）。 合的表面形状和粗糙度的能力（或性质）。
§12-1 滑动轴承概述
滑动轴承概述1 轴承的作用是支承轴。轴在工作时可以是旋转的， 轴承的作用是支承轴。轴在工作时可以是旋转的，也可以是 静止的。 静止的。
一、轴承应满足如下基本要求
1．能承担一定的载荷，具有一定的强度和刚度。 能承担一定的载荷，具有一定的强度和刚度。 具有小的摩擦力矩，使回转件转动灵活。 2．具有小的摩擦力矩，使回转件转动灵活。 具有一定的支承精度，保证被支承零件的回转精度。 3．具有一定的支承精度，保证被支承零件的回转精度。
滑动轴承的典型结构
２．对开式径向滑动轴承
油杯座孔 螺栓 螺母 套管 上轴瓦 轴承盖 轴承座
滑动轴承的结构2
下轴瓦
对开式轴承(剖分轴套) 对开式轴承(剖分轴套)
对开式轴承(整体轴套) 对开式轴承(整体轴套)
特点：结构复杂、可以调整磨损而造成的间隙、安装方便。 特点：结构复杂、可以调整磨损而造成的间隙、安装方便。 应用场合：低速、轻载或间歇性工作的机器中。 应用场合：低速、轻载或间歇性工作的机器中。
§12-5 滑动轴承润滑剂的选择
一、润滑脂及其选择
◆特
无流动性，可在滑动表面形成一层薄膜。 点：无流动性，可在滑动表面形成一层薄膜。 要求不高、难以经常供油， ：要求不高、难以经常供油，或者低速重载以及作摆动
◆ 适用场合
机械设计课后简答题答案
△P0。
8-12 带与带轮的摩擦系数对带传动有什么影响？为了增加传动能力，将带轮的工作面加工的粗糙些以增大摩擦系数这样做是否合理？为什么？答：摩擦系数f 增大，则带的传动能力增大，反之则减小。
这样做不合理，因为若带轮工作面加工得粗糙，则带的磨损加剧，带的寿命缩短。
8-13 带传动中的弹性滑动时如何产生的？打滑又是如何长生的？两者有何区别？对带传动各产生什么影响？打滑首先发生在哪个带轮上？为什么？答：在带传动中，带的弹性滑动是因为带的弹性变形以及传递动力时松、紧边的拉力差造成的，是带在轮上的局部滑动，弹性滑动是带传动所固有的，是不可避免的。
弹性滑动使带传动的传动比增大。
当带传动的负载过大，超过带与轮间的最大摩擦力时，将发生打滑，打滑时带在轮上全面滑动，打滑是带传动的一种失效形式，是可以避免的。
打滑首先发生在小带轮上，因为小带轮上带的包角小，带与轮间所能产生的最大摩擦力较小。
8-14 在设计带传动时，为什么要限制小带轮的最小基准直径和带的最小最大速度？答：小带轮的基准直径过小，将使V 带在小带轮上的弯曲应力过大，使带的使用寿命下降。
小带轮的基准直径过小，也使得带传递的功率过小，带的传动能力没有得到充分利用，是一种不合理的设计。
带速v 过小，带所能传递的功率也过小（因为P=Fv），带的传动能力没有得到充分利用；带速v 过大，离心力使得带的传动能力下降过大，带传动在不利条件下工作，应当避免。
8-16 题目太长，要点打出，大家自己看题目应该明白。
此题有图为带式输送机装置，小带轮的直径d1=140，大带轮基准直径为d2=400，鼓轮直径D=250 为了提高生产效率有以下三个方案，分析方案的合理性？为什么？方案—：将大带轮的直径减小到280 方案二：将小带轮的直径增大至200 方案三：将鼓轮直径D 增大到350 答：输送机的F 不变，v 提高30%左右，则输出功率增大30%左右。
三种方案都可以使输送带的速度v 提高，但V 带传动的工作能力却是不同的。
12-07 液体动力润滑径向滑动轴承设计计算
12.7.8 参数选择
被油膜隔开的两平板的相对运动情况
p
x h 该式为一维雷诺方程，它是计算流体动力润滑滑动轴 承的基本方程，由方程可以看出，油膜压力的变化与润滑 油的粘度、表面滑动速度和厚度及其变化有关。
3
6v
(h h0 )
形成液体动力润滑的必要条件
（1）相对运动的两表面必须形成收敛的楔形间隙；
在其它条件不变的情况下，hmin愈小则偏心率χ愈大，轴承 的承载能力就愈大。
式中：Rz1、Rz2－－分别为轴颈和轴承孔表面粗糙度十点高度；
S－－安全系数，常取S≥2。
轴承的热平衡计算
热平衡条件： 轴承单位时间产生的热量： 由流出的油带走的热量： Q=Q1+Q2 Q=fpv Q1=qρc ( t0-ti )
直径间隙
半径间隙
相对间隙 偏心距e
偏心率
最小油膜厚度
（四）径向滑动轴承工作能力计算简介
不同宽径比时沿轴承周向和轴向的压力分布：
有限宽轴承的承载量系数 Cp
对于有限宽轴承，油膜的总承载能力为：
承载量系数：
当轴承的包角一定时，经过一系列的换算，Cp可以表示为：
有限宽轴承的承载量系数 Cp
最小油膜厚度hmin
（2）被油膜分开的两表面必须有一定的相对滑动速度， 其运动方向必须使润滑油由大口流进，从小口流出； （3）润滑油必须有一定的粘度，供油要充分。
（二）径向滑动轴承形成液体动力润滑的过程
停车
刚启动
转速不高
径向滑动轴承形成液体动力润滑的过程
转速达到一定值
转速趋于无穷大
（三）径向滑动轴承的几何参数和油压分布
12-7 液体动力润滑径向滑动轴承设计
及液体动力润滑轴承的初步计算
特 点 应 用
铜合金
类 型
锡青铜 铅青铜 铝青铜 锡青铜减摩性和耐磨性最好，
特 点
铅青铜抗粘附能力强，
铝青铜强度及硬度较高。 锡青铜适用于重载、中速场合，
应 用
铅青铜适用于高速、重载场合， 铝青铜适用于低速、重载场合。
17.4 轴瓦结构 17.4.1 轴瓦和轴承衬
剖 分 式
整 体 式
轴瓦结构
轴瓦的定位
3.限制滑动速度v 限制局部的过度磨损
v
dn
60 1000
v
17.7.2 的平均压力Ｐ
n
d0
F p A
z
F
2 2 d0
d 4
p
推力滑动轴承
２）验算轴承的pV 值 Fn pv pv 4 3 10 (d d 0 ) z
17.5.2 润滑脂 特 点：无流动性，可在滑动表面形成一层薄膜。 适用场合 ：要求不高、难以经常供油，或者低速重载以 及作摆动运动的轴承中。 选择润滑脂品种的一般原则 1.单位压力高和滑动速度低时，选择针入度小一些的 品种； 2.所用润滑脂的滴点，一般应高于轴承工作温度约 20º ~30º C; 3.在有水淋或潮湿的环境下，应选择防水性强的钙基 或铝基脂；在温度较高时应选用钠基或锂基脂。
凸 缘
17.4.2 油孔、油沟和油室
目的：把润滑油导入轴颈和轴承所构成的运动副表面。
设计油沟时应注意的问题： 1、 油沟长度一般为轴承长度的80%； 2、 油孔、油沟应开在非承载区。
17.5 轴承润滑材料 17.5.1 润滑油 特点： 有良好的流动性，可形成动压、静压或边膜界 润滑膜。 适用场合：不完全液体滑动轴承和完全液体润滑滑动 轴承。 粘度选择的原则： 1.转速高，比压小时，选粘度低的油；反之，选粘度高 的油； 2.加工表面粗糙度高时，选粘度大的油； 3.根据润滑方式不同，选择不同粘度的油； 4.在较高温度下工作的轴承，所用油的粘度比通常高一 些； 5.低温工作的轴承应选用凝点低的油。
13.8液体动力润滑径向轴承的计算
学提供
3 4 ( 0 . 6 ~ 1 . 0 ) 10 v 经验公式：
机械设计
粘度
23
轴承温度近似等于油的平均温度tm，tm低，粘度大，算出的承载能 力偏高；反之，承载能力偏低。
设计时，可先假定平均温度，一般取tm=50～75℃（初选），通 过热平衡计算来验算轴承入口油温t1是否在30～40℃之间，否则 重新选择粘度在作计算。 对于一般轴承可按下式初估油的动力粘度，即
Rz1，Rz2
2n Rr rad / s ，S=2， 60 r
F 2 CP Bd
η、v（n）、B、F
机械设计
26
根据CP，查CP-表，得 。
hmin r (1 )
若 h S (R R ) ：形成流体动压润滑 min z1 z2
否则，不能形成动压润滑，措施：
机械设计
15
C
—润滑油的比热容，对矿物油为1675～209J/(kg ·℃) —润滑油的密度，对矿物油为850～900kg/m3
s —轴承的表面传热系数，随轴承结构的散热条件而定
s 50W / (m 2 C)(散热差)
s 140W / (m 2 C)(散热好)
热平衡条件：
机械设计
6
任一位置
处，油膜厚度h：
h OD Od OM MD Od e cos R r cos
∴
h (1 cos ) r (1 cos )
OO 与外载F方向之间的夹角。
偏位角θ：连心线
机械设计
2 1
机械设计
10
F 2 f ( , , B / d ) CP Bd
3 4 ( 0 . 6 ~ 1 . 0 ) 10 v 经验公式：
机械设计
粘度
23
轴承温度近似等于油的平均温度tm，tm低，粘度大，算出的承载能 力偏高；反之，承载能力偏低。
设计时，可先假定平均温度，一般取tm=50～75℃（初选），通 过热平衡计算来验算轴承入口油温t1是否在30～40℃之间，否则 重新选择粘度在作计算。 对于一般轴承可按下式初估油的动力粘度，即
Rz1，Rz2
2n Rr rad / s ，S=2， 60 r
F 2 CP Bd
η、v（n）、B、F
机械设计
26
根据CP，查CP-表，得 。
hmin r (1 )
若 h S (R R ) ：形成流体动压润滑 min z1 z2
否则，不能形成动压润滑，措施：
机械设计
15
C
—润滑油的比热容，对矿物油为1675～209J/(kg ·℃) —润滑油的密度，对矿物油为850～900kg/m3
s —轴承的表面传热系数，随轴承结构的散热条件而定
s 50W / (m 2 C)(散热差)
s 140W / (m 2 C)(散热好)
热平衡条件：
机械设计
6
任一位置
处，油膜厚度h：
h OD Od OM MD Od e cos R r cos
∴
h (1 cos ) r (1 cos )
OO 与外载F方向之间的夹角。
偏位角θ：连心线
机械设计
2 1
机械设计
10
F 2 f ( , , B / d ) CP Bd
液体动力润滑径向滑动轴承设计计算
液体动力润滑径向滑动轴承设计计算流体动力润滑的楔效应承载机理已在第四章作过简要说明，本章将讨论流体动力润滑理论的基本方程（即雷诺方程）及其在液体动力润滑径向滑动轴承设计计算中的应用。
（一）流体动力润滑的基本方程流体动力润滑理论的基本方程是流体膜压力分布的微分方程。
它是从粘性流体动力学的基本方程出发，作了一些假设条件后得出的。
假设条件：流体为牛顿流体；流体膜中流体的流动是层流；忽略压力对流体粘度的影响；略去惯性力及重力的影响；认为流体不可压缩；流体膜中的压力沿膜厚方向不变。
图12－12中，两平板被润滑油隔开，设板A 沿x 轴方向以速度v 移动；另一板B 为静止。
再假定油在两平板间沿 z 轴方向没有流动(可视此运动副在z 轴方向的尺寸为无限大)。
现从层流运动的油膜中取一微单元体进行分析。
作用在此微单元体右面和左面的压力分别为p 及p p dx x ∂⎛⎞+⎜∂⎝⎠⎟，作用在单元体上、下两面的切应力分别为τ及dy y ττ⎛⎞∂+⎜⎟∂⎝⎠。
根据x 方向的平衡条件,得：整理后得根据牛顿流体摩擦定律,得，代入上式得 该式表示了压力沿x 轴方向的变化与速度沿y 轴方向的变化关系。
下面进一步介绍流体动力润滑理论的基本方程。
1．油层的速度分布将上式改写成（a）对y 积分后得（c）根据边界条件决定积分常数C1及C2:当y=0时,v= V；y=h(h为相应于所取单元体处的油膜厚度)时,v=0,则得：代入（c）式后,即得 （d）由上可见,v由两部分组成：式中前一项表示速度呈线性分布，这是直接由剪切流引起的；后一项表示速度呈抛物线分布，这是由油流沿x方向的变化所产生的压力流所引起的。
2、润滑油流量当无侧漏时,润滑油在单位时间内流经任意截面上单位宽度面积的流量为：将式(d)代入式(e)并积分后,得（f）设在 p=p max处的油膜厚度为h0(即时当润滑油连续流动时,各截面的流量相等,由此得 ：整理后得该式为一维雷诺方程。
液体动压径向滑动轴承设计与分析
液体动压径向滑动轴承设计与分析摘要动压式滑动轴承是轴承中的一个重要类别，对其进行分析研究在实际中具有重要意义。
液体动压径向滑动是其中的重要一类，本文以径向滑动轴承为研究对象，以雷诺方程的建立及求解过程为理论基础，对滑动轴承在处于液体动压的工况情况进行理论分析。
本课题的目的就是旨在结合滑动轴承的工作特点和性能，合理的优化轴承的结构形式，对轴承的各性能进行优化设计。
通过图纸对轴承结构进行分析优化，利用相关公式对性能进行计算与分析，对整个轴承进行优化设计。
关键字：滑动轴承；雷诺方程目录第一章1绪论 (4)1.1本课题的选定 (5)1.2滑动轴承制造和生产技术的发展现状 (5)1.3本课题研究的主要内容及基本工作思路 (6)(一)主要内容 (6)（二）本课题基本工作思路 (6)第二章2液体动压径向滑动轴承的总体设计方案 (6)2.1滑动轴承 (6)（一）滑动轴承的主要类型和结构 (6)2.2液体动压润滑的基本原理和基本关系 (8)（一）液体动压油膜的形成理论 (8)（二）液体动压润滑的基本方程 (8)（三）油楔承载机理 (11)2.3液体动压径向滑动轴承基本原理 (11)（一）径向滑动轴承液体动压润滑的建立过程 (11)(二)径向滑动轴承的几何关系和承载能力 (12)（三）径向滑动轴承的参数选择 (16)（四）径向滑动轴承的供油结构 (18)第三章3液体动压径向滑动轴承的实例计算 (20)3.1主要技术指标 (20)3.2选择轴承材料和结构 (20)3.3润滑剂和润滑方法的选择 (21)3.4性能计算 (21)（一）承载能力计算 (21)（二）层流校核 (22)（三）功耗计算 (22)（四）热平衡计算 (23)（五）安全度计算 (23)第四章4三维建模4.1三维建模依据 (23)4.2三维建模的基本图形 (24)4.3三维建模的步骤 (24)总结 (25)参考文献 (25)致谢 (27)附件外文翻译文献第一章1绪论滑动轴承在机械制造、大型电站、钢铁联合企业以及化工联合企业等机械设备中得到广泛应用，如何提高其寿命和工作可靠性越来越成为人类普遍关注的问题。
机械设计课件濮良贵版本12
◆ 两板相对运动的结果，应使液体在粘性力的作用下由楔形空间的大端 流向楔形空间的小端 。
详细推导
液体动力润滑径向滑动轴承的设计计算
二、径向滑动轴承形成流体动力润滑时的状态
◆ 轴承的孔径D和轴颈的直径d名义尺寸相等；直径间隙Δ是公差形成的。
◆ 轴颈上作用的液体压力与F相平衡，在与F垂直的方向，合力为零。
◆ 多环式：不仅能承受较大的轴向载荷，有时还可承受双向轴向载荷。 由于各环间载荷分布不均，其单位面积的承载能力比单环式低50%。
空心式
单环式
多环式
汽车用滑动轴承故障原因的平均比率
轴承表面的磨粒磨损、刮伤、咬粘(胶合)、疲劳剥落和腐蚀。
一、滑动轴承常见失效形式有：
滑动轴承还可能出现气蚀、电侵蚀、流体侵蚀和微动磨损等失效形式。
３．承受巨大的冲击与振动载荷，如轧钢机。
４．特重型的载荷，如水轮发电机。
５．根据装配要求必须制成剖分式的轴承，如曲轴轴承。
６．在特殊条件下工作的轴承，如军舰推进器的轴承。
７．径向尺寸受限制时，如多辊轧钢机。
轴承的型式和结构选择；轴瓦的结构和材料选择；轴承的结构参数设计；
润滑剂及其供应量的确定；轴承工作能力及热平衡计算。
§12-1 滑动轴承概述
§12-2 滑动轴承的典型结构
§12-3 滑动轴承的失效形式及常用材料
§12-4 滑动轴承轴瓦结构
§12-5 滑动轴承润滑剂的选择
§12-6 不完全液体润滑滑动轴承的设计计算
§12-7 液体动力润滑径向滑动轴承的设计计算
§12-8 其它形式滑动轴承简介
第十二章 滑动轴承
滑动轴承概述
滑动轴承的典型结构
一、径向滑动轴承的结构
１．整体式径向滑动轴承
详细推导
液体动力润滑径向滑动轴承的设计计算
二、径向滑动轴承形成流体动力润滑时的状态
◆ 轴承的孔径D和轴颈的直径d名义尺寸相等；直径间隙Δ是公差形成的。
◆ 轴颈上作用的液体压力与F相平衡，在与F垂直的方向，合力为零。
◆ 多环式：不仅能承受较大的轴向载荷，有时还可承受双向轴向载荷。 由于各环间载荷分布不均，其单位面积的承载能力比单环式低50%。
空心式
单环式
多环式
汽车用滑动轴承故障原因的平均比率
轴承表面的磨粒磨损、刮伤、咬粘(胶合)、疲劳剥落和腐蚀。
一、滑动轴承常见失效形式有：
滑动轴承还可能出现气蚀、电侵蚀、流体侵蚀和微动磨损等失效形式。
３．承受巨大的冲击与振动载荷，如轧钢机。
４．特重型的载荷，如水轮发电机。
５．根据装配要求必须制成剖分式的轴承，如曲轴轴承。
６．在特殊条件下工作的轴承，如军舰推进器的轴承。
７．径向尺寸受限制时，如多辊轧钢机。
轴承的型式和结构选择；轴瓦的结构和材料选择；轴承的结构参数设计；
润滑剂及其供应量的确定；轴承工作能力及热平衡计算。
§12-1 滑动轴承概述
§12-2 滑动轴承的典型结构
§12-3 滑动轴承的失效形式及常用材料
§12-4 滑动轴承轴瓦结构
§12-5 滑动轴承润滑剂的选择
§12-6 不完全液体润滑滑动轴承的设计计算
§12-7 液体动力润滑径向滑动轴承的设计计算
§12-8 其它形式滑动轴承简介
第十二章 滑动轴承
滑动轴承概述
滑动轴承的典型结构
一、径向滑动轴承的结构
１．整体式径向滑动轴承
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
（二）径向滑动轴承形成液体动力润滑的过程
停车
刚启动
转速不高
径向滑动轴承形成液体动力润滑的过程
转速达到一定值 转速趋于无穷大
（三）径向滑动轴承的几何参数和油压分布
直径间隙 半径间隙 相对间隙 偏心距e 偏心率
最小油膜厚度
（四）径向滑动轴承工作能力计算简介
不同宽径比时沿轴承周向和轴向的压力分布：
有限宽轴承的承载量系数 Cp
对于有限宽轴承，油膜的总承载能力为：
承载量系数：
当轴承的包角一定时，经过一系列的换算，Cp可以表示为：
有限宽轴承的承载量系数 Cp
最小油膜厚度hmin
在其它条件不变的情况下，hmin愈小则偏心率χ愈大轴承 的承载能力就愈大。
式中：Rz1、Rz2－－分别为轴颈和轴承孔表面粗糙度十点高度；
12-7 液体动力润滑径向滑动轴承设计
12.7.1 形成液体动力润滑的必要条件 12.7.2 径向滑动轴承形成液体动力润滑的过程 12.7.3 径向滑动轴承的几何参数和油压分布 12.7.4 不同宽径比时沿轴承周向和轴向的压力分布 12.7.5 承载量系数 Cp 12.7.6 最小油膜厚度hmin 12.7.7 轴承的热平衡计算 12.7.8 参数选择
（五）参数选择
（2）相对间隙ψ • 速度↑,ψ↑ • 载荷↑,ψ↓
按转速取ψ 值的经验公式为：
一般机器中常用的ψ 值为： 汽轮机、电动机、齿轮减速器：0.001-0.002； 轧钢机、铁路车辆：0.0002-0.0015。
（五）参数选择
（3）粘度η
按轴颈转速n先初估油的动力粘度η’：
被油膜隔开的两平板的相对运动情况
p x
6v
h3
(h
h0 )
该式为一维雷诺方程，它是计算流体动力润滑滑动轴
承的基本方程，由方程可以看出，油膜压力的变化与润滑
油的粘度、表面滑动速度和厚度及其变化有关。
形成液体动力润滑的必要条件
（1）相对运动的两表面必须形成收敛的楔形间隙； （2）被油膜分开的两表面必须有一定的相对滑动速度， 其运动方向必须使润滑油由大口流进，从小口流出； （3）润滑油必须有一定的粘度，供油要充分。
S－－安全系数，常取S≥2。
轴承的热平衡计算
热平衡条件： 轴承单位时间产生的热量：
Q=Q1+Q2 Q=fpv
由流出的油带走的热量：
Q1=qρc ( t0-ti )
由轴承的金属表面通过传导和辐射散发的热量：
Q2=αSπdB ( t0-ti ) 为了达到热平衡而必须的润滑油温度差为:
润滑油流量系数
（五）参数选择
（1）宽径比B/d 一般轴承：0.3～1.5 B/d↓,运动稳定性↑,端泄量↑,温升↓ B/d↑,承载能力↑
高速重载轴承： 温升高,B/d 取小值； 低速重载轴承： 为了提高轴承刚性, B/d 取大值； 高速轻载轴承： 如对轴承刚性无过高要求, B/d 取小 值； 轴承刚性要求高： B/d 取大值。