平行四边形中的基本图形

ppt课件•平行四边形基本概念与性质•平行四边形面积计算公式推导•实际应用举例与计算技巧•常见误区及纠正方法目录•拓展延伸：其他相关几何图形面积计算•总结回顾与课堂互动环节平行四边形基本概念与性质01定义及特点定义两组对边分别平行的四边形叫做平行四边形。

特点对角线互相平分；对边平行且相等；对角相等，邻角互补。

平行四边形与矩形、正方形关系矩形有一个角是直角的平行四边形是矩形。

矩形具有平行四边形的所有性质，同时其对角线相等且互相平分。

正方形一组邻边相等的矩形是正方形。

正方形具有矩形和平行四边形的所有性质，同时其对角线相等、互相垂直且互相平分。

010204性质总结平行四边形的对边平行且相等。

平行四边形的对角相等，邻角互补。

平行四边形的对角线互相平分。

平行四边形的面积等于底和高的乘积，即S=ah（其中a为底，h为高）。

03平行四边形面积计算公式推导02基于矩形面积公式推导割补法将平行四边形沿高线切割成两部分，通过平移和旋转拼成一个矩形，从而得出平行四边形的面积等于底乘以高。

等积变形法通过等积变形，将平行四边形转化为一个与其面积相等的矩形，从而推导出平行四边形的面积公式。

基于三角形面积公式推导三角形面积公式三角形的面积等于底乘以高的一半。

对于平行四边形，可以将其划分为两个等底等高的三角形，因此平行四边形的面积等于两个三角形面积之和，即底乘以高。

间接推导法通过证明平行四边形的对角线将其分成两个面积相等的三角形，再利用三角形面积公式推导出平行四边形的面积公式。

不同方法比较与优缺点分析方法比较基于矩形面积公式推导的方法更加直观易懂，适用于初学者；而基于三角形面积公式推导的方法则更加严谨，但需要一定的几何基础。

优缺点分析基于矩形面积公式推导的方法优点是简单易懂，缺点是对于某些特殊情况可能不太适用；而基于三角形面积公式推导的方法优点是严谨性强，适用范围广，缺点是对于初学者可能较难理解。

在实际应用中，可以根据具体情况选择合适的方法进行计算。

平行四边形的定义、性质与判定作者：田载今来源：《中学生数理化·八年级数学人教版》2015年第03期人教版初中数学教科书的第十八章《平行四边形》的主要内容有：（一）平行四边形的定义、性质和判定；（二）特殊的平行四边形（矩形、菱形和正方形）的定义、性质和判定，通过学习这些内容，同学们将对几何图形中的一类重要图形——平行四边形有更深入的认识.一、一般平行四边形的定义、性质和判定1.定义同学们在小学数学中已经接触过平行四边形.在现实世界中，形状为平行四边形的物体比比皆是.图1是一个花坛的平面图，它由三种形状不同的平行四边形组成.每种平行四边形各有4个，安排在不同的位置上，一种几何图形的内涵式定义，是对这种图形最基本的特征的揭示.尽管有形形色色的平行四边形，但它们都有共同的最基本的特征，即“两组对边分别平行”.于是，平行四边形就被定义为：两组对边分别平行的四边形.2.性质研究图形的性质，就是在确定考查的对象是某种图形后，再考虑还有哪些结论适合于它.虽然一种图形的定义给出了这种图形的最基本的特征，但是定义本身不一定能够直接反映出这种图形的所有性质.通常，我们可以利用定义进一步推导出图形所具有的最基本特征之外的其他特性，根据平行四边形是“两组对边分别平行的四边形”，利用三角形全等就可以推导出平行四边形的“对边相等”“对角相等”“对角线互相平分”等一系列性质.在这些性质的推导过程（如图2）中，三角形这一最简单的多边形发挥了重要的作用.实际上，图形的所有性质都是由图形的定义确定的.虽然定义本身并未直接表述出所有的性质，但是在定义中已经隐含了它们.以定义为出发点，可以逐步推导出所有的性质.教科书中通常在给出一种图形的定义后，会继续讨论由它能进一步推出哪些结论，即得出经常会用到的这种图形的某些主要性质.当然，这种图形很可能还有一些教科书未曾提及的其他性质.例如，平行四边形除了具有教科书中所说的“对边平行且相等”“对角相等”“对角线互相平分”等主要性质之外，还有“对角线的平方和等于四条边的平方和”这个性质.它可以证明如下，如图3，作平行四边形ABCD的高线DE.CF.利用全等三角形可以证明AE=BF.3.判定图形的判定，是讨论图形时须研究的另一类问题.这是指，当一个对象满足哪些条件时，就可以确定它属于某种图形的范畴.例如，当一个图形满足哪些条件时，就可以确定它是平行四边形.除了用是否符合定义来判断一个对象是否属于某种图形的范畴之外，还可以通过检验对象是否满足定义以外的一些其他条件，来完成这样的判断.这样的条件叫做判定条件.所谓判定条件，就是可以由其推导出“定义巾的条件”的那些条件，例如，我们看一个四边形是否为平行叫边形，可以看它是否满足“一组对边平行且相等”或者“两组对边分别相等”或者“两组对角分别相等”或者“对角线互相平分”，因为由这些条件叶1的任何一个条件，都可以推导出四边形的“两组对边分别平行”，所以满足上述任何一个条件的四边形都是平行四边形.在得出这些判定条件的推导过程中，同样利用了全等三角形，例如，由四边形的“对角线互相平分”，通过全等三角形，可以推导出“对边互相平行”（图4）.4.“性质”和“判定”的关系图形的性质和判定，是两类不同的问题，讨论一种图形的性质，是在确定对象已经是某种图形的前提下进行的；讨论一种图形的判定，是为了确定对象是某种图形.有时，在分析某个问题的过程中，这两类问题都会出现.请看下面的问题.已知在四边形ABCD中，对角线AC和BD互相平分，试问：四边形ABCD的四条边与两条对角线有什么关系？由对角线AC和BD互相平分，可以知道四边形ABCD是平行四边形.由此又可以知道AB²+BC²+CD²+DA²=AC²+BD²，即四边形ABCD的四条边的平方和等于对角线的平方和.在这个问题的分析过程中，既有“判定”又有“性质”.第一步是判定四边形ABCD是平行四边形，第二步则是应用了前面说过的平行四边形的性质，一种图形具有某条性质，是否就可以反过来把这条性质当作这种图形的一个判定条件呢？不是，并不是一种图形的每个性质都可以拿来作为这种图形的判定条件的.例如，平行四边形也具有“内角和为360°”的性质，但这是任一四边形都具有的性质，所以它并不能作为平行四边形的判定条件.有些性质是平行四边形所独有的，其他图形不具备，例如“对边相等”“对角相等”“对角线互相平分”等，这样的性质才可以反过来作为平行四边形的判定条件，二、特殊平行四边形的定义、性质和判定矩形、菱形和正方形是三种特殊的平行四边形.1.定义特殊图形的定义方式，通常是以一般图形为基础，再加上特殊图形的最基本的特征.这些特征是区别特殊图形与其他图形的标志.特殊平行四边形的定义结构：同学们会发现，矩形和菱形都是以平行四边形为基础再加上特殊限定条件而定义的，所以它们是特殊的平行四边形.而正方形显然是在四边形的基础上定义的，为什么也说它是特殊的平行四边形呢？正方形即正四边形，而正n边形统一定义为“n条边都相等，n个角都相等的n 边形”，所以正方形采川了如上的定义.但由正四边形的“四条边都相等”或“四个角都相等”，都可判定正四边形是平行四边形，所以正方形是特殊的平行四边形，而且它兼具菱形和矩形的基本特征.它是特征更多的平行四边形.四边形、平行四边形、矩形、菱形和正方形之间的关系如图5所示.图6也能表示平行四边形、矩形、菱形和正方形之间的包含和从属关系.2.性质特殊平行四边形除了具有一般平行四边形的性质之外，还有它自己的特性，从特殊平行四边形的定义出发，利用它的最基本的特征，还可以进一步得出一些其他特性.这些推导要用到一般平行四边形的性质以及全等三角形的性质等.3.判定特殊的平行四边形除了可以根据定义判定之外，还有一些其他的判定条件，推导这些判定条件要用到一般平行四边形的性质以及全等三角形的性质等，边、角和对角线是四边形中的基本元素，也是判定条件中的考查对象，只有当它们满足判定条件中的全部要求时，才能作出判定.只满足判定条件中的部分要求时，则不能下结论.例如，对角线要满足“相等”“互相垂直”“互相平分”三个条件时，才能判定四边形是正方形.如果只知道一个四边形的“对角线相等且互相垂直”，则不能轻易断定该四边形是正方形，图7的筝形就是反例，它的两条对角线相等且互相垂直，但不满足“互相平分”，显然它不是正方形，也不是平行四边形.。

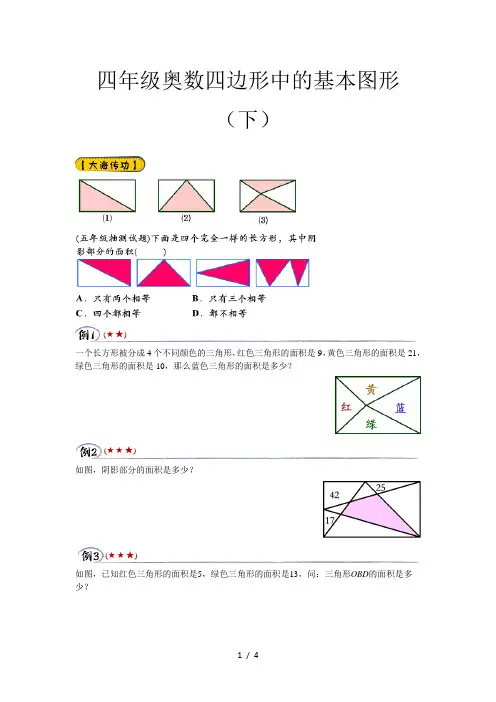
四年级奥数四边形中的基本图形（下）(★★)一个长方形被分成4个不同颜色的三角形，红色三角形的面积是9，黄色三角形的面积是21，绿色三角形的面积是10，那么蓝色三角形的面积是多少？(★★★)如图，阴影部分的面积是多少？(★★★)如图，已知红色三角形的面积是5，绿色三角形的面积是13，问：三角形OBD的面积是多少？如图，正方形ABCD的边长是4厘米，矩形DEFG的长EF＝5厘米，求它的宽DE＝？如图，正方形ABCD的边长为8，AE＝2，CF＝3。

长方形EFGH的面积为_______。

如图，ABCD是梯形，ABFD是平行四边形，CDEF是正方形，AGHF是长方形。

又知AD＝1 4厘米，BC＝22厘米，那么阴影部分的面积是多少平方厘米？(★★★★★)(第五届走美试题改编) (★★★★)(★★★★)在线测试题温馨提示：请在线作答，以便及时反馈孩子的薄弱环节！1．(★★)一个长方形被分成4个不同三角形，已知阴影部分的面积分别是8、24、6，那么空白部分三角形的面积是多少？A．24 B．20 C．26 D．2886？242．(★★★)如图，已知阴影部分的面积是36，那么甲＋乙＋丙的面积之和是多少？A．24 B．32 C．39 D．36丙36乙甲3．(★★★★)如图，三角形AOD的面积是8平方厘米，三角形DOC的面积是17平方厘米。

那么三角形DOB的面积是多少平方厘米？A．9 B．12 C．5 D．74．(★★★★)如图所示，正方形ABCD 的边长为8厘米，长方形EBGF 的长BG 为10厘米，那么长方形的宽为几厘米？ A ．6 B ．5.6 C ．6.4 D ．3.8A BGC E FD5．(★★★★★)如图，正方形ABCD 的边长为6，AE =1.5，CF =2。

长方形EFGH 的面积为 。

A ．30 B ．33 C ．29 D ．16.5HGF EDCBA6．(★★★★)如图，ABCD 是梯形，ABFD 是平行四边形，CDEF 是正方形，AGHF 是长方形。

平面几何平行四边形的性质平行四边形是平面几何中一种重要的图形，具有独特的性质和特征。

本文将介绍平行四边形的定义、性质以及相关定理，探讨其在几何学中的应用。

一、平行四边形的定义平行四边形是指四边形的对边两两平行的四边形。

简单来说，对于一个四边形，如果它的对边互相平行，则称之为平行四边形。

除了对边平行外，平行四边形还具有其他重要的性质。

二、平行四边形的性质1. 对边性质：平行四边形的对边长度相等。

这意味着平行四边形的相对边长是相等的，可以用于解题和判断。

2. 对角线性质：平行四边形的对角线互相平分。

具体而言，平行四边形的对角线AB和CD交于E点，那么AE和EC的长度相等，BE和ED的长度也相等。

3. 对角线垂直性质：平行四边形的对角线互相垂直。

即平行四边形的对角线交于一点时，也是互相垂直的。

4. 同位角性质：平行四边形的同位角相等。

同位角是指位于平行四边形相邻顶点之间的内角，这些角的度数是相等的。

5. 内角和性质：平行四边形的内角和为360度。

我们可以通过这个性质来验证一个四边形是否为平行四边形。

三、平行四边形的相关定理除了上述的基本性质外，还有一些与平行四边形相关的定理。

1. 平行四边形的定理：如果一个四边形的对边互相平行，则它是一个平行四边形。

2. 平行四边形的推论定理：如果一个四边形的对边长度相等，则它是一个平行四边形。

3. 平行四边形的性质定理：如果一个四边形的对角线互相垂直，则它是一个平行四边形。

以上定理可以帮助我们在解题过程中判断和证明一个四边形是否为平行四边形，并且使用这些定理可以简化证明过程，提高解题效率。

四、平行四边形的应用平行四边形在几何学中有广泛的应用。

下面列举几个常见的应用场景：1. 计算面积：平行四边形的面积计算公式为面积 = 底边长 ×高度。

通过求解平行四边形的面积，我们可以对平行四边形进行比较和分类。

2. 证明性质：平行四边形的性质可以在证明过程中起到重要的作用。

四边形的性质和分类四边形是一种几何图形，由四条边和四个顶点组成。

在数学中，四边形有着丰富的性质和分类。

本文将介绍四边形的基本定义、性质和常见分类。

一、四边形的基本定义四边形是由四条线段相连组成的几何图形。

它的特点是具有四个内角和四个外角。

四边形的边相交于顶点，形成内角，而顶点和顶点之间的直线形成外角。

二、四边形的性质1. 内角和四边形的内角和等于360度。

也就是说，四边形的四个内角之和始终为360度。

这一性质可以通过将四边形划分成两个三角形来证明。

因为三角形的三个内角和等于180度，所以两个三角形的内角和加起来等于360度。

2. 对角线四边形的对角线是连接非相邻顶点的线段。

对角线有两条，它们分别把四边形分成两个对称的三角形。

对角线的长度可以通过使用勾股定理来计算。

3. 相邻角四边形的相邻角是指共享一条边的两个角。

相邻角的和等于180度，即补角。

这一性质也可以通过将四边形划分成两个三角形来证明。

4. 平行四边形平行四边形是指具有两组平行边的四边形。

它的对边长度相等，对角线相互平分，并且内角相互补角。

平行四边形是四边形中最基本的形式之一。

5. 矩形矩形是一种特殊的平行四边形，它的所有内角都是直角，即90度。

矩形的对边相等且平行，对角线长度相等。

矩形是一种常见的四边形，也是我们日常生活中最常见的几何形状之一。

6. 正方形正方形是一种特殊的矩形，它的所有边和内角都相等。

正方形也是一种特殊的菱形，具有对角线相等且互相垂直的性质。

正方形是对称性最好的四边形，具有许多特殊性质，如面积和周长的关系等。

三、四边形的分类根据四边形的性质和特点，我们可以将其分为以下几类：1. 平行四边形平行四边形具有平行的边和相等的对角线。

常见的平行四边形有矩形、正方形、菱形等。

2. 等腰四边形等腰四边形具有两对相等的边。

根据内角的不同，等腰四边形又可分为等腰梯形、等腰平行四边形等。

3. 等边四边形等边四边形的四条边都相等。

正方形是一种特殊的等边四边形。

解析几何中的平行四边形特性平行四边形是解析几何中的一种基本图形，它具有许多特性和性质。

在本文中，我将详细解析几何中平行四边形的特性，包括定义、性质和相关定理。

一、定义平行四边形是指一种具有四条边都平行的四边形。

在平行四边形中，相邻边两两平行，相对边两两相等。

平行四边形的特点使得它在解析几何中具有重要的应用价值。

二、特性和性质1. 对角线等分平行四边形的对角线互相等分。

即对角线将平行四边形分成两个相等的三角形。

这一性质可以通过应用平行线的性质进行证明。

2. 对边相等平行四边形的对边互相相等。

这一性质可以通过使用平行线的性质以及等边三角形的性质进行证明。

3. 内角和为360度平行四边形的内角和等于360度。

这是因为平行四边形可以分割成两个相等的三角形，而三角形的内角和为180度，所以两个三角形的内角和加起来为360度。

4. 对角线的交点平行四边形的对角线交点将对角线平分，并且对角线和对角线之间的线段成比例。

这一特性十分有用，在解析几何的证明中经常被应用。

三、相关定理1. 平行四边形的定理平行四边形的定理包括：如果一个四边形的对边互相平行并且相等，则它是一个平行四边形。

这一定理是判定一个四边形是否为平行四边形的重要准则。

2. 平行四边形的约定定理平行四边形的约定定理包括：对于一个四边形，如果一对对边互相平行且相等，则该四边形是一个平行四边形。

这一定理是在已知对边平行且相等的情况下，判定四边形为平行四边形的准则。

3. 平行四边形的对角线定理平行四边形的对角线定理包括：在平行四边形中，对角线互相平分并且对角线之间线段成比例。

这一定理在解析几何的证明中经常被使用，帮助推导其他几何图形的性质。

四、应用举例平行四边形的特性和定理在解析几何中有许多具体的应用。

其中一些应用包括：1. 确定平行四边形通过判断四边形的对边是否平行且相等，可以确定一个四边形是否为平行四边形。

这对于解决几何问题和证明几何定理十分重要。

2. 求解平行四边形的性质通过运用平行四边形的特性和定理，可以求解平行四边形的内角、对角线长度等性质。

初中几何基本图形归纳(基本图形+常考图形)初中几何常见基本图形1.基本图形及结论A、B、C、D分别为四边形的顶点，AC=BD，AD=BC，∠AOC=∠BOD，∠AOD=∠BOC。

2.直角三角形在直角三角形ABC中，∠C=90°，OA为斜边的中线，OD⊥XXX。

3.等腰三角形在等腰三角形ABC中，AB=AC，AD为角A的平分线，BD=CD。

4.三角形的面积公式在三角形ABC中，AB2=BD×BC，AC2=CD×BC。

5.三角形内角和公式在三角形ABC中，∠A+∠B+∠C=180°。

6.平行四边形在平行四边形ABCD中，∠A+∠B=∠C+∠D，AC平分∠BAD。

7.直角三角形的斜边中线在直角三角形ABC中，BD为斜边AC的中线，∠B=∠D。

8.直角三角形的高线在直角三角形ABC中，PA⊥AB，PB⊥AC，PC⊥BC，且PA=PB+PC，∠P=∠A/2.9.直角三角形的内心在直角三角形ABC中，∠P=∠A/2，PD为角A的平分线，AD=BD=AC=DC。

10.直角三角形的外心在直角三角形ABC中，∠P=90°-∠A/2，以AB的中点O为圆心，AB为半径作圆，交AC于点P，则P为三角形ABC的外心。

11.等腰三角形的中线在等腰三角形ABC中，AB=CB，BD为角B的平分线，且BC∥AD。

12.等边三角形在等边三角形ABC中，AB=AC=BC。

13.等角三角形在等角三角形ABC中，∠A=∠B=∠C。

14.三角形的相似在三角形ABC和DEF中，如果∠A=∠D，∠B=∠E，∠C=∠F，则称三角形ABC与DEF相似。

15.圆的基本性质在圆O中，AB为直径，则∠C=90°，且AC=BC=OD。

16.圆的切线在圆O中，以点A为圆心，AB为半径作圆，则CD为圆O的切线。

17.圆的割线在圆O中，以点A为圆心，AC为半径作圆，则BD为圆O的割线。

18.圆的弦在圆O中，AB为圆O的弦，R为圆O的半径，则弦长公式为AB2=BD×BC，且弦AB平分∠AOB。

四边形的分类与性质四边形是几何中最基本的多边形之一，由四条线段组成。

它是日常生活中常见的图形，具有不同的分类和特征。

本文将对四边形的分类和性质进行详细阐述，以帮助读者更好地理解和应用于实际问题中。

一、四边形的分类四边形可以根据其边长、角度以及对角线等特征进行分类。

下面将介绍几种常见的四边形分类：1.平行四边形平行四边形是指具有对边平行的四边形。

它的特征是相对的两边和对角线的长度相等，相邻的两个角也相等。

平行四边形可以进一步分为矩形、正方形和菱形。

2.矩形矩形是具有四个直角的平行四边形。

它的特点是两对对边相等且平行，对角线的长度相等。

矩形的性质还包括相邻角互补，对角线相互垂直等。

3.正方形正方形是一种特殊的矩形，它有四个相等的边和四个相等的直角。

正方形的对角线相互垂直且长度相等。

正方形的性质还包括对角线平分内外角等。

4.菱形菱形是具有四个边长相等的平行四边形。

它的特点是对角线互相垂直且长度相等。

菱形的性质还包括相邻角互补，对边平分内外角等。

5.梯形梯形是指至少有一对对边是平行的四边形。

根据其两边的长度关系，梯形可以分为等腰梯形和不等腰梯形。

梯形的性质还包括对角线的长度关系以及内角和外角之和等。

二、四边形的性质除了不同种类的四边形具有各自独特的性质外，还存在一些普遍适用于所有四边形的性质。

以下是几个常见的四边形性质：1.内角和任意四边形的内角和等于360度。

这意味着四边形的四个内角之和始终等于这个固定值。

2.对边关系在平行四边形中，对边相等且平行。

对角线将平行四边形分为两个相等的三角形。

3.对角线关系任意四边形的对角线将其分为两个相等的三角形。

这些三角形可能是等边、等腰或一般三角形。

4.面积计算可以通过不同的方法计算四边形的面积。

例如，矩形和正方形的面积可以通过长度和宽度的乘积计算，菱形的面积可以通过对角线长度的乘积再除以2计算。

三、应用实例四边形的分类和性质在实际生活和工作中有广泛的应用。

以下是几个例子：1.建筑设计建筑师需要了解不同种类的四边形，如平行四边形、矩形和正方形等。

四边形基本图形知识点总结四边形是几何学中常见的图形，它有许多重要的性质和知识点。

本文将带您深入了解四边形的基本概念、分类和特性。

一、四边形的基本概念四边形是指具有四条边的图形。

它是多边形的一种特殊情况，由四个顶点和四条边构成。

尽管四边形是一个广义的概念，但在几何学中我们通常讨论的是平面四边形。

二、四边形的分类根据四边形的性质，我们可以将其分类为以下几种常见类型：1.矩形：四个角都是直角的四边形。

矩形的对边相等且平行。

2.正方形：具有四个相等边长和四个直角的矩形。

3.平行四边形：有两组对边分别平行的四边形。

4.梯形：有一对对边平行的四边形。

5.菱形：四个边长相等的梯形。

6.不规则四边形：没有对边平行或边长相等的四边形。

三、四边形的性质和特性1.内角和：四边形的内角和等于360度。

2.外角和：四边形的外角和等于360度。

3.对角线：四边形的对角线是相邻顶点之间的直线段。

对角线有以下重要性质：–矩形的对角线相等；–平行四边形的对角线互相平分；–菱形的对角线互相垂直且平分；–梯形的对角线不相交。

4.邻边和对边：在平行四边形中，邻边是指两个相邻的边，对边是指不相邻但平行的边。

在矩形和正方形中，邻边和对边是相同的。

5.矩形和正方形的特性：–矩形的对边相等且平行；–矩形的对角线相等；–正方形是一种特殊的矩形，具有四个相等的边长和四个直角。

四、四边形的计算在解决与四边形相关的问题时，我们经常需要计算其面积和周长。

下面是一些常见四边形的计算公式：1.矩形的面积为长度乘以宽度，周长为两倍长度加两倍宽度。

2.正方形的面积为边长的平方，周长为四倍边长。

3.平行四边形的面积为底边乘以高，周长为两倍底边加两倍高。

4.梯形的面积为上底加下底乘以高的一半，周长为所有边长之和。

五、应用实例四边形的概念和性质在日常生活和工作中都有广泛的应用。

例如：1.建筑设计：在建筑设计中，矩形和正方形的特性被广泛应用于房屋的布局和结构设计。

2.地理测量：平行四边形的特性可用于测量地块面积或河流的宽度。

平行四边形底和高的长度关系一、概述平行四边形是一种基本的几何图形，其底和高的长度关系是几何学中的一个重要知识点。

本文将从定义、性质和应用三个方面，全面阐述平行四边形底和高的长度关系。

二、定义平行四边形是指有两对对边分别平行的四边形。

在平行四边形中，底是指两个相邻且平行的边中的任意一个，高则是指从该底所在点到与另一条底垂直且在同一水平线上的线段长度。

三、性质1. 平行四边形底和高互相垂直。

证明：设ABCD为平行四边形，以AB为底，EF为高，则由定义可知EF与AB垂直。

又因为AD∥BC，所以∠EAF=∠EDC（同旁内角），而∠EAF+∠EDF=180°（EF为直线），因此∠EDF=90°，即EF与DC垂直。

因此，在任意一个平行四边形中，底和高互相垂直。

2. 平行四边形底和高之间存在等比例关系。

证明：设ABCD为平行四边形，以AB为底，EF为高，则由定义可知EF与AB垂直。

设EF=x，AD=h，则由三角形相似可得：EF/AD=AB/DC即x/h=AB/DC因此，平行四边形底和高之间存在等比例关系。

3. 平行四边形底和高的长度关系为：面积=底×高。

证明：设ABCD为平行四边形，以AB为底，EF为高，则由定义可知EF与AB垂直。

设AB=a，AD=b，则平行四边形的面积为：S=EF×AB=(a×h)/2又因为h=2S/b，所以：S=(a×h)/2=(a×2S/b)/2=aS/b因此，平行四边形底和高的长度关系为：面积=底×高。

四、应用1. 计算平行四边形的面积。

根据性质3可知，在已知平行四边形的底和高的长度时，可以直接用公式S=底×高计算其面积。

例如，在一个平行四边形中，底长为8cm，高长为5cm，则其面积为40cm²。

2. 判断图形是否是平行四边形。

根据定义可知，在一个图形中如果有两对对边分别平行，则该图形是一个平行四边形。

四年级数学奥数培优练习第11讲：四边形中的基本图形（一）通用版（含答案）x一．夯实基础：1.在平行四边形ABCD 中, E 为BC 上的任意点,且S AED =10 ,求平行四边形的面积是多少？2.在平行四边形ABCD 中, E 为BC 上的任意点,且S AEB +S CED =15 ,求平行四边形的面积是多少？BD C3.在平行四边形中,阴影部分的面积和是12,求平行四边形的面积是多少？1 / 10平方厘米,小正方形的面积为9 平方厘米,求图中一个长方形的面积是多少？4.如图,ABFE 和CDEF 都是长方形,AB 的长是4 厘米,BC 的长是3 厘米．那么图中阴影部分的面积是多少？5.如图,小、中、大三个正方形从左到右依次紧挨着摆放,边长分别是3、7、9。

图中两个阴影平行四边形的面积分别是多少？2 / 106.如图是一块长方形草坪,中间有两条道路,路宽是2 米,求有草部分的面积．二．拓展提高：7.如图,矩形DEFG 的宽DE = 4 厘米,长DG = 4DE , 则正方形ABCD 的边长是多少厘米?3 / 108.如图是一块正方形草坪,中间有三条道路,路宽是2 米,求有草部分的面积．9.如图,在平行四边形ABCD 中,三角形BCE 的面积是42 平方厘米,BC 的长度为14 厘米,AE 的长度为9 厘米,那么平行四边形ABCD 的面积是多少平方厘米？三角形ECD 的面积又是多少平方厘米？4 / 1010.四年级数学奥数培优练习第11讲：四边形中的基本图形（一）通用版（含答案）xA BD E C11.如图,正方形被分成9个小长方形,其中5 个小长方形的面积如图所示,求其它4 个小长方形的面积.12.如图,校园中间有个正方形花坛,花坛的四周铺了1 米宽的水泥路。

如果水泥路的总面积是24 平方米,那么花坛的面积是多少平方米？5 / 1013.如图,正方形ABCD 的边长是4 厘米,矩形DEFG 的长DG = 5 厘米,求它的宽DE = ?EA DFB G C14.如图, ABCD 是一个长方形, E 点在CD 延长线上．已知AB = 5 ,BC =12 ,且三角形AFE 的面积等于20,那么三角形CFE 的面积等于多少？EA DB C15.如图,边长为10 的正方形中有一等宽的十字,其面积（阴影部分）为36 ,则十字中央的小正方形面积为．6 / 1019.（迎春杯）右图中平行四边形的面积是1080m2,则平行四边形的周长为m。

平行四边形的命名点顺序平行四边形是一种基本的几何形状，具有四个顶点、四条边和两个对角线。

本文将介绍平行四边形的命名点顺序，主要包括顶点、边、对角线、面积和形状等方面。

1. 顶点平行四边形的四个顶点可以按照以下顺序进行命名：1. 顶点1：位于平行四边形的左上角。

2. 顶点2：位于平行四边形的左下角。

3. 顶点3：位于平行四边形的右下角。

4. 顶点4：位于平行四边形的右上角。

在许多几何问题中，正确识别和命名顶点是非常重要的，因为它们通常涉及到图形的对称性、全等关系以及角度和边长等量的计算。

2. 边平行四边形有四条边，它们两两平行，且长度相等。

按照顺时针方向，可以将这四条边命名为：1. 边1：连接顶点1和顶点3。

2. 边2：连接顶点2和顶点4。

3. 边3：连接顶点1和顶点4。

4. 边4：连接顶点2和顶点3。

在一些问题中，需要对边进行测量或者比较其长度。

边长可以根据需要计算，例如通过勾股定理或者使用相似三角形的比例关系等。

3. 对角线平行四边形有两个对角线，它们将平行四边形分成两个全等的三角形。

按照顺时针方向，可以将这两条对角线命名为：1. 对角线1：连接顶点1和顶点4。

2. 对角线2：连接顶点2和顶点3。

对角线的长度可以通过三角形的两边长度进行计算，也可以使用勾股定理等几何定理进行求解。

另外，对角线的角度也是一些问题中需要关注的量。

4. 面积平行四边形的面积可以通过以下公式计算：面积= 底边长度×高。

这是因为平行四边形可以被看作是由一个矩形去掉一个与其底边长度和高分别相等的三角形所得到。

根据这个公式，可以方便地求出平行四边形的面积。

例如，如果已知平行四边形底边长度为10，高为5，则其面积为：10 ×5 = 50。

5. 形状平行四边形是一种凸形，即所有顶点都在一个平面内，并且任意两边所在直线都相交于一点。

根据定义，一个平行四边形有两组相等的对角，即对角线将平行四边形分成两个全等的三角形。

第十八章平行四边形知识点总结
一 基本概念：四边形，四边形的内角，四边形的外角，多边形，平行线间的距离，平行四
边形，矩形，菱形，正方形，中心对称，中心对称图形，梯形，等腰梯形，直角梯形，三角形中位线，梯形中位线. 二 定理：中心对称的有关定理
※1．关于中心对称的两个图形是全等形.
※2．关于中心对称的两个图形，对称点连线都经过对称中心，并且被对称中心平分.
※3．如果两个图形的对应点连线都经过某一点，并且被这一点平分，那么这两个图形关于
这一点对称. 三 公式：
1．S 菱形 =2
1
ab=ch.（a 、b 为菱形的对角线 ,c 为菱形的边长 ，h 为c 边上的高） 2．S 平行四边形 =ah. a 为平行四边形的边，h 为a 上的高） 3．S 梯形 =2
1
（a+b ）h=Lh.（a 、b 为梯形的底，h 为梯形的高,L 为梯形的中位线） 四 常识：
※1．若n 是多边形的边数，则对角线条数公式是：2
)3n (n -. 2．规则图形折叠一般“出一对全等，一对相似”.
3．如图：平行四边形、矩形、菱形、正方形的从属关系.
4．常见图形中，仅是轴对称图形的有：角、等腰三角形、等边三角形、正奇边形、等腰梯形 …… ；仅是中心对称图形的有：平行四边形 …… ；是双对称图形的有：线段、矩形、菱形、正方形、正偶边形、圆 …… .注意：线段有两条对称轴.
平行四边形
矩形
菱形正
方
形。

三平行四边形、梯形和三角形一、平行四边形1.平行四边形的定义。

两组对边分别平行的四边形叫作平行四边形。

2.平行四边形的基本特征。

平行四边形的两组对边分别平行且相等。

3.长方形、正方形和平行四边形之间的关系。

长方形和正方形同平行四边形一样,都是两组对边分别平行且相等,长方形和正方形具有平行四边形的一切特征,所以长方形和正方形都是特殊的平行四边形。

正方形不仅具备长方形的所有特征,并且四条边都相等,所以正方形是特殊的长方形。

4.平行四边形的特性。

平行四边形具有不稳定性,容易变形。

5.平行四边形的面积。

(1)认识平行四边形的底和高。

从平行四边形一条边上的任意一点向对边引垂线,这点到垂足间的线段叫作平行四边形的高,垂足所在的边叫作平行四边形的底。

平行四边形有无数条高,一般能画出两种长度的高。

(2)平行四边形的面积。

通过剪拼发现:长方形的面积与平行四边形的面积相等,平．重点提示:在拉动长方形的过程中,长方形的形状改变,但两组对边的长度不变。

易错题:平行四边形的对边一定相等,邻边一定不相等。

( )错解分析:此题错在对平行四边形的特征理解不准确,平行四边形一定具备对边相等的特征,但对邻边没有要求,所以平行四边形的邻边也可以相等。

正确答案:✕重点提示:平行四边形的底和高是一组相互依存且对应的概念(底边上的高,高所对应的底)。

易错题:周长相等的两行四边形的底等于长方形的长．．．．．．．．．．．．．;．平行四边形的高等于长方形的．．．．．．．．．．．．．宽．。

长方形的面积=长×宽平行四边形的面积=底×高如果用S表示平行四边形的面积,a和h分别表示平行四边形的底和高,那么平行四边形的面积的字母公式为S=ah。

二、梯形1.梯形的定义。

只有一组对边平行的四边形叫作梯形。

2.平行四边形和梯形的异同点。

相同点:都是四边形;都有平行的对边。

不同点:平行四边形的两组对边分别平行且相等;梯形只有一组对边平行,且平行的这组对边不相等。

特殊的平⾏四边形专题（题型详细分类）要点特殊的平⾏四边形讲义知识点归纳矩形，菱形和正⽅形之间的联系如下表所⽰：四边形分类专题汇总专题⼀：特殊四边形的判定矩形菱形正⽅形性质边对边平⾏且相等对边平⾏，四边相等对边平⾏，四边相等⾓四个⾓都是直⾓对⾓相等四个⾓都是直⾓对⾓线互相平分且相等互相垂直平分，且每条对⾓线平分⼀组对⾓互相垂直平分且相等,每条对⾓线平分⼀组对⾓判定 ·有三个⾓是直⾓; ·是平⾏四边形且有⼀个⾓是直⾓; ·是平⾏四边形且两条对⾓线相等. ·四边相等的四边形；·是平⾏四边形且有⼀组邻边相等；·是平⾏四边形且两条对⾓线互相垂直。

·是矩形，且有⼀组邻边相等； ·是菱形，且有⼀个⾓是直⾓。

对称性既是轴对称图形，⼜是中⼼对称图形（1）______________ （2）______________ （3）______________ （4）______________ （5）______________2.矩形的判定⽅法：（1）______________ （2）______________ （3）______________3.菱形的判定⽅法：（1）______________ （2）______________ （3）______________4.正⽅形的判定⽅法：（1）______________ （2）______________ （3）______________5.等腰梯形的判定⽅法：（1）______________ （2）______________ （3）______________【练⼀练】⼀．选择题1．能够判定四边形ABCD是平⾏四边形的题设是（）．A．AB∥CD，AD=BC B．∠A=∠B，∠C=∠DC．AB=CD，AD=BC D．AB=AD，CB=CD2．具备下列条件的四边形中，不能确定是平⾏四边形的为（）．A．相邻的⾓互补 B．两组对⾓分别相等C．⼀组对边平⾏，另⼀组对边相等 D．对⾓线交点是两对⾓线中点3.下列条件中，能判定四边形是平⾏四边形的条件是( )A.⼀组对边平⾏，另⼀组对边相等B.⼀组对边平⾏，⼀组对⾓相等C.⼀组对边平⾏，⼀组邻⾓互补D.⼀组对边相等，⼀组邻⾓相等4．如下左图所⽰，四边形ABCD的对⾓线AC和BD相交于点O，下列判断正确的是（）．A．若AO=OC，则ABCD是平⾏四边形;B．若AC=BD，则ABCD是平⾏四边形;C．若AO=BO，CO=DO，则ABCD是平⾏四边形;D．若AO=OC，BO=OD，则ABCD是平⾏四边形5．不能判定四边形ABCD是平⾏四边形的条件是（）A．AB=CD，AD=BC B．AB∥CD，AB=CDC．AB=CD，AD∥BC D．AB∥CD，AD∥BC6.四边形ABCD的对⾓线AC，BD相交于点O，能判断它为矩形的题设是（）A．AO=CO，BO=DO B．AO=BO=CO=DOC．AB=BC，AO=CO D．AO=CO，BO=DO，AC⊥BD7.四边形ABCD的对⾓线互相平分，要使它变为矩形，需要添加的条件是（）A．AB=CD B．AD=BC C．AB=BC D．AC=BD8.在四边形ABCD中，O是对⾓线的交点，下列条件能判定这个四边形是正⽅形的是（）A、AC＝BD，AB∥CD，AB＝CDB、AD∥BC，∠A＝∠CC、AO＝BO＝CO＝DO，AC⊥BDD、AC＝CO，BO＝DO，AB＝BC9.在下列命题中，真命题是（）Ａ．两条对⾓线相等的四边形是矩形Ｂ．两条对⾓线互相垂直的四边形是菱形Ｃ．两条对⾓线互相平分的四边形是平⾏四边形Ｄ．两条对⾓线互相垂直且相等的四边形是正⽅形10.在下列命题中，正确的是（）11.如图，已知四边形ABCD 是平⾏四边形，下列结论中不正确的是（） A ．当AB=BC 时，它是菱形 B ．当AC ⊥BD 时，它是菱形C ．当∠ABC=900时，它是矩形D ．当AC=BD 时，它是正⽅形12.如图，在ABC △中，点E D F ，，分别在边AB ，BC ，CA 上，且DE CA ∥，DF BA ∥．下列四个判断中，不正确．．．的是（） A ．四边形AEDF 是平⾏四边形B ．如果90BAC ∠=o ，那么四边形AEDF 是矩形C ．如果AD 平分BAC ∠，那么四边形AEDF 是菱形D ．如果AD BC ⊥且AB AC =，那么四边形AEDF 是菱形 13.下列条件中不能判定四边形是正⽅形的条件是（）。

个人收集整理-仅供参考15 / 11 第二单元 平行四边形的初步认识单元教材分析：《认识平行四边形》是小学数学二年级上册的教学内容。

本课的教学内容是在学生已经学习了多边形的基本知识，系统的认识了平行四边形，同时又为以后学习相关图形的面积计算做准备。

为了使学生对平行四边形的不稳定性有清晰的认识。

我为学生准备了两个框架，一个是平行四边形，另一个是三角形。

我让学生先猜测“如果用力拉这两个框架，哪一个的形状更容易发生变化。

”再请一位力气大的学生拉三角形，一位力气小的同学拉平行四边形。

让学生通过猜测和对比鲜明的实际动手验证，对平行四边形的不稳定性有直观的认识。

然后，我问：“通过对刚才活动的观察，你们有什么想要说的吗？”通过小组及全班的交流，学生在已经认识的三角形稳定性的基础上认识了平行四边形的不稳定性。

从而在操作中培养了学生的猜测、动手验证、知识间的比较、归纳的能力。

单元教学内容：义务教育课程标准实验教科书二年级（上册）第—页。

单元教学目标：．使学生通过观察、操作、比较和交流，初步认识四边形、五边形、六边形，以及平行四边形等平面图形，知道这些图形的名称，能正确识别这些图形；初步了解平行四边形在日常生活中的应用。

．使学生在折、剪、拼等活动中，初步体会相关平面图形之间的联系，发展初步的空间观念。

．使学生在认识图形的过程中，进一步产生对数学学习的兴趣和自信心，培养主动与同伴合作、交流的意识。

单元教学重难点：重点是让学生联系生活实际，通过动手操作，在“做”平行四边形的过程中，认识平行四边形。

难点是让学生通过图形变换体会有关平面图形的特征，感受不同平面图形之间的联系与区别，并通过开放性的问题激活学生的发散性思维。

单元课时安排：课时第一课时 认识多边形教学内容：苏教版二年级上册第～页例和“想想做做”第～题。

教学目标：．使学生通过观察、比较、分类，认识四边形、五边形、六边形等平面图形，能判断一个由线段围成的图形是几边形，能按要求围出或剪出多边形。

小学数学认识正方形长方形和平行四边形数学是小学阶段非常重要的一门学科，其中正方形、长方形和平行四边形是非常基础也非常重要的几何图形。

本文将详细介绍这几种图形的定义、性质以及与其他图形的比较。

一、正方形正方形是一种特殊的四边形，具有以下性质：1. 所有边的长度相等；2. 每个角都是90度；3. 对角线相等且互相垂直。

正方形广泛应用于生活和工作中，例如瓷砖、电视机、电脑屏幕等。

其特点是形状规则，四个角都是直角，相邻边相互垂直。

在计算正方形的面积时，只需将边长平方即可。

二、长方形长方形也是一种特殊的四边形，具有以下性质：1. 两对边相互平行；2. 相对的两边长度相等；3. 每个角都是90度。

长方形常见于我们生活中，例如门、书桌、窗户等。

它是最基本的矩形，具有两对平行边和四个直角。

计算长方形的面积时，只需将长乘以宽即可。

三、平行四边形平行四边形是指具有以下性质的四边形：1. 对边两两平行；2. 两对边长度分别相等。

平行四边形在建筑物、工程设计和几何推理中都有广泛应用。

它与长方形和正方形的区别在于不一定有直角。

对于平行四边形，计算面积的公式为底乘以高。

以上是对小学数学中常见的正方形、长方形和平行四边形的介绍。

通过学习和了解这些图形的定义和性质，可以帮助学生更好地理解几何形状的特点和计算方法。

同时，通过与其他图形的比较，可以更深入地理解它们之间的差异。

例如，正方形和长方形都是特殊的平行四边形，但正方形的特点是所有边和角均相等，而长方形的特点是只有相对的两边和四个角是相等的。

此外，正方形和长方形还有一些相似之处。

它们的对角线都相等且互相垂直，面积计算公式也都是边长的相乘。

无论是正方形、长方形还是平行四边形，它们都是几何图形中的基础，并在日常生活和学习中起着重要的作用。

通过深入学习和理解这些图形的定义、性质和计算方法，可以为小学生打下坚实的数学基础，为更高级的几何学习做好准备。

综上所述，正方形、长方形和平行四边形是小学数学中非常重要的三个几何图形。

长方形与平行四边形的关系
长方形与平行四边形是几何图形中的两种基本图形，它们之间有着千丝万缕的联系。

首先，从概念上讲，长方形是一种四边形，它由四条相等的直角线组成，四个角等于90度，它有四条对称轴，两个主
对角线，对边相等。

而平行四边形也是一种四边形，它有四条平行边，四个角等于360度，它没有对称轴，两个主对角线也不相等。

其次，从几何性质来看，长方形和平行四边形都是平行四边形，具有相同的角度和边长。

但它们之间有一个重要的区别，就是长方形有对称轴，而平行四边形没有。

因此，在旋转长方形时，可以得到一个平行四边形，而旋转平行四边形则不能得到长方形。

此外，长方形和平行四边形在几何中都有着重要的作用，它们都是几何图形的基本形状，可以用来构建更复杂的几何图形，如三角形，矩形，圆形等。

最后，长方形和平行四边形之间的关系可以总结为：长方形是一种四边形，它具有相同的角度和边长，但有四条对称轴；而平行四边形没有对称轴，旋转长方形可以得到一个平行四边形，但旋转平行四边形则不能得到长方形。

总之，长方形和平行四边形在几何中有着千丝万缕的联系，它们是几何图形的基本图形，可以用来构建更复杂的图形，如三角形，矩形，圆形等。

因此，长方形和平行四边形之间的关系是非常重要的，在研究几何中也不可忽视这一关系。

平面图形中平行四边形的分类及作图教案。

一、平行四边形的分类平面图形中的平行四边形，根据它的不同性质和形态可以分为以下几种类型：1.等腰平行四边形：如果平行四边形的两对相邻边相等，则称之为等腰平行四边形。

在等腰平行四边形中，对角线互相平分。

2.矩形：如果平行四边形的四个角都是直角，则称之为矩形。

在矩形中，对角线互相相等。

3.正方形：如果平行四边形既是矩形，又是等腰平行四边形，则称之为正方形。

在正方形中，对角线互相相等且垂直，对边互相平行且相等。

4.菱形：如果平行四边形的四个边都相等，则称之为菱形。

在菱形中，对角线互相平分且垂直。

5.斜四边形：如果平行四边形的相邻两边不相等，则称之为斜四边形。

二、平行四边形的绘制在平面图形的绘制中，平行四边形也占有重要的位置。

下面是平行四边形的绘制方法：1.以一直线段为基础，向两侧分别画出两条和它平行的线段。

2.用尺子测量两条平行线段之间的距离，然后用这个距离在两侧平行线段上分别找出一个等距离的点，用直尺连接两个点，即可得出平行四边形。

3.如果要绘制特殊形态的平行四边形，可以按照其特定的条件进行绘制。

例如，要绘制等腰平行四边形，则需要先绘制出两个等边的直角三角形，然后根据其特殊条件进行相应的加工。

三、平行四边形的基本性质平行四边形具有许多重要的性质，在学习平行四边形时，需要对这些性质进行深入地理解和掌握。

下面是平行四边形的几个基本性质：1.平行四边形的相邻的两个内角互补。

2.平行四边形的对角线互相平分。

3.对于等腰平行四边形，对角线互相垂直。

4.对于矩形和正方形，对角线互相相等且垂直。

5.对于正方形，对边互相平行且相等。

6.平行四边形的面积等于底边长乘以高。

四、平行四边形的应用平行四边形是数学学科中具有广泛应用的基础形态之一，在许多实际问题中都有其重要的应用。

平行四边形的应用包括以下几个方面：1.平行四边形的面积计算：平行四边形的面积计算是其在实际应用中被广泛使用的一个方面。