4.1.2用字母表示数量关系练习题及答案

易错题:填空:张师傅每天加工a个零件,3天加工(3+a)个。

错因分析:此题错在没有正确理解题中的数量关系。

每天加工a个零件,3天就加工(a+a+ a)个,求3个a相加的和是多少,用乘法计算,列式为3a。

正确答案:3a易错提示:当两个数相乘时，乘号不能省略。

知识巧记:字母表数很重要,生活当中离不了。

写进式子本领大,合理数据都可表,数据如若有一定,代入式子值求到。

乘法式子能简写,乘号写点或省掉。

要点提示:1.a2表示2个a相乘,2a表示2个a相加。

2.相同的字母在不同的式子中表示的意义不一定相同。

知识拓展:若干个数相加,任意交换加数的位置,它们的和不变。

第1课时用字母表示数1. 一名健康儿童平均每分钟的心跳为a次，健康儿童每小时的心跳为次。

2.小亮比小强大2岁，比小花小4岁，如果小强是m岁，小花是（）岁．A．m-2 B.m+4 C．m+63.一件衣服X元，比一条裤子的2倍还少30元．一条裤子（）元．A．2X-30 B．（X+30）÷2 C．（X-30）÷2答案1.60a2.C3.B第2课时用字母表示公式3.说说下面式子表示的含义.同学们去电影院看电影，前二十排平均每排坐x人，后十排平均每排坐y人。

（1）20x（2）20x+10y（3）20x-10y答案1. C=4a S=a22. C=（a+b）×2 S=a×b3.（1）20x表示前二十排的总人数；（2）20x+10y表示电影院一共坐的人数；（3）20x-10y表示前二十排的人数比后十排多坐的人数.第3课时用字母表示加法运算定律1.通过所学，完成下表。

2.用字母表示加法交换律，错误的是（）A．a+b=b+a B．m+n=n+m C．p×q=q×p3.判断题.用字母表示加法交换律是a+b=b+a，长方形面积公式是s=ab，这两个公式中的a，b表示的意思是一样的.（）答案2. C3.×第二单元测试卷一、填空：（1×20=20分）1、学校有图书400本，又买来ａ本，现在一共有（）本。

龙文教育学科教师辅导讲义课 题4.1-2用字母表示数及代数式教学目标1、明确用字母表示数的意义及会用字母表示数；2.会列代数式表示简单的数量关系，会正确书写代数式，会求代数式的值.3.在数学活动中，体会抽象概括的数学思想方法和“特殊 一般”相互转化的辨证关系.重点、难点理解字母所代表数的范围。

考点及考试要求教学内容知识梳理1. 代数式：用运算符号“＋ － × ÷ …… ”连接数及表示数的字母的式子称为代数式.注意：用字母表示数有一定的限制，首先字母所取得数应保证它所在的式子有意义，其次字母所取得数还应使实际生活或生产有意义；单独一个数或一个字母也是代数式；用基本运算符号把数和字母连接而成的式子叫做代数式，如n,-1,2n+500,abc 。

2. 代数式书写规范：（1）数与字母相乘，或字母与字母相乘中通常使用“· ” 乘，或省略不写； （2）数与数相乘，仍应使用“×”乘，不用“· ”乘，也不能省略乘号； （3）数与字母相乘时，一般在结果中把数写在字母前面，如a ×5应写成5a ； （4）带分数与字母相乘时，要把带分数改成假分数形式，如a ×211应写成23a ；（5）在代数式中出现除法运算时，一般用分数线将被除式和除式联系，如3÷a 写成a3的形式；（6）a 与b 的差写作a-b ，要注意字母顺序；若只说两数的差，当分别设两数为a 、b 时，则应分类，写做a-b 和b-a .出现除式时，用分数表示；(7)若运算结果为加减的式子，当后面有单位时，要用括号把整个式子括起来。

3.几个重要的代数式：（m 、n 表示整数）（1）a 与b 的平方差是： a 2-b 2 ； a 与b 差的平方是：（a-b ）2 ；（2）若a 、b 、c 是正整数，则两位整数是： 10a+b ,则三位整数是：100a+10b+c ；（3）若m 、n 是整数，则被5除商m 余n 的数是： 5m+n ；偶数是：2n ，奇数是：2n+1；三个连续整数是： n-1、n 、n+1 ；（4）若b ＞0，则正数是:a 2+b ，负数是： -a 2-b ，非负数是： a 2，非正数是：-a 2.典型例题例1 某市出租车收费标准为：起步价5元，3千米后每千米价1.2元，则乘坐出租车走x(x ﹥3)千米应付______________元.分析：因为x ﹥3，所以应付费用分为两部分，一部分为起步价5元，另一部分为走（x-3）千米应付的1.2（x-3）元. 解：[])3(2.15-+x注意：和、差形式的代数式要在单位前把代数式括起来. 例2 下列代数式中，书写正确的是（ ）A. ab ·2B. a ÷4C. -4×a ×bD.xy213 E.mn35 F. -3×6分析：A ：数字应写在字母前面 B ：应写成分数形式，不用“÷”号 C ：数与字母相乘，字母与字母相乘时，“×”号省略 D ：带分数要写成假分数 E 、F 书写正确. 解：E 、F.例3 下列各题中，错误的是（ ） A. 代数式.,22的平方和的意义是y x y x +B. 代数式5(x+y)的意义是5与(x+y)的积C. x 的5倍与y 的和的一半，用代数式表示为25y x +D. 比x 的2倍多3的数，用代数式表示为2x+3 分析：选项C 中运算顺序表达错误，应写成)5(21y x +友情提示：数学语言有文字语言、符号语言、图形语言.进行数学思维时，同学们要学会恰当使用各种语言推理分析，各种语言的互译是一种数学基本功. 例4 当x=1时，代数式13++qx px 的值为2005，求x=－1时，代数式13++qx px 的值.分析：当x=1时，13++qxpx ==++1q p 2005，p+q=2004,当x=－1时，13++qx px =－=+-1q p －（p+q ）+1=－2004+1=－2003.解：当x=1时，13++qxpx ==++1q p 2005∴ p+q=2004∴当x=－1时，13++qxpx =－1+-q p=－（p+q ）+1=－2004+1 =－2003.提示：“整体”思想在数学解题中经常用到，请同学们在解题时恰当使用.例5 下图是一个数值转换机的示意图，请你用x 、y 表示输出结果，并求输入x 的值为3，y 的值为-2时的输出结果. 解：输出结果用x 、y 表示为：223yx +当x=3,y=-2时,223yx +=2)2(323-+⨯=-1.提示：把图形语言翻译为符号语言的关键是识图， 弄清图中运算顺序.例6 某餐饮公司为大庆路沿街20户居民提供早餐方便，决定在路旁建立一个快餐店P ，点P 选在何处，才能使这20户居民到P 点的距离总和最小？输入x 输入y×2( )3+÷2输出结果分析：面对复杂的问题，应先把问题“退”到比较简单的情形：如图1，如果沿街有2户居民，很明显点P 设在p 1、、、p 2之间的任何地方都行.如图2，如果沿街有3户居民， 点P 应设在中间那户居民、p 2门前.------以此类推，沿街有4户居民，点P 应设在第2、3户居民之间的任何位置，沿街有5户居民，点P 应设在的第3户门前，------沿街有n 户居民：当n 为偶数时，点P 应设在第2n 、12+n 户居民之间的任何位置；当n 为奇数时，点P 应设在第21+n 户门前.解：根据以上分析，当n=20时，点P 应设在第10、11户居民之间的任何位置. 思维驿站： 请同学们认真体会“特殊⇔一般”的辨证关系，掌握化归的思想方法，学会把复杂的问题化为简单的情形来解决.二、点将练兵训练一一、 选择题 1、 在式子x+2,3a2b,m,S=,2Rπc b a yx 2,3>+-中代数式有（）A 、6个B 、5个C 、4个D 、3个. p 1. p .p 2图1.p 1、 .p 2（p ） .p 3图22、 下列式子中符合书写要求的是（）A 、42ba B 、abc 312 C 、cb a ÷⨯ D 、ayz33、 一件衣服降价10%后卖a 元，则原则是（）A 、10xB 、x 910 C 、x 101 D 、x10094、 用代数式表示“a ，b 两数的和与c 的积是”（）A 、a 十bcB 、ab 十cC 、（a 十b ）cD 、a （b 十c ） 5、甲数为a ，乙数为b ，甲数的32 与乙数的倒数差是（）A 、ba 132- B 、b a -23C 、ba 132+D 、b a +236、大连向北京打长途电话，通话费3分钟以内3.6元，每超过1分钟加收1元钱，某人打电话x 分钟（x>3的整数），则应付话费（）元A 、3.6xB 、3.6+xC 、0.6+xD 、x 一3.6 7、代数式ba12-的正确解释是（）A 、 a 与b 的倒数的差的平方B 、 a 与b 的差的平方的倒数C 、 a 的平方与b 的差的倒数D 、 a 的平方与b 的倒数的差8、长方形的长是宽的1.6倍，则宽为12厘米时，其周长L 的值是（） A 、62.4厘米 B 、31.2厘米 C 、27.2厘米 D 19.8厘米 二、 填空题1、a 、b 两数的平方和，其代数式表示为2、比a 、b 两数的差的3倍大c 的数是3、一种商品是m 元，则涨价15%以后的售价是4、当x=1，y=2时，代数式y x 214 的值是5、当n 为自然数，则任何一个偶数可表示为6、某人存入银行a 元，设年利率为x ，若扣除税b 元，则一年后取回本息共 元。

《用字母表示数量及数量关系》常见精选练习题一、填空题。

1、阳光图书室有图书4000本，又买来X本，现在一共有( )本。

2、找规律，看看字母代表的是什么数。

1、3、5、a、9、11、13 a=（）5、10、15、b、25、30 b=（）99、88、c、66、55 c=( )1、2、4、7、11、X、22 X=( )3、用数是3.5比乙数多a乙数是用乙两数和是（）4、一个等边三角形，每边长 a米。

它的周长是( )米。

5、一辆汽车t小时行了300千米，平均每小时行( )千米。

6、李师傅每小时加工40个零件，a小时，一共加工了( )个。

7、每袋面粉重a千克，每袋大米重6千克，8袋面粉和5袋大米共重( )千克。

8、张刚每天上学时间为2小时，若他家到学校的路程为s千米，则他上学的速度为( )千米/时。

9、某实验中学初三年级12个班中共有团员a人，则初三年级平均每班团员数为( )人。

10、一张贺卡的价格为2元/个，教师节小明用自己积攒的零花钱买了c张贺卡送给老师，则小明一共花去( )元钱。

11、小明有m张卡片，比小强少3张，小强有卡片( )。

12、一个工地用汽车运土，每辆车运t吨。

上午运了6车，下午运了5车，这一天共运( )吨，上午比下午多运土( )吨。

13、一辆汽车t小时行了s千米，每小时行( )千米，行每千米要( )小时。

长方形的宽是a米，长是宽的1.8倍，面积是( )。

14、果园里有梨树a棵，苹果树的棵数比梨树的2倍多10棵。

果园里有苹果树（）棵，果园里苹果树与梨树共( )。

15、(1)作业本每本3.5元，c本作业本( )元。

(2)a+a+a+a+a用乘法表示为( )，3x用加法表示为( )。

(3)买一本故事书需要m元，买3本需要( )元，100元可以买( )本。

16、乘法分配率用字母表示是( )，加法结合律用字母表示( )。

二:求下列各式的值1、当a=18，b=2.5时，4a+2b=2、当x=0.5，y=1.3时，3v-4x=3、当a=2，b=10，x=2.4时，求下列各式的值。

用字母表示数量关系
人非圣贤，孰能无过？过而能改，善莫大焉。

《左传》
江缘学校陈思梅
一、请你填一填。

1．一只手有5个手指，两只手有10个手指，n只手有（）个手指。

2．四（1）班有学生a人，其中男生有27人，女生有（）人。

3．商店运进n盒彩笔，共计20元，每盒彩笔（）元。

4．明明比红红大2岁，今年红红a岁了，今年明明（）岁。

5．7×x 或 x ×7可以写成（）或（），也可以简写成（）。

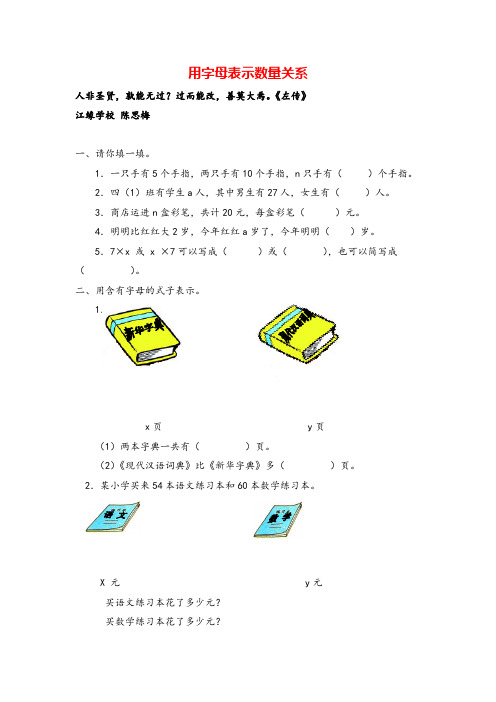
二、用含有字母的式子表示。

1．
x页 y页
（1）两本字典一共有（）页。

（2）《现代汉语词典》比《新华字典》多（）页。

2．某小学买来54本语文练习本和60本数学练习本。

X 元 y元
买语文练习本花了多少元？
买数学练习本花了多少元？
各买一本花多少元？
三、红红有a本课外书，亮亮比红红少7本，亮亮有（）本，他们俩一共
有（）本。

答案：
一、1. 5n 2. a-27 3. 20÷n 4.a+2 5. 7·x x·7 7x
二、1.(1) x+y (2)y-x 2. 54x 60y x+y
三、a-7 2a-7
【素材积累】
辛弃疾忧国忧民辛弃疾曾写《美芹十论》献给宋孝宗。

论文前三篇详细分析了北方人民对女真统治者的怨恨，以及女真统治集团内部的尖锐矛盾。

后七篇旧南宋方面应如何充实国力，积极准备，及时完成统一中国的事业等问题，提出了一些具体的规划。

但是当时宋金议和刚确定，朝廷没有采纳他的建议。

《用字母表示数量及数量关系》练习题一、课堂练习1、商店原来有120kg苹果，又运来了10箱苹果，每箱重 a kg。

（1）用式子表示出这个商店里苹果的总质量。

（2）根据这个式子，当a等于25时，商店一共有多少千克苹果？2、仓库里有货物96吨，运走了12车，每车运b吨。

（1）用式子表示仓库里剩下货物的吨数。

（2）根据这个式子，当b等于5时，仓库里剩下的货物有多少吨？（3）这里的b能表示哪些数？3、用字母式子表示下面的数量关系。

70加上a的和乘b。

x除以5的商加上n。

12的m倍，减去20的差。

42减去b的差除以5。

4、用字母式子表示下面的数（1）男生a人，女生b人。

全班平均每人捐7元，全班共捐款___ 元（2）苹果有120kg，卖出3箱，每箱y kg，现在还剩_____ kg苹果。

（3）一本书看了m天，每天看25页。

还剩k页没看，这本书共有____页5、拓展练习明明从家出发，每分钟行65米，a分可以到学校；东东从家出发，每分行75米，a分也可到学校。

从明明家到东东家一共有多少米？（先画一画位置关系再做题）二、课后练习1、填空（1）张刚每天上学时间为2小时，若他家到学校的路程为s千米，则他上学的速度为（）千米/时。

（2）某实验中学初三年级12个班中共有团员a人，则初三年级平均每班团员数为（）人。

（3）一张贺卡的价格为2元/个，教师节小明用自己积攒的零花钱买了c张贺卡送给老师，则小明一共花去（）元钱。

（4）一个长方形的长是 8m，宽是 am，则长方形的周长是（）cm。

（5）买一副羽毛球拍需要m元，买一副乒乓球板需要n元，则买6副羽毛球拍和8副乒乓球板共需要（）元。

（6）小李栽下1.8米高的小树苗，以后每年长0.3米，则t年后的树增高了（）米。

（7）妈妈今年a岁，明明今年b岁，10年后妈妈比明明大（）岁。

（8）小红把生日蛋糕平均分成n块，吃了7块，还剩（）块。

（9）小明每天攒a元钱，攒了10天，小明一共攒了（）元钱（10）王老师用χ分钟打了120 个字，平均每分钟打（）个字。

用字母表示数量关系
一、请你填一填。

1．一只手有5个手指，两只手有10个手指，n只手有（）个手指。

2．四（1）班有学生a人，其中男生有27人，女生有（）人。

3．商店运进n盒彩笔，共计20元，每盒彩笔（）元。

4．明明比红红大2岁，今年红红a岁了，今年明明（）岁。

5．7×x 或x ×7可以写成（）或（），也可以简写成（）。

二、用含有字母的式子表示。

1．
x页y页
（1）两本字典一共有（）页。

（2）《现代汉语词典》比《新华字典》多（）页。

2．某小学买来54本语文练习本和60本数学练习本。

X 元y元
买语文练习本花了多少元？
买数学练习本花了多少元？
各买一本花多少元？
三、红红有a本课外书，亮亮比红红少7本，亮亮有（）本，他们俩一共有（）
本。

答案：
一、1. 5n 2. a-27 3. 20÷n 4.a+2 5. 7·x x·7 7x
二、1.(1) x+y (2)y-x 2. 54x 60y x+y
三、a-7 2a-7。

课题—用字母表示复杂的数量关系知识点梳理知识点一：用字母表示运算定律和计算公式如果用字母a、b、c表示一个数，那么五个运算定律可以表示如下运算定律用字母表示简便记法加法交换律a+b=b+a 无加法结合律（a+b）+c=a+(b+c) 无乘法交换律a×b=b×a a .b=b .a或ab=ba乘法结合律(a×b)×c=a×(b×c) (a .b) .c=a .(b .c)或（ab）c=a(bc) 乘法分配律(a+b)×c=a×c + b×c (a+b) . c=a .c + b .c或（a+b）c=ac+bc 知识点二：用字母表示稍复杂的数量关系例1、：已知B是A的10倍，C是B的5倍，D是C的5倍.当A=1.5时，求 D+3C+3B+10A的值方法一：先分别求出B,C,D的值，再计算式子的值方法二：先把B,C,D都换成用A表示的式子，，最后把A的值代入式子计算用含有字母的式子表示题目中的数量关系时：1，先弄清题目中的数量关系是什么，再用含有字母的式子表示出来；2，可以利用乘法分配律，使式子更加简洁。

例2：公园里原来有20棵柳树，又栽了5行，每行x棵。

用含有字母的式子表示公园里现在柳树的棵数。

栽了5x棵，原有20棵，现在共有(20+5x)棵知识点三：方程的意义—等式的性质性质1、等式两边加上或减去同一个数，左右两边任然相等性质2、等式两边乘同一个数，或除以同一个不为0的数，左右两边任然相等方程必须满足的两个条件：1，含有未知数，2，是等式例：运用优化法解决天平秤物品问题要把一袋重210g的盐平均分成三份，可是手中的天平只配有一个5g和一个20g的砝码。

用这架天平至少要秤几次？思路导引：5g砝码+20g砝码=25g盐+25g砝码=50g盐+20g砝码=70g盐教学辅助练习1、我是公正的小法官。

（对的打“√”，错的打“×”）1. a+6可以写作6a。

人教版五年级上册数学用字母表示数及数量关系同步练习知识点1.用字母表示数和数量关系1.根据剪下的长方形透明胶的长度计算面积，并完成下表．练习1.填一填。

（1）我国青少年(7～17 岁)在1980 年平均身高xcm，到2000年，平均身高增长了6cm。

2000年我国青少年平均身高 cm。

（2）成年男子的标准体重通常用下面的式子表示：标准体重＝身高－105。

用含有字母的式子表示出成年男子的标准体重。

______________________2.我会填。

(1) 一种空调50台的总价是c元，那么一台空调的单价是( )元。

(2) 琪琪今年8岁，爸爸比他大a岁，爸爸今年( )岁。

(3) 一种糖果每千克a元，买20千克需( )元,买b千克需( )元。

(4) 婷婷家7月份的用水量是24.3吨，交水费a元，那么每吨水费( )元。

(5) 妈妈买xkg苹果，每千克苹果9.6元，妈妈买苹果花了( )元。

知识点2.用字母表示运算定律和计算公式1.在下面的里填上适当的数,用文字叙述以下运算定律。

25×＝79×12＋31＝31＋（1.2×25）×4＝1.2×（×）（32＋55）＋45＝32＋（＋）（6＋8）×＝×1.5＋×练习1.在中填上适当的字母或数。

x×＝2.6×＋b＝＋325×a＋b×＝（＋）×252.用简便方法计算下面各题，再用字母表示出来．知识点3：用字母表示计算公式1.把结果相等的两个式子连起来。

练习1．仔细想，认真填。

(1)一个等边三角形，边长为a m ，它的周长是( )m 。

(2)一个正方形的边长为a cm ，它的周长为( )cm ，它的面积为( )cm 2。

当a ＝5时，周长为()cm ，面积为( )cm 2。

2．判断。

(1) c ×3可以写成c 3。

( )(2) a 2一定大于2a 。

用字母表示数1.用字母表示定律和公式（1）用字母表示减法运算性质：a-b-c=______.（2）用字母表示除法运算性质：a÷b÷c＝______.（b≠0，c≠0）（3）用字母表示加法结合律是（a＋b）＋c＝______.（4）用字母表示乘法结合律是:(a×b)×c＝______.（5）图中阴影部分的面积是______.（6）在下图中，空白部分是个正方形。

用字母表示空白部分的面积是______，阴影部分的面积是______.（填编号）①a2；②b2；③（b-a）；④ab-a22.用字母表示数量关系（1）用含有字母的式子表示下面的数量关系。

a的3倍除40，商是______;m减去n的差的9倍是______.（2）用含有字母的式子表示下面的数量关系。

a的11倍加7，和是______;m与n的和除以8，商是______.（3）用含有字母的式子表示下面的数量关系。

m的5倍被7除，商是______;a与b的和的12倍是______.（4）用含有字母的式子表示：一堆黄沙共重y吨，运走2次后，还剩18吨，每次运走______吨.（5）用含有字母的式子表示：去年缴电费a元，今年比去年多缴55元，今年平均每月缴电费______元.（6）一辆车，上午开2小时，每小时行驶a千米，下午开2.5小时，每小时行驶b千米，这辆车总共行驶______千米.3.字母式的含义（1）林林今年x岁，妈妈今年35岁，两人的年龄之差是______岁.（填正确答案的序号）①x +35; ②x－35; ③35－x;（2）写出下面每个式子所表示的意义：学校买篮球，每个要a元，每个足球比篮球少5元，a－5表示____________（3）在校运动会上，四年级同学获得a枚金牌，五年级同学获得金牌数比四年级多7枚。

a+（a+7）表示______，当a=8时，四、五年级一共获得______枚金牌.（填编号）①四年级同学获得金牌数; ②四、五年级同学一共获得金牌数;③15枚; ④23枚.（4）王师傅有120米布，已经做了b套衣服，每套衣服用布2.5米，120－2.5b表示______,当b=16时，王师傅剩下的布有______米.（填编号）①b套衣服用布米数; ②剩下的米数; ③80; ④40;（5）正方形的边长为a分米，4a分米表示正方形的周长。