电路第十三章 拉普拉斯变换
- 格式:pdf
- 大小:356.85 KB
- 文档页数:39





电路第十三章拉普拉斯变换第十三章拉普拉斯变换内容提要本章介绍拉普拉斯变换法在线性电路分析中的应用。
主要内容有:拉普拉斯变换的定义,拉普拉斯变换与电路分析有关的一些基本性质,求拉普拉斯反变换的部分分式法(分解定理),还将介绍KCL和KVL的运算形式,运算阻抗,运算导纳及运算电路,并通过实例说明它们在电路分析中的应用。
目录§13—1拉普拉斯变换的定义§13—2拉普拉斯变换的基本性质§13—3拉普拉斯反变换的部分分式展开§13—4运算电路§13—5应用拉普拉斯变换法分析线性电路本章作业13—1(2)(4)(6)(8)、13—2(1)(3)、13—3(2)(4)、13—4、13—12、12—16、12—18§13—1拉普拉斯变换的定义拉普拉斯变换是一种数学变换。
定义:F()=∫f(t)e–tdt0–∞S=σ+jω拉普拉斯正变换1σ+j∞F()etdf(t)=拉普拉斯反变换2πj∫σ–j∞拉氏正变换f(t)拉氏反变换F()=L[f(t)]原函数一一对应象函数f(t)=L–1[F()]F()简写符号例:计算下列原函数的象函数;1.f(t)=ε(t)2.f(t)=δ(t)∞0–3.f(t)=e–αtε(t)4.f(t)=tε(t)解:F()=∫f(t)e–tdt1.F()=L[ε(t)]=∫∞0–ε(t)e–tdt=∫0∞–e–tdt=0+1–t–e1=0–∞∞2.F()=L[δ(t)]=∫δ(t)e–tdt=∫δ(t)dt=10–0–∞3.F()=L[e–αtε(t)]=∫∞∞0–e–αte–tdt=1e–(α+)t–α+∞0–1=α+0–124.F()=L[tε(t)]=∫=–1[te–t0–同理:F()=L[tnε(t)]=n!n+1te–tdt–∫∞0–e–tdt]=§13—2拉普拉斯变换的基本性质一、线性性质若:L[f1(t)]=F1()L[f2(t)]=F2()则:L[A1f1(t)+A2f2(t)]=A1F1()+A2F2()证:L[A1f1(t)+A2f2(t)]=∫[A1f1(t)+A2f2(t)]e–tdt0–∞=∫A1f1(t)e–tdt+∫0A2f2(t)e–tdt0––∞∞=A1∫0f1(t)e–tdt+A2∫f2(t)e–tdt–∞∞0–=A1F1()+A2F2()例:计算下列原函数的象函数;1、常数U解:1、L[U]=L[Uε(t)]=U2、L[A(1–e–αt)]=L[A]–L[Ae–αt]=3、L[inωt]=L[1ejωt–2j11–=2j–jωαAA–A+α=(+α)2、A(1–e–αt)3、inωt1–jωte]2jω112j+jω=2+ω2同理:L[coωt]=22+ω二、(时域)微分性质设:L[f(t)]=F()则:L[f′(t)]=F()–f(0–)证:L[f′(t)]=∫∞df(t)0–dte–tdt=∫e–tdf(t)0–∞=e–tf(t)∞0––∫f(t)(–)e–tdt∞0–0–∞=–f(0–)+∫f(t)e–tdt=F()–f(0–)导数性质的意义在于把原函数求导数的运算转换为象函数乘以再减去初始值的代数运算。

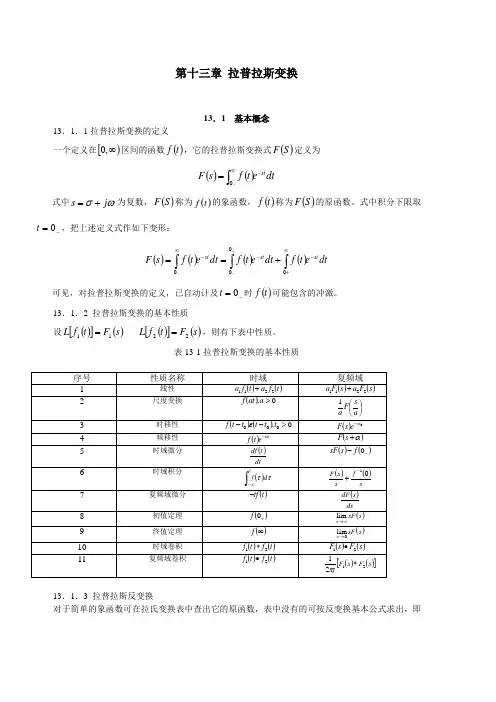
第十三章 拉普拉斯变换13.1 基本概念13.1.1拉普拉斯变换的定义一个定义在[)∞,0区间的函数()t f ,它的拉普拉斯变换式()S F 定义为()()dt e t f s F st -∞⎰-=0式中ωσj s +=为复数,()S F 称为()t f 的象函数,()t f 称为()S F 的原函数。
式中积分下限取-=0t ,把上述定义式作如下变形:()()()()dt e t f dt e t f dt e t f s F st stst-∞+--∞⎰⎰⎰+==+--0000可见,对拉普拉斯变换的定义,已自动计及-=0t 时()t f 可能包含的冲激。
13.1.2 拉普拉斯变换的基本性质设()[]()s F t f L 11= ()[]()s F t f L 22=,则有下表中性质。
表13-1拉普拉斯变换的基本性质13.1.3 拉普拉斯反变换对于简单的象函数可在拉氏变换表中查出它的原函数,表中没有的可按反变换基本公式求出,即()()[]()ds e s F js F L t f stj c j c ⎰∞+∞--==π211,但此式涉及到计算一个复变函数的积分,一般比较复杂。
电路响应的象函数通常可表示为两个实系数的s 的多项式之比,即s 的一个有理分式()()()nn n mm m b s b s b a s a s a s D s N s F ++++++==-- 110110 式中m 和n 为正整数,且m n ≥。
若m n =时,先将其化简成真分式,然后用部分分式展开,将复杂变换式分解为许多简单变换式之和,然后分别查表即可求得原函数。
1.()0=s D 具有n 个单实根时()iini p s K s F -=∑=1式中:()()i p s i i s F p s K =-=|则 ()()[]t p ni i ie K s F Lt f ∑=-==112.()0=s D 具有重根时设()0=s D 除了m 个重根外,其它均为单根,共有n 个根。



第十三章拉普拉斯变换经典法——依照电路列出微分方程然后进行求解来求解动...(求解时刻函数方程)。
态电路响应的方式。
也叫时域解法....优势:物理概念清楚,便于明白得。
可是这种方式关于求解二阶以上的复杂电路,很困难。
即便是一阶电路,当鼓励为常数、正弦函数与冲击函数时,应用三要素法进行时域分析是方便的,但当鼓励为指数函数、斜坡函数、专门是任意函数式,时域分析也是很麻烦的。
在正弦稳态分析中,采纳向量法后,将时域中的微积分运算转化成了频域中的代数运算,使运算十分简单。
向量分析是一种变换。
在暂态分析中,可否也成立这种类似的变换?拉普拉斯变换(简称拉氏变换)线性定常电路的拉氏变换分析与向量分析十分相似,用拉氏变换求解动态电路,先将时域函数通过拉氏变换变成复频域(S域)函数,并画出S域电路,在S域电路中确信响应后,通过拉氏反变换取得时域响应。
这种分析法不用求特解、通解、及确信积分常数,所得结果确实是全响应。
拉氏变换将时域中的微积分方程变成S域中的代数方程。
因为拉氏变换分析要通过求拉氏变换和反变换两次运算(变换),因此也称为运算法...。
运算法是一种通过数学变换间接求解动态电路的简捷方式。
应当指出,拉氏变换求解动态电路,只适用于线性,非时变的电路,不适用于时变及非线性电路。
§15-1 拉普拉斯变换的概念一、 拉氏变换的概念先概念一个复数 ωδj s +=其中δ是使函数)(t f 在区间(0-,∞)内积分收敛而选定的一个常数;ω是角频率,是变量;s 是复变量。
δ、ω、s 的单位都是1/秒。
复变量s 也称为广义频率,或复频率。
1、 拉氏正变换的概念概念在(0-,∞)内的时刻函数)(t f ()(t f 代表电路中的鼓励,或响应),与因子ste -相乘,组成一个新的函数st e t f -)(,再在(0-,∞)内对t 积分,该积分称为单边拉普拉斯(Laplace )正变换,简称拉氏变换。
⎰∞--== 0 )()()]([dt e t f s F t f L st式中 ωδj s +=为复数(复频率变量)上式对t 求定积分后,变成了复变量s 的函数,因此记作)(s F 。