下载文档原格式
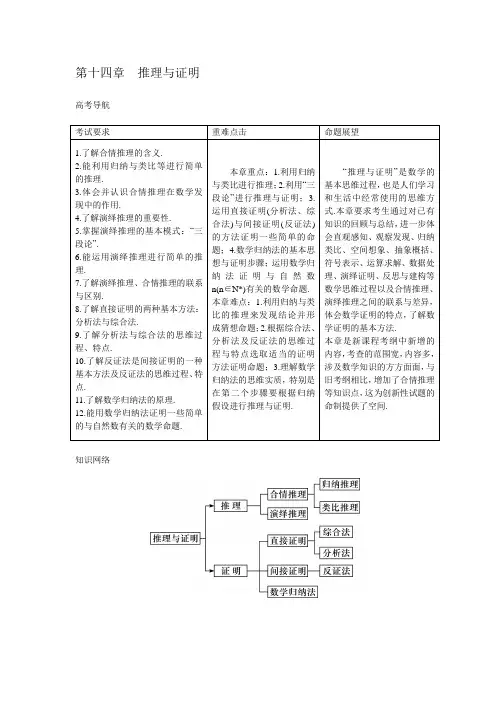
第十四章推理与证明高考导航知识网络14.1 合情推理与演绎推理典例精析题型一 运用归纳推理发现一般性结论【例1】 通过观察下列等式，猜想出一个一般性的结论，并证明结论的真假. sin215°＋sin275°＋sin2135°＝32；sin230°＋sin290°＋sin2150°＝32；sin245°＋sin2105°＋sin2165°＝32；sin260°＋sin2120°＋sin2180°＝32.【解析】猜想：sin2(α－60°)＋sin2α＋sin2(α＋60°)＝32.左边＝(sin αcos 60°－cos αsin 60°)2＋sin2α＋(sin αcos 60°＋cos αsin 60°)2＝32(sin2α＋cos2α)＝32＝右边. 【点拨】先猜后证是一种常见题型；归纳推理的一些常见形式：一是“具有共同特征型”，二是“递推型”，三是“循环型”(周期性).【变式训练1】设直角三角形的两直角边的长分别为a ，b ，斜边长为c ，斜边上的高为h ，则有a ＋b ＜c ＋h 成立，某同学通过类比得到如下四个结论：①a2＋b2＞c2＋h2；②a3＋b3＜c3＋h3；③a4＋b4＜c4＋h4；④a5＋b5＞c5＋h5. 其中正确结论的序号是 ；进一步类比得到的一般结论是 . 【解析】②③；an ＋bn ＜cn ＋hn(n ∈N*). 题型二 运用类比推理拓展新知识 【例2】 请用类比推理完成下表：【解析】 本题由已知的前两组类比可得到如下信息： ①平面中的三角形与空间中的三棱锥是类比对象；②三角形各边的边长与三棱锥各面的面积是类比对象；③三角形边上的高与三棱锥面上的高是类比对象；④三角形的面积与三棱锥的体积是类比对象；⑤三角形的面积公式中的“二分之一”与三棱锥的体积公式中的“三分之一”是类比对象.由以上分析可知：故第三行空格应填：三棱锥的体积等于其内切球半径与三棱锥表面积的乘积的三分之一. 本题结论可以用等体积法，将三棱锥分割成四个小的三棱锥去证明，此处从略.【点拨】类比推理的关键是找到合适的类比对象.平面几何中的一些定理、公式、结论等，可以类比到立体几何中，得到类似的结论.一般平面中的一些元素与空间中的一些元素的类比列表如下：【变式训练2】面积为S 的平面凸四边形的第i 条边的边长记为ai(i ＝1,2,3,4)，此四边形内任一点P 到第i 条边的距离为hi(i ＝1,2,3,4)，(1)若a11＝a22＝a33＝a44＝k ，则∑=41i iih＝ ；(2)类比以上性质，体积为V 的三棱锥的第i 个面的面积记为Si(i ＝1,2,3,4)，此三棱锥内任一点Q 到第i 个面的距离记为Hi(i ＝1,2,3,4)，若S11＝S22＝S33＝S44＝K ，则∑=41i iiH＝ .【解析】2S k ；3VK.题型三 运用“三段论”进行演绎推理 【例3】已知函数f(x)＝ln ax －x －ax (a ≠0).(1)求此函数的单调区间及最值；(2)求证：对于任意正整数n ，均有1＋12＋13＋…＋1n ≥ln enn ！.【解析】(1)由题意f ′(x)＝x －ax2. 当a ＞0时，函数f(x)的定义域为(0，＋∞)，此时函数在(0，a)上是减函数，在(a ，＋∞)上是增函数， fmin(x)＝f(a)＝ln a2，无最大值.当a ＜0时，函数f(x)的定义域为(－∞，0)，此时函数在(－∞，a)上是减函数，在(a,0)上是增函数， fmin(x)＝f(a)＝ln a2，无最大值.(2)取a ＝1，由(1)知，f(x)＝ln x －x －1x≥f(1)＝0，故1x ≥1－ln x ＝ln e x， 取x ＝1,2,3，…，n ，则1＋12＋13＋…＋1n ≥ln e ＋ln e 2＋…＋ln e n ＝ln en n ！.【点拨】演绎推理是推理证明的主要途径，而“三段论”是演绎推理的一种重要的推理形式，在高考中以证明题出现的频率较大.【变式训练3】已知函数f(x)＝eg(x)，g(x)＝kx －1x ＋1(e 是自然对数的底数)，(1)若对任意的x ＞0，都有f(x)＜x ＋1，求满足条件的最大整数k 的值； (2)求证：ln(1＋1×2)＋ln(1＋2×3)＋…＋ln[1＋n(n ＋1)]＞2n －3(n ∈N*). 【解析】(1)由条件得到f(1)＜2⇒11-2e +x x ＜2⇒k ＜2ln 2＋1＜3，猜测最大整数k ＝2，现在证明11-2e +x x ＜x ＋1对任意x ＞0恒成立：11-2e +x x ＜x ＋1等价于2－3x ＋1＜ln(x ＋1)⇔ln(x ＋1)＋3x ＋1＞2， 设h(x)＝ln(x ＋1)＋3x ＋1，则h ′(x)＝1x ＋1－3(x ＋1)2＝x －2(x ＋1)2.故x ∈(0,2)时，h ′(x)＜0，当x ∈(2，＋∞)时，h ′(x)＞0. 所以对任意的x ＞0都有h(x)≥h(2)＝ln 3＋1＞2，即11-2e +x x ＜x ＋1对任意x ＞0恒成立，所以整数k 的最大值为2.(2)由(1)得到不等式2－3x ＋1＜ln(x ＋1)，所以ln[1＋k(k ＋1)]＞2－3k(k ＋1)＋1＞2－3k(k ＋1)，ln(1＋1×2)＋ln(1＋2×3)＋…＋ln[1＋n(n ＋1)]＞(2－31×2)＋(2－32×3)＋…＋[2－3n(n ＋1)]＝2n －3[11×2＋12×3＋…＋1n(n ＋1)]＝2n －3＋3n ＋1＞2n －3，所以原不等式成立. 总结提高合情推理与演绎推理是两种基本的思维推理方式.尽管合情推理(归纳、类比)得到的结论未必正确，但归纳推理与类比推理具有猜想和发现新结论、探索和提供证明的新思路的重要作用，特别在数学学习中，我们可以由熟悉的、已知的知识领域运用归纳、类比思维获取发现和创造的灵感去探索陌生的、未知的知识领域.演绎推理是数学逻辑思维的主要形式，担负着判断命题真假的重要使命.如果说合情推理是以感性思维为主，只需有感而发；那么演绎推理则是以理性思维为主，要求言必有据.在近几年高考中一道合情推理的试题往往会成为一套高考试题的特色与亮点，以彰显数学思维的魅力.其中数列的通项公式、求和公式的归纳、等差数列与等比数列、平面与空间、圆锥曲线与圆、杨辉三角等的类比的考查频率较大.而演绎推理的考查则可以渗透到每一道试题中.。
