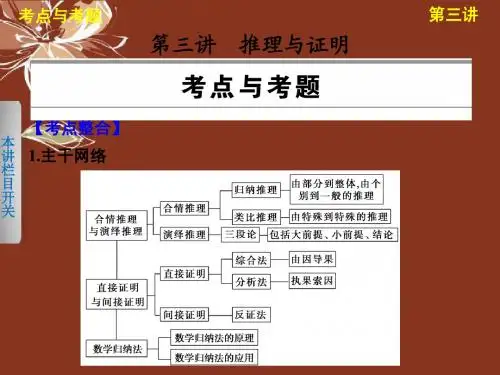
推理与证明PPT优秀课件
- 格式:ppt
- 大小:4.89 MB
- 文档页数:18

函数的证明与推理课件函数的证明与推理在数学领域中,函数的证明与推理是一项重要的技能。
通过证明和推理,我们可以得到对函数性质的深刻理解,并在解决数学问题时做出精确的推断和推理。
本课件将介绍函数的证明与推理的基本概念和方法,帮助读者提升这一方面的技能。
一、函数的定义与特性在开始论述函数的证明与推理之前,我们先来回顾一下函数的基本定义和特性。
函数是一个自变量和因变量之间的映射关系,通常表示为f(x),其中x为自变量,f(x)为因变量。
函数有着以下几个重要特性:1. 函数的定义域与值域:定义域是指自变量的集合,值域是指函数取值的集合。
在证明和推理中,我们需要确定函数的定义域和值域,确保推导的严谨性。
2. 函数的奇偶性:当函数满足f(-x) = f(x)时,我们称其为偶函数;当函数满足f(-x) = -f(x)时,我们称其为奇函数。
在证明中,奇偶性的性质可用于简化推理过程。
3. 函数的单调性:函数的单调性分为递增和递减两种。
当函数满足f(x1) ≤ f(x2)时,称其为递增函数;当函数满足f(x1) ≥ f(x2)时,称其为递减函数。
单调性在证明中常常用于确定函数的极值点和临界点。
二、函数的证明方法1. 直接证明法:直接证明法是一种常用的证明方法,通过列出已知条件和证明结论,逐步演绎证明的正确性。
在函数的证明中,我们需要清晰地列出假设条件、使用数学定理和性质,并逐步推导出目标结论。
2. 反证法:反证法是一种常用的证明方法,通过假设结论不成立,推导出矛盾的结果,从而证明原始结论的正确性。
在函数的证明中,我们可以运用反证法来证明函数的特定性质,如存在唯一性等。
3. 数学归纳法:数学归纳法是一种常用的证明方法,用于证明满足自然数集上的性质。
在函数的证明中,数学归纳法可以用于证明递推关系、等式等。
三、函数的推理方法1. 等式推理:等式推理是函数推理中最基本的方法,通过运用等式的性质,将一个等式变换为另一个等式,以推导出目标结果。