下载文档原格式
范数等价判别定理的证明范数等价判别定理是泛函分析中的一个重要结果，它表明在有限维赋范空间中的所有范数是等价的。
以下给出范数等价判别定理的证明。
首先，设$X$是一个有限维赋范空间，记$n = \dim(X)$。
证明思路：我们需要证明任意两个范数$\|\cdot\|_a$和$\|\cdot\|_b$等价，即存在常数$c_1>0$和$c_2>0$使得对于任意的向量$x\in X$，有$c_1\|x\|_a \leq \|x\|_b \leq c_2\|x\|_a$。
首先证明$\|\cdot\|_a$和$\|\cdot\|_b$等价的充分性，即存在$c_2>0$使得对于任意的向量$x\in X$，有$\|x\|_b \leqc_2\|x\|_a$。
由于$X$是有限维空间，我们可以选取$X$的一组基$\{e_1,e_2,\ldots,e_n\}$。
对于任意的向量$x\in X$，我们可以将其表示为$x = \sum_{i=1}^n x_ie_i$。
其中$x_i$是标量。
我们要证明存在常数$c_2>0$使得$\|x\|_b \leq c_2\|x\|_a$成立。
由范数的定义可知，$\|x\|_a = \left(\sum_{i=1}^n|x_i|^a\right)^{\frac{1}{a}}$，$\|x\|_b = \left(\sum_{i=1}^n|x_i|^b\right)^{\frac{1}{b}}$。
考虑$\frac{1}{a}$和$\frac{1}{b}$之间的大小关系：若$\frac{1}{a} > \frac{1}{b}$，则对于任意的$i=1,2,\ldots,n$，有$|x_i|^a \geq |x_i|^b$，进而$\left(\sum_{i=1}^n|x_i|^a\right)^{\frac{1}{a}} \geq \left(\sum_{i=1}^n|x_i|^b\right)^{\frac{1}{b}}$。
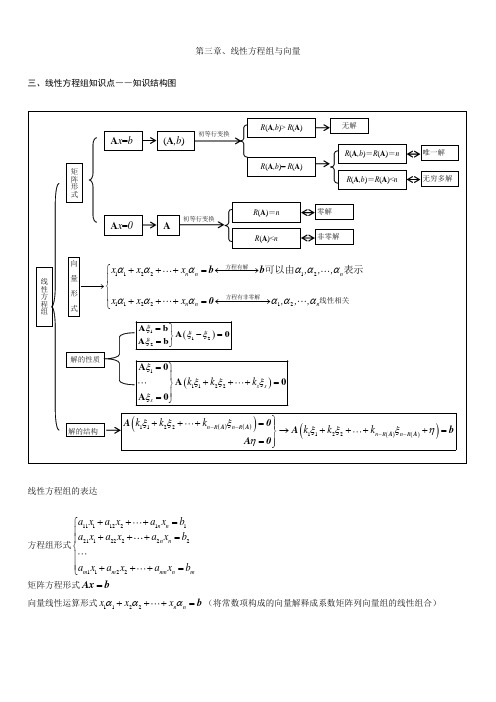
第三章、线性方程组与向量三、线性方程组知识点――知识结构图线性方程组的表达方程组形式11112211211222221122n n n n m m mn n ma x a x a xb a x a x a x b a x a x a x b +++=⎧⎪+++=⎪⎨⎪⎪+++=⎩矩阵方程形式=Ax b向量线性运算形式1122n n x x x ααα+++=b （将常数项构成的向量解释成系数矩阵列向量组的线性组合）()12-=⎬⎭ξξA 0b ()11122s s k k k =⎫⎪+++=⎬⎪=ξξξξξA 0A 0A 0()())(1122n R n R k k k k ξξξξ--⎫+++=⎪→⎬A A 0A向量组、线性方程组、矩阵的关系图求解齐次线性方程组如何确定自由变量并赋值？○1对系数矩阵实施初等行变换，将其化为最简形矩阵； ○2每个非零行的非零首元对应的未知量确定为非自由未知量（()R r =A 个非自由未知量），剩下的()n R -A 未知量确定为自由未知量；○3每次给一个自由未知量赋值为1，其余的自由未知量赋值为0（共需赋值()n R -A 次）。
（见P110例1） 向量组的等价（扩展知识）向量组的等价是指：它们可以相互线性表示，它们所含有的向量个数可以不一样。
理解的关键还是认识到向量由向量组线性表示，以及如何表达（P 94 定义6）。
①含有相同个数向量的向量组的等价问题 （例：习题3.3的8、9题），关于向量组12s :,,,αααA ，向量组12s :,,,βββB 的等价，()()1212n s n s s s s s ,,,,,,βββααα⨯⨯⨯⇔=B =A K K（以P 95 习题3.3的8题为例）给出了向量的分量值，即给出了向量组对应的矩阵元素，那么424222⨯⨯⨯B =A K 与424222⨯⨯⨯=A B R 同时成立，则两个向量组等价；于是问题变换为矩阵方程()()111212122122x x ,,x x ββαα⎛⎫⎪⎝⎭=有解存在（其中()()1212,,,ββαα均不是方阵）。
第三章 线性方程组的解法一、基本内容提要1. 高斯消元法高斯消去法（Gauss Elimination Method ）是一种规则化的加减消元法。
基本思想是通过逐次消元计算把需要求解的线性方程组转化为上三角形方程组，即把线性方程组的系数矩阵转化为上三角矩阵，从而使一般线性方程组的求解转化为等价(同解)的上三角形方程组的求解。
2. 高斯消元法的消元过程求解n 元线性方程组的Gauss 消元法的一般步骤，将方程组设为如下形式⎪⎪⎩⎪⎪⎨⎧=+++=+++=+++)1()1(2)1(21)1(1)1(2)1(22)1(221)1(21)1(1)1(12)1(121)1(11 nn nn n n n n n n b x a x a x a b x a x a x a b x a x a x a 可简记为)1()1(b x A=，其中b b A A ==)1()1(,。
第一步：设,0)1(11≠a 记),3,2(/)1(11)1(11n i a a l i i ==，将上式中第i 个方程减去第1个方程乘以),3,2(1n i l i =，完成第一次消元，得其同解方程组⎪⎪⎩⎪⎪⎨⎧=++=++=+++)2()2(2)2(2)2(2)2(22)2(22)1(1)1(12)1(121)1(11n n nn n n n n n b x a x a b x a x a b x a x a x a 其中),,3,2,(,)1(11)1()2()1(11)1()2(n j i b l b b a l a a i i ij i ij ij =-=-=。
此方程组简记为)2()2(b x A =。
第二步：设,0)2(22≠a ，记),,3(/)2(22)2(22n i a a l i i ==。
将上式中第i 个方程减去第2个方程乘以),,3,2(2n i l i =，完成第二次消元。
第1-k 步：设1-k 次消元完成后得原方程组的同解方程组为)()()()()()()1(2)2(2)2(22)2(22)1(1)1(1)1(12)1(121)1(11⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧=++=++=++++=+++++k n n k nn k k nk k kn k kn k k kk n n k k n n k k b x a x a b x a x a b x a x a x a b x a x a x a x a 简记为)()(k k b x A=。
