32频数分布直方图同步练习

北师大版七年级数学上册《6.3.2频数直方图》同步测试题带答案学校:___________班级：___________姓名：___________考号：___________【基础达标】1.在一次数学测试中,将某班40名学生的成绩分为5组,第一组到第四组的频率之和为0.8,则第5组的频数是()A.7B.8C.9D.102.一个容量为80的样本,最大值是141,最小值是50,取组距为10,可以分成()A.10组B.9组C.8组D.7组3.小明统计了他家今年5月份打电话的次数及通话时间,并列出了频数分布表:通话时间x/min0<x≤55<x≤1010<x≤1515<x≤20频数(通话次数)201695通话时间不超过15 min的频率为()A.0.1B.0.18C.0.5D.0.94.如图,这是某单位职工年龄的频数分布直方图,根据图形提供的信息,回答下列问题:(1)组距为多少?组数呢?(2)该单位共有多少名职工?不小于38岁且小于44岁的职工有多少?占职工总人数的百分之几?(3)如果42岁的职工有4人,那么42岁以上的职工有多少人?【能力巩固】5.某班级的一次数学考试成绩统计图如图所示,则下列说法正确的是()A.该班的总人数为41B.得分在60~70分的人数最多C.人数最少的得分段的频数为2D.得分及格(≥60分)的有35人6.对150个数据进行整理得到频数分布直方图,测得所有表示频数的长方形的高之和为33 cm,其中最高的长方形的高度为11 cm,则这个最高的长方形的高所表示的频数为人.7.七(3)班40名学生的某次数学测验成绩如下:63,84,91,53,69,81,61,69,91,78,75,81,80,67,76,81,79,94,61,69,89,70,70,87,81,86,90,8 8,85,67,71,82,87,75,87,95,53,65,74,77.(1)请你按10分的组距分段,画出频数分布直方图.(2)请你统计一下这次数学测验的及格率(60分以上含60分为及格)及优秀率(90分以上含90分为优秀).(3)请说明哪个分数段的学生最多?哪个分数段的学生最少?【素养拓展】8.为了解冬训效果,某足球运动基地对参训队员进行一次体质检测.已知本次检测满分为100分,测试成绩取整数,测试结束后将测试成绩制成尚不完整的频数分布表和频数分布直方图.从测试结果来看,每名队员的成绩均超过50分.分组频数频率50.5~60.540.0860.5~70.5a c70.5~80.5160.3280.5~90.5b90.5~100.5160.32合计 1.00请解答下列问题:(1)a=,b=,c=.(2)补全频数分布直方图.(3)若成绩在70分以上为冬训效果显著,同时冬训效果显著的人数占总人数的70%以上,就表示该基地冬训方案科学,请根据上述数据分析该基地冬训方案是否科学,并说明理由.参考答案【基础达标】1.B2.A3.D4.解:(1)2;7.(2)50人;30人;60%.(3)15人.【能力巩固】5.C6.507.解:(1)第一步,分组及统计每组数据的频数(每组含前一个边界值,不含后一个边界值)成绩x/分频数50~60 260~70 970~80 1080~90 1490~100 5第二步,绘制频数分布直方图如下:(2)及格率为95%,优秀率为12.5%.(3)从图中可以清楚地看出80到90这个分数段的学生数最多,50分到60分这个分数段的学生数最少.【素养拓展】8.解:(1)8;6;0.16.(2)补全的频数分布直方图如下:(3)该基地冬训方案科学.理由:由题意知70分以上的人数为16+6+16=38(人).因为×100%=76%>70%冬训效果显著的人数占总人数的百分比为3850所以该基地冬训方案科学.。

3.2 频数分布直方图【知识盘点】1.用来表示________________的基本统计图叫做频数分布直方图，•简称___________．2．在对样本数据进行分组统计时，若第一组的组别为67.5～72.5，则这一组的组中值是_________．3．已知一个样本的样本容量为50，在频数分布直方图中，各小长方形的高比为2：3：4：1，那么第二组的频数是__________．4．当数据个数为奇数时，可用频数分布直方图中的某一组的______•作为中位数的估计值；当数据个数为偶数时，可用频数分布直方图中某两组的_______作为中位数的估计值．【基础过关】5．在绘制频数分布直方图时，各个小长方形的高等于相应各组的（）A．频数 B．组距 C．组中值 D．频率6．某个样本的频数分布直方图中一共有4组，从左至右的组中值依次为5，8，•11，14，频数依次为5，4，6，5，则频率为0.2的一组为（）A．6.5～9.5 B．9.5～12.5 C．8～11 D．5～87．八（1）班若干名学生每分跳绳次数的频数分布直方图如图1所示，由直方图可知，这若干名学生平均每分钟跳绳的次数（结果精确到个位）约为（）A．87 B．100 C．104 D．112(1) (2)8．某篮球队队员年龄结构直方图如图2所示，根据图中信息，可知该队队员年龄的中位数为（）A．18岁B．21岁 C．23岁 D．19．5岁【应用拓展】9．要了解某地区八年级学生的身高情况，从中随机抽取150名学生的身高作为一个样本，身高均在141～175cm之间（取整数厘米），整理后分成7组，绘制出频数分布直方图（不完整），根据图中提供的信息，解答下列问题：（1）补全频数分布直方图；（2）抽取的样本中，学生身高的中位数在哪个小组？（3）该地区共有3000名八年级学生，估计其中身高不低于161cm的人数．【综合提高】10．某年级组织学生参加夏令营，分为甲、乙、丙三组进行活动．•下面两幅统计图反映了学生报名参加夏令营的情况．请你根据图中的信息回答下列问题：报名人数分布直方图报名人数扇形统计图（1）求该年级报名参加本次活动的总人数；（2）求该年级报名参加乙组的人数，并补全频数分布直方图；（3）根据实际情况，需从甲组抽调部分同学到丙组，使丙组人数是甲组人数的3倍，那么，应从甲组抽调多少名学生到丙组？参考答案1．频数分布，直方图 2．70 3．20 4．组中值，交界值5．A 6．A 7．C 8．B •9．（1）第三组的频数为27，图略（2）中位数落在155.5～160.5内（3）960人10．（1）50人（2）10人，图略（3）设抽调x名，则25+x=3（15-x），解得x=5，即5名。

频率分布直方图小练1.为增强市民的环保意识，某市面向全市增招环保知识义务宣传志愿者.从符合条件的志愿者中随机选取名志愿者,其年龄频率分布直方图如图所示,其中年龄(岁)分成五组:第组,第组,第组,第组,第组.得到的频率分布直方图(局部)如图所示.（1）求第组的频率,并在图中补画直方图；（2）从名志愿者中再选出年龄低于岁的志愿者名担任主要宣讲人,求这名主要宣讲人的年龄在同一组的概率.解析（1）0.3，图见：（1）第4组的频率为.....1分, ............................2分,则补画第4组的直方图如图所示：.............................................4分（２）设“从20名志愿者中再选出年龄低于30岁的志愿者3名担任主要宣讲人, 其年龄均在同一组”为事件A...............................................5分第一组的人数为人第二组的人数为人......................6分设第一组的志愿者为m，第二组的4名志愿者分别为a,b,c,d.......................7分从m, a,b,c,d中选出3名志愿者共有10种选取方法。

.........10分其中都在第二组的共有4种选取方法..........11分所以，所求事件的概率为........................12分2.某校为了解高一期末数学考试的情况，从高一的所有学生数学试卷中随机抽取份，试卷进行成绩分析，得到数学成绩频率分布直方图（如图所示），其中成绩在的学生人数为6.（Ⅰ）估计所抽取的数学成绩的众数；（Ⅱ）用分层抽样的方法在成绩为和这两组中共抽取5个学生，并从这5个学生中任取2人进行点评，求分数在恰有1人的概率.考点6.统计图表解析解：（Ⅰ）由频率分布直方图可知：样本的众数为75．…………3分（Ⅱ）由频率分布直方图可得：第三组的频率：，所以，…………………………………………4分第四组的频数：；第五组的频数：；用分层抽样的方法抽取5份得：第四组抽取：；第五组抽取：．……7分记抽到第四组的三位同学为，抽到第五组的两位同学为则从5个同学中任取2人的基本事件有：，，共10种．其中分数在恰有1人有：，共6种．所求概率：．……………………………12分3.某校研究性学习小组从汽车市场上随机抽取20辆纯电动汽车调查其续驶里程（单次充电后能行驶的最大里程），被调查汽车的续驶里程全部介于公里和公里之间，将统计结果分成组：，，，，，绘制成如图所示的频率分布直方图．（Ⅰ）求直方图中的值；（Ⅱ）求续驶里程在的车辆数；（Ⅲ）若从续驶里程在的车辆中随机抽取2辆车，求其中恰有一辆车的续驶里程为的概率.考点6.统计图表解析解:（Ⅰ）由直方图可得：∴.------------------3分（Ⅱ）由题意可知，续驶里程在的车辆数为：------------------5分（Ⅲ）由（Ⅱ）及题意可知，续驶里程在的车辆数为，分别记为，续驶里程在的车辆数为，分别记为，设事件“其中恰有一辆汽车的续驶里程为”----------------------7分从该辆汽车中随机抽取辆，所有的可能如下：共种情况，----------------10分事件包含的可能有共种情况，则.------------------12分4.某中学高三(1)班共有50名学生，他们每天自主学习的时间在180到330分钟之间，将全班学生的自主学习时间作分组统计，得其频率分布如下表所示：组序分组频数频率第一组[180，210)50.1第二组[210，240)100.2第三组[240，270)120.24第四组[270，300)a b第五组[300，330)6c(1)求表中a、b、c的值；(2)某课题小组为了研究自主学习时间与成绩的相关性，需用分层抽样的方法从这50名学生中随机抽取20名作统计分析，则在第二组学生中应抽取多少人？(3)已知第一组学生中有3名男生和2名女生，从这5名学生中随机抽取2人，求恰好抽到1名男生和1名女生的概率．某单位N名员工参加“社区低碳你我他”活动，他们的年龄在25岁至50岁之间。

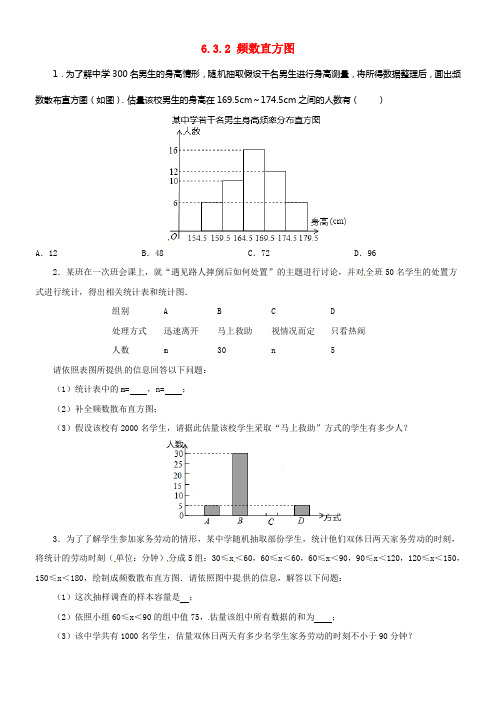
6.3.2 频数直方图1．为了解中学300名男生的身高情形，随机抽取假设干名男生进行身高测量，将所得数据整理后，画出频数散布直方图（如图）．估量该校男生的身高在169.5cm～174.5cm之间的人数有（）A．12 B．48 C．72 D．96 2．某班在一次班会课上，就“遇见路人摔倒后如何处置”的主题进行讨论，并对全班50名学生的处置方式进行统计，得出相关统计表和统计图．组别 A B C D处理方式迅速离开马上救助视情况而定只看热闹人数m 30 n 5请依照表图所提供的信息回答以下问题：（1）统计表中的m= ，n= ；（2）补全频数散布直方图；（3）假设该校有2000名学生，请据此估量该校学生采取“马上救助”方式的学生有多少人？3．为了了解学生参加家务劳动的情形，某中学随机抽取部份学生，统计他们双休日两天家务劳动的时刻，将统计的劳动时刻（单位：分钟）分成5组：30≤x＜60，60≤x＜60，60≤x＜90，90≤x＜120，120≤x＜150，150≤x＜180，绘制成频数散布直方图．请依照图中提供的信息，解答以下问题：（1）这次抽样调查的样本容量是；（2）依照小组60≤x＜90的组中值75，估量该组中所有数据的和为；（3）该中学共有1000名学生，估量双休日两天有多少名学生家务劳动的时刻不小于90分钟？参考答案1．C2．解：（1）依照条形图能够取得：m=5，n=50﹣5﹣30﹣5=10（人）故答案是：5，10；（2）；（3）2000×=1200（人）．3. 解：（1）这次抽样调查的样本容量是：5+20+35+30+10=100；（2）因为小组60≤x＜90的组中值75，因此该组中所有数据的和为：75×20=1500；（3）依照题意得：1000×=750（人）．答：该中学双休日两天有750名学生家务劳动的时刻不小于90分钟．故答案为：100，1500．。

频率分布直方图北鲲五班练习题1.用样本估计总体，下列说法正确的是（）A．样本的结果就是总体的结果B．样本容量越大，估计就越精确C．样本的标准差可以近似地反映总体的平均状态D．数据的方差越大，说明数据越稳定2．一支田径队有男队员56人，女队员42人，用分层抽样的方法从全体运动员中抽出一个容量为28的样本，则应抽取男队员的人数为（）A．12 B．14 C．16 D．183.某学校有教职工共160人，其中有教师104人，管理人员32人，后勤服务人员24人，要从中抽取一个容量为20的样本，用分层抽样的方法抽取样本，则在20人的样本中应抽取后勤人员的人数为( )A. 3B. 4C. 5D. 64.某单位有职工750人，其中青年职工350人，中年职工250人，老年职工150人.为了了解该单位职工的健康情况，决定采用分层抽样的方法，从中抽取容量为15的样本.则从上述各层中依次抽取的人数分别是（）A. 8，4，3B. 6，5，4C. 7，5，3D. 8，5，25. 某协会有200名会员，现要从中抽取40名会员作样本，采用系统抽样法等间距抽取样本，将全体会员随机按1~200编号，并按编号顺序平均分为40组（1－5号，6－10号，…，196－200号）.若第5组抽出的号码为22，则第1组至第3组抽出的号码依次是（）A. 3，8，13B. 2，7，12C. 3，9，15D. 2，6，126.一个容量为n的样本,分成若干组,已知某组的频数和频率分别是40,0.125,则n的值为A. 640B.320C.240D. 1607.个容量为32的样本,已知某组样本的频率为0.125,则该组样本的频数为.A. 2B. 4C. 6D. 8 ( )8.我校高中生共有2700人,其中高一年级900人,高二年级1200人,高三年级600人,现采取分层抽样法抽取容量为135的样本,那么高一、高二、高三各年级抽取的人数分别为( )A.45,75,15B. 45,45,45C.30,90,15D. 45,60,309.某单位有老年人28人,中年人54人,青年人81人,为了调查他们的身体状况的某项指标,需从他们中间抽取一个容量为36的样本,则老年人、中年人、青年人分别各抽取的人数是( )A. 6,12,18B. 7,11,19C. 6,13,17D. 7,12,1710.某班的78名同学已编号1,2,3,…,78,为了解该班同学的作业情况,老师收取了学号能被5整除的15名同学的作业本,这里运用的抽样方法是( ).A.简单随机抽样法B.系统抽样法C.分层抽样法D.抽签法11.某工厂生产A、B、C三种不同型号的产品,产品数量之比依次为2 ：3 ：5.现用分层抽n样方法抽出一个容量为n的样本,样本中A种型号产品有16件,那么此样本的容量12.某学校共有教师490人,其中不到40岁的有350人,40岁及以上的有140人,为了解普通话在该校教师中的推广普及情况,用分层抽样的方法,从全体教师中抽取一个容量为70人的样本进行普通话水平测试,其中不到40岁的教师中应抽取的人数是___________.13．在某次学生考试的成绩中随机抽取若干学生的成绩，分组与各组的频数如下：[40,50),4；[50,60),1；[60,70),10；[70,80),11；[80,90),18；[90,100),6，估计本次考试的及格率为__________ . 14．把容量是100的样本分成8组，从第1组到第4组的频数分别是15，17，11，13，第5组到第7组的频率之和是0.32，那么第8组的频率是.15.《中华人民共和国道路交通安全法》 规定：车辆驾驶员血液酒精浓度在20~80 mg/100mL （不含80）之间，属于酒后驾车；血液酒精浓度在80mg/100mL （含80）以上时，属醉酒驾车。

2024学年八年级数学经典好题专项（频数分布表和频数分布直方图）练习一、选择题1、一组数据的最大值与最小值之差为80，若取组距为9，则分成的组数应是（ ） A. 7 B. 8 C. 9 D. 102、一个容量为80的样本，最大值是141，最小值是50，取组距为10，则可以分 （ ）A．10组 B．9组 C．8组 D．7组3、现有一组数据，最大值为93，最小值为22，现要把它分成6组，则下列组距中，合适的为 （ ） A. 9 B. 12 C. 15 D. 184、某棉纺厂为了了解一批棉花的质量，从中随机抽取了20根棉花纤维进行测量，其长度x (单位：mm)的数据分布如下表，则棉花纤维长度的数据在8≤x ＜32这个范围的频率为( )棉花纤维长度x频数 0≤x ＜8 1 8≤x ＜16 2 16≤x ＜24 8 24≤x ＜32 6 32≤x ＜403A.0.8 B ．0.7 C ．0.4 D ．0.25、小杰调查了本班同学的体重情况，画出频数直方图如图所示，下列结论中，错误的是( )A. 全班总人数为45人B. 体重在50～55 kg 的人数最多C. “45～50 kg ”这一组的频率比“60～65 kg ”这一组的大0.1D. 体重在60～65 kg 的人数占全班总人数的196、某一组数据中，已知最大值是84，最小值是52，若分成6组，且组距为整数，某组组中值为72.5，则这组数据可能是（ ）A. 51.5~57.5B. 69.5~75.5C. 68.5~76.5D. 70.5~74.57、为了了解本校八年级学生的体能情况，随机抽查了其中30名学生，测试了1分钟仰卧起坐的次数，并绘制成如图所示的频数分布直方图. 若25次为及格，则及格人数占总人数的（ ）A. 56.7%B. 90%C. 16.7%D. 33.3%8、为了解某校学生今年五一期间参加社团活动时间的情况，随机抽查了其中100名学生进行统计，并绘制成如图所示的频数直方图，已知该校共有1000名学生，据此估计，该校五一期间参加社团活动时间在8～10小时之间的学生数大约是（ ）A．280 B．240 C．300 D．260二、填空题9、一个样本有20个数据：35，31，33，35，37，39，35，38，40，39，36，34，35，37，36，32，34，35，36，34．在列频数分布表时，如果取组距为3，那么应分成 组10、有30个数据，其中最大值为40，最小值为15，若取组距为4，则应该分成 组11、有一个含有50个数据的数据组，已知最小数据是15，最大数据是45，且各数据都是整数，则这50个数据分为8组时，组距是________；若第1组的下限为14.5，则其上限为________，最末一组的上限为________.12、阅读对学生的成长有着深远的影响，某中学为了解学生每周课余阅读的时间，在本校随机抽取若干名学生进行调查，并依据调査结果绘制了如下不完整的统计表．则表中的a＝____.组别时间/时频数(人)频率A 0≤t≤0.560.15B 0.5≤t≤1 a 0.313、某中学抽取部分学生对“你最喜欢的球类运动”调查问卷，收集整理数据后列频数分布表（部分）如下：项目 乒乓球 羽毛球 篮球 足球频数 80 50百分比 40% 25% m则表格中m的值为14、某校在践行“社会主义核心价值观”演讲比赛中，对名列前20名的选手的综合分数m进行分组统计，结果如表所示，则a= ．组号 分组 频数一 6≤m＜7 2二 7≤m＜8 7三 8≤m＜9 a四 9≤m≤10 215、一个容量为60的样本，样本中最大值是172，最小值是150，取组距为3，则该样本可以分为 组16、小丽抽样调查了学校40名同学的体重（均精确到1kg），绘制了如图频数分布直方图，那么在该样本中体重不小于55kg的频率是 ．17、某地区中考现场考试内容有两项，50米跑为必考项目，另在立定跳远、坐位体前屈、实心球和一分钟跳绳中选一项测试．王老师对参加体育中考的九（1）班40名学生的一项选测科目作了统计，列出如图所示的统计表，则本班参加坐位体前屈的人数是 人．组别 立定跳远 坐位体前屈 实心球 一分钟跳绳频率 0.4 0.35 0.1 0.1518、空气质量指数，简称AQI，如果AQI在0～50空气质量类别为优，在51～100空气质量类别为良，在101～150空气质量类别为轻度污染，按照某市最近一段时间的AQI画出的频数分布直方图如图所示．已知每天的AQI都是整数，那么空气质量类别为优和良的天数占总天数的百分比为 %．19、将100个数据分成①～⑧组，如表所示：编号 ① ② ③ ④ ⑤ ⑥ ⑦ ⑧频数 4 8 12 24 18 7 3那么第④组的频数为 ．20、若小明统计了他家12月份打电话的通话时长，并列出频数分布表，则通话时长不超过10min的频率是 ．通话时长 x/min 0＜x≤5 5＜x≤10 10＜x≤15 x＞15频数（通话次数）20 16 20 4三、解答题21、体育委员统计了全班同学60s跳绳的次数，并列出频数表如下：次数 60≤x<80 80≤x<100 100≤x<120 120≤x<140 140≤x<160 160≤x<180频数 2 4 21 13 8 4 （1）全班共有多少名学生？（2）组距是多少？组数是多少？（3）跳绳次数在120≤x＜160范围内的学生有多少？22、每年的6月6日是全国爱眼日．某校为了做好全校2000名学生的眼睛保健工作，对学生的视力情况进行一次抽样调查．如图所示为利用所得的数据绘制的频数直方图(长方形的高表示该组人数)．请你根据图中提供的信息，回答下列问题：(1)本次调查共抽测了____名学生．(2)在这个问题中，样本是指_____________________．(3)视力在4.85～5.15这一组内的频数是_______．(4)如果视力小于4.85均属视力不良，那么该校约有_________名学生的视力不良，应给予治疗、矫正．23、为了了解某地九年级学生参加消防知识竞赛成绩（均为整数），从中抽取了1%的同学的竞赛成绩，整理后绘制了如下的频数直方图，请结合图形解答下列问题：（1）这个问题中的总体是 ；（2）竞赛成绩在84.5～89.5分这一小组的频率是 ；（3）若竞赛成绩在90分以上（含90分）的同学可以获得奖励，则估计该地获得奖励的九年级学生约有________人．24、在学校开展的综合实践活动中，某班进行了小制作评比，作品上交时间为5月1日至30日，评委会把同学们上交作品的件数按5天一组分组统计，绘制了频数直方图如下图所示，已知从左至右各长方形的高的比为2∶3∶4∶6∶4∶1，第三组的频数为12.请解答下列问题：(1)本次活动共有多少件作品参加评比？(2)哪组上交的作品数量最多？有多少件？(3)经过评比，第四组和第六组分别有10件，2件作品获奖，问：这两组哪一组获奖率较高？25、在开展“经典阅读”活动中，某校为了解全校学生利用课外时间阅读的情况，学校团委随机抽取若干名学生，调查他们一周的课外阅读时间，并根据调查结果绘制了如下尚不完整的统计图表．根据图表信息回答下列问题：(1)填空：a＝____，b＝____，m＝____，n＝____．(2)将频数直方图补充完整．(3)若该校有3000名学生，请根据上述调查结果，估计该校学生一周的课外阅读时间不足3 h的人数．26、为了让地震受灾的儿童得到救助，某社区组织“献爱心手拉手”捐款活动，对社区部分捐款户数进行调查和分组统计后，将数据整理成如图所示的统计表和统计图（图中信息不完整）．已知A、B两组捐款户数的比为1：5．请结合以上信息解答下列问题．（1）a= ，本次调查样本的容量是 ；（2）补全“捐款户数分组统计表和捐款户数统计图1”；（3）若该社区共有1000户住户参与捐款，请根据以上信息估计，全社区捐款不少于300元的户数是 户．27、为了了解某次“小学生书法比赛”的成绩情况，随机抽取了30名学生的成绩进行统计，并将统计情况绘制成如图所示的频数直方图，已知成绩x(单位：分)均满足“50≤x＜100”．根据图中信息回答下列问题：(1)图中a的值为____．(2)绘制扇形统计图时，成绩x在“70≤x＜80”范围内所对应扇形的圆心角的度数为____．(3)此次比赛共有300名学生参加，若将“x≥80”的成绩记为“优秀”，则获得“优秀”的学生大约有____人．28、为庆祝中华人民共和国成立70周年，郑州市某校组织八年级学生进行“方阵表演”．为了整齐划一，需了解学生的身高，现随机抽取该校八年级学生进行抽样调查，根据所得数据绘制出如下统计图表根据图表提供的信息，回答下列问题：（1）这次抽样调查，一共抽取学生 人；（2）扇形统计图中，扇形E的圆心角度数是 ；（3）请补全频数分布直方图；（4）已知该校八年级共有学生400人，请估计身高在160≤x＜170的学生约有多少人？参考答案一、选择题1、一组数据的最大值与最小值之差为80，若取组距为9，则分成的组数应是（ C ）A. 7B. 8C. 9D. 102、一个容量为80的样本，最大值是141，最小值是50，取组距为10，则可以分 （ A ）A．10组 B．9组 C．8组 D．7组3、现有一组数据，最大值为93，最小值为22，现要把它分成6组，则下列组距中，合适的为 （ B ）A. 9B. 12C. 15D. 184、某棉纺厂为了了解一批棉花的质量，从中随机抽取了20根棉花纤维进行测量，其长度x(单位：mm)的数据分布如下表，则棉花纤维长度的数据在8≤x＜32这个范围的频率为(A)棉花纤维长度x 频数0≤x＜8 18≤x＜16 216≤x＜24824≤x＜32 632≤x＜40 3A.0.8 B．0.7 C．0.4 D．0.25、小杰调查了本班同学的体重情况，画出频数直方图如图所示，下列结论中，错误的是(C )A. 全班总人数为45人B. 体重在50～55 kg 的人数最多C. “45～50 kg ”这一组的频率比“60～65 kg ”这一组的大0.1D. 体重在60～65 kg 的人数占全班总人数的19 【解】 8＋10＋14＋8＋5＝45(人)，故A 选项正确． 体重在50～55 kg 的人数有14人，最多，故B 选项正确． “45～50 kg ”这一组的频率是10÷45＝29， “60～65 kg ”这一组的频率是5÷45＝19， 29－19＝19≠0.1，故C 选项错误．5÷45＝19，故D 选项正确． 故选C.6、某一组数据中，已知最大值是84，最小值是52，若分成6组，且组距为整数，某组组中值为72.5，则这组数据可能是（ B ） A. 51.5~57.5 B. 69.5~75.5 C. 68.5~76.5 D. 70.5~74.57、为了了解本校八年级学生的体能情况，随机抽查了其中30名学生，测试了1分钟仰卧起坐的次数，并绘制成如图所示的频数分布直方图. 若25次为及格，则及格人数占总人数的（ A ）A. 56.7%B. 90%C. 16.7%D. 33.3%8、为了解某校学生今年五一期间参加社团活动时间的情况，随机抽查了其中100名学生进行统计，并绘制成如图所示的频数直方图，已知该校共有1000名学生，据此估计，该校五一期间参加社团活动时间在8～10小时之间的学生数大约是（ ）A．280 B．240 C．300 D．260【解答】解：由题可得，抽查的学生中参加社团活动时间在8～10小时之间的学生数为100﹣30﹣24﹣10﹣8＝28（人），∴1000280（人），即该校五一期间参加社团活动时间在8～10小时之间的学生数大约是280人．故选：A．二、填空题9、一个样本有20个数据：35，31，33，35，37，39，35，38，40，39，36，34，35，37，36，32，34，35，36，34．在列频数分布表时，如果取组距为3，那么应分成 4 组10、有30个数据，其中最大值为40，最小值为15，若取组距为4，则应该分成 7 组11、有一个含有50个数据的数据组，已知最小数据是15，最大数据是45，且各数据都是整数，则这50个数据分为8组时，组距是________；若第1组的下限为14.5，则其上限为________，最末一组的上限为________.[解析] 45－15＝30，3＜30÷8＜4，∴组距应为4.若第1组的下限为14.5，则其上限为14.5＋4＝18.5；最末一组的上限为14.5＋4×8＝14.5＋32＝46.5.[答案] 418.546.512、阅读对学生的成长有着深远的影响，某中学为了解学生每周课余阅读的时间，在本校随机抽取若干名学生进行调查，并依据调査结果绘制了如下不完整的统计表．则表中的a＝____.组别时间/时频数(人)频率A 0≤t≤0.560.15B 0.5≤t≤1 a 0.3【解析】∵被调查的总人数为6÷0.15＝40(人)，∴B组的人数为40×0.3＝12(人)，即a＝12.13、某中学抽取部分学生对“你最喜欢的球类运动”调查问卷，收集整理数据后列频数分布表（部分）如下：项目 乒乓球 羽毛球 篮球 足球频数 80 50百分比 40% 25% m则表格中m的值为 10%14、某校在践行“社会主义核心价值观”演讲比赛中，对名列前20名的选手的综合分数m进行分组统计，结果如表所示，则a= 9 ．组号 分组 频数一 6≤m＜7 2二 7≤m＜8 7三 8≤m＜9 a四 9≤m≤10 215、一个容量为60的样本，样本中最大值是172，最小值是150，取组距为3，则该样本可以分为 8 组16、小丽抽样调查了学校40名同学的体重（均精确到1kg），绘制了如图频数分布直方图，那么在该样本中体重不小于55kg的频率是 ．【解答】解：观察直方图可知：因为该样本中体重不小于55kg的频数为：9+5+2＝16，所以该样本中体重不小于55kg的频率是0.4．故答案为：0.4．17、某地区中考现场考试内容有两项，50米跑为必考项目，另在立定跳远、坐位体前屈、实心球和一分钟跳绳中选一项测试．王老师对参加体育中考的九（1）班40名学生的一项选测科目作了统计，列出如图所示的统计表，则本班参加坐位体前屈的人数是 人．组别 立定跳远 坐位体前屈 实心球 一分钟跳绳频率 0.4 0.35 0.1 0.15【解答】解：∵频率，∴频数＝频率×总数＝0.35×40＝14人．故答案为14．18、空气质量指数，简称AQI，如果AQI在0～50空气质量类别为优，在51～100空气质量类别为良，在101～150空气质量类别为轻度污染，按照某市最近一段时间的AQI画出的频数分布直方图如图所示．已知每天的AQI都是整数，那么空气质量类别为优和良的天数占总天数的百分比为 %．【解答】解：空气质量类别为优和良的天数占总天数的百分比为100%＝80%， 故答案为：80．19、将100个数据分成①～⑧组，如表所示：编号 ① ② ③ ④ ⑤ ⑥ ⑦ ⑧频数 4 8 12 24 18 7 3那么第④组的频数为 24．【解答】解：由题意可得，第④组的频数为：100﹣4﹣8﹣12﹣24﹣18﹣7﹣3＝24，故答案为：24．20、若小明统计了他家12月份打电话的通话时长，并列出频数分布表，则通话时长不超过10min的频率是 0.6 ．通话时长 x/min 0＜x≤5 5＜x≤10 10＜x≤15 x＞15频数（通话次数）20 16 20 4三、解答题21、体育委员统计了全班同学60s跳绳的次数，并列出频数表如下：次数 60≤x<80 80≤x<100 100≤x<120 120≤x<140 140≤x<160 160≤x<180频数 2 4 21 13 8 4 （1）全班共有多少名学生？（2）组距是多少？组数是多少？（3）跳绳次数在120≤x＜160范围内的学生有多少？解：（1）全班共有2＋4＋21＋13＋8＋4＝52（名）学生．（2）组距是80－60＝20次，组数是6.（3）跳绳次数在120≤x＜160范围内的学生有13＋8＝21（人）．22、每年的6月6日是全国爱眼日．某校为了做好全校2000名学生的眼睛保健工作，对学生的视力情况进行一次抽样调查．如图所示为利用所得的数据绘制的频数直方图(长方形的高表示该组人数)．请你根据图中提供的信息，回答下列问题：(1)本次调查共抽测了__160__名学生．(2)在这个问题中，样本是指__160名学生的视力情况__．(3)视力在4.85～5.15这一组内的频数是__40__．(4)如果视力小于4.85均属视力不良，那么该校约有__1250__名学生的视力不良，应给予治疗、矫正．23、为了了解某地九年级学生参加消防知识竞赛成绩（均为整数），从中抽取了1%的同学的竞赛成绩，整理后绘制了如下的频数直方图，请结合图形解答下列问题：（1）这个问题中的总体是 ；（2）竞赛成绩在84.5～89.5分这一小组的频率是 ；（3）若竞赛成绩在90分以上（含90分）的同学可以获得奖励，则估计该地获得奖励的九年级学生约有________人．解（1）某地九年级学生参加消防知识竞赛的成绩（2）＝0.32.（3）该地九年级获得奖励的人数约是（13＋7）÷1%＝2000（人）24、在学校开展的综合实践活动中，某班进行了小制作评比，作品上交时间为5月1日至30日，评委会把同学们上交作品的件数按5天一组分组统计，绘制了频数直方图如下图所示，已知从左至右各长方形的高的比为2∶3∶4∶6∶4∶1，第三组的频数为12.请解答下列问题： (1)本次活动共有多少件作品参加评比？ (2)哪组上交的作品数量最多？有多少件？(3)经过评比，第四组和第六组分别有10件，2件作品获奖，问：这两组哪一组获奖率较高？【解】 (1)12÷42＋3＋4＋6＋4＋1＝60(件)．(2)第四组上交的作品数量最多，有12×64＝18(件)．(3)第四组的获奖率为1018＝59，第六组的获奖率为2÷⎝⎛⎭⎫12×14＝23＝69. ∵59<69，∴第六组获奖率较高．25、在开展“经典阅读”活动中，某校为了解全校学生利用课外时间阅读的情况，学校团委随机抽取若干名学生，调查他们一周的课外阅读时间，并根据调查结果绘制了如下尚不完整的统计图表．根据图表信息回答下列问题：(1)填空：a ＝____，b ＝____，m ＝____，n ＝____． (2)将频数直方图补充完整．(3)若该校有3000名学生，请根据上述调查结果，估计该校学生一周的课外阅读时间不足3 h 的人数．【解】 (1)∵b ＝18÷0.12＝150，∴n ＝36÷150＝0.24，∴m ＝1－0.12－0.3－0.24－0.14＝0.2，∴a＝0.2×150＝30.(2)补全频数直方图如解图中斜纹所示．(3)3000×(0.12＋0.2)＝960.答：估计该校学生一周的课外阅读时间不足3 h的人数为960.26、为了让地震受灾的儿童得到救助，某社区组织“献爱心手拉手”捐款活动，对社区部分捐款户数进行调查和分组统计后，将数据整理成如图所示的统计表和统计图（图中信息不完整）．已知A、B两组捐款户数的比为1：5．请结合以上信息解答下列问题．（1）a= ，本次调查样本的容量是 ；（2）补全“捐款户数分组统计表和捐款户数统计图1”；（3）若该社区共有1000户住户参与捐款，请根据以上信息估计，全社区捐款不少于300元的户数是 户．解：（1）B组捐款户数是10，则A组捐款户数为10×=2，样本容量为（2+10）÷（1﹣8%﹣40%﹣28%）=50.（2）统计表C、D、E 组的户数分别为20，14，4．组别 捐款额（x）元 户数A 1≤x＜50 aB 100≤x＜200 10C 200≤x＜300 20D 300≤x＜400 14E x≥400 4（3）估计全社区捐款不少于300元的户数是1000×（28%+8%）=360（户）.27、为了了解某次“小学生书法比赛”的成绩情况，随机抽取了30名学生的成绩进行统计，并将统计情况绘制成如图所示的频数直方图，已知成绩x(单位：分)均满足“50≤x ＜100”．根据图中信息回答下列问题： (1)图中a 的值为____．(2)绘制扇形统计图时，成绩x 在“70≤x ＜80”范围内所对应扇形的圆心角的度数为____． (3)此次比赛共有300名学生参加，若将“x ≥80”的成绩记为“优秀”，则获得“优秀”的学生大约有____人．【解】 (1)a ＝30－(2＋12＋8＋2)＝6，故a ＝6.(2)成绩x 在“70≤x ＜80”范围内所对应扇形的圆心角的度数为360°×1230＝144°. (3)获得“优秀”的学生大约有300×8＋230＝100(人)．28、为庆祝中华人民共和国成立70周年，郑州市某校组织八年级学生进行“方阵表演”．为了整齐划一，需了解学生的身高，现随机抽取该校八年级学生进行抽样调查，根据所得数据绘制出如下统计图表根据图表提供的信息，回答下列问题： （1）这次抽样调查，一共抽取学生 人； （2）扇形统计图中，扇形E 的圆心角度数是 ；（3）请补全频数分布直方图；（4）已知该校八年级共有学生400人，请估计身高在160≤x＜170的学生约有多少人？【解答】解：（1）这次抽样调查，一共抽取学生4÷10%＝40（人）；（2）扇形统计图中，扇形E的圆心角度数是36054°，故答案为：40；54°；（3）身高在160≤x＜170的人数为：40×20%＝8人，补全频数分布直方图如图所示；（4）400×45%＝180（人），答：估计身高在160≤x＜170的学生约有180人．。

频率分布直方图练习题1、根据《中华人民共和国道路交通安全法》，酒后驾车的血液酒精浓度在20~80mg/100mL（不含80）组距之间，而醉酒驾车的血液酒精浓度在80mg/100mL（含0.080）以上。

在某地区一周内，共查处500名酒后驾车和醉酒驾车的司机。

通过对这些司机血液中酒精含量的检测，得到了频率分布直方图。

根据直方图，可估算醉酒驾车的司机人数约为70人。

2、对100名学生进行随机抽样，测得他们的身高（单位cm）。

将身高分为区间[155,160)，[160,165)，[165,170)，[170,175)，[175,180)，[180,185)，并得到样本身高的频率分布直方图。

根据直方图，可以得到身高在170cm以上的学生人数为30人。

将身高在[170,175)，[175,180)，[180,185)三个区间内的学生分别记为A、B、C三组，从这三组中分层抽样选取6人，则从A、B、C三组中分别抽取的人数为2、2、2人。

3、某部门为了确定对某路段进行限速60km/h是否合理，对通过该路段的500辆汽车的车速进行检测，并将所得数据按照组距[40,50)，[50,60)，[60,70)，[70,80]分组，得到频率分布直方图。

根据直方图，可以得出这500辆汽车中车速低于限速的汽车有90辆。

4、某校从参加高三年级期末考试的学生中抽出60名学生，并统计了他们的历史成绩（成绩均为整数且满分为100分）。

将不低于50分的成绩分为五段，得到部分频率分布直方图。

根据直方图，历史成绩在[70,80)的学生人数为16人。

5、给定XXX青年歌手大奖赛上某位选手得分的茎叶图，去掉一个最高分和一个最低分后，所剩数据的方差为25.4.6、从某小学随机抽取100名同学，将他们的身高（单位：厘米）数据绘制成频率分布直方图。

根据直方图，可得到a=141.若要从身高在[120,130)，[130,140)，[140,150)三组内的学生中，用分层抽样的方法选取18人参加活动，则应从每组中分别选取6人。

3．2 频数分布直方图同步练习解题示范例某校课外活动小组为了解本校九年级学生的睡眠时间情况， 对学校若干名九年级学生的睡眠时间进行了抽查，将所得数据整理后，画出了频数分布直方图的一部分，如图3-1，已知图中从左至右前5个小组的频率分别是0.04，0.08，0.24，0.28，0.24，第二小组的频数为4．请回答下列问题：（1）这次被抽查的学生人数是多少？并请补全频数分布直方图．（2）被抽查的学生中，睡眠时间在哪个范围内的人数最多？ 这一范围内的人数是多少？（3）如果该学校有900名九年级学生，若合理睡眠时间范围为7≤t<9，那么请你估计一下这个学校九年级学生中睡眠时间在此范围内的人数是多少？方案（1）由等式“频率＝频数总数”，可求出总数．由各组频率之和为1， 可求出余下一组的频率，补全直方图．（2）补全直方图后，可以直接从图中观察出频率最高的一组，利用第（1）题中类似的方法求出对应的频数．（3）先计算出符合要求的频率之和， 然后乘学生总数，即得到所求频数．实施（1）∵第二小组的频数为4，频率为0.08，∴这次被抽查的学生人数是4÷0.08=50（人）．第六小组的频率为1-0.04-0.08-0.24-0.28-0.24=0.12，频数为0.12×50=6． 补全后的直方图略．（2）被抽查的学生睡眠时间在6≤t<7（第四小组）的人数最多．∵0.28×50=14（人），∴这一范围内的人数是14人．（3）∵第五、六两组的频率之和为0.24+0.12=0.36，∴0.36×900=324（人）．∴估计这个学校九年级学生中睡眠时间在7≤t<9的人数约为324人．反思要搞清楚频率、频数、总数三者的关系，并能灵活运用．要学会读直方图．课时训练1．如图是九（2）班同学的一次体验中每分钟心跳次数的频数分布直方图（次数均为整数）．已知该班只有5位同学的心跳每分钟75次．根据直方图，下列说法错误的是（）．（A）数据75落在第二小组（B）第四小组的频率为0．1（C）心跳在每分钟75次的人数占该班体检人数的1 12（D）数据75一定是中位数。

18.4 频数分布表与直方图同步训练2023-2024学年冀教版数学八年级下册一、单选题1．一次数学比赛中，成绩在90以上的人有12人，频率为0.2，则参加比赛的共有（）．A．40人B．50人C．60人D．70人2．已知数据√5，3.14，−√9，π2，√83，其中无理数出现的频率是（）A．0.2B．0.4C．0.6D．0.83．某学校有1000名九年级学生，要知道他们在学业水平考试中成绩为A等、B等、C等、D等的人数各是多少，需要做的工作是（）A．求平均成绩B．进行频数分布C．求极差D．计算方差4．现将一组数据：25，21，23，25，27，29，25，28，30，29，26，24，25，27，26，22，24，25，26，28分成五组，其中第四组26.5～28.5的频数是() A．0.2B．3C．4D．55．已知一组数据：6，7，8，8，8，9，9，9，10，10，10，10，10，11，11，11，12，12，12，13，若以2为组距，则可以分成（）A．6组B．5组C．4组D．3组6．某次考试中，某班级的数学成绩统计图如右，下列说法错误的是（）A．得分在90~100分之间的人数最少B．该班的总人数为40人C．及格（≥60分）人数是38人D．得分在70~80分之间的人数最多7．为了更好地掌握国民经济发展水平，尤其是我国的人口发展水平，国务院制定了在2022年进行第八次人口普查方案，为了解全国各省份人口数占全国人口数的百分比，最适合使用的统计图是（）A．折线统计图B．扇形统计图C．条形统计图D．频数分布直方图8．对赵中、安中的最近的联考二的数学测试成绩(得分为整数)进行统计，将所有成绩由低到高分成五组，并绘制成如图所示的频数分布直方图，根据直方图提供的信息，在这次测试中，成绩为A等(80分以上，不含80分)的百分率为（）A．24%B．40%C．42%D．50%二、填空题9．对一组数据进行分组分析时，若其中分的一组为21≤a<41，则组中值为．10．在一个不透明的口袋中装有红球和白球共15个，这些球除颜色外都相同，将口袋中的球搅匀后，摸到红球的频率是40%，则口袋中红球约有个．11．一组数据的最大值为169，最小值为143，在绘制频数直方图时要求组距为3，则组数为．12．已知样本21，21，22，23，24，24，25，25，25，25，25，26，26，26，27，27，28，28，29，29，30．若组距为2，那么应分得的组数是．13．将100个数据分成8个组，如下表，则第六组的频数为．组号12345678第1页共6页◎第2页共6页14．统计某天7:00∼9:00经过某高速公路某测速点的汽车速度，得到如右所示的频数直方图（每一组不含前一个边界值，含后一个边界值）．若该路段汽车限速为120km/h （含），则超速行驶的汽车占全部汽车的%．三、解答题15．青少年视力水平下降已引起全社会的广泛关注，为了解某市初中毕业年级5000名学生的视力情况，我们从中抽取了一部分学生的视力作为样本进行数据处理，得到如下的不完整的频数分布表和频数分布直方图：请根据以上图表信息回答下列问题：（1）在频数分布表中，a=________,b=________；（2）补全条形统计图；（3）若视力在4.6以上（含4.6）均属正常，根据上述信息估计全区初中毕业生中视力正常的学生有多少？16．某校七年级1班体育委员统计了全班同学60秒跳绳的次数，并绘制出如下频数分布表和频数分布直方图：结合图表完成下列问题：（1）a=；（2）补全频数分布直方图；（3）写出全班人数是，并求出第三组“120≤x＜140”的频率（精确到0.01）（4）若跳绳次数不少于140的学生成绩为优秀，则优秀学生人数占全班总人数的百分之几？17．为庆祝中华人民共和国成立70周年，某校组织八年级学生进行“方阵表演”．为了整齐划一，需了解学生的身高，现随机抽取该校八年级部分学生进行调查，根据所得数据绘制出如下统计图表：第3页共6页◎第4页共6页第5页 共6页 ◎ 第6页 共6页根据图表提供的信息，回答下列问题：（1）这次抽样调查，一共抽取学生人，请补全频数分布直方图； （2）扇形统计图中，扇形E 的圆心角度数是；（3）已知该校八年级共有学生400人，请估计身高在160≤x <170的学生约有多少人？18．某中学积极开展跳绳锻炼，一次体育测试后，体育委员统计了全班同学单位时间的跳绳次数，列出了频数分布表和频数分布直方图，如图： 次数 频数 60≤x ＜8080≤x ＜1004100≤x ＜120 18 120≤x ＜140 13 140≤x ＜160 8 160≤x ＜180 180≤x ＜200 1（1）补全频数分布表和频数分布直方图； （2）样本数据中组距是 ，组数是 ；（3）若规定跳绳次数不低于140次为优秀，求全班同学跳绳的优秀率是多少？。