向量法求空间点到平面的距离

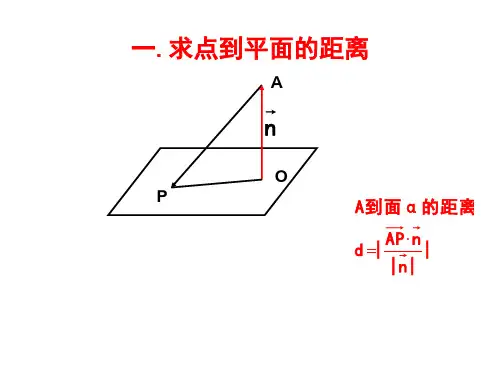
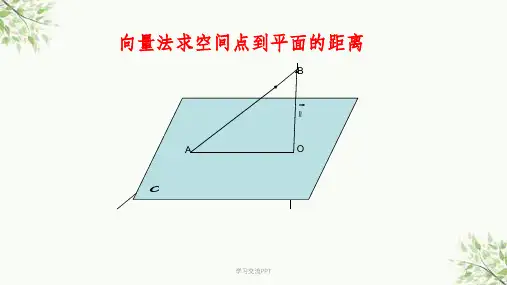
点到平面距离公式向量推导过程点到平面的距离是根据点到平面最近的一点和该点之间的距离来计算的。

假设平面的方程为Ax+By+Cz+D=0，点P的坐标为(x0,y0,z0)。

我们可以用向量的方式推导点到平面的距离公式。

1.首先，我们可以用平面上的两个向量a和b的向量积来表示平面的法向量n。

设平面上的两个点为P1(x1,y1,z1)和P2(x2,y2,z2)，则向量a 可以表示为a=P1P2=(x2-x1,y2-y1,z2-z1)，向量b可以表示为b=PN=(x0-x1,y0-y1,z0-z1)。

根据向量积的性质，平面的法向量n可以表示为n=a×b。

2. 接下来，我们需要求出点P到平面的最近点Q的坐标(xq, yq, zq)。

根据平面的法向量n和点P到Q的向量QP的向量积为零，即n · QP = 0。

向量QP可以表示为QP = PQ = (xq - x0, yq - y0, zq - z0)。

将向量n和向量QP带入上述等式，我们可以得到：n · QP = (x2 - x1, y2 - y1, z2 - z1) · (xq - x0, yq - y0, zq - z0) = 03.将上述等式展开，我们可以得到三个方程：(x2 - x1)(xq - x0) + (y2 - y1)(yq - y0) + (z2 - z1)(zq - z0) = 0x2(xq - x0) - x1(xq - x0) + y2(yq - y0) - y1(yq - y0) +z2(zq - z0) - z1(zq - z0) = 0x2xq - x2x0 - x1xq + x1x0 + y2yq - y2y0 - y1yq + y1y0 + z2zq - z2z0 - z1zq + z1z0 = 04.移项整理上述方程，得到：(x2 - x1)xq + (y2 - y1)yq + (z2 - z1)zq = x2x0 + y2y0 + z2z0 - x1x0 - y1y0 - z1z05.根据平面的法向量和平面上的一点可以表示平面的方程，我们可以得到：n·P=(x2-x1,y2-y1,z2-z1)·(x0,y0,z0)=Ax0+By0+Cz0-(Ax1+By1+Cz1)6. 由于平面上的最近点Q与平面上的一点P位于同一条直线上，所以点Q也满足平面的方程。

点到平面距离公式向量推导过程点到平面的距离是指从点到平面上的最短距离，即垂直于平面的线段的长度。

我们可以通过向量的投影来推导点到平面的距离公式。

设平面上一点为A，法向量为n，空间内一点为P。

假设P到平面的垂足为H，连接PH，有以下向量关系：1.向量PH垂直于平面：PH⋅n=02.向量AP平行于平面：AP⋅n=03.向量AH垂直于平面：AH⋅n=0根据上述向量关系，我们可以求得向量PH。

首先，假设平面上一点A为原点，两个平面内的向量可以用坐标表示，向量PH可表示为向量P减去向量H：PH=P-H根据第一条向量关系，我们知道PH⋅n=0，即(P-H)⋅n=0。

展开计算得：(P-H)⋅n=P⋅n-H⋅n=0我们知道H⋅n=0，即垂足H在平面上，所以上式变为：P⋅n=0这表示向量P平行于向量n，即向量P和向量n共线。

因此，可以设向量P=t⋅n，其中t为实数。

代入上式得：t⋅n⋅n=0n⋅n=0由于向量n不为零向量，n⋅n不为零，所以只有t=0，即向量P为零向量，也就是说向量P在平面上。

接下来我们计算向量AP：AP=A-P由于设点A为原点，所以A向量的坐标为(0,0,0)，代入上式得：AP=-P根据第二条向量关系，我们知道AP⋅n=0，即-P⋅n=0，进一步展开计算得：-P⋅n=0P⋅n=0和前面得到的结果相同，即向量P和向量n共线。

此时，我们可以得到向量P和向量n的夹角θ：cosθ = P⋅n / (，P，⋅，n，)因为向量n是单位向量，所以，n，=1，上式变为：cosθ = P⋅n / ，P根据余弦定理，cosθ = ，PH， / ，P，所以上式可以转化为：PH， = ，P，⋅cosθ这表示点到平面距离等于点P到垂足H的距离，也就是我们所要求的最短距离。

综上所述，点到平面的距离公式可以推导为：PH， = ，P，⋅cosθ其中，P为点的向量，n为平面的法向量，θ为点P和法向量n的夹角。

高考专题：向量法求空间的距离基础知识梳理(1)点到平面的距离(如图1)：平面α的法向量为n ，点P 是平面α外一点，点M 为平面α内任意一点，则点P 到平面α的距离d 就是MP 在向量n 方向射影的绝对值，即d =||||n n MP ⋅.(2)异面直线的距离(如图2)：设向量n 与两异面直线a 、b 都垂直，M ∈a 、P ∈b ，则两异面直线a 、b 间的距离d 就是MP 在向量n 方向射影的绝对值，即d =||||n n MP ⋅(3)线到平面的距离(如图3)：平面α∥直线l ，平面α的法向量为n ，点M ∈α、P ∈l ，平面α与直线l 间的距离d 就是MP 在向量n 方向射影的绝对值，即d =||||n n MP ⋅.(4)平面到平面的距离(如图4)：平面α∥β，平面α的法向量为n ，点M ∈α、P ∈β，平面α与平面β的距离d 就是MP 在向量n 方向射影的绝对值，即d =||||n n MP ⋅.图1nPM αb a图2n PMlαMPn图3β图4nPM αl典型例题剖析例1：如图，已知正方体1111D C B A ABCD -的棱长为1，求异面直线1AA 与1BD 的距离。

变式：如图，已知正方体1111D C B A ABCD -的棱长为1，求面对角线C B 1与体对角线1BD 的距离。

例2：在棱长为２的正方体1111ABCD A B C D -中，E 、F 分别是棱1111,A D A B 的中点． 求1B 到面EFBD 的距离ABCD1A 1B 1C 1D ABCD1A 1B 1C 1D变式：在直三棱柱ABC —A 1B 1C 1中，AB 1⊥BC 1，AB ＝CC 1＝a ，BC ＝b.(1)设E ，F 分别为AB 1，BC 1的中点，求证：EF ∥平面ABC ； (2)求证：A1C 1⊥AB ；(3)求B 1到平面ABC 1的距离．例3：三棱柱中，已知A BCD 是边长为1的正方形，四边形B B A A '' 是矩形，。

空间点到面距离公式向量法好的，以下是为您生成的文章：在咱们学习数学的奇妙世界里，有一个超实用的家伙，那就是空间点到面距离公式向量法！这玩意儿就像是一把神奇的钥匙，能帮咱们轻松打开好多几何难题的大门。

还记得我之前监考的一场考试，有一道题就是关于求空间点到面的距离。

当时大部分同学都愁眉苦脸的，抓耳挠腮，那场面真是让人又着急又觉得好笑。

其实啊，如果他们能把这个向量法给吃透，这道题根本就不在话下。

咱们先来说说这个向量法到底是啥。

简单来说，就是通过向量的运算来求出空间点到平面的距离。

假设平面的法向量为\(\vec{n}\)，平面上任意一点为\(P\)，要求距离的点为\(Q\)，那么点\(Q\)到平面的距离\(d\)就可以用公式\(d = \frac{|\vec{PQ} \cdot \vec{n}|}{|\vec{n}|}\)来计算。

可别被这一堆字母和符号给吓到啦！咱们来仔细琢磨琢磨。

比如说，有一个平面方程是\(Ax + By + Cz + D = 0\)，那它的法向量\(\vec{n}\)就可以表示为\((A,B,C)\)。

给大家举个例子哈。

假设平面方程是\(2x + 3y - z + 5 = 0\)，点\(Q(1,2,3)\)，咱们在平面上随便找一个点\(P(0,0,-5)\)，那\(\vec{PQ} = (-1,-2,8)\)。

平面的法向量\(\vec{n} = (2,3,-1)\)。

接下来算距离，先算\(\vec{PQ} \cdot \vec{n} = (-1)×2 + (-2)×3 + 8×(-1) = -2 - 6 - 8 = -16\)，\(|\vec{n}| = \sqrt{2^2 + 3^2 + (-1)^2} = \sqrt{14}\)。

所以距离\(d = \frac{|-16|}{\sqrt{14}} = \frac{16}{\sqrt{14}} =\frac{8\sqrt{14}}{7}\)。

法向量求点到面的距离公式在三维空间中，点到面的距离是一个非常常见的计算问题。

为了解决这个问题，我们可以使用法向量求解点到面的距离公式。

下面我们来逐步介绍这个公式的推导过程。

首先，我们需要知道什么是法向量。

在三维空间中，每一个平面都有一个垂直于该平面的向量，这个向量就被称为法向量。

它的方向指向平面的“外部”，也就是指向离平面最远的一侧。

现在，假设我们有一个平面，设平面上的一点为P，平面的法向量为N。

我们需要求解点P到平面的距离，记为d。

我们可以选取平面上的另外一个点Q，然后计算点P到点Q的距离，记为h。

根据勾股定理，我们有：h = PQ - d因为点Q在平面上，所以向量PQ一定与法向量N垂直。

因此，向量PQ可以拆分成两个分量，一个在法向量N上的投影，一个在平面上的投影。

设PQ的长度为L，那么它在法向量N上的投影为L cos θ，其中θ是法向量N与向量PQ的夹角。

于是，我们有：h = L cosθ将L cosθ带入上面的勾股定理中，得到：d = sqrt(PQ - h) = sqrt(PQ - L cosθ)现在的问题是如何求解L和θ。

我们可以通过向量点乘来计算向量PQ和法向量N之间的夹角θ，具体计算如下：cosθ = (PQ·N) / (|PQ| |N|)其中，PQ·N表示向量PQ和法向量N的点乘积，|PQ|和|N|分别表示向量PQ和法向量N的模长。

另外，PQ·N的结果也可以看作是向量PQ在法向量N上的投影，乘以向量PQ和法向量N的夹角的余弦值。

现在，我们已经得到了点到面的距离公式：d = sqrt(PQ - L cosθ)其中，PQ和N的值可以通过平面上的两个点坐标计算得到，cos θ可以通过向量点乘计算得到。

这个公式可以很方便地应用到实际问题中，例如碰撞检测、物体之间的距离计算等。

点到面的距离法向量
点到面的距离法向量是指从给定点到平面上的最短距离的方向向量。

要计算点到面的距离法向量，可以使用以下步骤：
1. 计算给定点到平面的距离，可以使用点到平面的距离公式：distance = |ax + by + cz + d| / √(a^2 + b^2 + c^2)，其中(a, b, c)是平面的法向量，(x, y, z)是给定点的坐标，d是平面的常数项。

2. 根据点到平面的距离公式，计算出点到平面的距离。

3. 将平面的法向量归一化，即将其长度调整为1。

4. 乘以距离的负值，以得到点到面的距离法向量。

这是因为距离的负值是指向平面外部的方向。

因此，点到面的距离法向量可以表示为：-distance * normalized_normal，其中normalized_normal是平面法向量的归一化向量。

向量法求点到面的距离介绍在三维空间中，向量法是一种常用的方法来求解点到面的距离。

点到面的距离是指从一个点到一个平面的最短距离。

该方法通过定义向量来计算点到面的距离，通过求解向量的垂直分量实现。

基本原理点到面的距离的基本原理是利用一个向量，从点出发到达平面上的任意一点，然后通过计算该向量在平面法向量上的投影来求解距离。

步骤Step 1: 确定平面的法向量首先，我们需要明确平面的法向量，法向量对于描述平面的方向非常重要。

如果平面已经被定义，法向量通常是已知的；否则，我们需要根据平面上的三个非共线点来计算出法向量。

Step 2: 确定点到平面上的一点我们需要选择一个点，该点将成为我们到平面上距离的参考点。

可以选择平面上的任意一点作为参考点，这取决于具体情况。

Step 3: 计算点到平面的向量通过使用参考点和平面上的一点，我们可以计算出从点到平面的向量。

这个向量的起点是点，终点是平面上的任意一点。

Step 4: 计算向量在法向量上的投影通过计算点到平面向量在法向量上的投影，我们可以得到点到平面的距离。

投影的计算方法是将向量与法向量进行点乘。

Step 5: 求解距离最后，通过计算得到的投影长度，我们可以得到点到平面的最短距离。

这就是点到面的距离。

示例示例平面方程我们假设有一个平面，方程为：x + y + z = 1。

示例点坐标我们选择一个点的坐标为：(2, -1, 3)。

示例步骤1.确定法向量：根据平面方程，法向量为 (1, 1, 1)。

2.确定参考点：我们选择 (0, 0, 1) 作为参考点，但可以选择其他任意点。

3.计算点到平面的向量：从点 (2, -1, 3) 到参考点 (0, 0, 1) 的向量为 (-2, 1, 2)。

4.计算向量在法向量上的投影：将向量 (-2, 1, 2) 与法向量 (1, 1, 1) 进行点乘得到投影长度 1。

5.求解距离：由于投影长度为 1，点 (2, -1, 3) 到平面的距离为 1。

用法向量求点到平面的距离公式用法向量求点到平面的距离公式是指通过一个平面的法向量和一个点与该平面的距离公式来计算点到平面的距离。

这个公式可以通过以下的方法得到：假设该平面的法向量为N，点P的坐标为(x0, y0, z0)，并设平面上任意一点为Q，则点P到平面的距离即为直线PQ在法向量N上的投影即点P到平面的距离为：
d = |(P-Q)·N| / |N|
其中，| |表示向量的模，·表示点积。

这个公式的意义就是点P到平面的距离等于点P到平面上任意一点的距离在平面法向量上的投影。

因此，只需要求出平面的法向量和平面上任意一点的坐标，就可以应用这个公式来求解点到平面的距离了。

向量法求点到面的距离一、前言在三维空间中，点到面的距离是一个非常重要的问题。

它在计算机图形学、计算机视觉等领域都有广泛的应用。

本文将介绍向量法求点到面的距离。

二、向量法原理假设有一个平面，其法向量为 $\vec{n}$，过该平面上一点 $P_0$ 的垂线方程为：$$\vec{n}\cdot(\vec{r}-\vec{P_0})=0$$其中 $\vec{r}$ 为任意一点的位置向量。

设点 $Q$ 到该平面的距离为 $h$，则有：$$h=\frac{\vec{n}\cdot(\vec{Q}-\vec{P_0})}{|\vec{n}|}$$三、求解过程1. 确定平面法向量 $\vec{n}$设已知三角形 $ABC$ 的三个顶点坐标分别为 $(x_A,y_A,z_A)$，$(x_B,y_B,z_B)$ 和 $(x_C,y_C,z_C)$，则可通过以下公式计算出平面法向量 $\vec{n}$：$$\begin{aligned}\vec{n}&=(x_B-x_A,y_B-y_A,z_B-z_A)\times(x_C-x_A,y_C-y_A,z_C-z_A)\\&=(y_B-y_A)(z_C-z_A)-(z_B-z_A)(y_C-y_A),\\&(z_B-z_A)(x_C-x_A)-(x_B-x_A)(z_C-z_A),\\&(x_B-x_A)(y_C-y_A)-(y_B-y_A)(x_C-x_A)\end{aligned}$$其中 $\times$ 表示向量叉乘。

2. 确定过点 $P$ 的垂线与平面的交点 $Q$过点 $P$ 的垂线方程为：$$\vec{n}\cdot(\vec{r}-\vec{P})=0$$将其与平面方程联立，解得：$$\begin{aligned}\vec{r}&=\vec{P}+\frac{\vec{n}\cdot(\vec{Q}-\vec{P})}{|\vec{n}|^2}\vec{n}\\&=\vec{P}+\frac{\vec{n}\cdot(\vec{ P_0}-\vec{P})}{|\vec{n}|^2}\vec{n}\end{aligned}$$其中 $\vec{Q}$ 为过点 $P$ 的垂线与平面的交点，$\vec{r}$ 为任意一点的位置向量。

点到平面的距离公式高中法向量点到平面的距离公式可以通过向量的方法进行求解。

首先，给定
平面的一般方程形式为Ax + By + Cz + D = 0，其中A、B、C为平面
的法向量的分量，而(x, y, z)为平面上任意一点的坐标。

假设平面上存在一点P（x1, y1, z1），我们需要求点P到平面的距离d。

为了方便计算，我们可以选择平面上一点Q，使得PQ与平面
垂直。

我们通过向量PQ与平面的法向量N的点乘来求解距离d，即：
d = |PQ · N| / |N|,
其中|PQ · N|表示向量PQ与N的点乘的模，|N|表示N的模长。

点乘的结果是一个标量，表示两个向量之间的夹角的余弦乘以两个向
量的模长的乘积。

当平面方程为Ax + By + Cz + D = 0时，平面的法向量为N = (A, B, C)。

拓展：
除了通过向量的方法求解点到平面的距离外，还可以使用点到平面的投影来求解。

点到平面的投影就是将点P垂直投影到平面上得到的点P'。

点P到平面的距离d就等于点P到点P'的距离。

点P'的坐标可以通过将点P带入平面方程得到。

然后，计算点P 与P'之间的距离即可得到点到平面的距离。

需要注意的是，如果平面是平行于坐标轴的，也可以直接计算点P 与平面的坐标分量的差值的绝对值，而不需要进行向量的运算。

利用向量法求点到平面的距离利用平面的法向量求点到平面的距离 甘肃省 彭长军 如图1，设n 是平面α的一个法向量，P 是α外一点，Q 是α内任意一点，则向量PQ u u u r 在法向量n 方向上的射影长d=PQ u u u r cos PQ,n <>uuu r u r =PQ n nu u u r r g r 就是点P 到平面α的距离.下面举几例予以说明.例1．已知A(2,3,1)、B(4,1,2)、C(6,3,7)、D(-5,-4,8)是空间不共面的四点,求点D 到平面ABC 的距离.解：设),,(z y x n =是平面ABC 的一个法向量，则由0n AB =g 及10n BC =g ,得2x 2y z 02x 2y 5z 0--+=⎧⎨++=⎩⇒2y x 32z x 3⎧=⎪⎪⎨⎪=-⎪⎩,取x=3,得)2,2,3(-=n ,于是点D 到平面ABC 的距离为d=DA n nu u u r r g r = 1749=171749. 例2．已知四边形ABCD 是边长为4的正方形，E 、F 分别是AB 和AD 的中点，GC ⊥平面ABCD ，且GC=2，求点B 到平面EFG 的距离.解：建立如图2所示的空间直角坐标系C-xyz ，则G(0,0,2),E(2,4,0),B(0,4,0), F(4, 2,0)，∴GE =(2,4,-2),GF =(4,2,-2),BE =(2,0,0).设平面EFG 的一个法向量为),,(z y x n =，则由0n GE =g 及0n GF =g ，得2x+4y 2z 04x 2y 2z 0-=⎧⎨+-=⎩⇒ x=y z 3y ⎧⎨=⎩,取y=1,得(1,1,3)n =,于是点B 到平面EFG 的距离为d=BE n n u u u r r g r =11112112=. 例3.在棱长为1的正方体ABCD-A 1B 1C 1D 1中，求点C 1到平面A 1BD 的距离。