△形与Y形电阻电路等效变换
- 格式:doc
- 大小:116.00 KB
- 文档页数:3

三角形和y型电路变换公式三角形和Y型电路变换公式一、引言电路是电子学的基础,而三角形和Y型电路是电路分析中常见的两种电路形式。
本文将介绍三角形和Y型电路的变换公式,以及它们在电路分析中的应用。
二、三角形电路变换公式1. 三角形到Y型的变换在电路分析中,有时需要将三角形电路转换为Y型电路以便进行更简单的分析。
三角形到Y型的变换公式如下:Ya = (Xb + Xc) / XaYb = (Xc + Xa) / XbYc = (Xa + Xb) / Xc其中,Xa、Xb、Xc分别代表三角形电路中的三个电阻。
2. Y型到三角形的变换同样地,有时需要将Y型电路转换为三角形电路以便进行更方便的分析。
Y型到三角形的变换公式如下:Xa = Yb*Yc / (Ya+Yb+Yc)Xb = Yc*Ya / (Ya+Yb+Yc)Xc = Ya*Yb / (Ya+Yb+Yc)其中,Ya、Yb、Yc分别代表Y型电路中的三个电导。
三、三角形和Y型电路的应用三角形和Y型电路的变换公式在电路分析中有着广泛的应用。
以下是一些常见的应用场景:1. 网络电路分析三角形和Y型电路变换公式可用于简化网络电路的分析。
通过将复杂的网络电路转换为三角形或Y型电路,可以更容易地计算电流、电压和功率等参数。
2. 电阻网络分析在电阻网络中,三角形和Y型电路的变换公式可以帮助我们快速计算电阻的等效值。
通过变换公式,我们可以将复杂的电阻网络简化为简单的三角形或Y型电路,进而计算等效电阻。
3. 电感和电容网络分析除了电阻网络,三角形和Y型电路的变换公式也适用于电感和电容网络的分析。
通过变换公式,我们可以将复杂的电感或电容网络转换为简单的三角形或Y型电路,进而进行更简单的分析。
四、结论三角形和Y型电路变换公式是电路分析中的重要工具,它们可以帮助我们简化电路的分析过程。
通过将复杂的电路转换为三角形或Y 型电路,我们可以更方便地计算电流、电压和功率等参数。
在电路分析中,我们可以根据具体情况选择使用三角形到Y型的变换或Y 型到三角形的变换,以便更好地解决问题。

y形电路和三角形电路等效变换Y形电路和三角形电路等效变换在电路中,有时候我们需要将一个电路转换成另一个电路,这个过程就叫做等效变换。
在电路中,Y形电路和三角形电路是两种常见的电路结构,它们之间可以进行等效变换。
Y形电路是由三个电阻器组成的电路,它们的连接方式形成了一个Y形结构。
三角形电路也是由三个电阻器组成的电路,它们的连接方式形成了一个三角形结构。
这两种电路结构在电路中都有广泛的应用。
在进行等效变换时,我们需要将Y形电路转换成三角形电路,或者将三角形电路转换成Y形电路。
这个过程需要根据电路的特点和电阻器的阻值来进行计算。
我们来看Y形电路和三角形电路之间的等效变换。
当我们将一个Y 形电路转换成一个三角形电路时,需要按照以下步骤进行:1. 将Y形电路中的电阻器R1和R2串联起来,得到一个新的电阻器R12。
2. 将Y形电路中的电阻器R2和R3串联起来,得到一个新的电阻器R23。
3. 将Y形电路中的电阻器R1和R3串联起来,得到一个新的电阻器R13。
4. 将新的电阻器R12、R23和R13连接起来,形成一个三角形电路。
这样,我们就将一个Y形电路转换成了一个等效的三角形电路。
同样地,当我们将一个三角形电路转换成一个Y形电路时,需要按照以下步骤进行:1. 将三角形电路中的电阻器R12和R23并联起来,得到一个新的电阻器R2。
2. 将三角形电路中的电阻器R23和R13并联起来,得到一个新的电阻器R3。
3. 将三角形电路中的电阻器R13和R12并联起来,得到一个新的电阻器R1。
4. 将新的电阻器R1、R2和R3连接起来,形成一个Y形电路。
这样,我们就将一个三角形电路转换成了一个等效的Y形电路。
在进行等效变换时,需要注意电路中的电阻器阻值是否相等。
如果电阻器阻值不相等,等效变换的结果可能会产生误差。
因此,在进行等效变换时,需要根据电路的实际情况进行计算。
Y形电路和三角形电路之间可以进行等效变换,这个过程需要根据电路的特点和电阻器的阻值来进行计算。

三角形和y型电路变换公式三角形和Y型电路变换公式在电路分析和电子工程中,三角形和Y型电路变换公式是一组重要的公式,用于将三角形电路转换为Y型电路或将Y型电路转换为三角形电路。
这些公式在电路分析和设计中具有广泛的应用,可以简化复杂电路的分析过程,提高电路设计的效率。
三角形电路是由三个电阻或阻抗组成的电路,它们呈三角形连接。
Y 型电路是由三个电阻或阻抗组成的电路,它们呈Y型连接。
三角形和Y型电路变换公式可以帮助我们在分析和设计电路时,通过变换电路连接方式,简化电路结构,使分析和计算更加简便。
我们来看看将三角形电路转换为Y型电路的变换公式。
假设三角形电路的三个电阻或阻抗分别为R1、R2和R3。
根据变换公式,我们可以得到以下关系:R1 = (Rab * Rac) / (Rab + Rac + Rbc)R2 = (Rab * Rbc) / (Rab + Rac + Rbc)R3 = (Rac * Rbc) / (Rab + Rac + Rbc)其中,Rab、Rac和Rbc分别表示三角形电路中的三个电阻或阻抗之间的等效电阻或阻抗。
通过这些公式,我们可以将给定的三角形电路转换为等效的Y型电路。
接下来,我们来看看将Y型电路转换为三角形电路的变换公式。
假设Y型电路的三个电阻或阻抗分别为R1、R2和R3。
根据变换公式,我们可以得到以下关系:Rab = (R1 * R2 + R2 * R3 + R3 * R1) / R1Rac = (R1 * R2 + R2 * R3 + R3 * R1) / R2Rbc = (R1 * R2 + R2 * R3 + R3 * R1) / R3通过这些公式,我们可以将给定的Y型电路转换为等效的三角形电路。
三角形和Y型电路变换公式的应用非常广泛。
在电路分析中,我们经常需要将复杂的电路转换为简化的形式,以便更好地理解和分析电路的行为。
利用三角形和Y型电路变换公式,我们可以将复杂的电路简化为更简单的形式,从而更方便地进行分析。


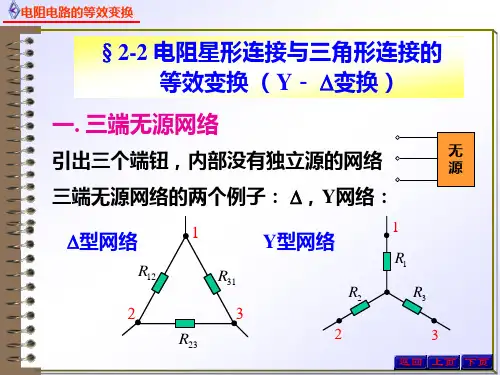
电阻星形和三角形连接的等效变换
1 、电阻星形和三角形连接的特点:星形联接或T 形联接,用符号Y 表示。
特点:三个电阻的一端联接在一个结点上,成放射状。
三角形联接或π形联接,用符号Δ表示。
三角形联接或π形联接,用符号Δ表示。
2 、电阻星形和三角形变换图:星形变换成三角形如图2-2-1(a) 所示,三角形连接变换成星形如图2-2-1(b) 所示。
图2-2-1(a) 图2-2-1(b)
3 、等效变换的条件:要求变换前后,对于外部电路而言,流入(出)对应端子的电流以及各端子之间的电压必须完全相同。
4 、等效变换关系:
#8226; 已知星形连接的电阻R A 、R B 、R C ,求等效三角形电阻R AB 、R BC 、R CA 。
,
公式特征:看下角标,两相关电阻的和再加上两相关电阻的积除以另一电阻的商。
#8226; 已知三角形连接的电阻R AB 、R BC 、R CA ,求等效星形电阻R A 、R B 、R C 。
,,
公式特征:看下角标,分子为两相关电阻的积,分母为三个电阻的和。
#8226; 特殊:当三角形(星形)连接的三个电阻阻值都相等时,变换后的三个阻值也应相等。
,。


组织教学:清点人数,强调课堂纪律。
复习提问:1.受控源可分为哪几类?2.什么是转移电阻?什么是转移电导?导入新课:线性电阻和直流电源组成的电路称为直流线性电阻电路,简称直流电阻电路。
许多现实应用中的电阻电路都相当复杂,所以学习一些基本的分析方法就显得非常重要,通过学习这些方法,在电力、电信和无线电技术中,有许多工程的实际问题,都可以归结为电阻电路的计算问题,本节课我们首先介绍电阻的等效转换方法。
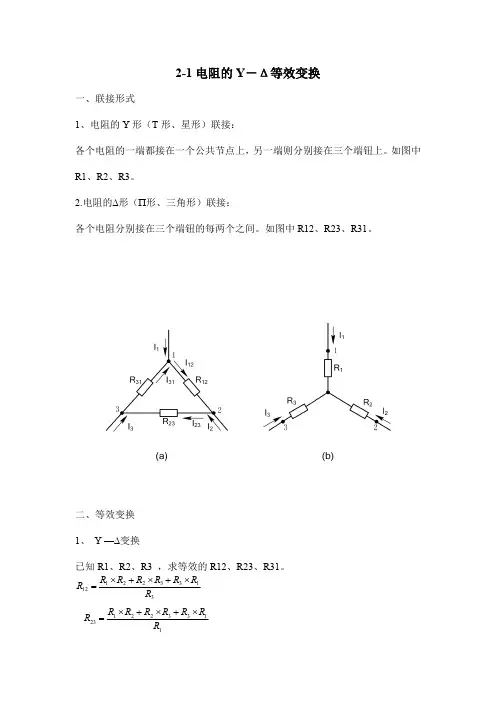
新授课:2-1电阻的Y-Δ等效变换一、联接形式1、电阻的Y形(T形、星形)联接:各个电阻的一端都接在一个公共节点上,另一端则分别接在三个端钮上。
如图中R1、R2、R3。
2.电阻的∆形(∏形、三角形)联接:各个电阻分别接在三个端钮的每两个之间。
如图中R12、R23、R31。
二、等效变换 1、 Y —∆变换已知R1、R2、R3 ,求等效的R12、R23、R31。
一般公式: 2、 ∆ —Y 变换:已知R12、R23、R31 ,求等效的R1、R2、R3 。
一般公式:313322112R R R R R R R R ⨯+⨯+⨯=113322123R R R R R R R R ⨯+⨯+⨯=213322131R R R R R R R R ⨯+⨯+⨯=对臂电阻单个相邻电阻之积的和=∆R 31231231121R R R R R R ++⨯=31231223122R R R R R R ++⨯=31231231233R R R R R R ++⨯=(a)(b)3、 特例,当三个电阻相等时: 课堂练习:1.下图2-10a 中的各个电阻阻值如图所示,求电路的等效电阻R ab 。
二.如图所示电路中, 已知U s=225V , R 0=1Ω, R 1=40Ω, R 2=36Ω, R 3=50Ω, R 4=55Ω, R 5=10Ω, 试求各电阻的电流。
周圈电阻之和相邻电阻之积=Y R ∆∆==R R R R Y Y 13或解 将△形连接的R 1, R 3, R 5等效变换为Y 形连接的R a, R c 、R d, 如图2.10(b)所示, 代入式(2.8)求得图2.10(b)是电阻混联网络, 串联的R c 、R 2的等效电阻R c2=40Ω, 串联的R d 、R 4的等效电阻R d4=60Ω, 二者并联的等效电阻R a 与R ob 串联, a 、b 间桥式电阻的等效电阻 桥式电阻的端口电流cb( a ) I I b( b )Ω=++⨯=++=Ω=++⨯=++=Ω=++⨯=++=5405010501044050101040204050104050135351355113513R R R R R R R R R R R R R R R R R R d c a Ω=+⨯=2460406040ab R Ω=+=442420i RR 2、R 4的电流各为 为了求得R 1、R 3、R 5的电流, 从图2.10(b)求得 回到图2.10(a )电路, 得 并由KCL 得小结:本节课我们学习重点在于电阻的星形和三角形连接之间的转换,同学们要熟练掌握两种连接方式的转换公式,做到从整体把握电路的化简方法。
a △形电路b Y形电路△形和Y形电路之间的相互变换也应满足外部特性相同的原则,直观地说:就是必须使任意两对应端钮间的电阻相等;具体地说,就是当第三端钮断开时,两种电路中每一对相对应的端钮间的总电阻应当相等;例如上图a和b中,当端钮3断开时,两种电路中端钮1、2间的总电阻相等,即R1+R2=R12R23+R31/R12+R23+R31 1同理有R2+R3=R23R31+R12/R12+R23+R31 2R3+R1=R31R12+R23/R12+R23+R31 3 将△形变换成Y形,即已知△形电路的R12、R23、R31,求Y形电路的R1、R2、R3;为此,将式1、2、3相加后除以2,可得R1+ R2+ R3= R23 R12+ R23R31+ R12 R31/R12+R23+R31 4 从式4中分别减去式1、2和式3,可得R1=R12R31/R12+R23+R31 5R2=R12R23/R12+R23+R31 6R3=R23R31/R12+R23+R317 以上三式就是△形电路变换为等效Y形电路的公式;三个公式可概括为R Y=△形中相邻两电阻的乘积/△形中电阻之和当R12=R23=R31=R△时,则R1= R2= R3=1/3 R△将Y形变换成△形,即已知Y形电路的R1、R2、R3,求△形电路的R12、R23、R31;为此,将式5、6和式7两两相乘后再相加,经化简后可得R1R2+ R2R3+ R3R1= R12R23 R31/R12+R23+R318 将式8分别除以式7、5和式6,可得R12 =R1+R2+ R1R2/R39R23 =R2+R3+ R2R3/R110R31 =R3+R1+ R3R1/R2 11 以上三式就是Y形电路变换为等效△形电路的公式;三个公式可概括为R△=Y形中两两电阻的乘积之和/Y形中对面的电阻当R12=R23=R31=R Y时,则R12= R23= R31=3 R Y应当指出,上述等效变换公式仅适用于无源三端式电路;。
三角形电阻和y形电阻转换公式
三角形电阻和Y形电阻是电路中常见的两种电阻连接方式。
它们可以相互转换,并且有特定的公式可以用于计算它们之间的等效电阻。
首先,我们来看一下三角形电阻的转换公式。
在一个三角形电阻连接中,三个电阻分别连接在三个角上,并且它们之间没有其他连接。
假设这三个电阻分别为R1、R2和R3。
那么三角形电阻的等效电阻Rt 可以用如下公式计算:
1/Rt = 1/R1 + 1/R2 + 1/R3
这个公式意味着,将三个电阻的倒数相加,然后再取倒数,就可以得到三角形电阻的等效电阻。
接下来,我们来看一下Y形电阻的转换公式。
在一个Y形电阻连接中,三个电阻分别连接在一个共点上,并且它们之间没有其他连接。
假设这三个电阻分别为R1、R2和R3。
那么Y形电阻的等效电阻Ry 可以用如下公式计算:
1/Ry = 1/R1 + 1/R2 + 1/R3
这个公式与三角形电阻的转换公式是相同的,只是名称不同而已。
需要注意的是,这些转换公式只适用于电阻之间没有其他连接的情况。
如果电路中存在其他元件或连接,这些公式可能不再适用。
希望以上解释能够满足您的需求,如果您还有其他问题,请随时提问。
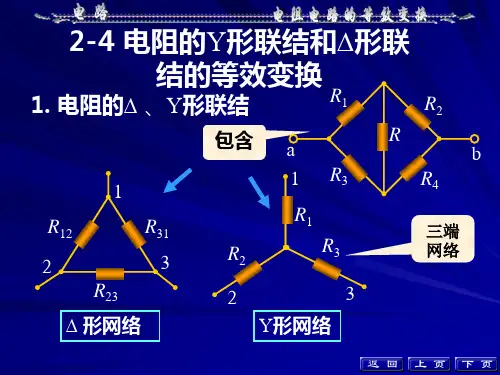
第二章-电阻电路的等效变第二章 电阻电路的等效变换2.1 学习要点1. 电阻的等效变换:电阻的串并联, Y 与△的等效变换。
2. 电源的串联、并联及等效变换。
3. “实际电源”的等效变换。
4. 输入电阻的求法。
2.2 内容提要 2.2.1 电阻的等效变换1. 电阻的串联:等效电阻: R eq =∑1=k nk R ;分压公式:u k =eqkeq ×R R u ; 2. 电阻的并联:等效电导:G eq =∑1=k nk G ;分流公式:qe G G i i keqk ×=;2.2.2. 电阻的Y 与△的等效变换1. △→Y :一般公式:Y 形电阻=形电阻之和形相邻电阻的乘积∆∆;即31232331*********231231212311++=++=++R R R R R R R R R R R R R R R R R R 2312=2. Y →△:一般公式:形不相邻电阻形电阻两两乘积之和形电阻=Y Y ∆;即:213322131113322123313322112++=++=++=R R R R R R R RR R R R R R R R R R R R R R R R2.2.3 电源的串联、并联等效变换 电源的串联、并联等效变换见表2.1。
表2.1 电源的串联、并联等效变换图2.2.4 “实际电源”的等效变换 1. “实际电压源”→“实际电流源” R i =R u 或 G i =1/R u i s =u s /R u 2. “实际电流源”→“实际电压源”R u =R i =1/G i u s =i s R i =i s /G i两者等效互换的原则是保持其端口的V AR 不变。
2.2.5 输入电阻的求法一端口无源网络输入电阻的定义(见图2.2):R in =u/ i1. 当一端口无源网络由纯电阻构成时,可用电阻的 串并联、Y 形与△形等效变换化简求得。
2. 当一端口无源网络内含有受控源时,可采用外加电压法或外加电流法求得: 即输入电阻R in =u s /i 或 R in =u/ i s方法是:在端口处加一电压源u s (或电流源i s ), 再求比值u s /i 或u/ i s ,该比值即是一端口无源网络的输入电阻。
y形电路和三角形电路等效变换在电路中,有时我们需要进行等效变换,以方便电路的分析和计算。
Y形电路和三角形电路是两种常见的等效变换方式,下面我们将分步骤介绍它们的原理和操作方法。
一、Y形电路和三角形电路的定义Y形电路和三角形电路都是由不同数量的电阻器组成的电路。
Y形电路是由三个电阻器组成,形状呈Y形。
其中,一个端子连接在公共点(电阻器之间的交点),另外三个端子连接在电阻器的另外三个端点。
三角形电路是由三个电阻器组成,形状呈三角形。
其中,每个电阻器的两个端点分别连接在三角形的三个顶点处。
二、Y形电路和三角形电路的等效变换Y形电路和三角形电路之间可以进行等效变换,即把一个Y形电路转换为一个三角形电路,或者把一个三角形电路转换为一个Y形电路。
这种变换可以使电路的分析更加容易和直接。
1. Y形电路变换为三角形电路把一个Y形电路变换为一个三角形电路的方法如下:(1)将Y形电路中的公共点和其中的一个端点连接起来,形成一个三角形。
(2)将其他两个端点连成一个电阻器。
(3)根据欧姆定律,可以算出三个电阻器等效后的电阻值。
2. 三角形电路变换为Y形电路把一个三角形电路变换为一个Y形电路的方法如下:(1)把一个电阻器上的两个端点连接到一个公共点上。
(2)将连接这个公共点的两个电阻器分别连接到这个电阻器的两个端点。
(3)根据欧姆定律,可以算出三个电阻器等效后的电阻值。
三、应用范围Y形电路和三角形电路的等效变换适用于各种电路分析和计算。
例如,通过这种变换可以将一些非常复杂的电路简化,从而方便进行分析和计算。
还可以用于模拟电路、计算机网络和通信电路等方面。
总之,Y形电路和三角形电路的等效变换是电路分析和计算中常用的一种方法。
通过这种方法,可以将复杂的电路简化为更为简单的形式,方便电路分析和设计。
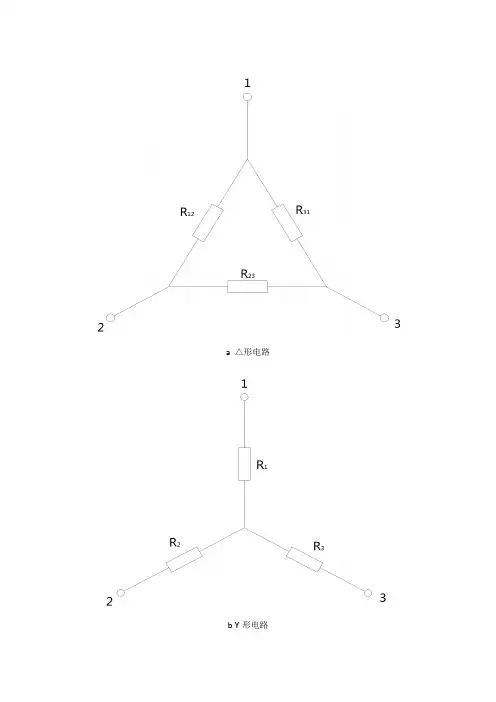
(a) △形电路
(b) Y形电路
△形和Y形电路之间的相互变换也应满足外部特性相同的原则,直观地说:就是必须使任意两对应端钮间的电阻相等。
具体地说,就是当第三端钮断开时,两种电路中每一对相对应的端钮间的总电阻应当相等。
例如上图(a)和(b)中,当端钮3断开时,两种电路中端钮1、2间的总电阻相等,即
R1+R2=R12(R23+R31)/(R12+R23+R31)
(1)
同理有
R2+R3=R23(R31+R12)/(R12+R23+R31)
(2)
R3+R1=R31(R12+R23)/(R12+R23+R31)
(3)
将△形变换成Y形,即已知△形电路的R12、R23、R31,求Y形电路的R1、R2、R3。
为此,将式(1)、(2)、(3)相加后除以2,可得
R1+ R2+ R3=( R23R12+ R23R31+ R12R31)/(R12+R23+R31) (4)
从式(4)中分别减去式(1)、(2)和式(3),可得
R1=R12R31/(R12+R23+R31)
(5)
R2=R12R23/(R12+R23+R31)
(6)
R3=R23R31/(R12+R23+R31)
(7)
以上三式就是△形电路变换为等效Y形电路的公式。
三个公式可概括为
R Y=△形中相邻两电阻的乘积/△形中电阻之和
当R12=R23=R31=R△时,则
R1= R2= R3=1/3 R△
将Y形变换成△形,即已知Y形电路的R1、R2、R3,求△形电路的R12、R23、R31。
为此,将式(5)、(6)和式(7)两两相乘后再相加,经化简后可得
R1R2+ R2R3+ R3R1= R12R23R31/(R12+R23+R31) (8)
将式(8)分别除以式(7)、(5)和式(6),可得
R12=R1+R2+ R1R2/R3 (9)
R23=R2+R3+ R2R3/R1 (10)
R31=R3+R1+ R3R1/R2 (11)
以上三式就是Y形电路变换为等效△形电路的公式。
三个公式可概括为
R△=Y形中两两电阻的乘积之和/Y形中对面的电阻
当R12=R23=R31=R Y时,则
R12= R23= R31=3 R Y
应当指出,上述等效变换公式仅适用于无源三端式电路。