电阻电路的等效变换.

第三页
特例：两电阻并联
Req
R1R2 R1 R2
i1
R2 R1 R2
i
i2
R1 R1 R2
i
二、电阻的混联 —串、并联的组合
采用逐次等效的办法
第四页
例2－1 求Rab=?
6 15
5
①
5
③
① Re'q R3 R4 10 ②
③
Req
R1
R '' eq
6 6
12
② R'' eq
电阻电路等效变换
第一页
§2-1电阻的串联和并联
一、串联 电阻首尾相联，流过同一电流的连接方式，称为串联(图2－2a)
VAR:
u u1 u2 un R1i R2i Rni (R1 R2 Rn )i
VAR: u Reqi
即若干电阻串联等效于一个电阻，Req=R1+R2+···+Rn
①等效变换法 Rin,Req的计算方法： ②根据Rin的定义
i u
图2－18a
i u
图2－18b
第十八页
例2－8 求图2-19电路的输入电阻 Rin=?
i
u
l2
l1
i1
i2
图2－19
解: 标明电压、电流及参考方向, 则:
u Rin i
选择回路 l1, 列写KVL: 3i2 4i2 2i1 0 i2 2i1
R3 R1
例2－5 求图2-9a电路中电流 I1, I2, I3 , I4。
I I2 I1
解: 思路 Δ→Y
Req I
I1
I2
I3
I4
48
Rb 4 4 8 2, 同理,求得 : Rc 2, Rd 1, Req (1 Rb ) //(5 Rd ) Rc 4

结论：若电路中两点电位相等，则： ①可将这两点短路 ② 可将这两点之间连接的支路断开 对某些对称性电路可采用此方法处理
例2－4 图2－7所示电路每个电阻都是2Ω, 求a, b两端的等效电阻
c
d
e
根据电路的对称性, 可知 c, d, e三点等电位, 故可用导线短接。
8 2 8 2 16 3 3 2 Req [(2 // 1) 2] //(2 // 1) 2 // 2 8 2 3 3 15 3 3
R12 ( R23 R31 ) R R 故： 1 2 R12 R23 R31
同理,令i1=0, 可得: R2 R3 同理,令i2=0, 可得: R3 R1 特例, 若R12=R23=R31=RΔ,则: R1=R2=R3=RY,且 RΔ=3RY 反之, 可得:
R23 ( R12 R31 ) R12 R23 R31 R31 ( R12 R23 ) R12 R23 R31
§2-2电阻的Y－Δ等效变换 R1, R2, R3 Y(星)形连接 R3, R4, R5 R1, R3, R4 Δ(三角)形连接 R2, R3, R5
} }
如何求该一端口的Req? 若Y→Δ,即 R1, R2, R3 →Ra, Rb, Rc, 则： Req =(Ra//R4+ Rb//R5,)//Rc 问题： 如何进行等效变换？保证伏安特性相同 i1 i1
§2-1电阻的串联和并联
一、串联 电阻首尾相联，流过同一电流的连接方式，称为串联(图2－2a)
VAR:
u u1 u2 un
VAR:
u Reqi
R1i R2i Rni ( R1 R2 Rn )i

第二章 电阻电路的等效变换2.1 学习要点1. 电阻的等效变换：电阻的串并联， Y 与△的等效变换。

2. 电源的串联、并联及等效变换。

3. “实际电源”的等效变换。

4. 输入电阻的求法。

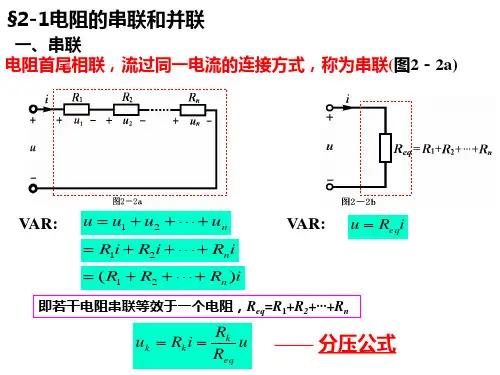
2.2 内容提要 2.2.1 电阻的等效变换1. 电阻的串联：等效电阻： R eq ＝∑1=k nk R ；分压公式：u k ＝eqkeq ×R R u ； 2. 电阻的并联：等效电导：G eq ＝∑1=knk G ；分流公式：qe G G i i keq k ×=； 2.2.2. 电阻的Y 与△的等效变换1. △→Y ：一般公式：Y 形电阻＝形电阻之和形相邻电阻的乘积∆∆；即31232331*********231231212311++=++=++R R R R R R R R R R R R R R R R R R 2312＝2. Y →△：一般公式：形不相邻电阻形电阻两两乘积之和形电阻＝Y Y ∆；图 2.1即：213322131113322123313322112++=++=++=R R R R R R R R R R R R R R R R R R R R R R R R2.2.3 电源的串联、并联等效变换 电源的串联、并联等效变换见表2.1。

表2.1 电源的串联、并联等效变换2.2.4 “实际电源”的等效变换 1. “实际电压源”→“实际电流源” R i ＝R u 或 G i ＝1/R u i s ＝u s /R u 2. “实际电流源”→“实际电压源”R u ＝R i ＝1/G i u s ＝i s R i ＝i s /G i两者等效互换的原则是保持其端口的V AR 不变。

2.2.5 输入电阻的求法一端口无源网络输入电阻的定义（见图2.2）：R in ＝u/ i1. 当一端口无源网络由纯电阻构成时，可用电阻的 串并联、Y 形与△形等效变换化简求得。

2. 当一端口无源网络内含有受控源时，可采用外加电压法或外加电流法求得： 即输入电阻 R in ＝u s /i 或 R in ＝u/ i s方法是：在端口处加一电压源u s （或电流源i s ）, 再求比值u s /i 或u/ i s ，该比值即是一端口无源网络的输入电阻。

u = Us – iRs1 方向：Us与Is “非关联”
3、几点说明
1）变换方法总结
电压源 数值：
电流源
电流源 电压源
电压源的 短路电流
电流源的 开路电压
方向：电压源与电流源方向“非关联”
2）等效变换是对外电路而言的；
Is =Us /Rs1 内阻相等
Us =Is Rs1 内阻相等
3）理想电压源和理想电流源之间不能做等效变换， 因为前者RS=0，后者RS=；
Rs
1）电路模型：理想电压源Us与电阻Rs的串联。 Us
2）伏安关系： u = Us - iRs
对外电路：电压u和电流i参考方向关联。 Us
2、实际电流源模型 1）电路模型：
理想电流源Is和电导Gs(电阻Rs)的并联
2）伏安关系： u = Us - iRs
Us
对外电路：电压u和电流i参考方向关联。
等效变换关系：
Is =Us /Rs1 Rs1 = Rs
方向：Us与Is “非关联”
2、已知电流源模型，求电压源模型 等效条件：保持端口伏安关系相同。
Is
Rs
Rs1
i = Us/Rs1 – u/Rs1Us
电流源 的内阻
电流源的 开路电压
i = Is - u/Rs Us =Is Rs1
等效变换关系： Rs1 = Rs
习题2-6： 求i、US。
四、三个电阻的星形、三角形连接及等效变换
1、电阻的星形、三角形连接
(a) 星形连接（T形、Y形） (b) 三角形连接（形、形）
等效变换：
2、从星形连接变换为三角形连接
R1
R3
R2
R31 R12 R23
变换式：

三. 电阻星形联接、三角形联接旳等效互换 由三角形联接求等效星形联接旳公式
比较（1）式和（4）式，可得：
R1
R12
R31 R12 R23 R31
R2
R12
R23 R12 R23
R31
R3
R12
R23 R31 R23 R31
R12
1
i1
R1
2
R2
i2
R31
R3
R23
i3
3
若 R12＝R23＝R31＝R ，则 R1＝R2＝R3＝RT ， 且 RT＝ (1/3) R 。
在分析含受控源旳电路时，也可用以上多 种等效变换措施化简电路。
但要注意：变换过程中不能让控制变量 消失。
例： 求图示二端 电路旳开路 电压Uab。
解：原电路
4Ω
2Ω
a
2A
+
5Ω
U1
-
2U1 b
4Ω
2Ω
+-
4U1
a
2A
+
5Ω
U1
-
b
Uab 4U1 2 (4 5) U1 2 5 10
Uab 4 10 18 22 (V )
第二章 电阻电路旳等效变换
❖ 2.1 等效二端网络 ❖ 2.2 电压源及电流源串、并联电路旳等效变换 ❖ 2.3 实际电源旳两种模型及其等效变换 ❖ 2.4 电阻星形连接与三角形连接旳等效变换 ❖ 2.5 例题
2.1 等效二端网络
电阻电路
仅由电源和线性电阻构成旳 电路
分析措施
（1）欧姆定律和基尔霍夫定律 是分析电阻电路旳根据；
2.1.2 单口网络端口伏安关系(VAR)旳求取
将单口网络从电路中分离出来，标好其端 口电流、电压旳参照方向；

03
02
01
等效变换的目的
等效变换的基本原则
电压和电流保持不变
在等效变换过程中，电路中的电压和电流值应保持不变。
元件参数相同
等效变换后的元件参数应与原电路中的元件参数相同。
功率平衡
等效变换后的电路应满足功率平衡条件，即电源提供的功率等于负载消耗的功率。
02
电阻的串并联等效变换
总结词
当多个电阻以串联方式连接时，总电阻值等于各电阻值之和。
详细描述
在并联电阻的等效变换中，总电阻倒数1/R_eq等于各个并联电阻倒数1/R1、1/R2、...、1/Rn之和。这种等效变换在电路分析中非常有用，因为它可以帮助我们简化电路模型。
01
02
03
04
电阻并联的等效变换
串并联电阻的等效变换
总结词：串并联电阻的等效变换是电路分析中的重要概念，它涉及到将复杂的串并联电路简化为易于分析的形式。
等效变换方法：对于非线性电阻电路，可以采用分段线性化方法，将非线性电阻的伏安特性曲线分段近似为直线，然后进行等效变换。
05
等效变换在电路分析中的应用
在计算电流和电压中的应用
总结词：简化计算
详细描述：通过等效变换，可以将复杂的电阻电路简化为简单的电路，从而更容易计算电流和电压。
总结词：提高精度
总结词：扩展应用范围
电阻串联的等效变换
总结词
当多个电阻以并联方式连接时，总电阻值倒数等于各电阻值倒数之和。
详细描述
在电路中，如果多个电阻以并联方式连接，则总电阻的倒数等于各电阻倒数之和。这是因为多个电阻并联时，它们共享相同的电压，因此总电流等于各支路电流之和。
总结词
并联电阻的等效变换可以通过公式1/R_eq = 1/R1 + 1/R2 + ... + 1/Rn表示。

电阻电路的等效变换等效变换的概念电路一般等效变换概念电路中的某一部分用另一种结构与元件参数的电路替代后，变换部件以外的电路参数不受影响一端口网络等效两个二端电路，端口具有相同的电压、电流关系电源的等效变换电压源的串并联及等效变换电流源的串并联及等效变换实际电源模型及等效变换电阻元件的等效变换电阻的串联串联分压：Uk=Rk*i=Rk*U/Req;功率：P=i^2Req电阻的并联分流：i=U/Rk；功率：P=U^2/Req;电阻的Y-▲联结的等效变换电桥平衡条件：R2*R4=R1*R3等效条件：u12▲ =u12Yu23▲=u23Yu31▲ =u31Yi1▲ =i1Yi2 ▲ =i2Yi3▲=i3Y▲结：用电压表示电流i1▲=u12▲/R12 –u31▲/R31i2▲=u23▲/R23 –u12▲/R12i3▲=u31▲/R31 –u23▲/R23Y结：用电流表示电压u12Y=R1i1Y– R2i2Yu23Y=R2i2Y – R3i3Yu31Y=R3i3Y – R1i1Y输入电阻一端口无源网络输入电阻的定义对于一个不含独立源的一端口电压，不论内部如何复杂，其端口电压和端电流成正比，定义这个比值为一端口电路的输入电阻Rin=U/i一端口无源网络输入电阻的求法电阻的串并联简化法电阻的Y-▲等效变换法外加电压源或电流法一端口含源（不含受控源）网络输入电阻的求法外加电压源或电流源法电源置零法含受控源一端口无源网络输入电阻的求法外加电压源法外加电流源法。

+
u
_
各电阻顺序连接，流过同一电流 （判断电路是否为串联的依据）
2）等效电阻
R1
Rk
_
_
i
+ u1
+ uk
+
u
由KVL和VAR得：
Rn
_
+ un
_
等效
Req
i
+u
_
u R1i Rki Rni (R1 Rk Rn )i Reqi
n
等效电阻： Req R1 Rk Rn Rk Rk k 1
电阻元件的串、并联对偶记忆
电阻元件
串联
并联
等效变换 分压/分流 公式
功率比
i相同
u相同
Req R1 R2 Rn Geq G1 G2 ... Gn
uk
Rk Req
u
ik
Gk Geq
i
pk1 Rk1 pk 2 Rk 2
pk1 Gk1 pk 2 Gk 2
三、电阻的混联
电路中有电阻的串联，又有电阻的并联，这种连接方式称电阻的串并 联(混联)。
如果一个电路（网络）向外引出一对端钮，这 对端钮可以作为测量用，也可以用来与外部的电源 或其他电路连接用。这类具有一对端钮的电路称为 一端口电路（网络）或二端电路（网络）。
i
+
N
u
i
N0-无源二端网络 Ns-含源二端网络
2.等效二端电路（网络）
N1 i
+
u
i
-
i
+
N2
u
i
若两个二端网络N1和N2与同一个外部相连，当 相接端钮处的电压、电流关系完全相同时，称N1和 N2互为等效的二端网络。

电阻电路的等效变换电阻电路的等效变换是指将一个电阻电路转化为另一个等效的电阻电路，使得两个电路在电学性质上完全相同。

等效变换在电路分析和设计中起着重要的作用，能够简化电路分析过程，提高计算效率。

一、串联电阻的等效变换串联电阻是指多个电阻按顺序连接在一起，电流依次通过每个电阻。

当电路中有多个串联电阻时，可以通过等效变换将其转化为一个等效电阻。

假设有两个串联电阻R1和R2，其等效电阻为Req。

根据欧姆定律可知，串联电阻中的电流相同。

根据电阻的定义可知，电阻与电流和电压之间存在线性关系，即R = U / I。

因此，R1和R2的电阻值可以表示为R1 = U / I1，R2 = U / I2。

在串联电路中，电流I1通过R1，电流I2通过R2，由于串联电路中电流只有一个路径，所以I1 = I2。

将上述两个等式相等，可得到R1 / I1 = R2 / I2，即R1 / R2 = I1 / I2。

由此可推导出串联电阻的等效电阻为Req = R1 + R2。

二、并联电阻的等效变换并联电阻是指多个电阻同时连接在一起，电流分别通过每个电阻。

当电路中有多个并联电阻时，可以通过等效变换将其转化为一个等效电阻。

假设有两个并联电阻R1和R2，其等效电阻为Req。

根据欧姆定律可知，电压在并联电路中相同。

根据电阻的定义可知，电阻与电流和电压之间存在线性关系，即R = U / I。

因此，R1和R2的电阻值可以表示为R1 = U1 / I，R2 = U2 / I。

在并联电路中，电压U1作用在R1上，电压U2作用在R2上，由于并联电路中电压相同，所以U1 = U2。

将上述两个等式相等，可得到R1 / U1 = R2 / U2，即R1 / R2 = U1 / U2。

由此可推导出并联电阻的等效电阻为1 / Req = 1 / R1 + 1 / R2。

三、星型-三角形转换星型电阻网络和三角形电阻网络是常见的电阻网络拓扑结构。

在电路分析中，有时需要将星型电阻网络转换为三角形电阻网络，或将三角形电阻网络转换为星型电阻网络，以便于进行电路分析。

i
R1
+
u
R2
-
VAR:
i + u VAR：
R=R1+R2
注意：当电路中的某一部分用其等效电路替代后，未被替代部分的电压电流均 应保持不变，即“对外等效”。
§2-1 引言
三、等效法
1、等效法：将复杂电路进行等效化简，从而求出各i. u, p的一种分析方法
2、本章内容
电阻的等效变换 电源的等效变换
第二章 电阻电路的等效变换法
R4
Rg
R2
R3
若R1 R3=R2 R4
R1
R4
则电桥平衡
或者
R2
R3
R1
R4
x
R2
R3
第二章 电阻电路的等效变换法
§2-3 Y—△等效变换
一、电阻的Y、△联接 1、为什么需Y—△变换 2、Y形联接
Байду номын сангаас
§2-3 Y—△等效变换
3、△形联接 a
4、举例： 上图：R1.R2.R3 R3.R4.R5——△ R1.R3.R4 R2.R3.R5——Y
+
i
+
US -
U
R0 -
i
+
US R0
R0
U
-
§2-5 两种实际电源的等效变换
2、实际电流源——实际电压源
iS R0
+
i
iSR0 -
R0
3、说明： 注意极性 等效对外电路等效，内部不等效 举例说明其应用 受控源也可以同样等效（但不能将受控变掉）
§2-5 两种实际电源的等效变换
+
U1
-
R0

方法2：加流看压法
原理图：
R in
+
u
-
i 列u、iS为变量的方程
S
u
⇒ Rin = iS
练习1：求端口的最简等效形式
R i1
i
+
βi1
_uS
Rin
判断：是无源网络吗？ 最简形式是什么？
由KCL（设流入为正）： i + i1 − βi1 = 0
由VCR：i1
=
−
uS R
得：
R in
=
uS i
=R
1− β
王馨梅
第二章 电阻电路的等效变换
“电阻电路”：由电阻、独立源、受控源组成 (不含L或C) 等效变换的目的：为了化简电路！
课件符号： ★ 重要 * 大纲之外的知识扩展
§§22--11、、§§22--22 等等效效概概念念
2Ω 1Ω 2Ω
i
+
u
i
+
2Ω
u
-
-
N1
N2
★概念：两个网络的端口伏安特性曲线完全相同，则 称这两个网络对外等效。
但等效电导好求：
n
∑ G eq =
Gk
k =1
i k = G k u = G k × ( R eq ⋅ i ) ⇒
并联分流公式： i k
=
Gk G eq
i
并联电导越大 则分流越大
思考：电阻除了串并联关系之外，还有其它连接方式吗？
三、Δ⎯Y之间的等效变换
引例：
A
B
A
B
A
B
R1
R2
R3
1
R12
2
R31

将三个串联的电阻等效为一个电阻，其电阻为
R R2 R1 R3 4 2 6 12
由图(b)电路可求得电阻RL的电流和电压分别为：
i uS 15V 1A R RL 12 3
u RLi 3 1A 3V
例2－3电路如图2－7(a)所示。已知iS1=10A, iS2=5A, iS3=1A, G1=1S, G2=2S和G3=3S，求电流i1和i3。
u2

R3i1

(R2

R3
)i2

对电阻三角形联接的三端网络，外加两个电流源i1 和i2，将电流源与电阻的并联单口等效变换为一个
电压源与电阻的串联单口，得到图(b)电路，由此得
到
i12

R31i1 R23i2 R12 R23 R31
uu12

R31i1 R31i12 R31 (i1 i12 ) R23i12 R23i2 R23 (i2 i12 )
例2－2 图(a)所示电路。已知uS1=10V, uS2=20V, uS3=5V, R1=2, R2=4, R3=6和RL=3。求电阻RL的电流和电压。
解:为求电阻RL的电压和电流，可将三个串联的电压 源等效为一个电压源，其电压为
uS uS2 uS1 uS3 20V 10V 5V 15V
R3

R12
R23 R31 R23
R31
(2 13)
由此 解得
R2

R12
R12 R23 R23

R31

(2 14)
R2

R3

R23 (R12

R31 )

电阻电路的等效变换n§2-1 引言n§2-2 电路的等效变换n§2-3 电阻的串联和并联n§2-4 电阻的Y形连接和△形连接的等效变换n§2-5 电压源、电流源的串联和并联n§2-6 实际电源的两种模型及其等效变换n§2-7 输入电阻§2-1 引言几个基本概念1、时不变线性电路（简称线性电路）：由时不变线性无源元件、线性受控源和独立电源组成的电路。

2、线性电阻性电路（简称电阻电路）：构成电路的无源元件均为线性电阻。

3、直流电路：当电路中的独立电源都是直流电源时,这类电路简称直流电路。

电路的“等效概念”n上页电路图，图（a）中端子1-2以右的电路被图（b）Req替代后，1-2以左部分电路的任何电压和电流都将维持与原电路相同。

这就是电路的“等效概念”。

n用等效电路的方法求解电路时，电压和电流保持不变的部分仅限于等效电路以外，这就是“对外等效”的概念。

n“对外等效”也就是对外部特性等效。

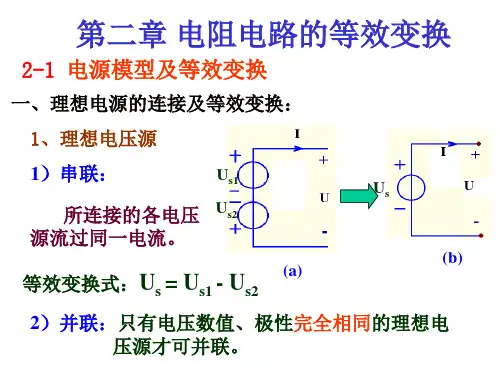
应用KVL，有:应用公式：i i `图2-11(a)为n个电压源的串联，可以用一个电压源等效替图2-12(a)为n个电流源的并联，可以用一个电流源等§2-5电压源、电流源的串联和并联注意n只有电压相等极性一致的电压源才允许并联，否则违背了KVL，其等效电路为其中任一电压源，但是这个组合向外部提供的电流在各个电压源之间是如何分配的无法确定。

n只有电流相等且方向一致的电流源才允许串联，否则违背了KCL，其等效电路为其中任一电流源，但是这个组合向外部提供的总电压在各个电流源之间是如何分配的无法确定。

§2-6图2-13（a）所示为一实际直流电源，例如一个电池；图§2-6图2-14(a)所示为电压源和电阻的串联电路，在端子1-1`§2-6实际电源的两种模型及等效变换i s=Gu s ，则u = u s–R i，i = i s n如果令G=1 / R，–G u两方程将完全相同，也就是在端子1-1`处的u和i 的关系将完全相同.式子G=1 / R，i s=Gu s 就是这两种组合彼此对外等效必须满足的条件（注意u s 和i s 的参考方向，i s 的参考方向由u s 的负极指向正极）.n这种等效变换仅保持端子1-1`外部电路的电压、电流和功率相同（即只是对外部等效），对内部并无等效可言。

§2-3 电阻的串联和并联
一. 电阻串联
Req R1 R2 Rn Rk
def
n
k,
Req Rk
k 1
Rk u k Rk i u Req
二. 电阻并联
Geq G1 G2 Gn Gk
k , Geq Gk ,
ik
def
n
第2章
电阻电路的等效变换
主要内容
1.电路等效变换的概念； 2.电阻的串联和并联; 3.电阻的Y- 等效变换; 4.电压源、电流源的串联和并联； 5.电源的等效变换; 6. 输入电阻。
§2-1 引言
线性电阻电路: 线性电阻 + 线性受控源 + 独立电源
时不变线性电路: 时不变线性无源元件 + 线性受控源 + 独立电源
说明：
① 与电压源 uS 并联的任何一条支路(iS ,R 和一般支路）均 可仅用 uS 替代；
② 与电流源 iS 串联的任何一条支路(uS ,R 和一般支路）均 可仅用 iS 替代；
③ 电压源串联电阻可与电流源并联电阻相互等效
§2-6
实际电源的两种模型及其等效变换
一. 实际电源的伏安特性
二. 实际电源的两种电路模型
例2-2：求下图所示电桥电路中电流 I .
解：利用等效变换公式可得最后等效电路如右上图，则
10 3 . 5 70 I A 3.5 // 5.5 0.25 3.5 5.5 43
利用等效变换求总电阻 （例2-2 PP38）。
§2-5
电压源、电流源的串联和并联
一. 电压源串联 当 n 个电压源串联时，可用一个电压源等效替代
Req 1 , Rk 1 Geq Gk

u31
i2

R1 R2

R1 R2 R3

R3 R1
u23

R1 R2

R3 R2 R3

R3 R1
u12
i3

R1 R2

R2 R2 R3

R3 R1
u31

R1 R2

R1 R2 R3

R3 R1
u23
18
对于电路
i12

u12 R12
i23

u23 R23
i1'
i31
Rsh 1k
14
当K与2相接时分流电阻为R2+R3 ，可测10mA的电流
Ig

I2
( R2

R2 R3 R3 ) (R1

Rg )

I2
R2 R3 Rsh Rg
10A 10m A R2 R3
Ig
RgIg
111.11 1000
R2+R3 =11 .11
R3
R2 R1
R1i1=R2i2 且 R4i4=R3i3
i1=i4 i2=i3
i1 R1 c
R4 i4
a
Ig
b
R2
R3
i2
d +
i3
则： R1 R2 或 R4 R3
根据平衡电桥的特点:
R1R3=R2R4
uS 电桥平衡条件
Ig =0，可将c、d间开路； ucd =0（等电位），可将c、d短路，最后计算的结果相同。
i3'
21
2）形等效为Y形，有：
R1

u U
GsU
工作点
I Is i
电阻电路 的等效变换
3、电源的等效变换 实际电压源、实际电流源两种模型可以进行等效变换， 所谓的等效是指端口的电压、电流在转换过程中保持不变。
+ i + i is Gs i =is – Gsu + u _
us _
Rs
u _ u=us – Rsi us u i Rs Rs
Us RsI I 工作点
us _ Rs
U u=us– Rsi Rs: 电源内阻，一般很小。
i
电阻电路 的等效变换
2、实际电流源 一个实际电流源，可用一个电流为 is 的理想电流源 和一个内电导 Gs 并联的模型来表征其特性。当它向外电 路供给电流时，并不是全部流出，其中一部分将在内部 流动，随着端电压的增加，输出电流减小。 i is Gs i=is – Gsu Gs: 电源内电导，一般很小。 + u _ is=Is时，其外特性曲线如下：
R º 30 30
R º
40 30 R 30 3 2
电阻电路 的等效变换
例 4. + 12V _
I1
I2 R
I3 R
I4 2R + U4 _
+ + 2R U 2 2R _1 2R U _
求： I1、 I4、 U4 解： 可用并联分流或串联分压解题
I 4 - 1 I 3 - 1 I 2 - 1 I 1 - 1 12 - 3 2 4 8 8 R 2R
(b)总电压等于各串联电阻的电压之和（KVL）。
电阻电路 的等效变换
2.等效电阻 Req R1
i + KVL + u1 _

R3 u12 R2 u31 i1 = R1 R2 + R2 R3 + R3 R1 R1 R2 + R2 R3 + R3 R R1 u23 R3 u12 i2 = R1 R2 + R2 R3 + R3 R1 R1 R2 + R2 R3 + R3 R R2 u31 R1 u23 i3 = R1 R2 + R2 R3 + R3 R1 R1 R2 + R2 R3 + R3 R
i
R1
u1
R2
u
u2
R1 u1 = u R1 + R 2
R2 u2 = u R1 + R2
分压公式
二、电阻并联
i
1
u
1. 电路特点 电路特点:
1
'
i1 G1
i2
G2
in Gn
(a) 各电阻两端分别接在一起，两端为同一电压 (KVL)； 各电阻两端分别接在一起， ； (b) 总电流等于流过各并联电阻的电流之和 (KCL)。 。
根据理想化的伏安特性， 根据理想化的伏安特性，可以用电压源和电阻串联组 合或电流源和电导的并联组合作为实际电源的电路组合 。
i
1
u
us
Ri
us
u
R
0
1
'
u = us Ri
us / R
i
i
is
G
1
u
is / G
u
0
1
'
Gu
i = is Gu
is
i
u = us Ri
i = is Gu
如果令： 如果令：