哈工大水力学课件第5章 量纲分析与相似原理(彩色)

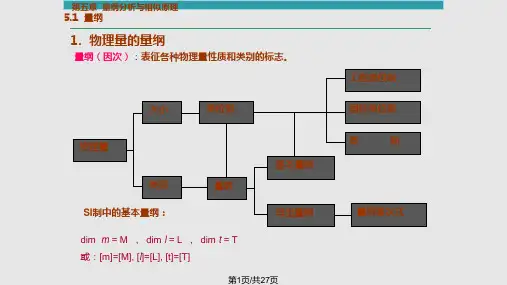
第章量纲分析和相似原理第5章§5.1 量纲分析的意义和量纲和谐原理 §5.2 量纲分析法53§5.3 相似理论基础§模型实验5.4一、量纲的概念单位（Unit）：量度各种物理量数值大小的标准量，：量度各种物理量数值大小的标准量称单位。

如长度单位为m或cm等。

——“量”的表征。

量纲（Dimension）：撇开单位的大小，表征物理量的Di i撇开单位的大小表征物理量的性质和类别。

如长度量纲为[L]。

——“质”的表征。

基本量纲（Fundamental Dimension）：具有独立性的，不能由其他量纲推导出来的量纲叫做基本量纲。

不可压缩流体运动中般取质量M、基本量纲。

不可压缩流体运动中一般取质量M、长度L、时间T、即[M-L-T]为基本量纲体系。

量纲导出量纲（Derived Dimension）:是指由基本量纲导出的量纲。

［］［ρ］[]A= L2=ML-3[ F]= MLT-2量纲公式:不可压缩流体中，某一物理量q 的量纲[q ］都可用3个基本量纲的指数乘积形式表示αβγ几何学量纲[]q M L T =几何学量纲：α= 0，β≠0，γ=0运动学量纲0β分运动学量纲：α= 0，β≠0，γ≠0类动力学量纲：α≠0，β≠0，γ≠0二、无量纲量三、量纲和谐原理量纲和谐原理的重要性：a、一个方程在量纲上应是和谐的，所以可用来检验物理方程或经验公式的正确性和完整性。

b、根据量纲和谐原理可用来确定公式中物理量的指数。

c、可用来建立物理方程式的结构形式。

为科学地组织实验过程、整理实验成果提供理论指导。

织实验过程整理实验成果提供一、瑞利法（Rayleigh ）瑞利法是量纲和谐原理的直接应用瑞利法是量纲和谐原理的直接应用。

具体分析步骤如下：1、确定与所研究的物理现象有关的n 个物理量；2、写出各物理量之间的指数乘积的形式，如：2a b p =LL 11i n q Kq q q −3、根据量纲和谐原理，即等式两端的量纲应该相同，确定物理量的指数a ，b ，……p ，代入指数方程式即得各物理量之间的关系式。

[][][][]121a b p i n q q q q −=LL应用范围：一般情况下，要求相关物理量个数n 不超个待求量纲指数不超过个过4个，待求量纲指数不超过3个。

【例4-1】求水泵输出功率的表达式【例41】求水泵输出功率的表达式(1)()确定关系式找出同水泵输出功率N 相关的物理量，包括单位体积水的重量γ=ρg 、流量Q 、扬程H ，即(,,,)0f N Q H γ=(2)写出指数乘积关系式a b cN K Q H γ=(3)写出量纲式[][][][]a b cN Q H γ=(4)以基本量纲（M 、L 、T ）表示各物理量量纲232231()()()a b cML T ML T L T L −−−−=1(5)根据量纲和谐原理求量纲指数:1:223M aL a b c==−++:32T a b−=−−111得1,1,a b c ===(6)整理方程式N K QHγ=二、布金汉（Buckingham ）定理（π定理）若某一物理过程包含n 个物理量，即)0123(,,n f q q q q =LL 个基本量（量纲独立不能相互导出的物理量）其中有m 个基本量（量纲独立，不能相互导出的物理量）则该物理过程可由n－m n 个物理量构成的n m 个无量纲项所表达的关系式来描述，即12(,)0n m F πππ−=LLπ定理的解题步骤：应用范围：对相关物理量个数n 没有限制，应用更为普遍选择基本变量的原则：即若各物理量中基本量纲更为普遍。

1）基本变量与基本量纲相对应。

即若各物理量中基本量纲（M ，L ，T ）出现三个，那么基本变量也选三个；倘若基本量纲只出现两个，则基本变量只须选择两个。

）选择基本变量时应选择重要的变量换句话说不要2）选择基本变量时，应选择重要的变量。

换句话说，不要选择次要的变量作为基本变量，否则次要的变量在大多数项中出现，往往使问题复杂化，甚至要重新求解。

）不能有任何两个基本变量的量纲是完全样的换言之3）不能有任何两个基本变量的量纲是完全一样的，换言之，例用布金汉定理确定圆管流动中边壁切应力的表达式知τ0与液体的密度ρ，液体的动力沾滞系数μ，圆管直径D，液体的动力沾滞系数圆管直径管壁材料的粗糙度管中紊流，单位管长沿程水头损失进行量纲分析，则有一、流动相似原型(Prototype)：天然流体和实际建筑物称为原型。

模型(Model)：通常把原型（工程实物）按一定比例关系缩小（或放大）的代表物，称为模型。

表物称为模型水力学模型试验的目的：利用模型流动来模拟和研究原型流动问题。

关键问题：使模型流动和原型流动保持流动相似。

流动相似若两个流动的对应点的同名物理量如流动相似：若两个流动的对应点上的同名物理量（如速度、压强及各种作用力等）具有各自的固定比例关系，则这两个流动就是相似的。

定关则两个动就似模型和原型保证流动相似，应满足：•几何相似•运动相似•动力相似•初始条件和边界条件相似1. 几何相似3.动力相似（初始条件和界条件相似4.初始条件和边界条件相似指两个流动相应边界性质相同，如原边界条件相似指两个流动相应边界性质相同如原型中有固体壁面，模型中相应部分也是固体壁面；原型中的自由液面模型相应部分也是自由液面原型中的自由液面，模型相应部分也是自由液面。

对于非恒定流动，还要满足初始条件相似；而对于恒定流动，无需初始条件相似。

流动相似的进步解释流动相似的进一步解释：边界条件和初始条件相似以及几何相似是流动相似的前提与依据；的前提与依据是决定流体运动相似的主导因素；动力相似是决定流体动相似的导因素；运动相似是几何相似和动力相似的最终表现，是流动相似的目标；动相似的目标凡流动相似的原型与模型流动，必然同时满足几何凡动相似与模动然同时满几何相似、动力相似和运动相似。

du T=2.弗劳德（重力）准则3. 欧拉（压力）准则§5.3 相似理论基础思考题：为什么每个相似准则都要表征惯性力？作用在流体上的力除惯性力是企图维持流体原来运动状态的力外，其他力都是企图改变运动状态的力。

如果把作用在流体上的各力组成一个力多边形的话，那么惯性力则是这个力多边形的合力即牛顿定律流动的r 则是这个力多边形的合力，即牛顿定律，流动的变化就是惯性力与其他上述各种力相互作用的结果。

因此a m F r =∑各种力之间的比例关系应以惯性力为一方来相互比较。

建立与原型相似的小尺度模型进行实验研究，并以模建似尺度模行实研究并模型实验的结果预测原型将会发生的流动现象及规律。

一、模型律的选择原型与模型流动雷诺数相等的这个相似条件，称为雷诺模型律。

原型与模型流动弗劳德数相等的这个相似条件称为为了使模型和原型流动完全相似除要几何相似外原型与模型流动弗劳德数相等的这个相似条件，称为弗劳德模型律。

为了使模型和原型流动完全相似，除要几何相似外，各独立的相似准则应同时满足。

但实际上要同时满足各准则很困难甚至是不可能的足各准则很困难，甚至是不可能的。

模型实验想做到与原型完全流动相似是困难的，一般只能达到近似相似，就是保证对流动起主要作用的力相似，这就是模型律的选择问题，这就是模型律的选择问题。

实际模型试验中，根据流动的特点，抓住主要矛盾。

在几何相似的基础上，只满足雷诺模型律，或者只满足弗劳德模型律，或者两者都不满足（处于自模区，只需满足几何相似），即可近似认为流动相似，在主要方面满足试验要求。

在主要方面满足试验要求二、模型设计步骤：1通常是先根据实验场地模型制做和量测条件定1、通常是先根据实验场地，模型制做和量测条件定出长度比尺；再以选定的比尺缩小原型的几何尺寸得出模型区的几何边界l λ2根据对流动受力情况分析满足对流动寸，得出模型区的几何边界；2、根据对流动受力情况分析，满足对流动起主要作用的力相似，抓住主要矛盾选择模型律；3、最后按所选用的相似准则，确定流速比尺及模型的流量。

v λ例长度比进时，测得波浪阻力为原型中船舶航行速度；（1. 量纲分析的意义和量纲和谐原理1）量纲的概念2）基本量纲与导出量纲[]q M L T αβγ=3）无量纲量[]1q =4）量纲和谐原理：凡是正确反映客观规律的物理方程，其各项的量纲都必须是一致的，即只有方程两边量纲相同，方程才能成立。

2. 量纲分析法1）瑞利法2）π定理法3. 相似理论基础1）流动相似：几何相似、运动相似、动力相似、边界条件动相似几何相似动相似动力相似界条件和初始条件相似。

）相似准则4. 模型实验1）模型律的选择2）模型设计定出长度比尺；再以选定的比尺缩小原型的几何尺寸，得模型的何边l λ根据对流动受力情况分析，满足对流动起主要作用的力相似，出模型区的几何边界；抓住主要矛盾选择模型律；最后按所选用的相似准则，确定流速比尺及模型的流量。

v λ。