菱形的存在性(教师版)
- 格式:pdf
- 大小:8.16 MB
- 文档页数:28
一道菱形存在性问题的解析教学设计
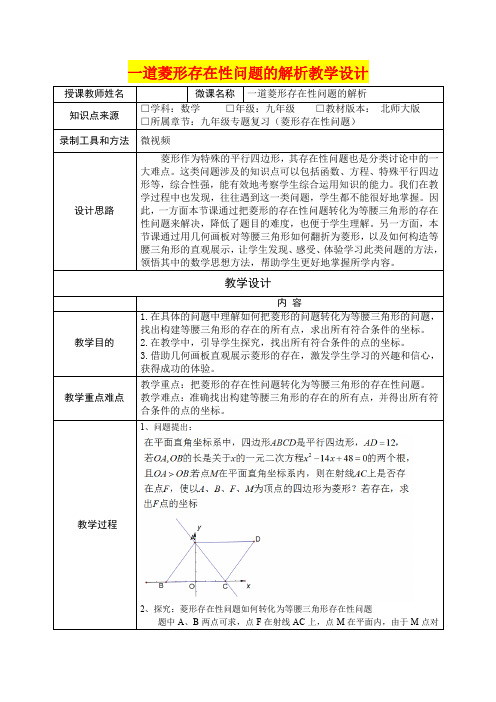
1、问题提出:
2、探究:菱形存在性问题如何转化为等腰三角形存在性问题
题中A、B两点可求,点F在射线AC上,点M在平面内,由于M点对
构成菱形没有影响,我们只需要研究F点的情况。
也就是找到F点,使△ABF 为等腰三角形,我们就可以通过等腰三角形沿底边翻折得到菱形。
我们就把找以A、B、F、M为顶点的菱形转化为找以A、B、F为顶点的等腰三角形,也就是只需要找出F点坐标即可。
从而把菱形存在性问题转化为等腰三角形存在性问题来解决。
3、分析求解:分情况讨论,求解等腰三角形第三个点的坐标
进一步分析,由于分别沿等腰三角形的两条腰以及底边翻折,得到以下三种不同的菱形。
因此,只需要讨论等腰三角形ABF的存在性。
分三种情况:(1)以B为顶角顶点,即AB=BF;(2)以A为顶角顶点,即AB=AF;(3)以F为顶角顶点,即AF=BF。
再通过几何画板对这三种情况进行展示和解析。
情况一:
情况二:
情况三:
4、反思总结:
总结符合条件的菱形的三种情况,以及对应F点的坐标。
引导学生总结菱形存在性问题的关键就是转化为等腰三角形的问题。

千里之行,始于足下。
202X年中考数学复习存在性问题系列菱形的存在性问题专题探究202X年中考数学复习存在性问题系列——菱形的存在性问题专题探究一、引言菱形是中学数学中常见的一种图形,是四边形的一种特殊状况。
在几何学中,我们通常将具有相等对角线长度的四边形称为菱形。
然而,在菱形的定义和性质方面,中同学往往存在一些常见的错误和迷思。
本文将通过对菱形的存在性问题进行专题探究,分析常见的错误观念,并提出正确的解决方法,以挂念同学正确生疏菱形的存在性问题。
二、错误观念分析1. 菱形必需是正方形这是一个常见的错误观念。
很多同学认为只有四边形的四个内角都是直角时,才能称之为菱形。
然而,这种理解是不正确的。
事实上,菱形只需要满足对角线相等即可,对角线之间的夹角并没有限制。
2. 任意平行四边形都可以称为菱形这也是一个常见的错误观念。
很多同学认为只要四边形的对边平行且对角线相等,就可以称其为菱形。
然而,这种理解也是不正确的。
事实上,菱形是一种特殊的四边形,除了要满足对角线相等外,还必需满足两对相邻边相等。
三、正确解决方法第1页/共3页锲而不舍,金石可镂。
1. 基本定义菱形的定义是:两对对角线相等的四边形称为菱形。
这是菱形存在的基本条件,也是区分菱形和其他四边形的关键特征。
2. 避开混淆同学在解决菱形存在性问题时,需要避开将菱形和其他外形混淆。
例如,正方形和菱形是两个不同的概念,虽然正方形也是一种菱形,但并不是全部的菱形都必需是正方形。
3. 留意推断在推断一个四边形是否为菱形时,可以通过测量四条边的长度和对角线的长度来进行推断。
假如对角线的长度相等,并且两对相邻边的长度也相等,那么这个四边形就是一个菱形。
否则,它就不是菱形。
四、进一步探究1. 菱形的性质菱形具有一些特殊的性质,同学可以通过进一步的探究来加深对菱形的生疏。
例如,菱形的内角和为360度,对角线的交点可以将菱形划分为四个全等的三角形等等。
2. 利用菱形解决问题千里之行,始于足下。


菱形的性质与判定教案一、菱形的定义菱形是指四边形的四条边都相等的图形,同时对角线互相垂直且长度相等。
二、菱形的性质1.菱形的对角线互相垂直且长度相等。
2.菱形的对边平行。
3.菱形的内角和为360度,每个内角为90度。
4.菱形的内切圆和外接圆均存在。
5.菱形的对角线平分内角。
6.菱形的对角线交点是菱形的中心,也是内切圆和外接圆的圆心。
7.菱形的面积等于对角线长度之积的一半。
三、菱形的判定方法1.判定四边形的四条边相等。
2.判定四边形的对角线互相垂直。
3.判定四边形的对角线长度相等。
4.判定四边形的对边平行。
5.判定四边形的内角和为360度,每个内角为90度。
四、菱形的应用1.菱形常用于制作菱形形状的物品,如菱形钻石、菱形标志等。
2.菱形也常用于数学中的几何问题,如计算菱形的面积、判定是否为菱形等。
3.菱形还可以用于设计中,如在平面设计中使用菱形来表达某种意义或情感。
五、菱形的例题1.已知菱形ABCD,AC=8cm,BD=6cm,求菱形ABCD的面积。
解:菱形ABCD的面积等于对角线长度之积的一半,即S=AC×BD÷2=8×6÷2=24cm²。
2.已知四边形EFGH,EF=GH=5cm,EG=FH=12cm,判断四边形EFGH是否为菱形。
解:由于EF=GH,EG=FH,且对角线EG和FH互相垂直,因此四边形EFGH是菱形。
六、总结菱形是一种四边形,其四条边相等,对角线互相垂直且长度相等。
菱形具有对边平行、内角和为360度、对角线平分内角等性质。
判定菱形的方法包括判定四边形的四条边相等、对角线互相垂直、对角线长度相等、对边平行、内角和为360度等。
菱形常用于制作物品、数学中的几何问题、设计中的表达等方面。


菱形的证明方式菱形是一种平面图形,它具有四条边相等、四个角都是直角等特征。
下面将介绍几种证明菱形的方法。
方法一:利用菱形的判定定理证明菱形的判定定理指出,如果一个平面图形中,所有边长都相等,并且所有角都是直角,那么该图形就是菱形。
可以利用这个定理来证明菱形的存在性。
假设存在一个菱形,则四边长度相等,且四个角都是直角。
根据菱形的判定定理,这个平面图形中所有边长都相等,因此可以画出一个边长为 1 的正方形。
由于正方形的四个角都是 90 度,因此它可以作为菱形的菱心,证明菱形的存在性。
方法二:利用菱形的性质证明菱形具有许多特殊性质,例如四边相等、对角线相等、对角线交点是菱形中心等。
可以利用这些性质来证明菱形的存在性。
假设存在一个菱形,则四边长度相等,我们可以用任意一边的长度作为菱形的边长,画出一个正方形。
根据菱形的性质,菱形的对角线相等,且对角线把菱形分成两个面积相等的部分。
由于正方形的面积等于边长的平方,因此菱形的面积等于正方形的面积乘以边长,即菱形的面积为正方形的面积乘以边长。
由于菱形的边长为任意长,因此菱形的面积可以是任意大,因此不存在菱形。
方法三:利用菱形的构造方法证明菱形的构造方法是指,用正多边形构造出菱形,然后通过旋转、平移等操作,将正多边形构造出的菱形转化为标准菱形。
可以利用菱形的构造方法来证明菱形的存在性。
假设存在一个菱形,则四边长度相等。
我们可以用正六边形构造出菱形,然后将正六边形通过旋转、平移等操作,转化为标准菱形。
由于正六边形的边长为 1,因此可以通过计算得到,标准菱形的边长为√2。
由于四边长度相等,因此标准菱形的面积为 1,因此不存在菱形。
综上所述,以上介绍了三种证明菱形的方法,包括利用菱形的判定定理证明、利用菱形的性质证明和利用菱形的构造方法证明。
最新一次函数--菱形存在性问题菱形存在性问题(Diamond Problem)是指在多继承结构中,如果两个父类具有相同的方法名,并且子类没有重写该方法,就会导致菱形存在性问题。
问题描述考虑以下多继承结构:A/ \B C\ /D假设父类 A、B 和 C 中都有一个名为 `foo` 的方法。
如果子类D 没有重写 `foo` 方法,那么当 D 调用 `foo` 方法时,会发生菱形存在性问题。
问题的原因和影响菱形存在性问题的产生是由于多继承的特性所致。
当子类继承多个父类时,如果这些父类中的某些方法名相同且未被子类重写,那么就无法确定该方法应该调用哪个父类中的实现。
这可能导致代码出现意料之外的行为或错误。
解决方案为了解决菱形存在性问题,可以采用以下策略:1. 使用虚拟继承:虚拟继承是一种特殊的继承方式,在多继承中使用它可以解决菱形存在性问题。
通过虚拟继承,可以确保父类的实例在子类中只有一个实例,从而避免了重复继承导致的问题。
2. 明确指定调用的父类方法:如果虚拟继承不适用或无法使用,可以通过在调用父类方法时明确指定调用的父类来解决问题。
如`B::foo()` 表示调用父类 B 的 `foo` 方法。
这些解决方案可以根据具体情况选择使用,以避免菱形存在性问题的发生。
结论菱形存在性问题是多继承中的一个常见问题,但可以通过适当的解决方案来避免或解决。
在设计和实现多继承结构时,需要注意方法名的冲突,并采取相应的措施来确保代码的正确性和可维护性。
文章字数:XXX(根据具体内容进行修改)。