第3章 点、直线、平面的投影 复习思考题答案

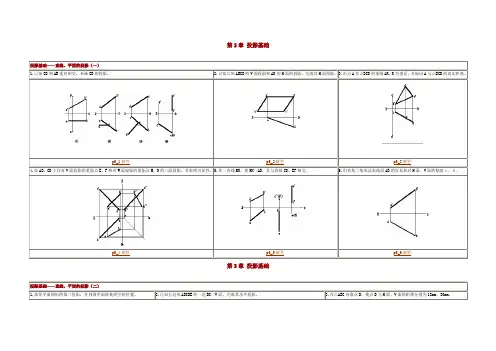
第3章直线与平面、平面与平面的相对位置复习思考题答案3.1.直线与平面的相对位置有哪几种？其中有哪些对作图有利的特殊状态？答：直线与平面的相对位置有平行和相交，相交的特殊情况是垂直。

对作图有利的特殊状态是指直线、平面的投影具有积聚性。

3.2.平面与平面的相对位置有哪几种？如何进行判断？答：平面与平面的相对位置有平行和相交，相交的特殊情况是垂直。

同一平面内的两相交直线，若分别平行另一平面内的两相交直线，则两平面平行。

两平面不平行就相交。

如果一平面内包含另一个平面的垂直直线，那么这两个平面垂直。

3.3.直线与平面相交，交点有何特性？如何判断可见性？答：直线与平面相交，交点有是平面与直线的共有点。

可见性判断直接根据直线与平面边界的重影点的可见性来判断。

3.4.平面与平面的交线如何求得？可见性判断有哪些方式？答：平面与平面的相交有两种情况：一是有平面投影具有积聚性，此时积聚投影的共有部分就是交线的该面投影，再利用交线是两个平面的共有线求得其它投影：二是两个一般位置平面相交，此时交线就用线面相交法或三面共点法求作。

具体见章节3.2.43.5.空间几何元素的距离如何确定？特殊位置的平面在确定距离的题目中起何作用？答：距离是平行的空间元素之间的间距，空间几何元素的距离都会经过这三步：作垂线，求交点，求垂线段的实长。

特殊位置的平面是指具有积聚性，或直线平行于投影面。

当平面积聚时，其垂线与平面所垂直的投影面平行，其垂线在此投影面的投影长度就是真实距离；当两直线与投影面平行时，可以直接使用直角投影定理找到公垂线，此时只需要用直角三角形法求公垂线实长即可得到此种情况下平行二直线的距离。

所以，作图关键在于找到平面的积聚投影，或直线的显实投影。

第三章 点、直线及平面投影
§3－1 点的投影 §3－2 直线的投影 §3－3 平面的投影
点线面的投影规律
通过上一节的学习及画图实践，可以体会到 画一个物体的三视图，实质上是画出组成物体的 各个面的投影，而各个面是由棱线围成的，各棱 线是由两个端点决定的。
因此，为了迅速而正确地画出物体的视图， 还需研究构成物体的基本几何元素点、线、面的 投影。
Y
H
向下翻
●a
O
W
ay
Y
a ●
X ax
a●
点的投影规律
Z az
a
●
Z
V a
●
az
O
Y
ay
A
X ax
●
●a
O
W
ay
Y
a●
ay
H
Y
① aa⊥OX轴
aa⊥OZ轴
连影垂轴
② aax= aaz= y = A 到 V 面的距离 aax= aay= z = A 到 H 面的距离 aay= aaz= x = A 到 W 面的距离
Z
X
V a′ A
a″ W
a b
a
Z a
b
O
YW
b′
B b″
b
判断方法：
YH
x
ab
H
Y
x 坐标大的在左 y 坐标大的在前
z 坐标大的在上
例2.已知B点在A下10，A后5，A左10 mm处，求B点的三投影。 作图步骤：（1）根据B的相对位置求 其V.H面的投影 b’,b;
（2）根据点的投影规律,求其第三投影 b”。
§3－1 点的投影
一、点在一个投影面上的投影
P

画法几何点、直线与平面的 投影
点的投影
例题3-1：根据投影图判断点在空间的位置
b'
V
B
X
a'
b
c' c
O
C
a A
二、点的三面投影
1.三面投影体系
2.点的三面投影 Z
（X，Z） a '
a"（Y，Z）
X
X
ax
（X，Y）a
Z
O
Y
aYw
点的三面投影规律：
YW
a 'a " OZ
aYH
aYHO = aYwO
b'
a' X
b1'
O
b
a
30º
二、直线上的点
点在直线上，点的投影必在直线的同名投影上
定比性：AC：CB=a 'c ':c 'b '=ac:cb=a"c" :c "b "
d' b' c' e' a'
X
O
d'
D
a
e
cd
d
b
例题5 例题3-8: 在直线AB上找一点K,AK:KB=3:2。
b'
3
2
k' a'
c b
a d
c'
a'
b'
d' c
a
b
d
例题3-17：求两直线AB与CD之间的距离。
公垂线
b'
c'
e'
f'
a'

侧垂线（垂直于W面，同时平行于H、V面的直线）
V
Z a b ab B W O a Ha X O YW a b Z a(b)
A X
b YH
b
Y
侧面投影积聚为一点；水平投 影及正面投影平行于OX轴，且 反映实长。
投影面垂直线的投影特性
投影面垂直线的投影特性可概括如下：
（1）直线在它所垂直的投影面上的投影积聚成一点；
c'
c
例3：已知C点在直线AB上，求作C点的水平投影。
1、用等比分割作图 2、利用侧面投影作图
a" c" b"
c c
例4：根据投影图判断C点是否在直线AB上。
求解一般位置直线的实长及倾角
根据一般位置直线的投影求解其实长及 倾角是画法几何综合习题中的常遇见的基本 问题之一，也是工程实际中经常需要解决的 问题。而用直角三角形法求解实长及倾角最 为简便、快捷。
一、直线投影的形成
连两 影 一 况 即个 ， 直 下 可点 只 线 仍 由 。的 需 ， 为 于 投作故直直 影出要线线 ，已获，的 再知得且投 将直直两影 它线线点一 们上的决般 相的投定情
V
a'
b'
B
X
A
O b a H
直线的分类
投影面垂直线 特殊位置直线
直 线
投影面平行线 一般位置直线
二、特殊位置直线
水平投影到OX轴的距 离等于侧面投影到OZ轴 的距离（宽相等）。
a
ay YH
可得出点的投影特性如下： （1）点的投影的连线垂直于相应的投影轴。
（2）点的投影到投影轴的距离，反映该点到相应的投影面的距离。
【例3-1】 已知点A的水平投影a和正面投影a′，求其 侧面投影a″ 解: 作图步骤如下

03
添加标题
侧平线
侧垂线
水平线
A
正垂线
B
一般位置直线
3-2.2、作 出下列直线 的三面投影
01.
答案
02.
正平线AB,在点B在点A之右上方， γ=30°，AB=20mm。
b）正垂线CD，点D在点C之 右后，CD=18mm。
答案
答案
3-2.3、在直线AB上取一点K， 使AK：KB=3：2；
答案
在直线CD上取一点E使CE： ED=2：1.
3-2.4、在直线EF上取一点p，使P点与H面、 V面距离之比为3：2
答案
3-3.1、判别直线AB和CD的相对位 置（平行、相交、交叉）
交叉
相交
交叉
相交
2.作一正平线MN,使其与已知直线AB、CD和EF均相交。
答案
3.作一直线L,与直线AB、GH相交,并与直线MN平行。
5.在直线AB、CD上作对正面投影的重影点E、F和对侧面 投影的重影点M、N的三面投影，并表明可见性。
2.已知平面图形的两个投影，求作第三个投影，并判断平面的空间位置。
三角形是
面
1
5
平面图形是
面
4
2 水平 3 侧垂
第一章节
3-4.3、已知矩形ABCD⊥H面， β=45°，完成其水平投影。
1.作出△ABC平面内三边形DEM的水平投影。
2.完成平面图形ABCDEF的正面投影。
3.已知平面ABCD的边BC//H面，完成其正面投影。
4.判断点K是否在平面上。
3-5.5、求平面上点K与点 N的另一投影。
单击此处添加小标题
三角形是
面
单面图形是
面
单击此处添加小标题

2-22 已知CD为水平线,完成平面ABCD的正面投影。
2-23 完成平面图形ABCDEFGH的三投影并回答 下面的问题。
平面ABCDEFGH是 一般位置 面。 直线EF是 水平 线。 直线FG是 侧平 线。
2-24 判断下列各图中的直线与平面是否平行（将“是” 或"否"填于括弧中）。
⑴
⑵
( 是)
2-1 求各点的未知投影。
2-2 已知点B距点A15；点C与点A是对V面的重影点；点D
在点A的正下方15。求各点的三面投影。
2-3 已知点A(25,15,20)；点B距W、V、H面分别为20、10、15； 点C在点A之左10、之前15、之上12；点D在点A之上5、与H、
V面等距、距W面12。求作各点的三面投影并填写下表。
2-8 判断两直线的相对位置（平行、相交、交叉、垂直相交、 垂直交叉）并将答案填写在下面的括号内。
2-9 由点A作直线AB与直线CD相交并使交点 距H面12。
2-10 求直线AB、CD的交点K。
2-11 过点C作直线CD与已知直线AB平行。
2-12 作与已知直线AB、CD平行且相距为15的直线MN，并使MN的 实长为20，点M距W面30，点N在点M之右（任求一解）。
2-13 作正平线EF距V面15,并与直线AB、CD相交 （点E、F分别在直线AB、CD上）。
2-14 作直线EF平行于OX轴,并与直线AB、CD相交 （点E、F分别在直线AB、CD上）。
2-15 过点C作一直线与直线AB和OX轴都相交。
2-16 作一直线MN，使其与已知直线CD、EF相交，同时 与已知直线AB平行(点M、N分别在直线CD、EF上)。
2-4 已知直线AB的实长为15，求作其三面投影。

3．两直线交叉
交叉两直线各组同面投影不会都平行，特殊情况下可能有一两组 平行；其各组同面投影交点的连线与相应的投影轴不垂直，即不符合 点的投影规律。
重影点 反之，如果两直线的投影既不符合平行两直线的投影特性，也不 符合相交两直线的投影特性，则该两直线空间为交叉两直线。
4．两直线垂直
一般情况下，在投影图中不能确定空间两直线是否垂直， 但当直线处于特殊位置时可以直接从投影图中判断：
三、正投影的基本性质
1. 实形性
2．积聚性
∟
三、正投影的基本性质
3.类似性
4．平行性
三、正投影的基本性质
5．定比性
6．从属性
3-2 三视图的形成及其投影关系
一、 三视图的形成
1. 三投影面体系的建立
物体的一个投影不能确定空间物体的形状。
怎吗办？
建立三面投影体系
2．三视图的形成
主视图
左 视图
[例3-4] 已知点A(15,10,12)，求作点A的三面投影图。
作图步骤如下：
1.自原点O沿OX轴向左量取x=15,得点 ax 2.过ax作OX轴的垂线，在垂线上自ax向下量取y=10,得点A的水平投影a 向上量取z=12,得点A的正面投影a
3.根据点的投影规律，可由点的两个投影作出第三投影 a 。
★ 我们只讨论直线与平面中至少有一个处于特殊位置的情况。
[例3-11] 求一般位置直线MN与铅垂面ABC的交点 分析： 作图：
判可见性：
[例3-12] 求铅垂线MN与一般位置平面△ABC的交点 分析： 作图：
判可见性：
⒉ 两平面相交
两平面相交其交线为直线，交线是两平面的共 有线，同时交线上的点都是两平面的共有点。

12、在标注锥度时，锥度符号的方向应与图中锥度的方向（ ） （a）一致； （b）垂直； （c）倾斜； （d）任意。
13、绘制连接圆弧图时，应确定（ ）。 （a）切点的位置； （b）连接圆弧的圆心； （c）先定圆心再定切点； （d）连接圆弧的大小。
2021/7/17
5
《机械制图》复习思考题
——第一章 制图的基本知识（4）
（c）尺寸界线、尺寸线和尺寸数字； （d）尺寸线、箭头和尺寸数字。
2021/7/17
4
《机械制图》复习思考题
——第一章 制图的基本知识（3）
10、图形上标注的尺寸数字表示（ ）。 （a）画图的尺寸； （b）机件的实际尺寸； （c）随比例变化的尺寸； （d）图线的长度尺寸。
11、标注角度的尺寸时，角度数字应（ ）注写。 （a）水平方向书写； （b）竖直方向书写； （c）与线性尺寸数字的方向一致； （d）向心方向书写。
8、能用直角三角形法求一般位置直线实长的一组已知条件是（ ）。
（a）ab，b'； （b） ab ,a' b' ； （c）ab，a‘；
（d）a'b'，a。
9、在下列两直线的V、H面投影中，不能直接判断其平行的是（ ）。
（a）两水平线； （b）两正平线；
（c）两侧平线； （d）两侧垂线。
10、在V、H面投影中，相交的两直线是（ ）。
（b）必须用点画线画出；
（c）当体小于一半时才不画出； （d）当体小于等于一半时均不画出。
11、轴线垂直于H面的圆柱的正向最外轮廓素线在左视图中的投影位置在（ ）。
（a）左边铅垂线上；
（b）右边铅垂线上；
（c）轴线上；
（d）上下水平线上。
12、圆锥的4条最外轮廓素线在投影为圆的视图中的投影位置（ ）。

5.作一直线MN，使MN//AB，且与直线CD、EF相交。
6.用直角三角形法求线段AB的实长和对H面、V面的倾角α、β。
p6_4解答
p6_5解答
p6_6解答
第3章投影基础
投影基础——直线、平面的投影（二）
1.求作平面图形的第三投影，并判别平面所处的空间位置。
2.已知五边形ABCDE的一边BC//V面，完成其水平投影。
p7_4解答
p7_5解答
p7_6解答
第3章投影基础
投影基础——平面的投影（一）
1.判别下列直线与平面、平面与平面是否平行？
2.求作直线CD与△LMN的交点，并表明可见性。
3.求作铅垂线AB与△CDE的交点，并表明可见性。
p8_1解答
p8_2解答
p8_3解答
6.根据下列诸投影图中直线与平面或两平面的相对位置，分别在下面的括号内填写“平行”、“垂直”或“倾斜”。
p10_4解答
p10_5解答
p10_6解答
p9_1解答
p9_2解答
p9_3解答
4.过点K作直线平行于△ABC和△EFG。
5.过点K作平面平行于直线EF，且垂直于正方形ABCD。
6.补画以AB为底的等腰△ABC的水平投影。
p9_4解答
p9_5解答
p9_6解答
第3章投影基础
投影基础——平面的投影（三）
1.已知直线DE的端点E比D高，DE=50mm，用换面法求作d'e'。
2.用换面法求作点K到直线AB的距离及其投影。
3.已知正方形的边AB，点C在B的前上方，正方形对V面的倾角β=45°，补画正方形的两面投影。
p10_1解答
p10_2解答
p10_3解答

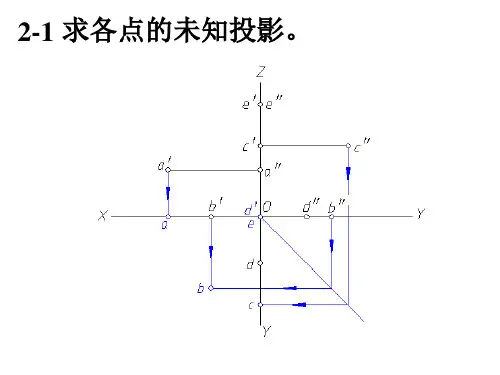
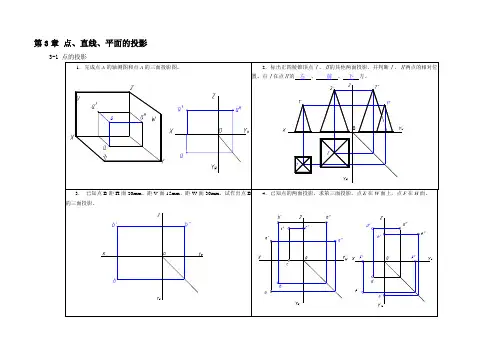
一、点、直线、平面的投影1.1 点的投影∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙第24～24页习题1.2 直线的投影∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙第25～27页习题1.3 平面的投影∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙第28～29页习题1.4 直线与平面、平面与平面相对关系∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙第30～32页习题1234题号：题号：56789101112131415题号：161718192021题号：2223242526272829303132333435363738391.5 换面法∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙第33～35页习题1.6 旋转法∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙第36～36页习题1.7 投影变换综合题∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙第37～37页习题点、直线、平面的投影题号：404142434445464748495051题号：525354555657题号：58596061621. 已知A、B、C三点的直观图，画出它们的投影图，并将各点的坐标值填入表中。

2. 已知A、B、C各点对投影面的距离，画出它们的三面投影图和直观图。

3. 已知点Ａ的坐标（40，15，0），画出其三面投影并作出点Ｂ和点Ｃ的三面投影。

（a）点B ——在点Ａ右面20mm，前面15mm，上面20mm；（b）点C ——在点Ａ左面10mm，后面15mm，上面15mm。

3．完成带缺口的正四棱锥的H面和W面投影。
2．在△ABC内作距V面为15mm的正平线。
2．过点C作直线CD与直线AB相交，交点距V面15mm。
3．作直线MN平行AB，且与CD、EF相交。
4．判断两直线的相对位置。
5．用字母标出交叉两直线重影点的投影。
3-7平面的投影(找出平面Ⅰ的另两视图，判断空间位置)
1．
2．
3．
4．
3-8平面的投影
1．已知点K属于△ABC平面，完成△ABC的正面投影。
第3章点、直线、平面的投影
3-1点的投影
1．完成点A的轴测图和点A的三面投影图。
2．标出正四棱锥顶点Ⅰ、Ⅱ的其他两面投影，并判断Ⅰ、Ⅱ两点的相对位置。点Ⅰ在点Ⅱ的左、前、下方。
3．已知点B距H面20mm、距V面15mm、距W面30mm，试作出点B的三面投影。
4．已知点的两面投影，求第三面投影。点E在W面上，点F在H面。
3-3直线的投影
1．已知点A在点B的左方15mm、下方10mm、前方10mm，求A、B两点的三面投影。
2．在正五棱台的主视图、左视图上标出A、B两点的投影，并比较两点的相对位置。点B在点A的右、前、上方。
3．已知A、B两点在W面的投影重影，完成A、B两点的三面投影。
4．已知正三棱锥的俯视图，其锥顶S距H面25mm，又知锥底位于H面上，试补画主、左视图。
3-4直线的投影
1．作直线AB的H面投影，并标出它与V、W面的倾角β和γ。
2．求作正平线CD的三面投影，已知CD长25mm，与H面倾角为30°。
3．求侧垂线EF的三面投影，已知EF长30mm，距V面15mm，距H面20mm，端点E距W面40mm。
4．已知点M在直线CD上，并与H、V面的距离相等，完成点M的投影。

title工程制图基础(华东交通大学) 中国大学mooc答案100分最新版content第1章绪论点、直线、平面的投影第1章测试1、点到投影面的距离，下列说法正确的是（）答案: 点到H面的距离等于点的Z坐标，点到V面的距离等于点的Y坐标，点到W面的距离等于点的X 坐标2、判别A、B、C三点的相对位置，正确的答案是（）答案: A点在B点的左、前、下方，C点在B点的右、前、下方3、用正投影得到的投影具有以下基本性质（ )答案: 真实性、类似性、积聚性、平行性、从属性、等比性4、下列关于直线位置的说法，正确的答案是（ )答案: AB是水平线，CD是侧垂线，EF是一般位置直线5、下列说法正确的是（）答案: 投影法有中心投影法、平行投影法二种，其中平行投影法又分斜投影法、正投影法二种6、求直线AB对投影面V、H的倾角，正确的是（）答案: (C)7、判别交叉两直线AB、CD上重影点的可见性，正确的是（）答案: (D)8、如图所示，判别直线的相对位置，正确的是( )答案: AB与CD交叉，CD与EF交叉9、空间前后方位用哪个坐标轴表示？答案: 坐标轴Y10、以下哪种投影图的度量性最好？答案: 多面正投影图11、以下哪种投影图的直观性最好？答案: 透视投影图12、完成五边形平面ABCDE的水平投影，正确的是（ )答案: (C)13、已知正方形ABCD的一个顶点D在V面上，完成正方形ABCD的两投影，求作过程正确的是（）答案: (B)14、空间A点的正面投影记为：( )答案: a¢15、图中a¢ax =Aa表示的含义为：( )答案: 空间A点的正面投影到X轴的距离等于A点到水平投影面的距离16、空间A点的侧面投影记为：( )答案: a²17、关于点的三面投影规律描述正确的是：( )答案: a¢a⊥OX轴、a¢a²⊥OZ轴、aax=a²az，简称“长对正、高平齐、宽相等”18、关于直线AB描述正确的是：( )答案: AB是水平线19、关于直线AB描述正确的是：( )答案: AB是正垂线20、在一般位置平面P内取一直线AB，已知ab∥OX轴，直线AB是：( )答案: 正平线21、关于C点的位置描述正确的是：答案: C点不在直线AB上22、关于直线AB与CD位置关系描述正确的是：答案: AB与CD交叉23、关于直线AB与CD位置关系描述最正确的是：( )答案: AB与CD交叉垂直24、一条正平线与一条一般位置直线在空间垂直，投影图中互相垂直的是：( )答案: 正面投影25、求A点到BC直线的距离实长时，能从投影图中直接量取距离实长的已知条件是：答案: BC直线为铅垂线26、下图中?号所表示的角为：答案: 直线AB对水平投影面的倾角27、直角三角形法求一般位置直线AB对正投影面的倾角β，下图中正确的是：答案: （C）28、用直角三角形法求一般位置直线AB对H面的倾角α，描述正确的是：答案: 直角三角形的一条直角边是直线的水平投影，另一条直角边是直线两端点的Z坐标差29、下图中关于△ABC叙述正确的是：答案: △ABC是铅垂面30、下图中关于△ABC叙述正确的是：答案: △ABC是正平面31、平面的正面投影积聚为一条直线并与OX轴平行，该平面是：答案: 水平面32、下图中关于AN与与△ABC的关系叙述正确的是：答案: AN是△ABC面上的水平线33、工程中常用的投影图有（）答案: 多面正投影图;标高投影图;轴测图投影;透视投影图34、下面的投影图中哪些采用了正投影法（）答案: 正等轴测投影图;标高投影图;三视图35、采用第一角投影法的国家有（）答案: 俄罗斯;中国36、投影面W可反映空间哪几个方位（）答案: 上下;前后37、下图中关于K点与△ABC的关系叙述正确的是K在△ABC平面上答案: 正确38、空间A点的正面投影记为：( )答案: a¢39、空间A点的侧面投影记为：( )答案: a²40、下图中关于△ABC叙述正确的是：答案: △ABC是正平面41、下图中关于△ABC叙述正确的是：答案: △ABC是铅垂面42、下图中关于△ABC叙述正确的是：答案: △ABC是正平面43、平面的正面投影积聚为一条直线并与OX轴平行，该平面是：答案: 侧平面44、下图中关于AN与与△ABC的关系叙述正确的是：答案: AN是△ABC面上的水平线45、下图中关于K点与△ABC的关系叙述正确的是K在△ABC平面上答案: 正确作业第1章绪论点、直线、平面的投影第1章作业1、评分规则:2、评分规则:3、评分规则:作业第2章直线、平面相对位置第2章作业1、评分规则:2、评分规则:3、评分规则:4、评分规则:第2章直线、平面相对位置第2章测试1、求两平面的交线，并判断可见性。

3.斜二测图的轴向伸缩系数是D
（A）p=q=r=1（B）p=q=r=0.82（C）p=r=1,q=0.5（D）p=q=1,r=0.5
4.形体只在正平面上有圆、半圆、圆角时，作图简单的轴测图是B
（A）正等测（B）斜二测（C）正二测（D）前三者一样
5.平行于正面的正方形，对角线平行于X轴、Z轴，它的正等测图是D
12.平面的正面投影积聚为一条直线并与OX轴平行，该平面是B
（A）正平面（B）水平面（C）正垂面（D）铅垂面
13.能取到正垂线的平面是C
（A）铅垂面（B）一般位置平面（C）正垂面（D）侧垂面
14.在一般位置平面P内取一直线AB,已知ab∥OX轴,直线AB是B
（A）水平线（B）正平线（C）侧平线（D）侧垂线
（A）6个（B）5个（C）4个（D）3个
16.如图所示，两体相交所产生相贯线的特殊点有C
（A）8个（B）4个（C）5个（D）6个
第五单元轴测图（单项选择题）
1.获得正轴测图的投影方法是B
（A）中心投影法（B）正投影法（C）斜投影法（D）平行投影法
2.斜二测图的轴间角是C
（A）都是90（B）都是1200（C）900,1350,1350（D）900,900,1350
2.空间点A只有y坐标为零时，空间位置在D
（A）原点处（B）W面上（C）OX轴上（D）V面上
3.空间点A在点B的正左方，这两个点为B
（A）H面的重影点（B）W面的重影点（C）V面和W面的重影点（D）V面的重影点
4.下列几组点中，哪一组是W面上的重影点，并且A点为可见A
（A）A(5，10，8)、B(10，10，8)（B）A(10，10，8)、B(10，10，5)（C）A(10，30，-5)、B(8，30，-5)（D）A(10，30，8)、B(10，20，8)

Z
(a') b'
a"
X
O
a
b
YH
Z
b"
b' a' a" b"
Yw X
O
Yw
a
b
YH
Z
e'
e"
f'
X
O
e
f
YH
Z
n' n"
f"
m'
m"
Yw X
O
Yw
n
m
YH
工程图学习题集 第 3 章
·17 ·
3.2.6 参照立体图，试在投影图上标出AB，AC，AD各直线的投影，并在图的下方说明是何种位置 直线。（投影图上用小写字母表示）
平面B是侧垂面
平面B是一般位置平面
工程图学习题集 第 3 章
·20 ·
3.3.3 直线ＭＮ在已知平面内，画出它的另一投影。
1 . a
b
2 . e
n
m
n
m
f
3.3.4 E、F两点及其直线在ABCD平面内，画出 它们的另一投影。
b
c
e
1
2 f
b
c
e f
d
X
c
oX
d e
a
oX
a 2 1
d
d
X
d
o
a
21
d
·22 ·
3.3.12 已知平面图形为铅垂面，且Z与V面成30°，试补
画全下列平面的各投影。
f'
a'
a" f"

k′（l′）的可见性时，由于K、L两点的水平投影k比l的y坐标值大，所以当从前往后看时，点K可见，点L不可见，由此可判定AB在CD的前方。同理，从上往下看时，点M可见，点N不可见，可判定CD在AB的上方。
（a） （b）
课后练习
复习思考题；3-2题、3-3题
第3讲
课题
面的投影
课型
理 论
教学
目的
掌握各种位置平面的投影规律
（一）投影面平行线
平行于一个投影面且同时倾斜于另外两个投影面的直线称为投影面平行线。平行于V面的称为正平线；平行于H面的称为水平线；平行于W面的称为侧平线。
直线与投影面所夹的角称为直线对投影面的倾角。α、β、γ分别表示直线对H面、V面、W面的倾角。
投影面平行线的立体图、投影图及投影特征
名称
正平线（//V）
2．一直线和直线外一点
3．相交两直线4．平行两来自线5．任意平面图形，如三角形、四边形、圆形等
在投影图上判定两直线是否平行；若两直线处于一般位置时，则只需观察两直线中的任何两组同面投影是否互相平行即可判定；但当两平行直线平行于某一投影面时，则需观察两直线在所平行的那个投影面上的投影是否互相平行才能确定。如图所示，两直线AB、CD均为侧平线，虽然ab∥cd、a′b′∥c′d′，但不能断言两直线平行，还必需求作两直线的侧面投影进行判定，由于图中所示两直线的侧面投影a″b″与c″d″相交，所以可判定直线AB、CD不平行。
（3）面投影e′f′∥OX轴，侧面投
影e″f″∥OYW，且都小于实长。
（1）侧面投影i//j//反映实长。
（2）侧面投影i″j″与OZ轴和OYW轴的夹角β和α分别为EF对V面和H面的倾角。
（3）正面投影i′j′∥OZ轴，水平投影ij∥OYH，且都小于实长。

A面是 B面是 C面是 D面是
面 面 面 面
3-18 过点 A 作矩形ABCD, 短边 AB=20mm 且垂直于V 面, 长边BC=40mm,α
=30°,求作矩形ABCD的投影（求一解）。
分析： (1)由已知条件可知短 边AB为正垂线，故可 作出短边AB的两面投 影。 (2)因矩形ABCD的短 边AB为正垂线，故可 知矩形ABCD为正垂面 ，又因矩形的相邻两 边互相垂直故可知AD 和BC为正平线。
(1)
3-16 求平面的第三投影，并判别其相对投影面的位置，在投影图 上反映倾角实形处用 α 、β 、γ 表示之。
(2)
3-16 求平面的第三投影，并判别其相对投影面的位置，在投影图 上反映倾角实形处用 α 、β 、γ 表示之。
(3)
3-17 在投影图上用字符标出平面A、B、C、D的三面投影,并判别其 相对投影面的位置。
3-12 判断两直线的相对位置。
(1) (2) (3) (4)
3-13 作图判别直线AB与CD在空间的相对位置。
3-14 过点A作直线AB,使平行于直线DE；作直线AC使与直线DE相交，其交 点距V面为15mm。
3-15 求作水平线MN 与交叉三直线AB、CD、EF均相交。
3-16 求平面的第三投影，并判别其相对投影面的位置，在投影图上反映 倾角实形处用 α 、β 、γ 表示之。
3-11 已知直线 AB 的投影，试定出属于 AB 线段的点 C 的投影，使 AC:CB=3:2，并求AB和点C的W投影。
作图步骤： 1.任作一直线a′N, 量取五单位长，使 a′M:MN=3:2。 2.连接Nb′,作 Mc′//Nb′,得c′。 3.按点的投影规律 作出c和c′点，以 及投影a"b"。

已知
a'
作图
d'
c'
直线的投影——应用题
3.求直线AB与CD的距离.
c m b' c' a' a' X d' a c(d ) O
X
土木工程制图 习题集
b'
d'
c'
a' X d' a
a
距离
O
c(d )
b
姓名
土木工程制图 习题集
a' a' O b
a'
△
b'
c' b' O
b' X
X
X
b
b
△
c
a a a
20
姓名
C0
直线的投影
直线上点
班级
已知
作图
直线的投影——直线上的点
4.在直线AB上求一点C，使点C与H、V面等距。
b' a' X
b
土木工程制图 习题集
Z
b' c' a'
YW
Z
a″ c″ b″
45°
X
b
YW
c
a'
d'
a' m' 20 n'
d'
c' X c a
b' O d
X X
c'
b' O
c a m
n
d
b
4.求作正平线MN与交叉三直线AB、CD、EF相交。
b
4.求作正平线MN与交叉三直线AB、CD、EF相交。