点的平面位置的测设方法
- 格式:doc
- 大小:92.00 KB
- 文档页数:9

建筑物细部点平面位置测设方法
建筑物细部点平面位置测设方法可以采用以下步骤:1. 制定测绘计划:确定测设目标和测量的具体要求,包括测量范围、精度要求等。
2. 确定测量控制点:选择适当位置设置控制点,通常选择建筑物的角点或者突出的特征点作为控制点。
3. 进行控制点测量:利用全站仪、GPS等测量仪器对控制点进行测量,获取其平面坐标。
4. 采用合适的测量方法:根据具体需求选择合适的测量方法,例如直接测量、交会测量、辅助测量等方法。
5. 进行细部点测量:根据测量需求,在控制点附近选择合适的测点进行测量,通常使用全站仪对测点进行定位和测距。
6. 数据处理和分析:将测得的数据进行处理和分析,包括坐标计算、误差分析等。
7. 编制测绘图件:根据测量结果绘制相应的测绘图件,如平面图、剖面图等。
8. 进行质量检查:对测绘图件和测量数据进行质量检查,确保测量结果的准确性和可靠性。
以上是一般的建筑物细部点平面位置测设方法,具体的测设方法还需要根据实际情况进行调整和完善。

平面点位的测设方法
平面点位的测设方法有多种,下面列举几种常用的方法:
1. 直接测量法:通过直接使用测量仪器(如全站仪、经纬仪、平板测距仪等)对目标点位进行测量,获取其坐标数值。
2. 铺设基准线法:先铺设一条已知长度的基准线,然后使用测量仪器对基准线的两个端点进行测量,再通过后续的观测量测出目标点的坐标。
3. 三边测量法:通过测量目标点与两个已知点之间的距离,并结合已知的两个点的坐标,利用三角形的几何关系计算出目标点的坐标。
4. 等高线插值法:通过在已知等高线的交点上测量目标点与交点之间的距离,并结合已知点的等高线高程,利用等距线之间的关系计算出目标点的高程。
5. 视觉测量法:借助光学仪器(如经纬仪、光电测距仪等)对目标点进行观测,通过测量仪器所测得的角度或长度数据计算出目标点的坐标。
需要根据具体的测量要求和场地条件选择合适的测设方法,并结合测量仪器的使用说明进行操作。


二测设的基本工作及方法施工测量的基本任务是正确地将各种建筑物的位胃(平面及高程)在实地标定出来,而距离、角度和高程是构成位置的基本要素因此,在施工测量中,经常需要进行距离、角度和高程测设工作,距离、角度和高程是测设的基本工作,1. 测设已知水平距离在地面上测设已知水平距离是从地面一个已知点开始,沿已知方向,量出给定的实地水平距离,定出这段距离的另一端点:根据测量仪器工具不同,主要有以下两种方法。
1.钢尺测设法(1)一般测设方法:当测设精度要求不高时,可从起始点开始,沿给定的方向和长度,用钢尺量距,定出水平距离的终点。
为了校核,可将钢尺移动l0cm-20 cm.,再测设一次。
若两次测设之差在允许范围内,取它们的平均位置作为终点最后位置:(2)精确测设方法、在实地测设巳知距离与在地面上丈量两点间距离的过程正好相反。
测设精度要求较高时,应先根据给定的水平距离D,结合尺长改正数、温度变化和地面高低改正计算出地面上应测没的距离L其计算公式为:L=D-(∆L d+∆L t+∆L) (1-1)式中:∆L d—尺长改正数∆L t—温度改正数∆L——高差改正数然后根据计算结果,使用检定过的钢尺,用经纬仪定线.沿已知方向用钢尺进行测设。
现举例说明测设过程:如图10-1所示,从A点沿AC方向在倾斜地面上测设B点,使水平距离D=60m,所用钢尺的尺长方程式为:L=30 m十0.003 m+12.5X10-6 ℃-1X 30X(t-20℃)m测设之前,通过概量定出终点,用水准仪测得两点之间的高差为h=+1.200mo测设时温度为t=4℃,测设时拉力与检定钢尺时拉力相同,均为100N。
先求应测设距离L的长度。
根据已知条件,按第4章的公式求出三项改正数:、计算如下:∆L d=D l∆/l0=60 m×0 003 m/30m=十0。
006m∆L t=Da(t-t0)=60m×12.5×10-6℃×(4-20) ℃=-0.012m∆L h=-h2/(2D)=-(1.2)2/(2×60m)=-0。

《建筑工程测量》测设点位的方法点的平面位置测设,是根据已布设好的控制点的坐标和待测设点的坐标,反算出测设数据,即控制点和待测设点之间的水平距离和水平角,再利用上述测设方法标定出设计点位。
本任务要求学生掌握测设点位的常用方法。
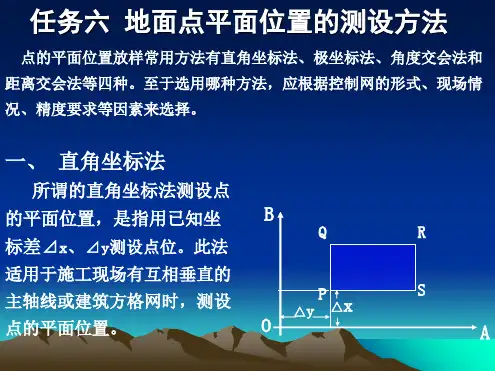
一、直角坐标法直角坐标法是建立在直角坐标原理基础上测设点位的一种方法。
当建筑场地已建立有相互垂直的主轴线或建筑方格网时,一般采用此法。
图8-12直角坐标法测设点位如图8-12所示,A, B, C, D为建筑方格网或建筑基线控制点,1, 2, 3,4点为待测设建筑物轴线的交点,建筑方格网或建筑基线分别平行或垂直待测设建筑物的轴线。
根据控制点的坐标和待测设点的坐标,可以汁算出两者之间的坐标增量。
下面以测设1、2点为例,说明测设方法。
首先,计算出A点与1、2点之间的坐标增量,即81 = “皿力]=力-力测设1、2点平面位置时,在A点安置经纬仪,照准C点,沿此视线方向从A沿C 方向测设水平距离△ yAl定出1'点。
再安置经纬仪于1'点,盘左照准C点(或A点),转90°给出视线方向,沿此方向分别测设出水平距离Mu和Ax⑵定1、2两点。
同样的方法以盘右位置定出,再定出1、2两点,取1、2两点盘左和盘右的中点,即为所求点位置。
采用同样的方法,可以测设3、4点的位置。
检查时,可以在已测设的点上架设经纬仪,检测各个角度是否符合设计要求, 并丈量各条边长。
如果待测设点位的精度要求较高,可以利用精确方法测设水平距离和水平角。
二、极坐标法极坐标法是根据控制点、水平角和水平距离测设点平面位置的方法。
在控制点与测设点间便于使用钢尺量距的情况下,釆用此法较为适宜;而利用测距仪或全站仪测设水平距离,则没有此项限制,且工作效率和精度都较高。
如图8-13所示,4(x知*)、3(x心)为已知控制点,l(xi r yi)> 2(x Zf y2)点为待测设点。
根据已知点坐标和测设点坐标,按坐标反算方法求出测设数据,即:Di_,D2i6i=aAr(XABi^2=ClA2-^AB^测设时,经纬仪安置在A点,后视B点,置度盘为零,按盘左盘右分中法测设水平角队、0S定出1、2点方向,沿此方向测设水平距离2、2则可以在地面标定出设计点位1、2两点。

点平面测设的方法
平面测量的方法包括直接测量和间接测量。
1. 直接测量:
- 杆量法:使用测量杆或测量尺直接测量需要的长度或距离。
- 角量法:使用角度量具如经纬仪或经纬仪等直接测量角度。
- 钢带量法:使用钢带或钢尺直接测量较长距离。
- 钢带测斜法:使用钢带或钢尺测量水平距离和垂直高差,然后计算倾斜角度。
- 剖面仪法:使用剖面仪从平面图上测量长度和高差。
2. 间接测量:
- 三角测量法:根据三角形的几何关系,通过测量两条边和夹角来计算未知长度或角度。
- 相似三角形法:利用相似三角形的比例关系,通过已知长度和长度的比例来计算一些未知长度。
- 特殊测距法:如剖面测距、曲线测距等,根据特定的条件和几何关系测量长度。
- 方位角法:利用方位角的概念和方位角的变化关系在平面上进行测量。
每种测量方法在不同情况下适用,根据具体的测量要求选择合适的方法。
同时,不同方法的精度和适用性也有所差异,需要根据实际需要进行选择。



点的平面位置的测设方法点的平面位置的测设方法有直角坐标法、极坐标法、角度交会法和距离交会法。
至于采用那种方法,应根据控制网的形式、地形情况、现场条件及精度要求等因素确定。
一、直角坐标法直角坐标法是根据直角坐标原理,利用纵横坐标之差,测设点的平面位置。
直角坐标法适用于施工控制网为建筑方格网或建筑基线的形式,且量距方便的建筑施工场地。
1.计算测设数据如上图所示,Ⅰ、Ⅱ、Ⅲ、Ⅳ为建筑施工场地的建筑方格网点,a 、b 、c 、d 为欲测设建筑物的四个角点,根据设计图上各点坐标值,可求出建筑物的长度、宽度及测设数据。
m 00.50m 00.530m 00.580=-=-=a c y y 建筑物的长度 m 00.30m 00.620m 00.650=-=-=a c x x 建筑物的宽度测设a 点的测设数据(Ⅰ点与a 点的纵横坐标之差):m 00.20m 00.600m 00.620=-=-=∆I x x x ax :700.00m x :650.00m x :620.00m x :600.00m y :600.00my :580.00m y :530.00my :500.00ma bcd mnⅠ ⅡⅢⅣ图1 直角坐标法m 00.30m 00.500m 00.530=-=-=∆I y y y a2.点位测设方法(1)在Ⅰ点安置经纬仪,瞄准Ⅳ点,沿视线方向测设距离30.00m ,定出m 点,继续向前测设50.00m ,定出n 点。
(2)在m 点安置经纬仪,瞄准Ⅳ点,按逆时针方向测设90˚角,由m 点沿视线方向测设距离20.00m ,定出a 点,作出标志,再向前测设30.00m ,定出b 点,作出标志。
(3)在n 点安置经纬仪,瞄准Ⅰ点,按顺时针方向测设90˚角,由n 点沿视线方向测设距离20.00m ,定出d 点,作出标志,再向前测设30.00m ,定出c 点,作出标志。
(4)检查建筑物四角是否等于90˚,各边长是否等于设计长度,其误差均应在限差以内。

《普通测量学》习题集参考答案《普通测量学》习题集答案⼀、填空题1、确定点的空间位置需要三个量,即平⾯位置和⾼程。
2、测量⼯作的基本原则是从整体到局部、先控制后碎部、步步有检核。
3、确定地⾯点位的基本要素是⾓度、距离、⾼程。
4、确定地⾯点位外业要观测的三个基本元素是(⾓度)、(距离)、(⾼差)。
5、我国的国家统⼀平⾯坐标系采⽤的是(⾼斯平⾯直⾓)坐标系。
6、国家统⼀划分六度投影带第19带的中央⼦午线是东经( 111度)。
7、地⾯点到⼤地⽔准⾯的铅垂距离称之为该点的绝对⾼程;相对⾼程是指地⾯点到(假定⽔准⾯)的铅垂距离。
8、⽔准测量中,所采⽤的校核⽅法是(计算检核)、(测站检核)、(成果检核);⽽每站校核的⽅法通常采⽤(双⾯尺法)和(变动仪器⾼)法进⾏。
9、在⽔准测量中,、前后视距相等主要是消除(仪器校正后残差)误差和(地球曲率和⼤⽓折光)误差。
10、在⽔准测量中,转点的作⽤是传递⾼程。
11、当闭合或附合⽔准测量的闭合差在允许范围以内时,应将闭合差按测站数或距离成正⽐例的原则,以反符号调整到各测段⾼差上去。
12、附和⽔准路线⾼差闭合差计算公式为()h f h H H =--∑测终始13、⽔准仪后视点⾼程为1001.55m ,后视读数为1.55 m ,⽔准仪的视线⾼为1003.1m 。
14、如果测站⾼差为负值,则后视⽴尺点位置⾼于前视⽴尺点位置。
15、某闭合⽔准路线各测段的⾼差实测值分别为:+2.343m ;-4.003m ;+1.655m ,其⾼差闭合差为(-0.005m )。
16、已知B点⾼程为941.236m ,A点到B点的⾼差为:-1.167m ,则A点的⾼程为(942.403m )。
17、经纬仪对中的⽬的是(把仪器中⼼安置在测站点的铅垂线上)、整平的⽬的是(使仪器竖轴竖直、⽔平度盘⽔平)。
18、⽔平⾓的观测⽅法主要有(测回法)和(⽅向观测法)两种⽅法。
19、经纬仪的安置⼯作包括对中、整平两项内容。
测设点位的四种方法一、背景随着现代科学技术的发展,各种新型测量仪器如雨后春笋般涌现,有效地促进着测量技术的发展。
在工程测量中,点位测量是非常重要的部分。
点位测量是指在大地坐标系或工程坐标系下,对某个点的平面坐标、高程以及角度进行测量的一种方法,也称为基础测量。
在点位测量中,由于地球的曲率和主要的地球自转,许多测量结果都存在一些误差,因此需要使用一些方法来提高测量的精度和准确性。
二、手工测量方法手工测量方法是基础测量最原始的方法之一。
这种方法主要是通过手工的方式来测量点位,使用的仪器主要是经纬仪、水准仪和测角仪。
1.经纬仪经纬仪是一种测量大地方位角度的仪器,主要用于方位角度的测量。
在测量时,经纬仪要放置在点位中心,并且调整好水平。
与方向调节器配合使用,可以得出该点基线方位方向的观测数据。
2.水准仪水准仪是测量高程差的仪器,是测量点位高程的主要仪器之一。
在测量时,需要将水准仪放置在基准点上,测量测站到基准点的高程距离差来得出该点高程。
3.测角仪1.全站仪全站仪是一种功能强大的电子测量仪器,可以测量点位的位置、高程和角度等信息。
在测量时,需要将全站仪放置在点位中心,使用望远镜观测点位及目标,通过测量仪器上的角度读数来得出该点位置的坐标和高程信息。
2.激光测距仪激光测距仪是一种快速测量距离的仪器,可以通过激光指向目标来得到目标与仪器的距离。
在测量时,需要将激光测距仪放置在点位中心,并且调整好指针朝向目标,通过激光测距仪上的显示屏来得到该点与目标的距离信息。
3.GPSGPS是一种用于测量地球真实位置的卫星定位系统,可以获得点位的经度、纬度和高度等信息。
在测量时,需要通过GPS接收器来接收卫星信号,得到该点的坐标信息。
四、无人机测量方法无人机测量是一种依靠无人机进行测量的方法,通过低空飞行的航拍和摄像机拍摄照片来获取点位信息。
在测量时,需要将无人机飞行到点位附近,然后使用相机拍摄该点位的照片。
使用无人机测量的优点是可以快速高效地获取大量点位信息,并且可以通过三维重建技术来得到高精度的测量结果。
测设地面点平面图位置的基本方法测设放样点平面位置的基本方法有:直角坐标法、极坐标法、角度交会法、距离交会法。
一、极坐标法放样极坐标法是在一个控制点上,以已知方向线为后视边,顺时针方向测设一个水平角,在前视边长,从测站点起测设一段设计距离,来确定设计点的平面位置。
例:已知A (Xa ,Ya ),B (Xb ,Yb ),放样P (Xp ,Yp )点。
首先计算放样数据:B A B y -y 1tan x -ABAx θ-= P A p y -y 1tanx -AP A x θ-=Ap D = 如图3.1所示,AB 为已知方向线,P 为设计点,放样时先在极点A 安置经纬仪,后视B 点,顺时针方向测设已知角β;在前视方向线上,从A 点起放样设计距离Ap D ,则终点就是设计点P 的位置。
根据A 、B 、P 点的平面坐标,利用坐标反算公式,可以计算AB 、AP 边的坐标方位角并求出水平角β以及边长Ap D 。
二、直角坐标法放样当施工场地布设有建筑方格网或彼此垂直的轴线时,可以根据已知两条互相垂直的方向线来进行放样。
该法具有计算简单、放样方便等优点。
如图3.2所示,施工现场布设有200m ×200m 的建筑方格网,某厂房4个交点的坐标为已知,现以角点1为例说明放样方法:根据角点1的设计坐标计算出纵横坐标差1x ∆、1y ∆ ;先将经纬仪安置在方格网的角点M 上,正镜,找准另一个角点Q ,沿此方向线从M 点用钢尺测设距离1y ∆,标定终点N ;再将一切移置于N 点,后视,找准M 点,用正倒镜测设直角,在标定的垂线上,从N 点测设距离1x ∆,即可标定1点。
其它角点2、3、4可以用同样方法测设。
最后,应测量1-2、2-3、3-4、4-1边的长度,以检验放样长度与设计长度之差是符合规范要求。
三、角度交会法大中型混泥土拱坝、深水中的桥墩和高层建筑物定位时,由于结构物的尺寸较大,形状 复杂,直接测设距离困难,因此,可采用前方交会法放样,它是工程建设中常用的一种放样方法,现将放样方法及其精度介绍如下。
已知角度的测设测设已知角度时,只给出一个方向,按已知角值,在地面上测定另一方向。
如图4-3,OA 为已知方向,要在O 点测设α角。
为此,在O 点设置经纬仪,以正镜测设α值得B'。
为了消除仪器误差的影响,再以倒镜测设α角得B"。
取B'B"之中得B 1,则∠AOB 1即为所设之角。
图4-3 已知角度放样图 若要精确的测设α角度,则按上法定出∠AOB 1之后,再用经纬仪测出∠AOB 1之角值为α',α'与给定的α值之差为Δα(图4-4)。
为了精确设置α角,过B 1作OB 1的垂线,并在垂线上量取B 1B 得B 点,∠AOB 即为精确测设的α角度。
图4-4 精测已知角示意图B 1B 按下式计算:ρα∆⨯=11OB BB (4-17)式中 ρ=206265",即一个弧度的角,以秒计。
建筑物细部点的平面位置的测设放出一点的平面位置的方法很多,要根据控制网的形式及分布、放线的精度要求及施工现场的条件来选用。
直角坐标法当建筑场地的施工控制网为方格网或轴线网形式时,采用直角坐标法放线最为方便。
如图4-5所示,G1、G2、G3、G4为方格网点,现在要在地面上测出一点A。
为此,沿G2-G3边量取G2A',使G2A'等于A与G2横坐标之差Δx,然后在A'设置经纬仪测设G2-G3边的垂线,在垂线上量取A'A,使A'A等于A与G2纵坐标之差Δy,则A点即为所求。
图4-5 直角坐标放线图从上述可见,用直角坐标法测定一已知点的位置时,只须要按其坐标差数量取距离和测设直角,用加减法计算即可,工作方便,并便于检查,测量精度亦较高。
极坐标法极坐标法适用于测设点靠近控制点,便于量距的地方。
用极坐标法测定一点的平面位置时,系在一个控制点上进行,但该点必须与另一控制点通视。
根据测定点与控制点的坐标,计算出它们之间的夹角(极角β)与距离(极距S),按β与S之值即可将给定的点位定出。
测设点的平面位置和高程实验报告(一)测设点的平面位置和高程实验报告1. 引言在土木工程、测绘工程等领域中,测定点的平面位置和高程是非常重要的任务。
本报告旨在总结与分析进行测设点的平面位置和高程实验的过程、方法和结果。
2. 实验目的•确定测设点在平面上的位置•确定测设点的高程•验证测量结果的准确性和可靠性3. 实验设备和材料•全站仪•支架三脚架•测量棒•基准点4. 实验步骤1.设置全站仪和支架三脚架,确保水平稳定。
2.选择合适的基准点,并将其坐标及高程记录下来。
3.在需要测设的点上设置测量棒,并记录其坐标和高程。
4.利用全站仪进行测量,获取测设点与基准点之间的距离和角度数据。
5.分别计算测设点在水平方向和竖直方向上的平面位置和高程。
5. 实验结果与分析通过实验所获得的测设点的平面位置和高程数据如下:•点1:平面位置(x, y) = (10, 5),高程(z) =•点2:平面位置(x, y) = (15, 12),高程(z) =•点3:平面位置(x, y) = (8, 20),高程(z) =根据实验结果的准确性和可靠性,我们可以得出结论:测设点的平面位置和高程实验具有较高的精度和可信度。
6. 实验总结本次实验成功地完成了测设点的平面位置和高程测量,并且得到了准确可靠的实验结果。
通过实验,我们进一步了解了全站仪的使用方法和测量原理,并提高了实际操作的技能和经验。
7. 实验改进方向为进一步提高测设点平面位置和高程实验的精度和效率,可以考虑以下改进方向: - 使用更精密的测量仪器和设备,如高性能全站仪。
- 进行多组重复测量,以提高数据的可靠性和一致性。
以上为针对测设点的平面位置和高程实验的报告,通过本次实验的结果和总结,我们可以为后续的相关工程提供准确的测量依据和指导。
测设点的平面位置和高程实验报告(续)8. 实验中的注意事项在进行测设点的平面位置和高程实验时,需要注意以下事项: - 确保测设点和基准点之间没有遮挡物和干扰物。
点平面测设的方法点平面测设是指在地面或工程施工中,通过对点的位置坐标进行测量和定位的方法。
它被广泛应用于土木工程、建筑工程、地理调查、环境监测等领域。
下面将详细介绍一些点平面测设的方法。
1. 全站仪法全站仪法是一种高精度、高效率的测量方法,它通过全站仪测量器具,能够同时测量目标点的水平角、俯仰角和斜距,并自动计算出目标点的坐标。
全站仪具有自动追踪和测距、测角、计算坐标的功能,可以大大提高测量的准确性和工作效率。
2. 光电测距法光电测距法是利用激光器发出的激光束,通过接收器接收反射光信号,并利用光电测距仪器测量出光的传播时间,从而计算出目标点的距离。
光电测距法适用于近距离和中距离测量,具有测量快速、准确度高的特点。
3. EDM法EDM法是一种利用电波来测量距离的方法。
它通过同步发射和接收电波信号的方式,通过时间差测量、电磁波测距、频率相位差测距等方式,可以测量出目标点的距离。
EDM法适用于较远距离测量,并具有较高的测量精度。
4. 视测法视测法是一种利用观测器用目视观测目标点,根据几何关系计算出目标点的位置坐标的方法。
在视测法中,观测器需要准确的辨别目标点,并通过仪器记录下观测结果,然后进行计算。
视测法适用于近距离、中距离的目标点测量,具有无需仪器、直接可视等特点。
5. 梯形测量法梯形测量法是一种利用三角形的相似性原理进行测量的方法。
它通过在目标点上设置测量基线,然后利用测量仪器分别测量出目标点到基线两侧的距离,利用三角函数和相似三角形的关系计算出目标点的位置坐标。
梯形测量法适用于小面积平面测量和高精度测量。
以上是几种常见的点平面测设方法,它们各有优势和适用场景,可以根据实际情况选择合适的测量方法进行使用。
这些方法在工程测量、地理测量等领域发挥着重要的作用,能够为工程建设、地质勘探等提供准确的测量数据。
点的平面位置的测设方法
点的平面位置的测设方法有直角坐标法、极坐标法、角度交会法和距离交会法。
至于采用那种方法,应根据控制网的形式、地形情况、现场条件及精度要求等因素确定。
一、直角坐标法
直角坐标法是根据直角坐标原理,利用纵横坐标之差,测设点的平面位置。
直角坐标法适用于施工控制网为建筑方格网或建筑基线的形式,且量距方便的建筑施工场地。
1.计算测设数据
如图10-7所示,Ⅰ、Ⅱ、Ⅲ、Ⅳ为建筑施工场地的建筑方格网点,a 、b 、c 、d 为欲测设建筑物的四个角点,根据设计图上各点坐标值,可求出建筑物的长度、宽度及测设数据。
m 00.50m 00.530m 00.580=-=-=a c y y 建筑物的长度 m 00.30m 00.620m 00.650=-=-=a c x x 建筑物的宽度
测设a 点的测设数据(Ⅰ点与a 点的纵横坐标之
x :700.00m x :650.00m x :620.00m x :600.00m y :600.00m
y :580.00m y :530.00m
y :500.00m
a b
c
d m
n
Ⅰ Ⅱ
Ⅲ
Ⅳ
图10-7 直角坐标法
差):
-
620=
.
-
∆I x
x a
x
00
=
=
20
.
m
m
m
00
00
.
600
=
-
530=
-
∆I y
.
y a
y
=
00
.
00
m
30
m
m
00
500
.
2.点位测设方法
(1)在Ⅰ点安置经纬仪,瞄准Ⅳ点,沿视线方向测设距离30.00m,定出m点,继续向前测设50.00m,定出n点。
(2)在m点安置经纬仪,瞄准Ⅳ点,按逆时针方向测设90˚角,由m点沿视线方向测设距离20.00m,定出a点,作出标志,再向前测设30.00m,定出b点,作出标志。
(3)在n点安置经纬仪,瞄准Ⅰ点,按顺时针方向测设90˚角,由n点沿视线方向测设距离20.00m,定出d点,作出标志,再向前测设30.00m,定出c点,作出标志。
(4)检查建筑物四角是否等于90˚,各边长是否
等于设计长度,其误差均应在限差以内。
测设上述距离和角度时,可根据精度要求分别采用一般方法或精密方法。
二、极坐标法
极坐标法是根据一个水平角和一段水平距离,测设点的平面位置。
极坐标法适用于量距方便,且待测设点距控制点较近的建筑施工场地。
图10-8 极坐标法
1.计算测设数据
如图10-8所示,A 、B 为已知平面控制点,其坐标值分别为A (x A ,y A )、B (x B 、y B ),P 点为建筑物的一个角点,其坐标为P (x P 、y P )。
现根据A 、B 两点,用极坐标法测设 P 点,其测设数据计算方法如下:
(1)计算AB 边的坐标方位角αAB 和AP 边的坐标方位角αAP 按坐标反算公式计算。
AB AB
AB
x y ∆∆=arctan
α
AP AP
AP
x y ∆∆=arctan
α
注意:每条边在计算时,应根据∆x 和∆y 的正负情况,判断该边所属象限。
(2)计算AP 与AB 之间的夹角。
AP AB ααβ-=
(3)计算A 、P 两点间的水平距离。
2
222)()(AP AP A P A P AP y x y y x x D ∆+∆=-+-=
例10-1 已知x P =370.000m ,y P =458.000m ,
x A =348.758m ,y A =433.570m ,αAB =103˚48′48″,试计算测设数据β和D AP 。
解
439548m 758.348m 000.370m
570.433m 000.458arctan arctan '
''︒=--=∆∆=AP AP AP
x y α
4194544395488484103'''︒='''︒-'''︒=-=AP AB ααβ
37
.32m )570.433m 000.458(m )758.348m 000.370(22=-+-=AP D 2.点位测设方法
(1)在A 点安置经纬仪,瞄准B 点,按逆时针方向测设β角,定出AP 方向。
(2)沿AP 方向自A 点测设水平距离D AP ,定出P 点,作出标志。
(3)用同样的方法测设Q 、R 、S 点。
全部测设完毕后,检查建筑物四角是否等于90˚,各边长是否等于设计长度,其误差均应在限差以内。
同样,在测设距离和角度时,可根据精度要求分别采用一般方法或精密方法。
三、角度交会法
角度交会法适用于待测设点距控制点较远,且量距较困难的建筑施工场地。
1.计算测设数据
如图10-9a 所示,A 、B 、C 为已知平面控制点,P 为待测设点,现根据A 、B 、C 三点,用角度交会法测
a )
b )
图10-9 角度交会法
设P点,其测设数据计算方法如下:
(1)按坐标反算公式,分别计算出αAB、αAP、αBP、αCB和αCP。
(2)计算水平角β1、β2和β3。
2.点位测设方法
(1)在A、B两点同时安置经纬仪,同时测设水平角β1和β2定出两条视线,在两条视线相交处钉下一个大木桩,并在木桩上依AP、BP绘出方向线及其交点。
(2)在控制点C上安置经纬仪,测设水平角β3,同样在木桩上依CP绘出方向线。
(3)如果交会没有误差,此方向应通过前两方向线的交点,否则将形成一个“示误三角形”,如图10-9b 所示。
若示误三角形边长在限差以内,则取示误三角形重心作为待测设点P的最终位置。
测设β1、β2和β3时,视具体情况,可采用一般方法和精密方法。
四、距离交会法
距离交会法是由两个控制点测设两段已知水平距离,交会定出点的平面位置。
距离交会法适用于待测设点至控制点的距离不超过一尺段长,且地势平坦、量距方便的建筑施工场地。
图10-10 距离交会法。