第五章 信息光学基础
- 格式:doc
- 大小:445.50 KB
- 文档页数:12

光信息处理(信息光学)复习提纲第一章线性系统分析1.空间频率的定义是什么?如何理解空间频率的标量性和矢量性?2.空间频率分量的定义及表达式?3.平面波的表达式和球面波的表达式?4.相干照明下物函数复振幅的表示式及物理意义?5.非相干照明下物光强分布的表示式及物理意义?6.线性系统的定义7.线性系统的脉冲响应的表示式及其作用8.何谓线性不变系统9.卷积的物理意义10.线性不变系统的传递函数及其意义11.线性不变系统的本征函数第二章标量衍射理论1.衍射的定义2.惠更斯-菲涅耳原理3.衍射的基尔霍夫公式及其线性表示4.菲涅耳衍射公式及其近似条件5.菲涅耳衍射与傅立叶变换的关系6.会聚球面波照明下的菲涅耳衍射7.夫琅和费衍射公式8.夫琅和费衍射的条件及范围9.夫琅和费衍射与傅立叶变换的关系10.矩形孔的夫琅和费衍射11.圆孔的夫琅和费衍射(贝塞尔函数的计算方面不做要求)12.透镜的位相变换函数13.透镜焦距的判别14.物体位于透镜各个部位的变换作用15.几种典型的傅立叶变换光路第三章光学成象系统的传递函数1.透镜的脉冲响应2.相干传递函数与光瞳函数的关系3.会求几种光瞳的截止频率4.强度脉冲响应的定义5.非相干照明系统的物象关系6.光学传递函数的公式及求解方法7.会求几种情况的光学传递函数及截止频率第五章光学全息1.试列出全息照相与普通照相的区别2.简述全息照相的基本原理3.试画出拍摄三维全息的光路图4.基元全息图的分类5.结合试验谈谈做全息实验应注意什么(没做过实验,只谈一些理论性的注意方面)6.全息照相为什么要防震,有那些防震措施,其依据是什么7.如何检测全息系统是否合格8.全息照相的基本公式9.全息中的物像公式及解题(重点)复 习第一章 线性系统分析1.空间频率的定义是什么?如何理解空间频率的标量性和矢量性?时间量 空间量22v T πωπ==22K f ππλ== 时间角频率 空间角频率其中:v ----时间频率 其中:f ---空间频率T----时间周期 λ-----空间周期 物理意义:由图1.7.3知:(设光在z x ,平面内传播,0=y )cos xd λα=, 又 ∵ 1x xf d =联立得:cos x f αλ=讨论:① 当090,,<γβα时0,,>z y x f f f ,表示k沿正方向传播;②标量性,当α↗时,αcos ↘→x f ↘→x d ↗当α↘时,αcos ↗→x f ↗→x d ↘ ③标量性与矢量性的联系条纹密x d ↘→x f ↗→α↘→θ↗x x f d 1=λαcos =x f 条纹疏x d ↗→x f ↘→α↗→θ↘2.空间频率分量的定义及表达式?{}γβαcos ,cos ,cos k k ={}z y x r ,,=)cos cos cos (γβαz y x k r k ++=⋅代入复振幅表达式:()()()[]γβαμcos cos cos ex p ,,,,0z y x jk z y x z y x U ++=()⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛++=z y x j z y x λγλβλαπμcos cos cos 2exp ,,0 ()()[]z f y f x f j z y x z y ++=λπμ2ex p ,,0式中:λαcos =x f ,λβcos =yf ,λγcos =z f3.平面波的表达式和球面波的表达式?平面波()⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛++=z y x j z y x U λγλβλαπμcos cos cos 2exp ,,0 ()()[]z f y f x f j z y x U z y x ++=πμ2ex p ,,0球面波()1,,jkr a U x y z e γ=()21212212121221⎪⎪⎭⎫ ⎝⎛++=++=z y x z z y x r近轴时()1,,U x y z ⎥⎥⎦⎤⎢⎢⎣⎡⎪⎪⎭⎫⎝⎛++=1221021exp z y x jkz r a()⎪⎪⎭⎫ ⎝⎛+⋅≈1221102exp exp z y x jkjkz z a ⎪⎪⎭⎫ ⎝⎛+=12202exp z y x jkU若球面波中心不在坐标原点,上式改为:()1,,U x y z ()()⎥⎥⎦⎤⎢⎢⎣⎡++-=1202002exp z y y x x jk U4.相干照明下物函数复振幅的表示式及物理意义?设()y x f ,为一物函数的复振幅,其傅氏变换对为 ()()(),exp 2x y x y F f f f x y j f x f y dxdyπ∞-∞⎡⎤=-+⎣⎦⎰⎰ ()()(),exp 2x yxyxyf x y F f f j f x f y df dfπ∞-∞⎡⎤=+⎣⎦⎰⎰可见:物函数()y x f ,可以看作由无数振幅不同()x y x y F f f df df 方向不同()cos ,cos xyf f αλβλ==的平面波相干迭加而成。






湖北省高等教育自学考试大纲课程名称:信息光学课程代码:7076第一部分课程性质与目标一、课程性质与特点信息光学是应用光学、计算机和信息科学相结合而发展起来的一门新的光学学科,是信息科学的重要组成部分,也是现代光学的核心。
本课程主要从两个方面介绍信息光学的基本内容:一是信息光学的基础理论,包括线性系统理论、标量衍射理论、传递函数理论等;二是信息光学的主要应用,包括光学全息、计算全息、空间滤波、光学相干和非相干处理等。
二、课程目标与基本要求通过本课程的教学,使学生了解和掌握光信息科学的基本理论及基本技术,了解光信息科学的实际应用,培养学生理论联系实际,开拓学生理论用于实践的方法和创新思路,提高学生解决实际问题的能力。
三、与本专业其他课程的关系《信息光学》是光机电一体化工程专业的一门专业课,其先修课程主要包括普通物理、高等数学、傅立叶变换、光学等课程。
第二部分考核内容与考核目标第一章线性系统分析一、学习目的与要求本章基本内容为:常用数学函数,卷积与相关,傅立叶变换性质及定理,线性系统分析,二维光波场分析。
本章是本课程的基础,要求学生在解决光学问题中能熟练运用其性质和定理,线性系统与光学系统的关联,加深对空间频率、空间频谱概念的理解。
二、考核知识点与考核目标(一)(重点)识记:常用数学函数;卷积;互相关、自相关;傅立叶变换;线性系统;线性平移不变系统理解:傅立叶变换性质;线性系统分析;空间频率、空间频谱;应用:单色平面波空间频率的计算(二)(次重点)识记:卷积、相关的性质;理解:傅立叶变换基本定理第二章标量衍射理论一、学习目的与要求本章基本内容为:基尔霍夫积分定理;基尔霍夫衍射公式;菲涅耳衍射和夫朗和费衍射;透镜的傅立叶变换特性。
本章是教学的重点,是信息光学的基础,要求学生掌握标量波衍射理论,侧重利用菲涅耳衍射与卷积、夫朗和费衍射与傅立叶变换关系解决问题;掌握光波通过透镜的相位分布,透镜的傅立叶变换特性及孔径对透镜实现傅立叶变换的影响。


《信息光学》课程教学大纲一、课程基本信息二、课程简介信息光学是应用光学、计算机和信息科学相结合而发展起来的一门新的光学学科,是信息科学的一个重要组成部分,也是现代光学的核心。
本课程主要介绍信息光学的基础理论及相关的应用,内容涉及二维傅里叶分析、标量衍射理论、光学成像系统的频率特性、部分相干理论、光学全息照相、空间滤波、相干光学处理、非相干光学处理、信息光学在计量学和光通信中的应用等。
三、课程目标本课程是光电信息科学与工程专业的主要专业课程之一,设置本课程的目的是让学生掌握信息光学的基本概念、基础理论及光信息处理的基本方法,了解光信息处理的发展近况和运用前景。
为今后从事光信息方面的生产,科研和教学工作打下基础。
四、教学内容及要求第一章信息光学概述(2学时)1.信息光学的基本内容和发展方向2.光波的数学描述和基本概念3.相干光和非相干光4.从信息论看光波的衍射要求:1.了解信息光学的内容和发展方向2.掌握相干光和非相干光的特点3.掌握从信息论的观点看光波的衍射。
重点:空间频率,等相位面。
从信息光学看衍射的基本观点。
难点:空间频率,光波的数学描述。
第二章二维傅里叶分析(8+2学时)1.光学常用的几种非初等函数2.卷积与相关3.傅里叶变换的基本概念4.线性系统分析5.二维采样定理要求:1.了解光学中常用非初等函数的定义、性质,熟悉它们的图像及在光学中的作用2.了解卷积与相关的定义及基本性质3.熟悉傅里叶变换的基本原理,性质和几何意义4.熟悉系统的基本概念及线性系统分析的基本理论5.了解二维采样定理及其应用6.本章强调概念的物理意义理解,以定性和应用为主。
避免与《信号与系统》课程重复。
重点:δ函数的意义和运算特性,傅里叶变换性质、定理,相关和卷积的意义及运算,线性空间不变系统的特性。
难点:卷积,傅里叶变换、系统分析。
第三章标量衍射理论(6+2学时)1.基尔霍夫衍射理论2.菲涅耳衍射和夫琅和费衍射3.夫琅和费衍射计算实例4.菲涅尔衍射计算实例5.衍射的巴俾涅原理要求:1.了解基尔霍夫衍射理论2.熟悉菲涅耳- 基尔霍夫衍射公式及其物理意义3.熟悉菲涅耳衍射与夫琅和费衍射4.掌握常见夫琅和费衍射光场的分析与计算5.了解菲涅耳衍射光场的分析和计算6.了解巴俾涅原理及其应用重点:如何用二维傅里叶变换来分析和计算夫琅和费衍射。
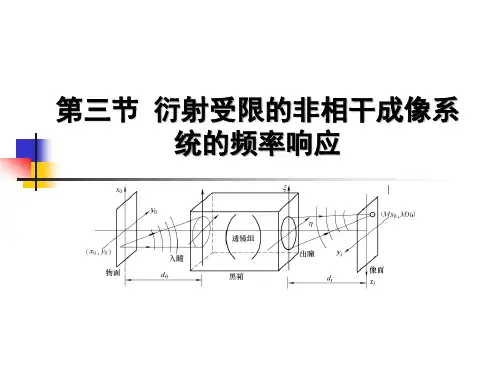
第五章傅里叶变换光学与相因子分析方法5.1 衍射系统波前变换◆引言现代光学的重大进展之一,是引入“光学变换”概念,由此发展而形成了光学领域的一个新分支——傅里叶变换光学,泛称为变换光学(transform optics),也简称为博里叶光学,它导致了光学信息处理技术的兴起.现代变换光学是以经典波动光学的基本原理为基础,是干涉、衍射理论的综合和提高,它与衍射、尤其与夫琅禾费衍射息息相关.对于熟悉经典波动光学的人们来说,由于他们有着较充分的概念储备和较充实的物理图像,因而具备更为有利的条件,去深刻而灵活地掌握现代变换光学.◆衍射系统及其三个波前如图所示,一个衍射系统以衍射屏为界被分为前后两个空间.前场为照明空间,充满照明光波;后场为衍射空间,充满衍射光波.照明光波比较简单、常为球面波或平面波,这两种典型波的等幅面与等相面是重合的,属于均匀波,其波场中没有因光强起伏而出现的图样.衍射波较为复杂,它不是单纯的一列球面波或一列平面波,其等幅面与等相面—般地不重合,属于非均匀波,其波场中常有光强起伏而形成的衍射图样.在衍射系统的分析中,人们关注三个场分布:其中,入射场是照明光波到达衍射屏的波前函数;出射场是衍射屏的透射场或反射场,它是衍射空间初端的波前函数,它决定了整个衍射空间的光场分布;而衍射场是纵向特定位置的波前函数。
由此可见,整个衍射系统贯穿着波前变换:波前这是衍射屏的作用:波前这是波的传播行为.由一个波前导出前方任意处的另一个波前,这是波衍射问题的基本提法,亦即波传播问题的基本提法.标量波的传播规律己由惠更斯—菲涅耳—基尔霍夫理论(HFK 理论)给出.在常见的傍轴情形下,其表达式为其积分核为,这是一个球面波的相因子形式.换言之HFK理论是—个关于衍射的球面波理论——衍射场是衍射屏上大量次波点源所发射的球面被的相干叠加.◆衍射屏函数及其三种类型我们已经同多种衍射屏有过交道,现在给山衍射屏函数的一般性定义,以定量地描述衍射屏的自身特征:即,屏函数(screen function)等于出射波前函数与入射波前函数之比.对于透射屏,可称作复振幅透过率函数;对于反射屏,可称作复振幅反射率函数.无疑,屏函数通常也是复函数,含模函数和辐角函数.唯象地看,实际上的衍射屏可分为三种类型,振幅型、相位型和相幅型.若为常数,仅有函数,则该衍射屏为振幅型,凡孔型衍射屏均系振幅型.若为常数,仅有函数,则该衍射屏为相位型,这在此之前似乎少见,其实,闪耀光栅不论其为透射的或反射的,均是一个相位型衍射屏,下一节即将研究的透镜相位衍射元件.当然,更为一般的情况是相幅型衍射屏,、皆为函数形式,即不仅出射场的振幅分布有别于入射场的,而且出射场的相位分布也有别于入射场的。
第五章 光学信息处理基础光学信息处理是在全息术、光学传递函数和激光的基础上,将数学中的傅里叶变换和通信中的线性系统理论引入到光学,用光学的方法实现傅立叶变换,在频域中描述和处理光学信息。
傅立叶分析的方法早在十九世纪末、二十世纪初成功地应用于光学领域,具有代表性的是阿贝关于显微镜的两次成像理论和阿贝-波特实验。
上个世纪三十年代泽尼克发明的相衬显微镜是光学信息处理的早期卓越成就。
激光器的出现为人们提供了相干性非常好的光源,光学信息处理得到迅速发展,例如用光学的方法实现相关运算、特征识别微分运算等。
本章主要内容:1波前变换;2阿贝成像原理和相衬显微镜;3傅里叶变换;4傅立叶变换光学及光学信息处理;5光学全息照相;§1 波前变换(Wave front transformation) 1.1 对衍射的再认识前面我们把光经过障碍物后偏离传播的现象称为衍射。
应用惠更斯-菲涅耳原理讨论了光的衍射问题后,我们意识到光的衍射是光在传播的过程中波面受到某种限制,即自由传播波面被破坏,这便是衍射。
按照惠更斯-菲涅耳原理,只要将波前()0U Q 上每一面元看成次波中心,把它们对空间某一点的贡献相干叠加,就能求衍射场的分布()U P ,并且波前()U P 由()0U Q )唯一的确定。
上述意味着,在Σ上有障碍物存在,使得Σ上波前函数()0U Q )发生了与自由传播有所不同的变化,光波场就会产生重新分布,这就是衍射的实质。
1.2 衍射系统的屏函数(screen function)按照前面我们对光的衍射认识,凡能改变波前上的复振幅的物体称为衍射屏(diffractionfunction )。
衍射屏可以是透射物体,也可以示反射物体,有各种形状。
光波经过衍射屏是光的传播问题,要用菲涅耳-基尔霍夫积分公式计算,把这种衍射看作是一种变换,衍射屏能将输入波前()in U x,y %转化为波前()outU x,y %,衍射屏可用以下一个函数表征。
()()(),,,out inU x y T x y U x y =屏函数包括振幅和相位两部分,通常有以下三种 ① 相位型 ② 振幅型 ③ 振幅相位型任何形状的孔或遮光屏是最简单的振幅型透射衍射屏,他们的函数具有如下形式()10,T x,y ,ìïï=íïïî% 透镜是常见的相位型衍射屏。
0ϕπ-1.3平面波的波前函数一个沿k方向传播的平面波,在x-y 平面上的复振幅可表示为(exp U r A j k r ϕ⎡⎤=+ (6-1)波场中空间任意点P 的相位落后于O 的相位为()()P O k r ϕϕϕ∆=-=式中r OP =,()()12cos cos cos cos x y k r k x k y k x y k x y αβθθ=+=+=+式中cos ,cos αβ分别是波矢k的方向余弦,1θ和2θ分别是α和β的余角,从而有()()()12cos cos P k x y O ϕθθϕ=++,可以看出平面波前相位因子是x,y 的先行函数。
如图所示,平面波前上的等相位线是等间隔的平行线。
相位差为2π,1.3.2 球面波前函数球面波的振幅与p 点到源的距离r 成反比()jkr A Ur e r= (6-2) 透光部分 遮光部分(U %1.4 傍轴条件 远场条件(轴上物点)把前面的球面波前函数表达式运用到衍射问题上,我们可以去一些近似。
通常衍射装置中,点源或衍射屏上的次波源离轴线的横向距离0ρ=和接受屏上场点横向距离ρ=z 小的多,面前函数中的r 可展作幂级数开成。
()()220022222000022222000121222x x y y r z z x y xx yy x y z ...z z zxx yy x y r ...z z轾-+-犏=+犏犏臌轾+++犏=++-+犏臌++=+-+ (6-4) 波前中心o 到振源s 之间的距离r0为002202x y r zz+? (6-5)若点源在轴上,x0=y0 =0 上式化为222x y r z z+=+(6-6)会聚波发散波有两种近似条件:旁轴条件和远场条件 (1)旁轴条件220221,z zr r = (6-7) ()jkr A U r e r=%式中的振幅A/r 是r 的缓变函数,在旁轴条件下r 的二次项可以忽略,认为A/r ≈A/z ,在波前上是常数,而相位因子随r 是急剧震荡的函数,不能忽略二次项。
所以旁轴条件下的波前 函数表示为()02200,exp exp 2jkr xx yy Ae x y U x y jk jk z z z ⎛⎫++⎛⎫≈ ⎪ ⎪⎝⎭⎝⎭ (6-8) 会聚球面波的波前函数则为()022*00,exp exp 2jkr xx yy Ae x y U x y jk jk z z z -⎛⎫++⎛⎫≈-- ⎪ ⎪⎝⎭⎝⎭ (6-9) 对于轴上点()022,exp 2jkr Ae x y U x y jk z z ⎛⎫+≈ ⎪⎝⎭(6-10)()022*,exp 2jkr Ae x y U x y jkz z -⎛⎫+≈- ⎪⎝⎭(6-11) (2) 远场条件源点202ρπ k z 或20zρλ , 场点22k z ρπ 或2ρλ z 通常衍射装置 很难满足上述条件的尤其是场点很难满足远场条件。
若只有源点满足远场条件,则有r0≈z ,于是(12),(13)式化为()2200,exp exp 2jkz xx yy Ae x y U x y jk jk z z z ⎛⎫++⎛⎫≈ ⎪ ⎪⎝⎭⎝⎭ (6-14)()22*00,exp exp 2jkz xx yy Ae x y U x y jk jk z z z -⎛⎫++⎛⎫≈-- ⎪ ⎪⎝⎭⎝⎭ (6-15)1.5 透镜的相位变换函数在透镜的前后各取一平面Σin 和 Σout ,设在它们上面的输入波前函数和输出波前函数分别是()()()()()()ϕϕ⎧=⎪⎨=⎪⎩ in out j x,y in in j x,y outout U x,y A x,y eU x,y A x,y e (6-16)我们可以把透镜看作一个相位型透射屏,现计算它的屏函数()()ϕ= L j x,y LT x,y Ke (6-17)通常透镜的投射率很高,k 近似等于1,即k=Aout/Ain ≈1严格计算 φL(x,y)= φout (x,y)-φin(x,y)是困难的,现在旁轴条件下计算由于透镜很薄,入射点和出射点的坐标很相近,光程可以近似沿平行于光轴方向计算()()()()()()120121ϕ=∆+∆+⎡⎤⎣⎦=--∆+∆⎡⎤⎣⎦L x,y k x,y x,y nd x,y k nd n (6-18)其中 d0=d+ Δ1+Δ2=透镜中心厚度,与x,y 无关,常 可以略去不写,Δ1 和 Δ2分别可以写成()()()221112222222+∆=-≈+∆=--≈-x y x, y r r x y x, y r r (6-19)r1 和r2分别是透镜前后表面的曲率半径。
()()22221211122L n x y x,y k x y kr r Fϕ⎛⎫-+=--+=- ⎪⎝⎭(6-20)于是透镜的屏函数为,Q '2()222L x y T x,y exp jk F ⎛⎫+=- ⎪⎝⎭ (6-21)式中F 正是前面几何光学讨论过的透镜焦距公式,如果入射波为平行于光轴的平面波,即出射为()()()()222out in LU x,y U x,y T x,y x y U o exp jk F =⎛⎫+=- ⎪⎝⎭(6-22)上式代表会聚到距透镜为F 的球面波,如果入射波是由s 发出发散球面波()222jkz inAe x y U x,y exp jk z s ⎛⎫+= ⎪⎝⎭ (6-23)出射波为()()()22222222112out in Ljkz jkz U x,y U x,y T x,y Ae x y x y exp jkexp jk z F s Ae x y exp jkz F s =⎛⎫⎛⎫++=- ⎪ ⎪⎝⎭⎝⎭⎛⎫+⎛⎫=-- ⎪ ⎪⎝⎭⎝⎭(6-24)令111s F s=-' ()222jkz out Ae x y U x,y exp jk z s ⎛⎫+=- ⎪'⎝⎭ (6-25)上式代表会聚到透镜后轴上距离为s ’处的球面波。
1.6 棱镜的相位变换函数棱镜的作用不是成像,是让光方向发生偏折,将一束平行光变换成另一束平行光,平行光的相位子为线性,因此棱镜相位变因子应该为线性。
对于楔形棱镜可近似认为光线在两界面上等高。
设棱角为α,折射率为n ,则相位差为()()()()()01p x ,y k x ,yn d x ,y k n d n x ,yϕ=∆+⎡⎤⎣⎦=--∆⎡⎤⎣⎦(6-26)式中knd 0是常量,可以略去。
则()()1p x,y k n x ϕα=-()()1p T x,y exp jk n x α⎡⎤=--⎣⎦(6-27) 以上计算是针对一维情况,对二维有()()()121p T x,y exp jk n x y αα⎡⎤=--+⎣⎦(6-28) 如果入射波是来自于点源Q 的球面波()222jkz inAe x y U x,y exp jk z s ⎛⎫+= ⎪⎝⎭(6-29) 我们知道,一个楔形棱镜位相变换函数是x 和y的作用就等效于一个棱镜 考虑透镜薄的位相变换函数, 出射波前函数为()()()[]221212αα=⎛⎫+=--+ ⎪⎝⎭out in PjkzU x,y U x,y Tx,y Ae x y exp jkexp k(n )(x y )z s(6-30) 出射波是轴外点源Q’发出的发散球面波,点源的位置由线性相因子系数决定()()010211x n sy n sαα⎧=-⎪⎨=-⎪⎩ (6-31) §2 阿贝成像原理 2.1 阿贝成像原理传统成像的观点是物和像的对应关系是点对点。
另一种观点,着眼于频谱的变换:物是一系列不同空间频率信息的集合,相干成像分成两步。
相干入射光经过物平面发生夫琅和费衍射,在透镜后焦面上形成一系列衍射斑。
第二步是干涉,衍射斑发出的球面波在像平面上相干叠加,像就是干涉场。
这种成像的理论就是阿贝成像原理。
因为任何图像都可以作傅里叶 展开,最基本的图像是单频信息的正弦光栅。
Q 'A 'CinoutU U设光栅的空间周期为d ,空间频率f ,f=1/d ,正弦光栅的 波前为()()()2212112o j fx j fx U x,y A cos fx A e e πππ-⎡⎤=+⎣⎦⎡⎤=++⎢⎥⎣⎦(6-32) 与平面波前()()()120U x,y U exp k x sin y sin q q 轾=+臌%%相比较 上式代表三列平面波,方向分别在0 =0θ,±sin =2/k f θπ±三列波被透镜接受,在后焦面上形成三个夫琅和费衍射斑S 0 ,S ±,像面上的场是三个衍射斑的相干叠加。