信息光学基础1-3卷积

信息光学公式 1·矩形函数⎪⎩⎪⎨⎧≤-=⎪⎭⎫ ⎝⎛-其它,021,100a x x a x x rectF { a sinc(a x ) } = rect(f /a )F ⎪⎭⎫ ⎝⎛Λ=b f b 1(bx)}{sinc22·inc s 函数()()a x x a x x a 000sin x x sinc --=⎪⎭⎫ ⎝⎛-ππ 3·三角形函数 ⎪⎩⎪⎨⎧≤-=⎪⎭⎫ ⎝⎛Λ其它,0,1a x a xa x4·符号函数()⎪⎩⎪⎨⎧<-=>=0,10,00,1sgn x x x x5·阶跃函数()⎩⎨⎧<>=0,00,1x x x step6·圆柱函数⎪⎩⎪⎨⎧<+=⎪⎪⎭⎫⎝⎛+其它,0,12222ayx a y x circ极坐标内⎩⎨⎧><=⎪⎭⎫ ⎝⎛ar o a r a r ,,1circ7·δ函数的定义 普通函数形式的定义()()⎪⎪⎭⎪⎪⎬⎫=⎩⎨⎧==∞≠≠=∞∞-⎰⎰1,0,0,0,0,dxdy y x y x y x y x δδ广义函数形式的定义()()()0,0,,φφδ=∞∞-⎰⎰dxdy y x y x其中()y x ,φ在原点处连续 δ函数的性质设函数()y x f ,在()00,y x 点出连续，则有 筛选性质()()()y x f dxdy y y x x y x f ,,,00=--∞∞-⎰⎰δ坐标缩放性质 ()()y x abby ax ,1,δδ=可变性 ()()()y x y x δδδ=, 8·梳状函数性质()()()∑∑∞-∞=∞∞-=-=m nx j m x x πδ2exp comb()∑∞∞-∆-∆=⎪⎭⎫ ⎝⎛∆x m x x x x δcomb()∑∞-∞=⎪⎭⎫⎝⎛∆-∆=∆m xm x x δ1xx comb ()()ξcomb x comb −−→←ℑ()ξx comb x x comb ∆∆−−→←⎪⎭⎫ ⎝⎛∆ℑx ()()()y x comb comb y x,comb =9·傅里叶变换()()(){}dxdy y x j y x f F ηξπηξ+-=∞∞-⎰⎰2exp ,, ()()()[]ηξηξπηξd d y x j F y x f +=∞∞-⎰⎰2exp ,,10·阶跃函数step(x)的傅里叶变换(){}(){}()⎭⎬⎫⎩⎨⎧-=+=ℑℑπξξδj 21x sgn 121x step11·卷积的定义()()()()()x h x f d x h f x g *=-=⎰∞∞-ααα定义()x f 和()x h 的二维卷积：()()()()()y x h y x f d d y x h f y x g ,*,,,,=--=⎰⎰∞∞-βαβαβα卷积的几个重要性质： 线性性质：{),(),(),(),(),()},(),(y x g y x bh y x g y x af y x g y x bh y x af *+*=*+卷积符合交换律：,(),(),(),(y x f y x h y x h y x f *=*卷积符合结合律：[][]),(),(),(),(),(),(y x g y x h y x f y x g y x h y x f **=**卷积的坐标缩放：若),(),(),(y x g y x h y x f =*，则),(1),(),(by ax g abby ax h by ax f =*（a,b 均不等于0）卷积位移不变性：若),(),(),(),(y x f y x h y x h y x f *=*，则),(),(),(),(),(000000y y x x g y y x x h y x f y x h y y x x f --=--*=*--函数),(y x f 与δ函数的卷积： ),(),(),(0000y y x x f y y x x y x f --=--*δ12·米尔对称性()()ηξηξ--=*,,FF13·卷积定理()()()x rect x rect *=Λx(){}(){}(){}()ξ2sinc x rect x rect ==Λℑℑℑx()(){}()()()ξξξrect rect rect sin x sinc ==*ℑx c()()(){}()x sinc rect sinc sinc 1==*-ℑξx x14·线性平移不变系统()()()()()y x h y x f d d y x h f y x g ,,,,,*=--=∞∞-⎰⎰βαβαβα15·函数变换输入函数 ()()y x y x f 002cos ,ηξπ+= 其频谱函数()()()[]0000,,21,ηηξξδηηξξδηξ-++--=F16·单色光波场的复振幅复振幅 ()()r k j ra P U *=exp 0光强 *==UU UI 217·X 方向的空间频率的相关公式等相线位方程 c kx =αcos λπ2=k αλc o s =X X 方向的空间频率λαξcos 1==X 18·整个空间的空间频率()()[]z y x j a Z Y X U ζηξπ++=2exp ,, 221λζηξ=++2219·泰伯效应()()jkz d n c n nG exp ⎪⎭⎫ ⎝⎛-=∑∞-∞=ξδξ 泰伯距离 λ22dz T =20·相干截止频率 f D λρ2c =非相干截止频率 f D λρρ22c oc == 21·相干面积 ()()SSC A Z A Ω≈=λλ2第二章2·1夫琅禾费近似()()()()⎥⎦⎤⎢⎣⎡+-⎥⎦⎤⎢⎣⎡+=y y x x z k j y x z k j zj jkz y x y x h 002200exp 2exp exp ,,λ； 2·2菲涅尔衍射()()()()()0020200002exp ,exp ,dy dx z y y x x jk y x U zj jkz y x U ⎥⎥⎦⎤⎢⎢⎣⎡-+-=∞∞-⎰⎰λ傅里叶变换()()()()()()00002020000222exp 2exp ,2expexp1,dy dx y y xx z jy x z k j y x Uy x z k j jkz zj y x U ⎥⎦⎤⎢⎣⎡+-⨯⎥⎦⎤⎢⎣⎡+⨯⎥⎦⎤⎢⎣⎡+=∞∞-⎰⎰λπλ2·3透镜系统（1）输入平面位于透镜前焦面 这时f d =0得 ()()000000exp ,,dy dx f y y x x jk y x t c y x U ⎪⎪⎭⎫⎝⎛+-'=∞∞-⎰⎰ （2）输入面紧贴透镜 这时00=d 得 ()()00000022exp ,2exp ,dy dx q y y x x jk y x t qy x jk c y x U ⎪⎪⎭⎫ ⎝⎛+-⎪⎪⎭⎫ ⎝⎛+'=∞∞-⎰⎰ （3）物在透镜后方()()()0000000022exp ,2exp ,dy dx d q y y x x jk y x t d q y x jk c y x U ⎪⎪⎭⎫⎝⎛-+-⎥⎦⎤⎢⎣⎡-+'=∞∞-⎰⎰ 4·1希尔伯特变换可看成是一个线性平移不变系统，该系统的脉冲响应为t t h π1)(-= 而 )()()(t u t j t t u r *⎥⎦⎤⎢⎣⎡+=πδ脉冲响应对应的传递函数为()()νπνn j t F H sg 1=⎭⎬⎫⎩⎨⎧-=4·2互相干函数时间的平均值⎰-∞→=TTT dt t f Tt f )(21lim)(光场的互相干函数())(,),(),(),(12**2*12211ττΓ=+--t P u t P u t t P u t t P u *＝光场的自相干函数)(),(),(111*1ττΓ+＝t P u t P u复相干度()()()()()21122/122111212]00[I I τττγΓ=ΓΓΓ=Q 点的光强为()()()()(){}τγ122121Re 2)(I Q I Q I Q I Q I Q ++=干涉条纹的可见度为min ma x m i n m a x I I I I +-=V ()()()()()τγ1221212Q I Q I Q I Q I +=Imax 和Imin 是Q 点附近干涉条纹的极大值和极小值()()()()()()()()Q I Q I Q I Q I I Q I Q I Q I Q I I 2121min 2121max 22-+=++=光源的光谱密度分布 ()()()()⎥⎥⎦⎤⎢⎢⎣⎡=⎥⎦⎤⎢⎣⎡=∞→∞→2T 2T2*,lim ,,lim v P v P v P v T T TTT U U UG相干时间vc ∆=1τ 相干长度c c c l τ= 时间延迟t ＝2h/c4·3确定像点坐标：i z 为正表示发散球面波，i z 为负表示会聚球面波1012121-⎪⎪⎭⎫ ⎝⎛±=z z z z r p i λλλλ p pi r i i i x z zx z z x z z x +±=2120012λλλλp pi r i i i y z z y z z y z z y +±=2120120λλλλ4.4)⎪⎪⎭⎫⎝⎛--=-±-⎰∞∞-A B AC A dx C Bx Ax 22exp 2exp π积分公式：4·5 范西泰特——策尼克定理()()()()[]()()()()βαβαβαβαλπβαψd d I d d y x z j I j y x I y x I y xy x y xy x J u ,2exp ,exp ,,,;,,;,221122112211∞∞-∞∞-⎰⎰⎰⎰⎥⎦⎤⎢⎣⎡∆+∆-==4·6 傅里叶透镜的截止频率、空间带宽积和视场 1. 截止频率 传播方向角u 最大为 ()()fD D fD D u 22211-=-≈相应的空间频率 f D D uuλλλξ2sin 1-=≈=传播方向角u 最小为 ()()fD D f D D v 22211+=+≈相应的空间频率 fD D v vλλλξ2sin 1+=≈=2.空间带宽积δξξ单频线宽频带宽度信息容道∆=NfD D λξξ12-==∆11D =δξ SW N =∆=δξξSW 就是空间带宽积3.视场 21DD =4正弦条件 ηλf u f h ==sin。

信息光学信息光学（傅立叶光学）是综合性大学、工科院校和高等师范院校近代光学、信息光学、激光、光电子等专业研究生和大学高年级的必修课，它是从事光学和光电子领域科学研究和产品开发人员必须的理论基础。

其主要内容一般包括傅立叶光学、标量衍射理论、透镜的性质、部分相干光理论、光学全息及光信息处理等。

限于本课程的课时限制，我们准备主要讲授傅立叶光学、透镜性质、标量衍射理论、部分相干光理论的内容本课程的主要内容讲授拟分八章。

第一章：数学预备知识；第二章：二维傅立叶分析；第三章：衍射理论基础；第四章：菲涅耳衍射、夫琅和费衍射；第五章：透镜的傅立叶变换特性与成象性质；第六章：成象光学系统的传递函数；第七章：部分相干光理论；主要参考书①黄婉云，傅立叶光学教程，北师大出版社，1984②羊国光，宋菲君，高等物理光学，中国科大出版社，1991③J. W. Goodman, 詹达三译，傅立叶光学导论，科学出版社，1976④朱自强等，现代光学教程，四川大学出版社，1990⑤卞松玲等，傅立叶光学，兵器工业出版社，⑥蒋秀明等，高等光学，上海交大出版社⑦M. 波恩，E. 沃耳夫，光学原理，科学出版社，1978⑧吕乃光等，傅立叶光学基本概念和习题⑨谢建平等，近代光学基础，中国科技大学出版社，1990第一章：数学预备知识为了方便后面的学习，我们复习一下有关的数学知识。

§1-1 几个常用函数一、 矩形函数（rectangle function ）1、一维矩形函数表达式为：⎪⎪⎩⎪⎪⎨⎧>-≤-=-21||021||1)(rect 000a x x a x x a x x其函数图形为：当x 0=0，a =1时，矩形函数为：⎪⎪⎩⎪⎪⎨⎧>≤=21||021||1)(rect x x x [此时rect(x )=rect(-x )]其图形为2、二维矩形函数表达式为：⎪⎪⎩⎪⎪⎨⎧>->-≤-≤-=-⋅-21||,21||021||,21||1)()(000000b y y a x x b y y a x x b y y rect a x x rect其函数图形为：二维矩形函数可以用来描述屏上矩形孔的透过系数。

信息光学习题答案第一章 线性系统分析1.1 简要说明以下系统是否有线性和平移不变性. （1）()();x f dxdx g =（2）()();⎰=dx x f x g （3）()();x f x g = （4）()()()[];2⎰∞∞--=αααd x h f x g（5）()()απξααd j f ⎰∞∞--2exp解：（1）线性、平移不变； （2）线性、平移不变； （3）非线性、平移不变； （4）线性、平移不变； （5）线性、非平移不变。

1.2 证明)()ex p()(2x comb x j x comb x comb +=⎪⎭⎫ ⎝⎛π证明：左边＝∑∑∑∞-∞=∞-∞=∞-∞=-=⎥⎦⎤⎢⎣⎡-=⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛n n n n x n x n x x comb )2(2)2(2122δδδ∑∑∑∑∑∑∞-∞=∞-∞=∞-∞=∞-∞=∞-∞=∞-∞=--+-=-+-=-+-=+=n nn n n n n n x n x n x jn n x n x x j n x x j x comb x comb )()1()()()exp()()()exp()()exp()()(δδδπδδπδπ右边当n 为奇数时，右边＝0，当n 为偶数时，右边＝∑∞-∞=-n n x )2(2δ所以当n 为偶数时，左右两边相等。

1.3 证明)()(sin x comb x =ππδ 证明：根据复合函数形式的δ函数公式0)(,)()()]([1≠''-=∑=i ni i i x h x h x x x h δδ式中i x 是h(x)=0的根，)(i x h '表示)(x h 在i x x =处的导数。

于是)()()(sin x comb n x x n =-=∑∞-∞=πδπππδ1.4 计算图题1.1所示的两函数的一维卷积。

解：设卷积为g(x)。

当-1≤x ≤0时，如图题1.1(a)所示， ⎰+-+=-+-=xx x d x x g 103612131)1)(1()(ααα图题1.1当0 < x ≤1时，如图题1.1(b)所示， ⎰+-=-+-=13612131)1)(1()(xx x d x x g ααα 即 ⎪⎪⎪⎩⎪⎪⎪⎨⎧≤<+-≤≤--+=其它,010,61213101,612131)(33x x x x x x x g 1.5 计算下列一维卷积。

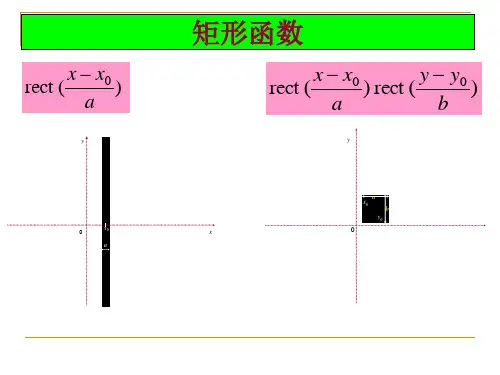
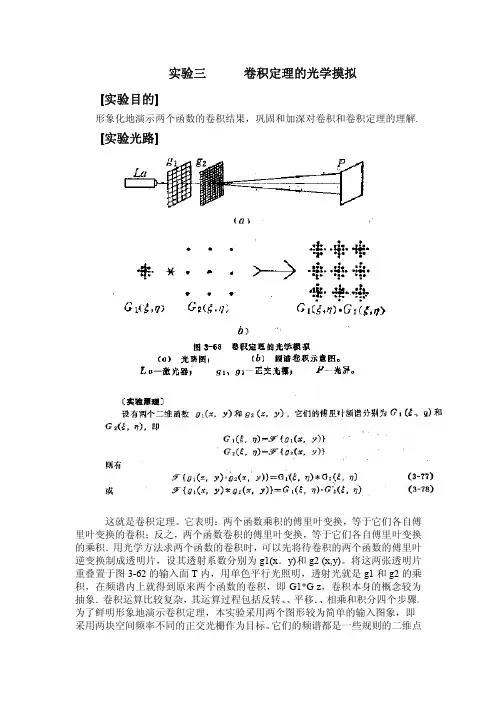
实验三卷积定理的光学摸拟[实验目的]形象化地演示两个函数的卷积结果，巩固和加深对卷积和卷积定理的理解.[实验光路]这就是卷积定理。

它表明：两个函数乘积的傅里叶变换，等于它们各自傅里叶变换的卷积；反之，两个函数卷积的傅里叶变换，等于它们各自傅里叶变换的乘积．用光学方法求两个函数的卷积时，可以先将待卷积的两个函数的傅里叶逆变换制成透明片，设其透射系数分别为g1(x．y)和g2(x,y)。

将这两张透明片重叠置于图3-62的输入面T内，用单色平行光照明，透射光就是g1和g2的乘积，在频谱内上就得到原来两个函数的卷积，即G1*G z，卷积本身的概念较为抽象．卷积运算比较复杂，其运算过程包括反转、、平移．、相乘和积分四个步骤。

为了鲜明形象地演示卷积定理，本实验采用两个图形较为简单的输入图象，即采用两块空间频率不同的正交光栅作为目标。

它们的频谱都是一些规则的二维点阵，只是空间频率高的正变光栅，其频谱分得开一些。

二者卷积的结果并不是两个图形的几何叠加，而是将一个图形反转之后加到另一个图形的每一个点上。

这样就生动地显示出卷积的过程和几何意义。

由于光栅的空间频率较高，在图3—68所示的实验光路巾采用未经扩束的激光细光束垂直照明，存足够远的屏幕上就可得到=光栅傅里叶频谱的卷积图形。

[实验步骤]1预先制作两块空间频率分别为10c／mm200c／mm的正交光栅g1和制作光路和方法参见实验3．将gi和g2分别单独置入图3—68(a)所示的光路中，观察它们的频谱G L和G z。

G1和G z都是由光点组成的二维点阵，G，的光点比较集中，G z的光点分得开一些。

2．将正交光栅g，和g2叠合在一起．用未经扩束的激光细光束垂直照明，在远处屏幕上观察卷积结果，并分别与每一块光栅各自的频谱G1和Gz作出较。

结果如图3—68(6)所示。

’3以照明激光束为轴线，旋转空间频率较低的光栅g1，观察卷积图形的变化情况。

结果是：叠加在G z图形每一个光点上的G1图形(实际上是反转的G1图形，由于Gt图形左右对称．反转后图形不变)，各自绕其中心旋转，类似地球的自转。

信息光学部分章节小结第一部分：数学基础一 几个常用函数（1）矩形函数：该二维矩形函数可用来描述无限大不透明屏上矩形孔的透过率。

（a>0,b>0）（2）sinc 函数：sin by b y a x a x b y c a x c b y a x /)/sin(/)/sin()(sin )(sin ),ππππ∙=∙= (a>0,b>0) (3)阶跃函数： （4）符号函数：（5）三角函数：二维三角函数可用来表示一个光瞳为矩形的非相干成像系统的光学传递函数 （6）高斯函数：（7）圆域函数：（8）δ函数： ⎪⎩⎪⎨⎧≤≤=∙=others b y a x by rect a x rect b y a x rect ,02,2,1)()(),(⎪⎪⎪⎩⎪⎪⎪⎨⎧>=<=0102100)(a x a x a x a x step ⎪⎪⎪⎩⎪⎪⎪⎨⎧<-=>=010001)sgn(a x a x a x a x ⎪⎩⎪⎨⎧<--=ΛΛ=Λothers b y a x b y a x b y a x b y a x ,01,),1)(1()()(),(0,]})()[(exp{),(22>+-=b a b y a x b y a x Gauss πothers r y x r r y x circ r r circ 01{)()(0220220≤+==+= 1),( 20,),( 1000000⎪⎪⎭⎪⎪⎬⎫=--︒⎩⎨⎧==∞=--︒⎰⎰∞+∞-dxdy y y x x others y y x x y y x x δδ（9）comb 函数：∑--==nm ny y mx x y x y y comb x x comb y y x x comb ,00000000),()()(),(δ 二 几种重要的数学运算1 卷积：卷积的几个重要性质： （1） 线性性质：{),(),(),(),(),()},(),(y x g y x bh y x g y x af y x g y x bh y x af *+*=*+（2） 卷积符合交换律：),(),(),(),(y x f y x h y x h y x f *=*（3） 卷积符合结合律：[][]),(),(),(),(),(),(y x g y x h y x f y x g y x h y x f **=**（4） 卷积的坐标缩放：若),(),(),(y x g y x h y x f =*，则),(1),(),(by ax g ab by ax h by ax f =* （a,b 均不等于0） （5） 卷积位移不变性：若),(),(),(),(y x f y x h y x h y x f *=*，则),(),(),(),(),(000000y y x x g y y x x h y x f y x h y y x x f --=--*=*--（6） 函数),(y x f 与δ函数的卷积：),(),(),(0000y y x x f y y x x y x f --=--*δ2 相关互相关：自相关：3 傅立叶变换 傅立叶变换对：正变换 ⎰⎰+∞∞-+-=dxdy y f x f j y x f f f F y x y x )(2exp[),(),(π 逆变换 ⎰⎰+∞∞-+=y x y x y x df df y f x f j f f F y x f )(2exp[),(),(π频谱函数),(y x f f F 一般是复函数，因此：[]),(exp ),(),(y x y x y x f f i f f F f f F φ= 傅立叶变换的重要性质：（1）线性 a,b 为任意常数ηξηξηξd d y x h f y x h y x f y x g ),(),(),(),(),(--=*=⎰+∞∞-),(),(),(),(),(y x g y x f d d y x g f y x e fg ⊗=++=⎰⎰*ηξηξηξηξηξηξηξηξηξd d f y x f d d y x f f y x f y x f y x e ff ),(),(),(),(),(),(),(**⎰⎰⎰⎰--=++=⊗=),(),(y x bg y x af +⇔(,)(,)x y x y aF f f bG f f +（2）缩放定理 （3）位移定理 [])(2ex p ),(),(b f a f i f f F b y a x f y x y x +±⇔±±π),()](2exp[),(ηξηξπ y x f f F y x i y x f ⇔+±（4）卷积定理),(),(),(),(),(),(),(),(y x y x y x y x f f G f f F y x g y x f f f G f f F y x g y x f *⇔⇔* （5）互相关定理),(),(),(),(),(),(),(),(y x y x y x y x f f G f f F y x g y x f f f G f f F y x g y x f ⊗⇔⇔⊗***由互相关定理可以推导出自相关定理。