四格表资料的Fisher确切概率法资料讲解

四格表确切概率法的应用条件
四格表确切概率法的应用条件包括：
1. 当四格表中的数据满足某一格子的理论频数T<1或者样本容量n<40时，需要使用确切概率法。

2. 当四格表中的数据满足有一个格子的理论频数1≤T<5且样本容量n≥40时，需要先进行连续性校正，然后使用确切概率法。

请注意，确切概率法是一种直接计算概率的假设检验方法，当卡方检验的应用条件不满足时，可以使用这种方法。

以上内容仅供参考，如需更专业的解释，建议咨询统计学专业人士。

fisher精确概率法的原理一、引言F i sh er精确概率法是一种常用于统计学研究中的假设检验方法。

它起源于20世纪20年代，由英国统计学家R on al dF is he r提出。

该方法主要用于小样本数据，特别是在二分类问题中，以判断某一概率值是否具有显著性差异。

本文将详细介绍Fi sh er精确概率法的原理、应用以及其在实践中的一些限制。

二、原理F i sh er精确概率法基于一个简单的原理，即对于给定的数据，存在一个或多个未知参数。

我们要基于这些数据，根据样本差异来判断这些参数的显著性是否超过某一给定的阈值。

其主要假设为样本的每一项都是独立同分布的。

三、步骤F i sh er精确概率法的步骤如下所示：1.建立零假设H0和备择假设H1：首先，我们需要明确自己的研究问题，并提出一个原始假设H0和备择假设H1。

H0通常表示无显著差异，而H1表示有显著差异。

2.计算观测值的概率：利用给定的数据，计算观测值Oc（观察到的结果）。

这个观测值是由样本数据计算得到的。

3.计算更极端结果的概率：基于零假设H0，通过计算更极端结果的概率P值，来衡量观测值O c与H0的一致性。

4.判断显著性：比较计算得到的P值与显著水平α（一般取0.05），然后根据P值是否小于α，来判断结果是否显著。

四、应用案例现在我们通过一个小案例来解释一下F ish e r精确概率法的应用：假设某药企希望判断他们新研发的药物是否能有效治疗某种疾病。

他们在30名患者身上进行了临床试验，其中20名患者服用了新药，而其他10名患者则服用了安慰剂（对照组）。

最后统计结果显示，在新药组中有16名患者病情好转，而在对照组中只有4名患者病情有所改善。

首先，我们建立零假设H0和备择假设H1。

在这个案例中，H0表示新药与安慰剂之间的治疗效果没有显著差异，H1表示新药具有显著治疗效果。

然后，我们计算观测值的概率。

根据统计结果，在新药组中16名患者病情好转，这个观测值为O c。

递进法讲解四格表fisher确切概率法
徐英;郜艳晖;李丽霞;周舒冬;李燕芬;张敏;叶小华
【期刊名称】《卫生职业教育》
【年(卷),期】2009(027)020
【摘要】教师在讲解四格表fisher确切概率法时,按照递进法的原则,遵循6个步骤,可以帮助学生充分理解其原理和方法,并进一步体会假设检验的基本过程和P值的含义.结果证明,应用该法基本可达到教学要求,可供同行借鉴.
【总页数】2页(P65-66)
【作者】徐英;郜艳晖;李丽霞;周舒冬;李燕芬;张敏;叶小华
【作者单位】广东药学院流行病与卫生统计学教研室,广东,广州,510310;广东药学院流行病与卫生统计学教研室,广东,广州,510310;广东药学院流行病与卫生统计学教研室,广东,广州,510310;广东药学院流行病与卫生统计学教研室,广东,广
州,510310;广东药学院流行病与卫生统计学教研室,广东,广州,510310;广东药学院流行病与卫生统计学教研室,广东,广州,510310;广东药学院流行病与卫生统计学教研室,广东,广州,510310
【正文语种】中文
【中图分类】G424
【相关文献】
1.四格表资料χ2检验专用公式与校正公式及确切概率法的比较
2.CASIO5x—180P（3600P）计算器在四格表的确切概率法中的应用
3.大样本四格表卡方检验
确切概率法的实现4.四格表简化直接概率法与确切概率法的关系分析5.轻型颅脑损伤的Fisher确切概率法分析
因版权原因，仅展示原文概要，查看原文内容请购买。

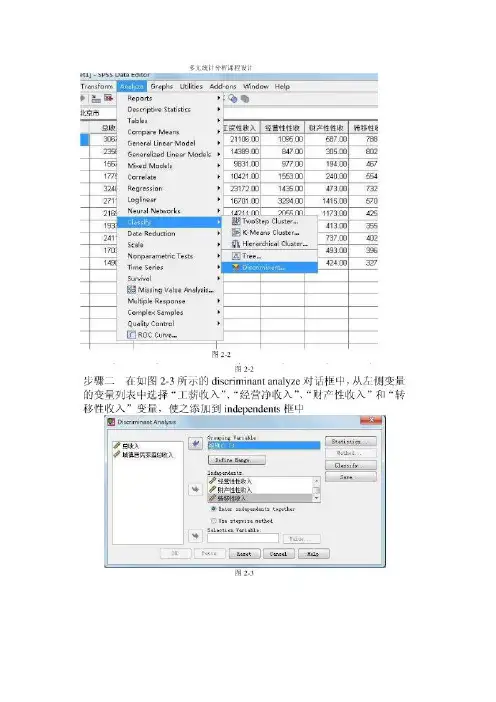
spss中怎样进行fisher精确概率法统计最短距离法是把两个类之间的距离定义为一个类中的所有案例与另一类中的所有案例之间的距离最小者.缺点是它有链接聚合的趋势,因为类与类之间的距离为所有距离中最短者,两类合并以后,它与其他类之间的距离缩小了,这样容易形成一个较大的类.所以此方法效果并不好,实际中不太用. 2.最长距离法是把类与类之间的距离定义为两类中离得最远的两个案例之间的距离.最长距离法克服了最短距离法链接聚合的缺点,两类合并后与其他类的距离是原来两个类中的距离最大者,加大了合并后的类与其他类的距离. 3.平均联结法,最短最长距离法都只用两个案例之间的距离来确定两类之间的距离,没有充分利用所有案例的信息,平均联结法把两类之间的距离定义为两类中所有案例之间距离的平均值,不再依赖于特殊点之间的距离,有把方差小的类聚到一起的趋势,效果较好,应用较广泛. 4.重心法,把两类之间的距离定义为两类重心之间的距离,每一类的重心是该类中所有案例在各个变量的均值所代表的点.与上面三种不同的是,每合并一次都要重新计算重心.重心法也较少受到特殊点的影响.重心法要求用欧氏距离,其主要缺点是在聚类过程中,不能保证合并的类之间的距离呈单调增加的趋势,也即本次合并的两类之间的距离可能小于上一次合并的两类之间的距离. 5.离差平方和法,也称沃尔德法.思想是同一类内案例的离差平方和应该较小,不同类之间案例的离差平方和应该较大.求解过程是首先使每个案例自成一类,每一步使离差平方和增加最小的两类合并为一类,直到所有的案例都归为一类为止.采用欧氏距离,它倾向于把案例数少的类聚到一起,发现规模和形状大致相同的类.此方法效果较好,使用较广.个独立样本率比较的χ2检验属四格表资料χ2检验。

这类资料在医学研究中较为多见。

例如比较两种方法治疗某种疾病的有效率是否相同？治疗结果如下：有效无效有效率（％）试验组12 1 92.31对照组 3 8 27.27可以在SPSS中进行统计分析，具体操作详见附件中的.EXE文件。

fisher确切概率法结果解读
Fisher确切概率法是一种统计学方法，主要用来尝试预测某种事件的发生概率。

通过统计抽样及计算，可以根据某种事件的特定因素来推断这类事件的后果。

Fisher确切概率法分析的变量是两个独立变量，比如身高和体重，发病率和年龄，可以通过计算其两个变量的相互关系，得到某种或某类事件发生的概率。

同时，Fisher确切概率法还提供了一种测度，用于确定不确定事件中，每个因
素发挥十分重要作用。

对一类不确定事件，把参与其中的每个因素作为一类被观察事件，通过计算每个被观察事件的发生概率来权衡每个因素所起的作用程度，以量化的形式描述出每个因素的重要性。

另外，Fisher确切概率法也用于计算某种现象发生的概率与独立发生的概率之和。

如果这种可能性接近一，就说明此现象是由它们独立地发生所造成的，也就是说，这两连续发生的现象之间没有任何关系。

总的来说，Fisher确切概率法提供了一种客观的测试，以便了解事件的发生概率以及它与其他事件之间的关系。

第三节四格表资料的Fisher确切概率法前面提及，当四格表资料中出现久，或,或用公式(8-1)与公式(8-4)计算出工值后所得的概率巴:::二时，需改用四格表资料的Fisher确切概率(Fisher probabilities in 2 x 2 table)。

该法是由R.A.Fisher(1934 年)提出的，其理论依据是超几何分布(hypergeometric distributen) ，并非工检验的范畴但由于在实际应用中常用它作为四格表资料假设检验的补充，故把此法列入本章＜下面以例8-1介绍其基本思想与检验步骤。

例8-1某医师为研究乙肝免疫球蛋白预防胎儿宫内感染HBV的效果，将33例HBsAg阳性孕妇随机分为预防注射组和非预防组，结果见表8-3。

问两组新生儿的HBV总体感染率有无差别？表8-3 两组新生儿HBV感染率的比较组别阳性阴性合计感染率(%)预防注射组 4 18 22 18.18非预防组 5 6 11 45.45合计9 24 33 27.27、基本思想在四格表周边合计数固定不变的条件下，计算表内4个实际频数变动时的各种组合之概率厂；再按检验假设用单侧或双侧的累计概率匸，依据所取的检验水准- 做出推断。

1 •各组合概率厂的计算在四格表周边合计数不变的条件下，表内4个实际频数变动的组合数共有“周边合计中最小数+1 ”个。

如例7-4，表内4个实际频数变动的组合数共有卢-1-个，依次为：(1) (2) (3) (4) (5)0 22 1 21 2 20 3 19 4 189 2 8 3 7 4 6 5 5 6ad-bc = -198 ad-bc = -165 ad-bc =：-132 ad-bc =-99 ad-bc = -66⑹(7) (8) (9) (10)5 176 167 158 149 134 7 3 8 2 9 1 10 0 11ad-bc = -33 ad-bc =0 ad-bc =33 ad-bc =66 ad-bc = 99各组合的概率'服从超几何分布，其和为1。

费舍尔确切概率法
费舍尔确切概率法是一种用于统计学中的假设检验方法。

它由英国统计学家罗纳德·费舍尔于1920年提出，是一种非参数检验方法，适用于样本量较小或数据不符合正态分布的情况。

该方法的基本思想是，通过计算样本数据的概率分布，来判断样本数据是否符合某种假设。

具体而言，费舍尔确切概率法将样本数据分成若干组，计算每组数据出现的概率，然后将这些概率相乘，得到整个样本数据出现的概率。

如果这个概率小于预先设定的显著性水平，就可以拒绝原假设。

与传统的假设检验方法相比，费舍尔确切概率法的优点在于它不需要对数据进行任何假设，也不需要对数据进行任何转换。

因此，它适用于各种类型的数据，包括分类数据、计数数据和顺序数据等。

此外，它还可以处理小样本数据，避免了小样本数据的不稳定性问题。

然而，费舍尔确切概率法也存在一些缺点。

首先，它的计算量较大，需要进行大量的计算才能得到结果。

其次，它只能处理单个假设，无法处理多个假设的情况。

最后，它对样本数据的分组方式比较敏感，不同的分组方式可能会得到不同的结果。

总的来说，费舍尔确切概率法是一种非常有用的假设检验方法，特别适用于小样本数据和非正态分布数据的情况。

在实际应用中，我们应该根据具体情况选择合适的假设检验方法，以保证结果的准确性和可靠性。

第三节四格表资料的Fisher确切概率法前面提及，当四格表资料中出现，或，或用公式(8-1)与公式(8-4)计算出值后所得的概率时，需改用四格表资料的Fisher确切概率(Fisher probabilities in 2×2 table)。

该法是由，其理论依据是超几何分布(hypergeometric distribution)，并非检验的范畴。

但由于在实际应用中常用它作为四格表资料假设检验的补充，故把此法列入本章。

下面以例8-1介绍其基本思想与检验步骤。

例8-1 某医师为研究乙肝免疫球蛋白预防胎儿宫内感染HBV的效果，将33例HBsAg阳性孕妇随机分为预防注射组和非预防组，结果见表8-3。

问两组新生儿的HBV总体感染率有无差别？表8-3两组新生儿HBV感染率的比较组别阳性阴性合计感染率（%）预防注射组 4 18 22 18.18非预防组 5 6 11 45.45合计9 24 33 27.27一、基本思想在四格表周边合计数固定不变的条件下，计算表内4个实际频数变动时的各种组合之概率；再按检验假设用单侧或双侧的累计概率，依据所取的检验水准做出推断。

1．各组合概率的计算在四格表周边合计数不变的条件下，表内4个实际频数, ,,变动的组合数共有“周边合计中最小数+1”个。

如例7-4，表内4个实际频数变动的组合数共有个，依次为：(1) (2) (3) (4) (5)0 22 1 21 2 20 3 19 4 189 2 8 3 7 4 6 5 5 6ad-bc= -198ad-bc= -165ad-bc= -132ad-bc =-99ad-bc= -66(6) (7) (8) (9) (10)5 176 167 158 149 134 7 3 8 2 9 1 10 0 11ad-bc= -33ad-bc=0ad-bc=33ad-bc=66ad-bc= 99各组合的概率服从超几何分布，其和为1。

费舍尔确切概率法费舍尔确切概率法（Fisher’s Exact Test）是一种用于分析分类数据的统计方法，它是由英国统计学家罗纳德·费舍尔（Ronald A. Fisher）于1922年提出的。

该方法是在小样本情况下进行推断的一种常用工具，特别适用于二维列联表的分析。

费舍尔确切概率法的背景和原理费舍尔确切概率法的主要应用场景是当样本量较小，无法满足传统的卡方检验条件时，例如疾病发生率的研究、临床试验数据的分析等。

传统的卡方检验在小样本情况下可能出现不准确的结果，而费舍尔确切概率法则能够准确计算出在给定边际条件下，研究结果发生的概率。

其核心原理是基于超几何分布的概率计算。

假设有一个2行2列的列联表，用来比较两个不同组别之间的差异性。

其中，行表示一个分类变量的两个水平，列表示另一个分类变量的两个水平。

计算费舍尔确切概率就是基于超几何分布计算不同条件下数据取得比观测数据更极端情况的概率。

费舍尔确切概率法的假设和计算步骤在使用费舍尔确切概率法进行分析时，需要满足以下两个假设：1.每个样本之间是独立的。

2.每个样本属于相应组别的概率是相等的。

费舍尔确切概率法的计算步骤如下：1.计算出实际观测到的列联表中各个单元格的各种不同组合方式的数量。

2.对于每种组合方式，计算该组合方式出现的概率。

这个概率是基于超几何分布计算得出的。

3.计算出观测到的列联表中极端情况出现（或更”非常”极端情况出现）的概率。

这个概率是累加观测到的列联表中所有比当前列联表更极端情况组合方式出现的概率。

4.根据2和3的概率计算出双尾或单尾的p值。

对于双尾检验的情况，将左尾和右尾的概率相加。

对于单尾检验的情况，根据研究假设选择左尾或右尾的概率。

费舍尔确切概率法的优缺点和应用领域费舍尔确切概率法的优点包括：1.在小样本情况下，能够给出准确的结果。

2.无需依赖渐近理论，适用于各种样本分布情况。

3.可应用于二维列联表的分析，适用于分类数据的比较和分析。

四格表的fisher确切概率法四格表的Fisher确切概率法是一种统计方法，用于计算两个分类变量之间的关联或相关性。

它是由英国统计学家Ronald A. Fisher在20世纪20年代提出的，并被广泛应用于医学、生物学、社会科学等领域的研究中。

Fisher确切概率法的基本思想是，通过计算观察到的数据在假设条件下出现的概率，来评估两个变量之间的关联程度。

在四格表中，横向表示一个分类变量的两个水平，纵向表示另一个分类变量的两个水平，各个单元格表示两个变量同时具有某一水平的个体数目。

首先，我们需要建立一个假设，即两个变量之间没有关联。

然后，根据该假设，计算出所有可能出现的四格表，即根据总体边际概率和个体总数，推导出每个单元格的期望频数。

接下来，计算出观察到的四格表，在给定该四格表的边际概率和个体总数的条件下出现的概率。

最后，将观察到的四格表概率与所有可能的四格表概率相比较，从而得出基于Fisher确切概率法的关联性推断。

Fisher确切概率法的优点之一是不依赖于样本大小。

无论样本规模是大还是小，该方法都能提供准确的结果。

这是因为Fisher确切概率法基于一个假设，即给定边际概率和个体总数，任何一个具体的四格表概率都是等可能的。

因此，无论样本规模如何，方法的适用性都是相同的。

另一个优点是Fisher确切概率法能够处理小样本和稀疏数据。

在实际研究中，有时候我们会遇到个体数目较少或某些单元格没有观察到的情况。

这种情况下，传统的统计方法可能会失效，而Fisher确切概率法可以通过计算所有可能的四格表概率，来获得稳健的估计。

然而，Fisher确切概率法也存在一些局限性。

首先，由于计算所有可能的四格表概率需要很大的计算量，所以在样本规模较大时，计算会变得非常耗时耗力。

此外，该方法只适用于二分类变量的关联性分析，对于多分类变量的分析则不适用。

总的来说，Fisher确切概率法是一种精确、稳健的统计方法，用于评估两个二分类变量之间的关联性。