四格表的确切概率法教学材料
- 格式:ppt
- 大小:2.09 MB
- 文档页数:30

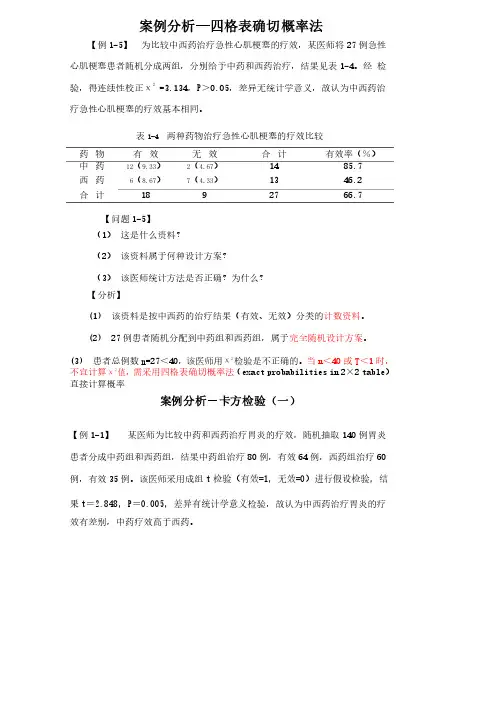
案例分析—四格表确切概率法【例1-5】为比较中西药治疗急性心肌梗塞的疗效,某医师将27例急性心肌梗塞患者随机分成两组,分别给予中药和西药治疗,结果见表1-4。
经检验,得连续性校正χ2=,P>,差异无统计学意义,故认为中西药治疗急性心肌梗塞的疗效基本相同。
表1-4 两种药物治疗急性心肌梗塞的疗效比较药物有效无效合计有效率(%)14中药12();2()西药6()7()1327合计18%9【问题1-5】(1)这是什么资料(2)该资料属于何种设计方案(3)该医师统计方法是否正确为什么【分析】(1) 该资料是按中西药的治疗结果(有效、无效)分类的计数资料。
(2) 27例患者随机分配到中药组和西药组,属于完全随机设计方案。
、(3) 患者总例数n=27<40,该医师用χ2检验是不正确的。
当n<40或T<1时,不宜计算χ2值,需采用四格表确切概率法(exact probabilities in 2×2 table)直接计算概率案例分析-卡方检验(一)【例1-1】某医师为比较中药和西药治疗胃炎的疗效,随机抽取140例胃炎患者分成中药组和西药组,结果中药组治疗80例,有效64例,西药组治疗60例,有效35例。
该医师采用成组t检验(有效=1,无效=0)进行假设检验,结果t =,P=,差异有统计学意义检验(有效=1,无效=0)进行进行假设检验,结果t=,P=,差异有统计学意义,故认为中西药治疗胃炎的疗效有差别,中药疗效高于西药。
【问题1-1】(1)这是什么资料(2)该资料属于何种设计方案(3)该医师统计方法是否正确为什么(4)该资料应该用何种统计方法【分析】 (1) 该资料是按中西药疗效(有效、无效)分类的二分类资料,即计数资料。
(2) 随机抽取140例胃炎患者分成西药组和中药组,属于完全随机设计方案。
(3) 该医师统计方法不正确。
因为成组t检验用于推断两个总体均数有无差别,适用于正态或近似正态分布的计量资料,不能用于计数资料的比较。
案例分析—四格表确切概率法【例1-5】为比较中西药治疗急性心肌梗塞的疗效,某医师将27例急性心肌梗塞患者随机分成两组,分别给予中药和西药治疗,结果见表1-4。
经检验,得连续性校正χ22=3.134,P>0.05,差异无统计学意义,故认为中西药治疗急性心肌梗塞的疗效基本相同。
表1-4两种药物治疗急性心肌梗塞的疗效比较药物有效无效合计有效率(%)中药12(9.33)2(4.67)1485.7西药6(8.67)7(4.33)1346.2合计1892766.7【问题1-5】(1)这是什么资料?(2)该资料属于何种设计方案?(3)该医师统计方法是否正确?为什么?【分析】(1)该资料是按中西药的治疗结果(有效、无效)分类的计数资料。
该资料是按中西药的治疗结果(有效、无效)分类的计数资料完全随机设计方案。
(2)27例患者随机分配到中药组和西药组,属于例患者随机分配到中药组和西药组,属于完全随机设计方案(3)患者总例数n=27<40,该医师用χ2检验是不正确的。
当n<40或T<1时,不宜计算χ2值,需采用四格表确切概率法(exact probabilities in2×2table)直接计算概率案例分析-卡方检验(一)【例1-1】某医师为比较中药和西药治疗胃炎的疗效,随机抽取140例胃炎患者分成中药组和西药组,结果中药组治疗80例,有效64例,西药组治疗60例,有效35例。
该医师采用成组t检验(有效=1,无效=0)进行假设检验,结果t=2.848,P=0.005,差异有统计学意义检验,故认为中西药治疗胃炎的疗效有差别,中药疗效高于西药。
【问题1-1】(1)这是什么资料?(2)该资料属于何种设计方案?(3)该医师统计方法是否正确?为什么?(4)该资料应该用何种统计方法?【分析】(1)该资料是按中西药疗效(有效、无效)分类的该资料是按中西药疗效(有效、无效)分类的二分类资料,即计二分类资料,即计数资料。
(2)随机抽取140例胃炎患者分成西药组和中药组,属于属于完全随机设完全随机设计方案。

南京大学学报(自然科学)第34卷 第5期 JOU RN AL OF NAN JING U NIV ERSIT Y Vol.34,No.5 1998年9月 (N ATU RAL SCIENCES ) Sept .,1998配对四格表资料差别检验的精确概率方法刘玉秀 刘 钧(南京大学医学院临床学院南京军区南京总医院 医务部,210002,南京)摘 要 探讨用于配对四格表资料差别检验的精确概率方法。
方法:在配对四格表资料两组率差为0的无效假设下,根据两项分布的原理,可导出假设检验用的精确概率计算公式,借此公式经逐一计算,给出b ≤20和c ≤10不同组合时的单、双侧检验精确概率值。
提供了配对四格表资料差别检验的精确概率计算公式,并构造出b ≤20和c ≤10的精确概率速查表。
结论:M cN emar 卡方检验方法仅适于b +c >20情形,当b +c ≤20时宜用本文介绍的精确概率方法:或通过公式计算或直接查表。
关键词 配对四格表,假设检验,精确概率分类法 R311a0 引 言医学研究中经常会遇到配对形式的四格表资料,该类资料数据处理的目的一般为推断两因素(处理)间有无关联或两处理的结果间有无差异(此种情况更为多见),前者可采用通常四格表资料处理的卡方检验法或Fisher 精确概率法,后者常规应用的方法为M cNem ar 卡方检验法,但此方法需满足一定的条件,当配对四格表中(b+c)较小(<20)时不宜使用,应考虑选用配对四格表资料差别检验的精确概率计算方法。
表1 A 、B 两种检验方法对血中某抗体的检出情况T able 1 T he o utcome o f two test matho dsA B +-合 计+461460-43640合计50501001 举 例欲比较两种检验方法对血样中某抗体的检出率,将100份血样同时用两种方法进行检测,结果为阳性或阴性。
根据检测的结果,应以血样本为基本单位,整理成数据对子数为100的配对形式的四格表资料(表1)进行两方法间检出率a收稿日期:1997-07-14;修回日期:1998-03-03第一作者简介:刘玉秀,男,1966年2月生,主治医师,现从事科研管理,曾发表“生物检定数据效价比值的广义线性模型估计”等论文差异的检验时,应进行专用于配对四格表资料的检验方法。





第三节四格表资料的Fisher确切概率法前面提及,当四格表资料中出现,或,或用公式(8-1)与公式(8-4)计算出值后所得的概率时,需改用四格表资料的Fisher确切概率(Fisher probabilities in 2×2 table)。
该法是由,其理论依据是超几何分布(hypergeometric distribution),并非检验的范畴。
但由于在实际应用中常用它作为四格表资料假设检验的补充,故把此法列入本章。
下面以例8-1介绍其基本思想与检验步骤。
例8-1 某医师为研究乙肝免疫球蛋白预防胎儿宫内感染HBV的效果,将33例HBsAg阳性孕妇随机分为预防注射组和非预防组,结果见表8-3。
问两组新生儿的HBV总体感染率有无差别?表8-3两组新生儿HBV感染率的比较组别阳性阴性合计感染率(%)预防注射组 4 18 22 18.18非预防组 5 6 11 45.45合计9 24 33 27.27一、基本思想在四格表周边合计数固定不变的条件下,计算表内4个实际频数变动时的各种组合之概率;再按检验假设用单侧或双侧的累计概率,依据所取的检验水准做出推断。
1.各组合概率的计算在四格表周边合计数不变的条件下,表内4个实际频数, ,,变动的组合数共有“周边合计中最小数+1”个。
如例7-4,表内4个实际频数变动的组合数共有个,依次为:(1) (2) (3) (4) (5)0 22 1 21 2 20 3 19 4 189 2 8 3 7 4 6 5 5 6ad-bc= -198ad-bc= -165ad-bc= -132ad-bc =-99ad-bc= -66(6) (7) (8) (9) (10)5 176 167 158 149 134 7 3 8 2 9 1 10 0 11ad-bc= -33ad-bc=0ad-bc=33ad-bc=66ad-bc= 99各组合的概率服从超几何分布,其和为1。

案例分析—四格表确切概率法【例1-5】为比较中西药治疗急性心肌梗塞的疗效,某医师将27例急性心肌梗塞患者随机分成两组,分别给予中药和西药治疗,结果见表1-4。
经检验,得连续性校正χ2=3.134,P>0.05,差异无统计学意义,故认为中西药治疗急性心肌梗塞的疗效基本相同。
表1-4 两种药物治疗急性心肌梗塞的疗效比较药物有效无效合计有效率(%)中药12(9.33)2(4.67)1485.7西药 6(8.67)7(4.33)1346.2合计1892766.7【问题1-5】(1)这是什么资料?(2)该资料属于何种设计方案?(3)该医师统计方法是否正确?为什么?【分析】(1) 该资料是按中西药的治疗结果(有效、无效)分类的计数资料。
(2) 27例患者随机分配到中药组和西药组,属于完全随机设计方案。
(3) 患者总例数n=27<40,该医师用χ2检验是不正确的。
当n<40或T<1时,不宜计算χ2值,需采用四格表确切概率法(exact probabilities in 2×2 table)直接计算概率案例分析-卡方检验(一)【例1-1】某医师为比较中药和西药治疗胃炎的疗效,随机抽取140例胃炎患者分成中药组和西药组,结果中药组治疗80例,有效64例,西药组治疗60例,有效35例。
该医师采用成组t检验(有效=1,无效=0)进行假设检验,结果t=2.848,P=0.005,差异有统计学意义检验(有效=1,无效=0)进行进行假设检验,结果t=2.848,P=0.005,差异有统计学意义,故认为中西药治疗胃炎的疗效有差别,中药疗效高于西药。
【问题1-1】(1)这是什么资料?(2)该资料属于何种设计方案?(3)该医师统计方法是否正确?为什么?(4)该资料应该用何种统计方法?【分析】(1) 该资料是按中西药疗效(有效、无效)分类的二分类资料,即计数资料。
(2) 随机抽取140例胃炎患者分成西药组和中药组,属于完全随机设计方案。


案例分析-四格表确切概率法【例1—5】为比较中西药治疗急性心肌梗塞的疗效,某医师将27例急性心肌梗塞患者随机分成两组,分别给予中药和西药治疗,结果见表1-4。
经检验,得连续性校正χ2=3。
134,P>0。
05,差异无统计学意义,故认为中西药治疗急性心肌梗塞的疗效基本相同.表1-4 两种药物治疗急性心肌梗塞的疗效比较药物有效无效合计有效率(%)中药12(9.33)2(4.67)1485。
7西药 6(8。
67)7(4。
33)1346。
2合计1892766。
7【问题1—5】(1)这是什么资料?(2)该资料属于何种设计方案?(3)该医师统计方法是否正确?为什么?【分析】(1) 该资料是按中西药的治疗结果(有效、无效)分类的计数资料。
(2) 27例患者随机分配到中药组和西药组,属于完全随机设计方案. (3)患者总例数n=27<40,该医师用χ2检验是不正确的。
当n<40或T<1时,不宜计算χ2值,需采用四格表确切概率法(exact probabilities in 2×2 table)直接计算概率案例分析-卡方检验(一)【例1—1】某医师为比较中药和西药治疗胃炎的疗效,随机抽取140例胃炎患者分成中药组和西药组,结果中药组治疗80例,有效64例,西药组治疗60例,有效35例。
该医师采用成组t检验(有效=1,无效=0)进行假设检验,结果t=2.848,P=0.005,差异有统计学意义检验(有效=1,无效=0)进行进行假设检验,结果t=2。
848,P=0。
005,差异有统计学意义,故认为中西药治疗胃炎的疗效有差别,中药疗效高于西药。
【问题1—1】(1)这是什么资料?(2)该资料属于何种设计方案?(3)该医师统计方法是否正确?为什么?(4)该资料应该用何种统计方法? 【分析】(1)该资料是按中西药疗效(有效、无效)分类的二分类资料,即计数资料。
(2)随机抽取140例胃炎患者分成西药组和中药组,属于完全随机设计方案.(3) 该医师统计方法不正确.因为成组t检验用于推断两个总体均数有无差别,适用于正态或近似正态分布的计量资料,不能用于计数资料的比较。
Excel⽤于Fisher确切概率法(⼀)Excel⽤于Fisher确切概率法(⼀)【摘要】给出⽤Excel电⼦表格计算确切概率的⽅法。
【关键词】Excel电⼦表格;确切概率法;实际频数与理论频数在医药试验中常常进⾏病例对照研究,⽤以检验对照组和处理组之间是否有显著性异,这类问题的原始数据如果属于计数资料,可以将资料整理成如下四格表。
表1四格表组别具有某种特征不具有某种特征合计对照组aba+b处理组cdc+d合计a+cb+da+b+c+d在统计处理上,根据样本容量n(n=a+b+c+d)的⼤⼩选取统计⽅法3]:①当样本容量n>40,且理论频数T>5时,⽤χ2检验;②当n>40,但1 1Fisher确切概率法其检验步骤如下3]:①先计算四格表的实际频数T0=|ad-bc|/n;②保持表1的第4⾏和第4列的合计值不变,让四格表中的数据发⽣变化,得到⼀系列四格表;③按T0的公式计算每个四格表的实际频数与理论频数之差的绝对值作为Ti;④计算Ti≥T0对应的四格表发⽣的概率:Pi=(a+b)!(a+c)!(d+b)!/ai!bi!ci!di!n!⑤令⑥由P的⼤⼩做出推断。
2Excel电⼦表格⽤于确切概率法的操作下⾯⽤具体的实例介绍其操作步例1在某牧区观察慢性布鲁⽒病患者植物⾎凝素(PHA)⽪肤试验反应,资料如下表2,问活动型与稳定型患者PHA反映阳性率有⽆差异1]?表2两型慢性布鲁⽒病的PHA⽪试反应病⼈分型阳性数阴性数合计活动型11415稳定型3710合计42125①打开Excel新建⼀个电⼦表格。
②计算T0在A1中输⼊T0=,在B1中输⼊=ABS(1*7-3*14)/25,回车。
B1中显⽰结果为1.4,这⾥ABS表⽰绝对值。
第五讲 四格表及单侧给定时的检验一、引例例 选择63个肺癌病例,选择43个与肺癌患者年龄、性别和其它属性相类似的健康人作为对照组。
然后分别调查肺癌患者和对照组中的人的吸烟情况。
调查结果如表1。
表1 调查结果调查结果算得肺癌患者中吸烟的比率为60/63=95.2%,对照组中吸烟的比例为32/43=74.4%。
问总体中肺癌患者吸烟的比例是否比健康人吸烟的比例高?二、四格表 1、记号11n 表示既有属性A ,又有属性B 的个体数;12n 表示有属性A ,但没有属性B 的个体数; 21n 表示没有属性A ,但有属性B 的个体数; 22n 表示既没有属性A ,又没有属性B 的个体数; 11112n n n +=+表示具有属性A 的个体数;22122n n n +=+表示不具有属性A 的个体数;11121n n n +=+表示具有属性B 的个体数; 21222n n n +=+表示不具有属性B 的个体数;111221221212n n n n n n n n n ++++=+++=+=+表示总的个体数。
2、四格表表2 四格表及其边际3、四格表的抽样方式四格表的边际有1212,,,,n n n n n ++++五个数,按边际是否给定有如下四种不同的抽样方式:(1)单侧给定,如给定12,n n ++,11122122,,,n n n n 中只有两个如1121,n n 是随机变量,它们相互独立。
11121121112122222221n n n n n n n n n n n n +++++==-⎧⎧⇒⎨⎨+==-⎩⎩ 方程组有两个独立的自由未知量。
(2)样本容量n 给定,11122122,,,n n n n 中有三个如111221,,n n n 是随机变量,它们相互独立。
1112212222111221n n n n n n n n n n +++=⇒=---方程组有三个独立的自由未知量。
(3)1212,,,,n n n n n ++++都没有给定,即完全随机时,11122122,,,n n n n 都是随机变量,它们相互独立。