当前位置：文档之家 › 四格表分析

四格表分析

  • 格式：ppt
  • 大小：3.30 MB
  • 文档页数：28

下载文档原格式

  / 28

合集下载

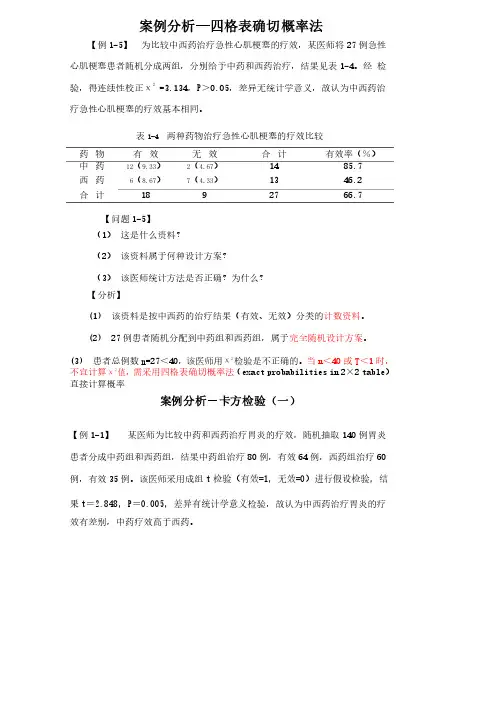
医学统计学案例分析2

医学统计学案例分析2

案例分析—四格表确切概率法【例1-5】为比较中西药治疗急性心肌梗塞的疗效，某医师将27例急性心肌梗塞患者随机分成两组，分别给予中药和西药治疗，结果见表1-4。

经检验，得连续性校正χ22=3.134，P＞0.05，差异无统计学意义，故认为中西药治疗急性心肌梗塞的疗效基本相同。

表1-4两种药物治疗急性心肌梗塞的疗效比较药物有效无效合计有效率（％）中药12（9.33）2（4.67）1485.7西药6（8.67）7（4.33）1346.2合计1892766.7【问题1-5】（1）这是什么资料？（2）该资料属于何种设计方案？（3）该医师统计方法是否正确？为什么？【分析】(1)该资料是按中西药的治疗结果（有效、无效）分类的计数资料。

该资料是按中西药的治疗结果（有效、无效）分类的计数资料完全随机设计方案。

(2)27例患者随机分配到中药组和西药组，属于例患者随机分配到中药组和西药组，属于完全随机设计方案(3)患者总例数n=27＜40，该医师用χ2检验是不正确的。

当n＜40或T＜1时，不宜计算χ2值，需采用四格表确切概率法（exact probabilities in2×2table）直接计算概率案例分析－卡方检验（一）【例1-1】某医师为比较中药和西药治疗胃炎的疗效，随机抽取140例胃炎患者分成中药组和西药组，结果中药组治疗80例，有效64例，西药组治疗60例，有效35例。

该医师采用成组t检验（有效=1，无效=0）进行假设检验，结果t＝2.848，P＝0.005，差异有统计学意义检验，故认为中西药治疗胃炎的疗效有差别，中药疗效高于西药。

【问题1-1】（1）这是什么资料？（2）该资料属于何种设计方案？（3）该医师统计方法是否正确？为什么？（4）该资料应该用何种统计方法？【分析】(1)该资料是按中西药疗效（有效、无效）分类的该资料是按中西药疗效（有效、无效）分类的二分类资料，即计二分类资料，即计数资料。

(2)随机抽取140例胃炎患者分成西药组和中药组，属于属于完全随机设完全随机设计方案。

四格表资料的χ2检验生存率

四格表资料的χ2检验生存率

四格表资料的χ2检验生存率四格表资料的卡方检验是一种用于比较观察值与期望值之间差异的统计方法。

在生存率研究中，卡方检验可以用来比较两个或多个组群在不同条件下的生存情况，以确定是否存在显著差异。

卡方检验是基于观察值与期望值之间的差异来进行的。

在生存率研究中，我们通常会将样本人群分为不同的组群，根据他们的特征或接受的治疗方式等因素。

然后我们会观察每个组群中生存和死亡的人数，并计算出每个组群中期望的生存和死亡人数。

卡方检验的原假设是组群之间没有显著差异，即观察值和期望值之间的差异是由于随机性引起的。

如果计算出的卡方值足够小，就可以拒绝原假设，得出结论认为组群之间存在显著差异，即生存率之间存在显著差异。

在进行卡方检验时，首先需要定义显著性水平，通常我们选择0.05作为显著性水平。

接下来，需要计算观察值与期望值之间的差异。

差异可以用卡方检验的统计量来计算，该统计量的公式如下：χ2 = ∑ [(Oij - Eij)² / Eij]其中，Oij表示观察到的频数，Eij表示期望的频数。

计算完卡方值后，需要查找卡方分布表来确定对应的p值，p值是指在原假设成立的情况下，观察到的卡方值更极端的概率。

如果p值小于显著性水平0.05，则可以拒绝原假设，得出结论认为组群之间存在显著差异。

如果p值大于0.05，则不能拒绝原假设，即认为组群之间没有显著差异。

在实际应用中，我们需要根据具体的研究目的和数据情况来选择适当的四格表和实施卡方检验。

举例来说，我们可以比较两种不同治疗方式对癌症患者的生存率是否有影响。

我们可以将患者分为两个组群，一组接受A治疗，另一组接受B治疗。

然后观察每个组群中生存和死亡的人数，并计算出期望的生存和死亡人数。

最后，使用卡方检验来比较两个组群的生存情况。

卡方检验的优点是：可以应用于多种情况下的数据分析，适用于比较样本数据与理论预期之间的差异；计算方法相对简单，不需要任何参数估计；可以得到一个明确的结果，即接受或拒绝原假设。

医学统计学案例分析 2

医学统计学案例分析 2
别，甲法测定阳性率较高。
表 1-3 两种方法测定结果比较
测定方法 甲法 乙法 合计
阳性数 42 23 65
阴性数 18 37 55
合计 60 60
120
阳性率（%） 70.0 38.3 54.2
【问题 1-4】（1）这是什么资料？（2）该资料属于何种设计方案？
（3）该医师统计方法是否正确？为什么？（4）该资料应采用何种统计方法？ 【分析】(1) 该资料是按两种方法测定结果（阳性、阴性）二分类的计数资料。 (2) 该设计为同一受试对象接受两种不同的处理，属于自身配对设计方案。(3)
【分析】 (1) 该资料是随机抽取当地 30 名小学男生和女生作为样本，测定每个 观察对象的卡介苗抗体滴度，属于完全随机设计。 (2) 由于抗体滴度值是等比 资料，服从对数正态分布, 各组的平均滴度应用几何均数（G）描述，其假设检 验不能直接用完全随机设计两样本均数比较的 t 检验, 而应将观察值进行对数 变换后再用 t 检验。
步骤如下：
1．建立检验假设，确定检验水准 H0：两药的有效率相等，即 π1＝π2 H1：两药的有效率不等，即π1≠π2
2．计算检验统计量 值 (1) 计算理论频数 根据公式 计算理论频数，填入表 7-2 的括号内。 (2) 计算χ2 值
具体计算略。
3．确定 P 值，做出统计推断
查附表
6（χ2
2
界值表），X 0.05,1=3.84
分组
尿中类固醇排出量（mg/dl）
正 常 人 2.90 5.41 5.48 4.60 4.03 5.10 4.97 4.24 4.37 3.05 2.78
脑病病人 5.28 8.79 3.84 6.46 3.79 6.64 5.89 4.57 7.71 6.02 4.06

完全随机设计四格表资料的卡方检验,其校正公式

完全随机设计四格表资料的卡方检验,其校正公式

完全随机设计四格表资料的卡方检验,其校正公式完全随机设计四格表资料的卡方检验及校正公式 卡方检验是一种常用的统计方法，用于判断两个或多个分类变量之间是否存在关联性。

在实际应用中，有一类叫做四格表的数据分析问题，即由两个分类变量构成的表格。

本文将介绍如何进行完全随机设计四格表资料的卡方检验，并给出相应的校正公式。

一、完全随机设计四格表资料的卡方检验的步骤：1. 确定研究问题和假设： 在进行卡方检验之前，需要明确研究问题和研究假设。

例如，我们想知道两个分类变量X和Y是否存在关联性，即是否存在某种程度的相关关系。

2. 构建四格表： 根据研究问题，我们需要构建一个四格表来表示变量X和Y的关系。

四格表由两个分类变量构成，每个变量有两个水平。

研究中可以将观察单位按照两个变量进行分类，并统计每个分类组合的数量。

将这些数量填入四格表格中，得到以下形式：Y=1 Y=03. 计算期望频数： 在进行卡方检验时，需要计算期望频数，即在假设不存在关联性的情况下，每个格子的期望数量。

计算方法为：在保持边际分布不变的条件下，计算每个格子的期望频数。

即计算每个分类组合的边际比例乘以总体数量。

4. 计算卡方统计量： 卡方统计量用于判断观察频数和期望频数之间的差异。

计算方法为：将每个格子的观察频数与期望频数之差的平方，除以期望频数，然后将所有格子的结果相加。

得到的卡方统计量符合自由度为1的卡方分布。

5. 判断是否存在关联性： 根据卡方统计量的分布，可以计算出其对应的p值。

通过比较p值和显著性水平（通常为0.05），可以判断是否存在关联性。

若p 值小于显著性水平，即拒绝原假设，说明存在关联性。

二、校正公式： 在实际应用中，四格表可能会出现某个格子的期望频数小于5的情况。

这会导致卡方统计量的计算结果不准确，影响判断结果的可靠性。

为了解决这个问题，可以使用校正公式进行修正。

1. 构建校正后的四格表： 在校正前，首先需要确定哪些格子的期望频数小于5。

四格表（1）：Pearson卡方检验

四格表（1）：Pearson卡方检验
业人员看来很简单的统计方法的学习还是非常迫切。因
此，计划从四格表开始，为大家逐日介绍一系列的扫盲文章。 师姐的名言是“对于统计我已经放弃治疗了。”衷心希望她看完这篇文章后要积极“治疗”。 以下源自H师姐论文的实例。 基本概念
定性资料定性资料是指分析的资料中，结果变量的性质是定性的。定性资料又可细分为名
况如下表，试比较两组胎儿分娩方式中剖宫产率有无差别。 1建立数据文件 2数据加权 3交叉表分析 结果解释1 观察组的剖宫产率为50%，对照组的剖宫产率为33.9%。 结果解释2 由于总例数n=173＞40，四个格内没有＜5的理论频数（期望计数），因此我们应读取第一 行的皮尔逊卡方值（6.002），P=0.01＜0.05。按α=0.05水准，可认为两组的剖宫产率的差别有 统计学意义，即观察组的剖宫产率高于对照组。 注：有 观 点 认 为 在 四 格 表 中 采 用 Fisher精 确 检 验 的 结 果 比 较 可 靠 ， 对 于 统 计 软 件 计 算 的 结 果 ， 四 格 表 均 可 采 用 Fisher精 确 检 验 的 结 果 ， 本例P=0.022＜0.05，和上述结果是一致 的。
义资料和有序资料，对于每一个具体的观察单位或个体来说，若观测的指标是定性的，其表现 形式通常不是真实的数据，而只是一个“名称或符号”。名义资料从每个受试对象身上观察的结果 不是一个具体数值，而是一种状态或名称，如某病患者治疗的结果为“治愈”或“未治愈”；检测结 果为“阴性”或“阳性”、职业为“工人”、“农民”或“医生”等。例题某医院对门诊产前检查并住院分娩 的孕36~41周无其他高危因素的孕妇为研究对象中，出现规则变化脐动脉血流频谱曲线的孕晚期 胎儿为观察组，出现正常脐动脉血流频谱的孕晚期胎儿为对照组。两组胎儿的分娩方式情况情

四格表卡方检验

四格表卡方检验

发病率 (0/00) =④/② 1.61
1.93
死亡率 (0率 （%） =⑤/③ 2.60
5.51
55~
65~
36584
10343
214
95
125
87 479
15
23 61
20.11
8.93
5.85
9.18
3.42
8.41 2.39
0.41
2.22 0.30
7.94
英国统计学家
1901年10月与 Weldon，Galton 一起创办 Biometvika
2019年3月28日
例8-1 某医院收治376例胃脘痛患者，随机分 为两组，分别用新研制的中药胃金丹和西药治疗。 结果如表8-1，探讨两药疗效有无差别。
表8-1 疗法 胃金丹 西药 合 计 两药治疗胃脘痛的疗效四格表 有效 271(253.24) 74(91.76) 345 无效 5(22.76) 26(8.24) 31 合计 276 100 376 有效率 98.19% 74.00% 91.76%

2019年3月28日
理论数公式
nr nc Trc ，nr 表示第r行的合计数； n nc 表示第c列的合计数； n表示总合计。
271
5
253.24 22.76 91.76 8.24
74
26
2019年3月28日
衡量理论数与实际数的差别
检验统计量
R ,C
2 值：
2 2 ( A T ) （ A T ） 2 rc rc Trc T r ,c 1
第一节
常用相对数
医药统计中的资料类型
常用相对数指标
应用注意事项

四格表卡方检验


四格表确切概率法的基本思想
在四格表周边合计固定不变的条件下，改 变某一格子的实际频数，列出a、b、c、d各种 组合的四格表，按公式8-9计算每个四格表的概 率，然后计算单侧或双侧累积概率，并与检验 水准α比较，作出是否拒绝H0的结论。
P （a b)!(c d )!(a c)!(b d )! a! b! c! d ! n!
第13页/共42页
例8-1 用专用公式 计算 2 值：
2 (271 26 5 74)2 376 56.77 , df 1
276100 345 31
查
2界
值
表
，
2 0.05,1
3.84
下结论：
2
2 0.05,1
3.84;
P 0.05，按 0.05水准，
拒
绝H
，
0
接
受H
，
1
可
以
认
为
疗
效
四格表确切概率法系英国统计学家fisher于1934年提出又称fisher精切概率法fiserexacttest在四格表周边合计固定不变的条件下改变某一格子的实际频数列出abcd各种组合的四格表按公式89计算每个四格表的概率然后计算单侧或双侧累积概率并与检验水准比较作出是否拒绝h组别改善无效合计红花散1520安慰剂1417181937例83研究中药制剂红花散改善周围血管闭塞性病变患者的皮肤微循环状况以安慰剂作对照将37个病例随机分到两组结果如表85分析红花散的疗效
第6页/共42页
一、卡方检验的基本思想
例8-1 对表8-1资料推断两药的疗效有无差别
H0:
1
，即两药总体有效率相等
2
由于总体有效率未知，将两组数据合并，计算合并

四格表分析


2 P
k i 1
( Ai
Ti )2 Ti
服从自由度为k-1旳卡方分布。
即：
2 P
2,v，拒绝H0。
上述卡方检验由此派生了不同应用背景旳多种问 题旳检验，尤其最常用旳是两个样本率旳检验等。
措施原理
牙膏类型 含氟牙膏 一般牙膏 合计
表 6.2 使用含氟牙膏与一般牙膏儿童的龋患率
患龋齿人数 70(76.67) 45(38.33) 115
此时,能够考虑边际卡方检验，见P130
注意事项
配对四格表卡方与成组设计卡方
因为配对设计旳资料同一对观察成果间一般是非独 立旳，而成组设计旳资料一般能够以为是独立旳， 所以配对四格表资料不能用成组设计旳2或 Fisher检验旳，而要用配对设计旳2或配对设计 旳直接计算概率法进行检验。
Poisson分布资料推断
累计概率 0.0106 0.0895 0.3138 0.6306 0.8726 0.9745 0.9974 0.9999 1.0000
*本例现有样本情况 d=6。
❖ 然后将其中不大于等于既有样本概率旳概率值相加，即为
P值：
▪ 本例中P值=P(0)+ P(6)+P(7)+P(8)=0.0361<0.05
措施原理
❖ 理论频数
▪ 基于H0成立，两样本所在总体无差别旳前提下
计算出各单元格旳理论频数来
TRC
nR nC n
牙膏类型 含氟牙膏 一般牙膏 合计
患龋齿人数 70(76.67) 45(38.33) 115
未患龋齿人数 130(123.33) 55(61.67) 185
调查人数 200 100 300
❖ 使用不同旳牙膏并不会影响龋齿旳发生（两个分 类变量间无关联） ▪ 两变量旳有关分析

四格表卡方检验

自由度的确定
通常为分类数减去1
理论次数的计算
根据某种经验或理论
二、配合度检验的应用
1、检验无差假说 理论次数=总数*1/分类项数 例题p.332
2、检验假设分布的概率 理论次数的计算按照理论分布求得 例题p.333
三、连续变量分布的吻合性检验
对于连续随机变量的计量数据，有时在 实际研究中预先不知道其总体分布，而 是要根据对样本的次数分布来判断是否 服从某种指定的具有明确表达式的理论 次数分布。 关于分布的假设检验方法有很多，运用 卡方值所做的配合度检验是最常用的一 种。
举例：正态分布吻合性检验
例题：p.336
四、比率或百分数的配合度检验
如果计数资料用百分数表示，最后计算 出来的卡方值要乘以100/N后，再与查表 所得的临界值进行比较。 例题：p.337
五、二项分类的配合度检验与比 率显著性检验的一致性
二者实质相同，只是表示方式不同。 相比较而言，配合度检验计算方法更为 简单。
在独立性检验和同质性检验中，如果两 个变量或两个样本无关联时，期望值为 列联表中各单元格的理论次数，即各个 单元格对应的两个边缘次数的积除以总 次数。
五、小期望次数的连续性校正
如果个别单元格的理论次数小于5，处理 方法有以下四种：
1、单元格合并法 2、增加样本数 3、去除样本法 4、使用校正公式
主要内容
第一节 卡方检验的原理 第二节 配合度检验 第三节 独立性检验 第四节 同质性检验
为什么叫作卡方检验
计数数据一般应用属性统计方法，因为 这类数据是按照事物属性进行多项分类 的。 而且，对这些计数数据的统计分析是根 据卡方分布进行的。
卡方检验的功能
处理一个因素两项或多项分类的实际观 察频数与理论频数分布是否相一致的问 题，或者说有无显著差异的问题。

计数资料的数据分析

计数资料的数据分析1、四格表资料（1）简单四格表资料i.非配对的四格表资料例：比较A、B两种疗法治愈率，数据如下:分析目的：A、B疗法有效率是否有差异？数据如用通用符号表示：分析方法：Pearson 卡方检验其中，Oi 表示观察数，Ei表示理论期望数， n 格子数（这里等于4）Yates'连续性校正关联分析：计算A疗法有效率相对于B疗法的优势比Odds Ratio （比值比）= (a/b) / (b/d) = (ad)/(bc) = (20*14)/(16*10) = 1.75易侕统计软件输入界面：易侕统计软件输出结果：ii. 配对的四格表资料例：比较A、B两种疗法治愈率，配对设计，每个病人与另一个年龄、性别、病程等相同的病人配对，一个用 A疗法治疗，另一个病人用B疗法治疗，数据如下分析目的：A、B疗法有效率是否有差异？： H0：A、B疗法有效率相同，即p b=p c数据如用通用符号表示：McNemar 卡方检验Edwards 连续性校正：McNemar精确检验：总共有b+c （8+4=12）不一致的对子数，按H0，理论上b与c出现的概率相同，即b占（b+c）的比例为50%，相当于OR=b/c=1。

实际观察到的OR = b/c = 8/4 =2，计算出现8/4 或更极端的情况（9/3，10/2，11/1，12/0）的概率。

易侕统计软件输入界面：易侕统计软件输出结果：McNemar 配对四格表卡方检验（2）诊断试验四格表资料分析目的：分析试验结果与真实情况（金标准）的吻合程度。

金标准是指当前公认的诊断疾病最可靠的标准方法，可正确区分“有病”或“无病”。

数据如用通用符号表示：分析指标：1. 检测患病率(prevalence)是指被检测的全部对象中，检测出来的患者的比例。

即：检测患病率 = (a+b)/(a+b+c+d)2. 实际患病率(prevalence)是指被检测的全部对象中，真正患者的比例。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。


2 P

k i1
( Ai
Ti )2 Ti
服从自由度为k-1的卡方分布。
即：P2 2,v，拒绝H0。
上述卡方检验由此派生了不同应用背景的各种问 题的检验，特别最常用的是两个样本率的检验等。
方法原理
牙膏类型 含氟牙膏 一般牙膏 合计
表 6.2 使用含氟牙膏与一般牙膏儿童的龋患率
患龋齿人数 70(76.67) 45(38.33) 115
此时,可以考虑边际卡方检验，见P130
注意事项
配对四格表卡方与成组设计卡方
由于配对设计的资料同一对观察结果间一般是非独 立的，而成组设计的资料一般可以认为是独立的， 所以配对四格表资料不能用成组设计的2或 Fisher检验的，而要用配对设计的2或配对设计 的直接计算概率法进行检验。
Poisson分布资料推断
注意事项
❖ McNemar检验(配对卡方检验)只会利用非主对角线 单元格上的信息，即它只关心两者不一致的评价 情况，用于比较两个评价者间存在怎样的倾向。 因此，对于一致性较好的大样本数据(a,d较大且 b,c较小时)，McNemar检验可能会失去实用价值。 ▪ 例如对1万个案例进行一致性评价，9995个都是 完全一致的，在主对角线上，另有5个分布在左 下的三角区，显然，此时一致性相当的好。但 如果使用McNemar检验，此时反而会得出两种评 价有差异的结论来。
▪ H0：行分类变量与列分类变量无关联
▪ H1：行分类变量与列分类变量有关联
▪ =0.05
▪ 统计量
P2

k i1
( Ai
Ti )2 Ti
，其中Ai是样本资料的
计 数 ， Ti 是 在 H0 为 真 的 情 况 下 的 理 论 数 ( 期 望
值)。
卡方检验
▪ 在H0为真时，实际观察数与理论数之差Ai－Ti 应该比较接近0。所以在H0为真时，检验统计量
76.67
123 .33
38.33
61.67
2.82
操作步骤
4. 确定P值和作出推断结论 ▪ 查附表8，2界值表，得p>0.05。按 = 0.05 水准，不拒绝H0，尚不能认为使用含氟牙膏比
使用一般牙膏儿童的龋患率低。 ▪ 对于四格表，卡方的计算公式又可进行简化，
以方便手工计算
卡方检验假设的等价性
未患龋齿人数 130(123.33) 55(61.67)
185
调查人数 200 100 300
龋患率（%） 35.00 45.00 38.33
更一般地，可将上述表格记为表 6.3 的一般形式，称之为四格表(fourfold table)。因为表 中 a、b、c 和 d 四个格子的数据是基本的，其余数据均可从这四个数据派生出来。
P (a b)!(c d )!(a c)!(b d)! a!b!c!d!n!
方法原理
表 6.10 在四格表(表 6.9)周边合计不变的条件下，1=2 时的概率分布计算
d
0
1
2
3

5
6*
7
8
P(d) 0.0106 0.0789 0.2244 0.3168 0.2420 0.1019 0.0229 0.0025 0.0001
龋患率（%） 35.00 45.00 38.33
方法原理
• 从卡方的计算公式可见，当观察频数与期望频数完全 一致时，卡方值为0；
• 观察频数与期望频数越接近，两者之间的差异越小， 卡方值越小；
• 反之，观察频数与期望频数差别越大，两者之间的差 异越大，卡方值越大。
• 当然，卡方值的大小也和自由度有关。
❖ 两组儿童的龋齿率相同 ▪ 两组发生率的比较
❖ 使用不同的牙膏并不会影响龋齿的发生（两个分 类变量间无关联） ▪ 两变量的相关分析
四格表2值的校正
❖ 英国统计学家Yates认为，2分布是一种连续型分 布，而四格表资料是分类资料，属离散型分布， 由此计算的2值的抽样分布也应当是不连续的， 当样本量较小时，两者间的差异不可忽略，应进 行连续性校正（在每个单元格的残差中都减去0.5）
累计概率 0.0106 0.0895 0.3138 0.6306 0.8726 0.9745 0.9974 0.9999 1.0000
*本例现有样本情况 d=6。
❖ 然后将其中小于等于现有样本概率的概率值相加，即为P
值：
▪ 本例中P值=P(0)+ P(6)+P(7)+P(8)=0.0361<0.05
表 6.9，问新药疗效与对照组疗效有无差别？
表 6.9 某新药治疗原发性高血压的疗效
分组
有效
无效
合计
有效率（）
试验组
20(a)
8(b)
28
71.43
对照组
2(c)
6(d)
8
25.00
合计
22
14
36
61.11
分析实例
1．建立检验假设和确立检验水准
▪ H0：新药组与对照组疗效相等，即 1 = 2 ▪ H1：新药组与对照组疗效不等，即 1 2
一点补充
❖ 确切概率法可以考虑单边检验 ❖ 对于较大的行乘列表，确切概率法的计算量将变
得十分惊人，有可能超出硬件系统可以支持的范 围
配对设计两样本率比较的 χ2检验
方法原理
例6.9 用A、B两种方法检查已确诊的乳腺癌患者 140名，A法检出91名(65%)，B法检出77名(55%)， A、B两法一致的检出56名(40%)，问哪种方法阳性 检出率更高？
▪ 若n > 40 ，此时有 1< T 5时，需计算Yates
连续性校正2值
▪ T <1，或n<40时，应改用Fisher确切概率法直
接计算概率
确切概率法
分析实例
▪ 注意：确切概率法不属于2检验的范畴，但常 作为2检验应用上的补充。
例 6.13 研究某新药治疗原发性高血压的疗效，并用常规治疗药物作为对照组，结果见
A法
＋ － 合计
＋ 56 (a) 21 (c) 77
B法 －
35 (b) 28 (d) 63
合计
91 49 140
方法原理
• 显然，本例对同一个个体有两次不同的测量，从 设计的角度上讲可以被理解为自身配对设计
• 上述问题为：两种“处理”之差别分析
方法原理
❖ 注意 ▪ 考虑该例四格表中两处理阳性检出率是否相同 只要考虑四格表中的非对角元素的差异
方法原理
❖ 理论频数
▪ 基于H0成立，两样本所在总体无差别的前提下
计算出各单元格的理论频数来
TRC

nR nC n
牙膏类型 含氟牙膏 一般牙膏 合计
患龋齿人数 70(76.67) 45(38.33) 115
未患龋齿人数 130(123.33) 55(61.67) 185
调查人数 200 100 300
chi-square
操作步骤
1. 建立检验假设和确定检验水准
▪ H0：使用含氟牙膏和一般牙膏儿童龋患率相等 ▪ H1：使用含氟牙膏和一般牙膏儿童龋患率不等 2. =0.05 3.计算检验统计量2值
2 70 76.67 2 130 123 .332 45 38.332 55 61.67 2
❖ Poisson分布资料是离散型资料，但不具有分类特征，故 视为计量资料。
❖ Poisson分布两样本来自总体均数是否相等的比较 ❖ 1.两样本观察单位相同：在每个样本的观察值大于20时，
基于正态近似可以构造两样本总体均数的检验。 ❖ 2.两样本观察单位不等：应将观察计数化为观察单位相同
的平均水平，再基于正态近似构造两样本总体均数的检验
四格表资料分析 卡方检验
以及Poisson资料分析
内容
1
四个表和卡方检验原理
2 成组设计两样本率比较的卡方检验
3
确切概率法
4 配对设计两样本率比较的卡方检验
5
Poisson资料分析
卡方检验入门
概述
❖ 卡方检验是以卡方分布为基础的一种常用假设检 验方法，主要用于分类变量，它基本的无效假设 是(不包括配对资料)：
方法原理
❖ 卡方分布
▪ 显然，卡方值的大小不仅与A、E之差有关，还 与单.1元2 格数（自由度）有关
.10
.08
概率
.06
.04
.02
0.00
.00
4.02
8.04 12.06 16.08 20.10 24.12 28.14 32.16 36.18
2.01
6.03 10.05 14.07 18.09 22.11 26.13 30.15 34.17 38.19
2．计算概率和确定P值
▪ 本例n=a+b = 36 < 40，不满足2检验的应用
条件，宜采用四格表确切概率法。
方法原理
❖ 在四格表周边合计不变的条件下，在相应的总体 中进行抽样，四格表中出现各种排列组合情况的 概率 ▪ 本例即28、8、22、14保持不变的条件下，若H0 成立，计算出现各种四格表的概率
❖ 假设检验步骤如下：
▪ H0：两法总体阳性检出率无差别，即B = C ▪ H1：两法总体阳性检出率有差别，即B C
方法原理
根据 H0 得 b、c 两格的理论数均为 Tb = Tc = (b+c)/2，对 应的配对检验统计量为：
2 (b c)2 ,
bc
1
一般在 b + c < 40 时，采用确切概率法。