图练习题五章 梁的弯曲问题1剪力图与弯矩图
- 格式:pptx
- 大小:212.10 KB
- 文档页数:10

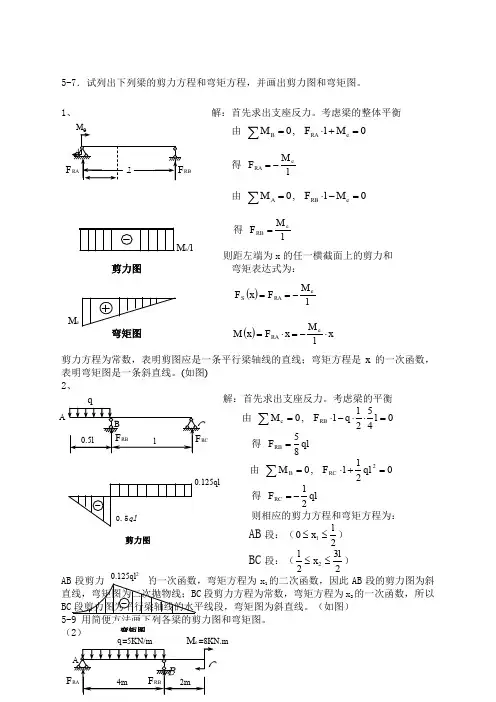
5-7.试列出下列梁的剪力方程和弯矩方程,并画出剪力图和弯矩图。
解:首先求出支座反力。
考虑梁的整体平衡由 0,0=+⋅=∑e RA B M l F M得 lM F eRA -= 由 0,0=-⋅=∑e RB A M lF M 得 lM F eRB =则距左端为x 的任一横截面上的剪力和剪力图 弯矩表达式为:()l M F x F eRA S -== ()x lM x F x M eRA ⋅-=⋅= 剪力方程为常数,表明剪图应是一条平行梁轴线的直线;弯矩方程是x 的一次函数,表明弯矩图是一条斜直线。
(如图)解:首先求出支座反力。
考虑梁的平衡 由 0452,0=⋅⋅-⋅=∑l l q l F M RB c得 ql F RB 85= 由 021,02=+⋅=∑ql l F M RC B得 ql F RC 21-=则相应的剪力方程和弯矩方程为:AB 段:(201lx ≤≤)BC 段:(2322lx l ≤≤)x 1的二次函数,因此AB 段的剪力图为斜段剪力方程为常数,弯矩方程为x 2的一次函数,所以剪力图解:由梁的平衡求出支座反力:AB段作用有均布荷载,所以AB段的剪力图为下倾直线,弯矩图为下凹二次抛物线;BC段没有荷载作用,所以BC段的剪力图为平行梁轴线的水平线段,弯矩图为直线。
在B支座处,剪力图有突变,突变值)的大大小等于集中力(支座反力FRB小;弯矩图有转折,转折方向与集中力方向一致。
(如图)(5)解:由梁的平衡求出支座反力:则其剪力为不定值,第一式的适用范围为。
由于截面B有集中力偶作用,则其弯矩也为不定值,第二式的适用范围为关于这个问题,待后面作进一步说明。
2、作剪力图和弯矩图剪力方程表明,梁各截面上的剪力都相等,因此剪力图应是一条平行于横轴的直线。
取直角坐标系x—,画出梁的剪力图为一水平直线。
因各横截面的剪力为负值,故画在横轴下面,如图(b)所示。
弯矩方程表明,弯矩M是x的一次函数,因此弯矩图应是一条倾斜直线。



5.4.1 梁的剪力、弯矩方程和剪力、弯矩图梁在外力作用下,各个截面上的剪力和弯矩一般是不相等的。
若以横坐标表示横截面沿梁轴线的位置,则剪力Q 和弯矩M 可以表示为坐标的函数,即它们分别称为梁的剪力方程和弯矩方程。
与绘制轴力图或扭矩图一样,可用图线表明梁的各截面上剪力和弯矩沿梁轴线的变化情况。
作图时,取平行于梁轴线的直线为横坐标轴,值表示各截面的位置;以纵坐标表示相应截面上的剪力、弯矩的大小及其正负,这种表示梁在各截面上剪力和弯矩的图形,称为剪力图和弯矩图。
例5-1 简支梁AB 承受承受均布荷载作用,如图 5 - 10a 所示。
试列出剪力方程和弯矩方程,并绘制剪力图和弯矩图。
图5-10解:(1) 计算支反力以整梁为研究对象,利用平衡条件计算支反力。
由于简支梁上的载荷对于跨度中央截面是对称的,所以 A 、 B 两端的支反力应相等,即(1)方向如图。
(2) 建立剪力、弯矩方程以梁左端A 为的坐标原点,取坐标为的任意横截面的左侧梁段为研究对象。
设截面上的剪力Q () 、弯矩M () 皆为正,如图5-10b 所示。
由平衡方程将(1) 式代入上面两式,解得( 2 )( 3 )(2) 、(3) 两式分别为剪力方程和弯矩方程。
(3) 绘制剪力图、弯矩图由式(2) 可知,剪力图为一直线。
只需算出任意两个截面的剪力值,如A 、B 两截面的剪力,即可作出剪力图,如图5 - 10c 所示。
由式(3) 可知,弯矩图为一抛物线,需要算出多个截面的弯矩值,才能作出曲线。
例如计算下列五个截面的弯矩值:当时, M =0 ;当时,;当时,。
由此作出的弯矩图,如图5-10d 所示。
由剪力图和弯矩图可知,在靠近A 、B 支座的横截面上剪力的绝对值最大,其值为在梁的中央截面上,剪力Q =0 ,弯矩为最大,其值为例5-2 简支梁AB 承受集中力偶M0作用,如图 5 - 11a 所示。
试作梁的剪力图、弯矩图。
图5-11解:(1) 计算支反力由平衡方程分别算得支反力为反力R A的方向如图,R B为负值,表示其方向与图 5 - 11a 中假设的方向相反。

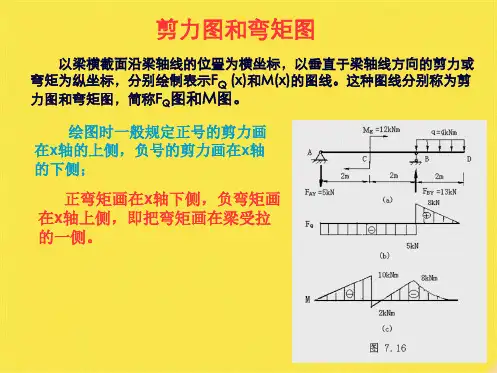



建筑类专业总复习十梁的剪力图和弯矩图的绘制例题:如图所示,已知外伸梁BC,在C端有集中力F=20kN作用。
(1)求A、B支座的约束反力;(2)画出梁的剪力图和弯矩图。
1.在梁的无荷载作用区,剪力图一般为,弯矩图为;当剪力图为正时,弯矩图为。
2.弯矩图一定画在一侧,这是为了在混凝土中。
3.在集中力作用处剪力发生,弯矩图发生。
在集中力偶作用处梁的剪力图,弯矩图发生,其绝对值等于。
4.梁的控制截面包括梁的起、止截面,均布荷载的起、止截面,集中力和集中力偶作用处截面和。
5.在简支梁上作用均布荷载,则其剪力图为线,弯矩图为,弯矩的最大值出现在,其值为。
6.梁剪力使为正。
7.在梁的集中力作用处,其左右两侧截面上弯矩情况分析正确的是。
()A.数值相同,符号相反B.数值不同,符号相同C.数值相同,符号相同D.数值不同,符号相反8.剪力为零的截面上,弯矩一定。
()A.取最大值B.取最小值C.取极值D.为零9.受满跨均布荷载作用的一简支梁,长为4.0m,离支座1.0m处的弯矩为12kN·m,则该梁的最大弯矩为。
()A.12kN·mB.4kN·mC.8kN·mD.16kN·m10.试画出图示悬臂梁的弯矩图。
11.作出ABC梁的剪力图和弯矩图。
12.如图所示外伸梁,请画出梁的剪力图与弯矩图。
13.一矩形截面木梁,其截面尺寸及荷载如图所示。
已知q=1.5kN/m,[σ]=10MPa,试计算:(1)A、B的支座反力。
(2)画出梁的内力图。
14.作出梁的剪力图和弯矩图。
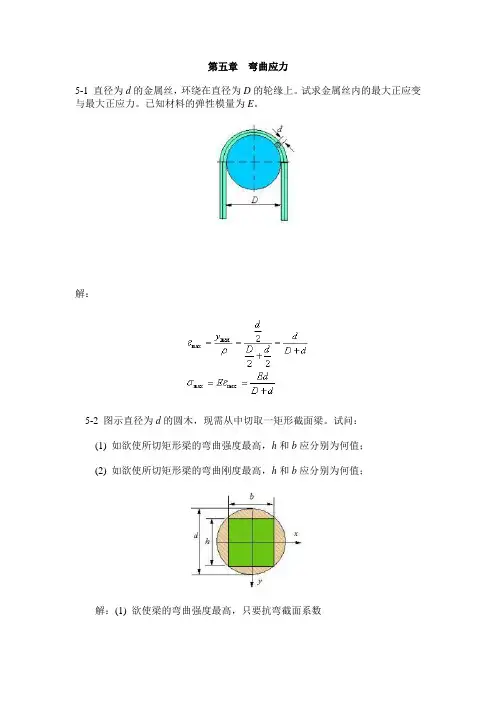
第五章弯曲应力5-1 直径为d的金属丝,环绕在直径为D的轮缘上。
试求金属丝内的最大正应变与最大正应力。
已知材料的弹性模量为E。
解:5-2 图示直径为d的圆木,现需从中切取一矩形截面梁。
试问:(1) 如欲使所切矩形梁的弯曲强度最高,h和b应分别为何值;(2) 如欲使所切矩形梁的弯曲刚度最高,h和b应分别为何值;解:(1) 欲使梁的弯曲强度最高,只要抗弯截面系数取极大值,为此令(2) 欲使梁的弯曲刚度最高,只要惯性矩取极大值,为此令5-3 图示简支梁,由№18工字钢制成,在外载荷作用下,测得横截面A 底边的纵向正应变ε=3.0×10-4,试计算梁内的最大弯曲正应力。
已知钢的弹性模量E =200GPa ,a =1m 。
解:梁的剪力图及弯矩图如图所示,从弯矩图可见:5-4 No.20a 工字钢梁的支承和受力情况如图所示。
若[]MPa 160=σ,试求许可载荷F 。
5-5 图示结构中,AB 梁和CD 梁的矩形截面宽度均为b 。
如已知AB 梁高为1h ,CD 梁高为2h 。
欲使AB 梁CD 梁的最大弯曲正应力相等,则二梁的跨度1l 和2l 之间应满足什么样的关系?若材料的许用应力为[σ],此时许用载荷F 为多大?5-6 某吊钩横轴,受到载荷kN 130F =作用,尺寸如图所示。
已知mm 300=l ,mm 110h =,mm 160b =,mm 75d 0=,材料的[]MPa 100=σ,试校核该轴的强度。
5-7 矩形截面梁AB,以固定铰支座A及拉杆CD支承,C点可视为铰支,有关尺寸如图所示。
设拉杆及横梁的[]MPaσ,试求作用于梁B端的许可载荷F。
=1605-8 图示槽形截面铸铁梁,F=10kN,M e=70kN·m,许用拉应力[σt]=35MPa,许用压应力[σc]=120MPa。
试校核梁的强度。
解:先求形心坐标,将图示截面看成一大矩形减去一小矩形惯性矩弯矩图如图所示,C截面的左、右截面为危险截面。
第6章典型习题解析1.简支梁受力如图a 所示。
试写出梁的剪力方程和弯矩方程,并作剪力图和弯矩图。
解:(1)求支座反力由平衡方程∑=0Bm和∑=0A m 分别求得ql R A 83=,ql R B 81=利用平衡方程∑=0y 对所求反力进行校核。
(2)建立剪力方程和弯矩方程以梁的左端为坐标原点,建立x 坐标,如图a 所示。
因在C 处分布载荷的集度发生变化,故分二段建立剪力方程和弯矩方程。
AC 段:qx ql x Q -=83)(1 )20(lx ≤<212183)(qx qlx x M -= )20(lx ≤≤CB 段: ql x Q 81)(2-= )2(l x l<≤)(81)(2x l ql x M -= )2(l x l≤≤3.求控制截面内力,绘Q 、M 图Q 图:AC 段内,剪力方程)(1x Q 是x 的一次函数,剪力图为斜直线,故求出两个端截面的剪力值,ql Q A 83=右,ql Q C 81-=左,分别以a 、c 标在x Q -坐标中,连接a 、c 的直线即为该段的剪力图。
CB 段内,剪力方程为常数,求出其中任一截面的内力值,例如ql Q B 81-=左,连一水平线即为该段剪力图。
梁AB 的剪力图如图b 所示。
M 图:AC 段内,弯矩方程)(1x M 是x 的二次函数,表明弯矩图为二次曲线,求出两个端截面的弯矩,0=A M ,2161ql M C =,分别以a 、c 标在x M -坐标中。
由剪力图知在d 点处0=Q ,该处弯矩取得极值。
令剪力方程0)(1=x Q ,解得l x 83=,求得211289)83(ql l M =,以d 点标在x M -坐标中。
据a 、d 、c 三点绘出该段的弯矩图。
CB 段内,弯矩方程)(2x M 是x 的一次函数,分别求出两个端点的弯矩,以c 、b 标在x M -坐标中,并连成直线。
AB 梁的M 图如图c 所示。
2.梁的受力如图a 示,利用微分关系作梁的Q 、M 图。