习题课一:剪力图与弯矩图的绘制
- 格式:ppt
- 大小:1.37 MB
- 文档页数:28

剪力图和弯矩图:悬臂梁的剪力图和弯矩图具体画法如下:内力图的规律:1、在无荷载作用区,当剪力图平行于x轴时,弯矩图为斜直线。
当剪力图为正时,弯矩图斜向右下;当剪力图为负时,弯矩图斜向右上。
2在均布荷载作用下的规律是:荷载朝下方,剪力往右降,弯矩凹朝上。
3、在集中力作用处,剪力图发生突变,突变的绝对值等于集中力的大小;弯矩图发生转折。
4、在集中力偶作用处弯矩图发生突变,突变的绝对值等于该集中力偶的力偶矩;剪力图无变化。
5、在剪力为零处有弯矩的极值弯矩图总结规律如下:1、在梁的某一段内,若无分布载荷作用,即q(x)=0,由d²M(x)/dx²=q(x)=0可知,M(x)是x的一次函数,弯矩图是斜直线。
2、在梁的某一段内,若作用分布载荷作用,即q(x)=常数,则d²M(x)/dx²=q(x)=常数,可以得到M(x)是x的二次函数。
弯矩图是抛物线。
3、在梁的某一截面内,若Fs(x)=dM(x)/dx=0,则在这一截面上弯矩有一极值(极大或极小)。
即弯矩的极值发生在剪力为零的截面上。
根据上述绘图规律可以准确画出悬臂梁在集中荷载下、均布荷载下的剪力图和弯矩图。
弯矩的叠加原理同一根粱AB受q、M0两种载荷作用、q单独作用及M0单独作用的三种受力情况。
在q、M0共同作用时:VA=ql/2+M0/l VS=ql/2+M0/l从计算结果中可以看到,梁的支座反力和弯矩都是荷载(q、M0)的一次函数,即反力或弯矩与荷载成线性关系。
这时,g、M0共同作用F所产生的反力或弯矩等于g与M0单独作用时所产生的反力或弯矩的代数和。
这种关系不仅在本例中存在,而且在其他力学计算中普遍存在,即只要反力、弯矩(或其他量)与载荷成线性关系,则若干个载荷共同引起的反力、弯矩(或其他量)等于各个载荷单独引起的反力、弯矩(或其他量)相叠加。
这种关系称为叠加原理。
应用叠加原理的前提是构件处在小变形情况下,这时各荷载对构件的影响各自独立。


作为一名土木工程师,在实际工作中,有时候要对软件(midas、sap2000、pkpm的计算结果有个判断)就要对结构的弯矩和剪力图有个大概的判断。
下面总结各种结构弯矩图的绘制及图例:
一、方法步骤
1、确定支反力的大小和方向(一般情况心算即可计算出支反力)
●悬臂式刚架不必先求支反力;
●简支式刚架取整体为分离体求反力;
●求三铰式刚架的水平反力以中间铰C的某一边为分离体;
●对于主从结构的复杂式刚架,注意“先从后主”的计算顺序;
●对于复杂的组合结构,注意寻找求出支反力的突破口。
2、对于悬臂式刚架,从自由端开始,按照分段叠加法,逐段求作M图(M图画在受拉一侧);对于其它形式的刚架,从支座端开始,按照分段叠加法,逐段求作M图(M图画在受拉一侧)。
二、观察检验M图的正确性
1、观察各个关键点和梁段的M图特点是否相符
●铰心的弯矩一定为零;
●集中力偶作用点的弯矩有突变,突变值与集中力偶相等;
●集中力作用点的弯矩有折角;
●均布荷载作用段的M图是抛物线,其凹凸方向与荷载方向要符合“弓箭法则”;
2、结构中的链杆(二力杆)没有弯矩;
3、结构中所有结点的杆端弯矩必须符合平衡特点。
各种结构弯矩图例如下:。

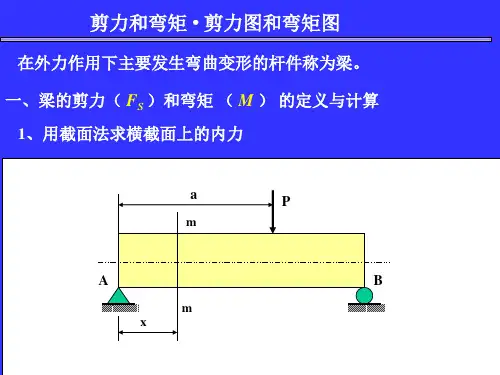

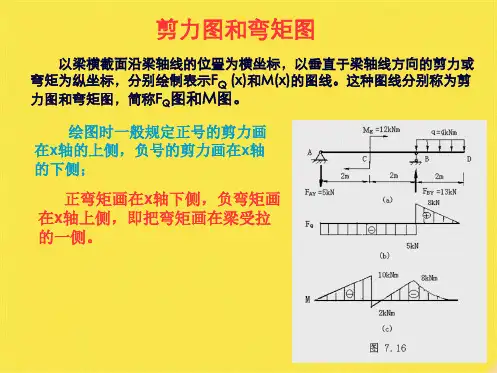



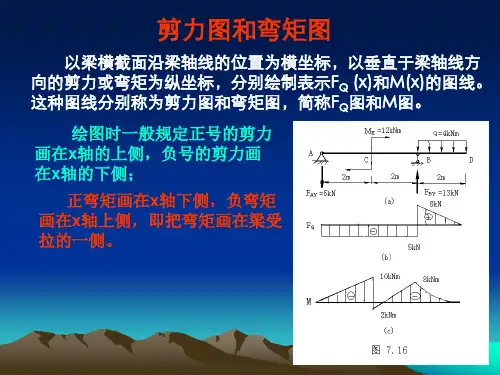
建筑类专业总复习十梁的剪力图和弯矩图的绘制例题:如图所示,已知外伸梁BC,在C端有集中力F=20kN作用。
(1)求A、B支座的约束反力;(2)画出梁的剪力图和弯矩图。
1.在梁的无荷载作用区,剪力图一般为,弯矩图为;当剪力图为正时,弯矩图为。
2.弯矩图一定画在一侧,这是为了在混凝土中。
3.在集中力作用处剪力发生,弯矩图发生。
在集中力偶作用处梁的剪力图,弯矩图发生,其绝对值等于。
4.梁的控制截面包括梁的起、止截面,均布荷载的起、止截面,集中力和集中力偶作用处截面和。
5.在简支梁上作用均布荷载,则其剪力图为线,弯矩图为,弯矩的最大值出现在,其值为。
6.梁剪力使为正。
7.在梁的集中力作用处,其左右两侧截面上弯矩情况分析正确的是。
()A.数值相同,符号相反B.数值不同,符号相同C.数值相同,符号相同D.数值不同,符号相反8.剪力为零的截面上,弯矩一定。
()A.取最大值B.取最小值C.取极值D.为零9.受满跨均布荷载作用的一简支梁,长为4.0m,离支座1.0m处的弯矩为12kN·m,则该梁的最大弯矩为。
()A.12kN·mB.4kN·mC.8kN·mD.16kN·m10.试画出图示悬臂梁的弯矩图。
11.作出ABC梁的剪力图和弯矩图。
12.如图所示外伸梁,请画出梁的剪力图与弯矩图。
13.一矩形截面木梁,其截面尺寸及荷载如图所示。
已知q=1.5kN/m,[σ]=10MPa,试计算:(1)A、B的支座反力。
(2)画出梁的内力图。
14.作出梁的剪力图和弯矩图。
剪力图和弯矩图1(基础)x轴,。
以表(a)C (c) (b)(1)(2)(3)≤l (4) 以剪力图是平行于x轴的直线。
AC 段的剪力为正,故剪力图在x轴上方;BC段剪力为负,故剪力图在x轴之下,如图8-12(b)所示。
由式(2)与式(4)可知,弯矩都是x的一次方程,所以弯矩图是两段斜直线。
根据式(2)、(4)确定三点x?0,M(x)?0 Fabl x?a,x?l,M(x)?0 M(x)?由这三点分别作出AC段与BC段的弯矩图,如图8-12(c)。
例8-4 简支梁AB受集度为q的均布载荷作用,如图8-13(a)所示,作此梁的剪力图和弯矩图。
图8-13解(1)求支反力由载荷及支反力的对称性可知两个支反力相等,即FA?FB?(2)列出剪力方程和弯矩方程以梁左端A为坐标原点,选取坐标系如图所示。
距原点为x的任意横截面上的剪力和弯矩分别为ql2 ql?qx2 0<x<l (1)xql1M(x)?FAx?qx?x?qx2222 0≤x≤l (2) FQ(x)?FA?qx?(3)作剪力图和弯矩图由式(1)可知,剪力图是一条斜直线,确定其上两点后即可绘出此梁的剪力图(图8-13b)。
由式(2)可知,弯矩图为二次抛物线,要多确定曲线上的几点,才能画出这条曲线。
例如通过这几点作梁的弯矩图,如图8-13(c)所示。
由剪力图和弯矩图可以看出,在两个支座内侧的横截面上剪力为最大值:FQmax?ql2。
1Mmax?ql28,而在此截面上剪力FQ?0。
在梁跨度中点横截面上弯矩最大例8-5 图8-14所示简支梁,跨度为l,在C截面受一集中力偶m作用。
试列出梁的FQ(x)M(x)AB剪力方程和弯矩方程,并绘出梁的剪力图和弯矩图。
图8-14解(1)求支反力由静力平衡方程?MA(x)?0,?MB(x)?0得FA?FB?(2)列剪力方程和弯矩方程由于集中力m作用在C处,全梁内力不能用一个方程来表示,故以C为界,分两段列出内力方程mlml 0<x≤a (1) AC段mM(x)?FAx?xl 0≤x<a (2)FQ(x)?FA?ml a≤x<l (3) BC段mM(x)?FAx?m?x?ml a≤x≤l (4)FQ(x)?FA?(3)画剪力图和弯矩图由式(1)、(3)画出剪力图,见图8-14(b);由式(2)(4)画出弯矩图,见图8-14(c)。