2020学年吉林省长春市东北师大附中高一(下)期末数学试题(解析版)

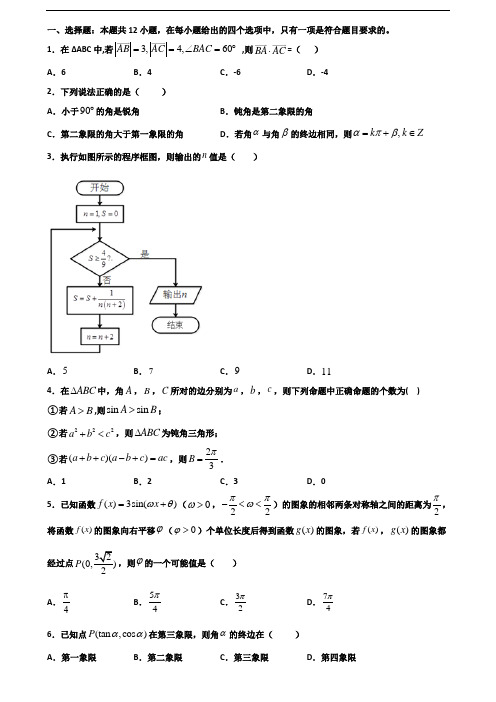
一、选择题：本题共12小题，在每小题给出的四个选项中，只有一项是符合题目要求的。

1．在ΔABC 中,若3,4,60AB AC BAC ==∠=︒ ,则BA AC ⋅=（ ） A ．6B ．4C ．-6D ．-42．下列说法正确的是（ ） A ．小于90︒的角是锐角B ．钝角是第二象限的角C ．第二象限的角大于第一象限的角D ．若角α与角β的终边相同，则,απβ=+∈k k Z3．执行如图所示的程序框图，则输出的n 值是（ ）A ．5B ．7C ．9D ．114．在ABC ∆中，角A ，B ，C 所对的边分别为a ，b ，c ，则下列命题中正确命题的个数为( ) ①若A B >,则sin sin A B >；②若222a b c +<，则ABC ∆为钝角三角形； ③若()()a b c a b c ac ++-+=，则23B π=． A ．1B ．2C ．3D ．05．已知函数()3sin()f x x ωθ=+（0>ω，22ππω-<<）的图象的相邻两条对称轴之间的距离为2π，将函数()f x 的图象向右平移ϕ（0ϕ>）个单位长度后得到函数()g x 的图象，若()f x ，()g x 的图象都经过点32(0,2P ，则ϕ的一个可能值是（ ） A ．4π B ．54π C ．32π D ．74π 6．已知点(tan ,cos )P αα在第三象限，则角α的终边在（ ） A ．第一象限B ．第二象限C ．第三象限D ．第四象限7．用数学归纳法证明()11113212224n n n n ++⋅⋅⋅+>≥++的过程中，设()111122k f k k k =++⋅⋅⋅+++，从n k =递推到1n k =+时，不等式左边为（）A ．()112k f k ++B ．()111212k k f k ++++ C ．()11112121k k f k k +++⋅⋅⋅+-++ D ．()11121k f k k ++-+8．已知双曲线2212x y a -=的焦点与椭圆22162x y +=的焦点相同，则双曲线的离心率为（ ）A ．22B ．2C ．3D ．29．函数2||22x y x =-在[]22-,的图像大致为 A ． B ．C ．D ．10．M 是ABC ∆边AB 上的中点，记a BC =，b BA =，则向量MC =( )A ．1-a-b 2 B ．1-a b 2+C ．1a-b 2D ．1a b 2+11．已知基本单位向量()1,0i =，()0,1f =，则34i f -的值为（） A ．1B ．5C ．7D ．2512．已知O ，N ，P 在ABC 所在平面内，且OA OB OC ==，0NA NB NC ++=，且PA PB PB PC PC PA ⋅=⋅=⋅，则点O ，N ，P 依次是ABC 的（ ）A ．重心 外心 垂心B ．重心 外心 内心二、填空题：本题共4小题13．在△ABC中，a、b、c分别为角A、B、C的对边，若b·cosC=c·cosB，且cosA＝23，则cosB的值为_____．14．把二进制数()2110011化为十进制数是：______．15．函数()21f x x x=+-的最大值为______.16．数列{}n a满足111nnaa+=-，112a=，则11a=___________．三、解答题：解答应写出文字说明、证明过程或演算步骤。

东北师大附中2022—2023学年下学期期末考试（高一）年级（数学）科试卷注意事项：1.答题前，考生须将自己的姓名、班级、考场座位号填写在答题卡指定位置上.2.回答选择题时，选出每小题答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑.如需改动.用橡皮擦干净后，再选涂其他答案标号.3.回答非选择题时，请使用0.5毫米黑色字迹签字笔将答案写在答题卡各题目的答题区域内，超出答题区域或在草稿纸、本试题卷上书写的答案无效，4.保持卡面清洁，不要折叠、不要弄皱、弄破，不准使用涂改液、修正帮、刮纸刀. 本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，满分120分.考试用时120分钟.第Ⅰ卷（选择题 共48分）一、单项选择题（本题共8小题，每小题4分，共32分.在每小题给出的四个选项中，只有一项是符合题目要求的）1. 已知()1i 6z −=，则z =（ ）A. 3i −−B. 3i −C. 33i −+D. 33i +【答案】D 【解析】【分析】根据复数的除法运算计算即可.【详解】由()1i 6z −=， 得()()()61i 633i 1i1i 1i z +===+−−+.故选：D .2. 已知向量()2,1a =，(),1b m =− ，若()a b a −⊥，则实数m =（ ）A. 3B. 3−C. 4D. 4−【答案】A 【解析】【分析】根据向量垂直的坐标表示，列式计算，即得答案. 【详解】因为()a b a −⊥ ，故()0a b a −⋅=，由题意得(2,2)a b m −=−，故2(2)20m −+=，解得3m =， 故选：A3. 已知ABC 的内角A ，B ，C 的对边分别是a ，b ，c ，16a =，8b =，60A =°，则cos B =（ ）A.B.C.D.【答案】D 【解析】【分析】利用正弦定理求解即可. 【详解】因为sin sin a bA B=，所以sin sin b A B a ==因为a b >，所以60B A <=°，所以cos B . 故选：D.4. 已知两条不同直线,l m 与两个不同平面,αβ，下列命题正确的是 A. 若//,l l m α⊥，则m α⊥ B. 若,//l l αβ⊥，则αβ⊥ C. 若//,//l m αα，则//l m D. 若//,//m αβα，则//m β【答案】B 【解析】 【分析】在A 中，可能,m α⊥也可能//m α；在B 中，由线面垂直的性质定理得αβ⊥；在C 中，可能l ⊥m ，也可能//l m ；在D 中，可能//m β，也可能.m β⊂ 【详解】由l ，m 为两条不同的直线，α，β为两个不同的平面，知： 在A 中，若//,l l m α⊥，则可能,m α⊥也可能//m α，故A 错误； 在B 中，若,//l l αβ⊥，则由线面垂直的性质定理得,αβ⊥故B 正确； 在C 中，若//,//l m αα，则可能l ⊥m ，也可能//l m ,故C 错误；在D 中，若//,//m αβα，则可能//m β，也可能m β⊂，故D 错误． 故选B ．【点睛】本题考查命题真假的判断，考查空间中线线、线面、面面间的位置关系等基础知识，考查推理论证能力、空间想象能力，是中档题．5. 2023年吉林省高考分数公布后，附中再续辉煌，高三一班平均分657分，其中的12名同学成绩分别是（单位：分）：673，673，677，679，682，682，684，685，687，691，697，705，则这12名学生成绩的第75百分位数是（ ） A. 689 B. 687C. 679D. 678【答案】A 【解析】【分析】根据百分位数计算规则计算可得.【详解】因为1275%9×=，所以数据的第75百分位数为从小到大排列的第9、第10两数的平均数， 即6876916892+=，即则这12名学生成绩第75百分位数是689. 故选：A6. 在边长为2的正三角形ABC 中，13AD DB = ，CE EB = ，则AE DE ⋅=（ ）A. 94−B. 32C. 32− D. 94 【答案】D 【解析】【分析】建立平面直角坐标系，得到向量的坐标，利用数量积运算求解. 【详解】解：建立如图所示平面直角坐标系：则((),1,0A B −设(),D x y，则((),,1,AD x y DB x y ==−−−，因为13AD DB = ，的所以113313x x y y=−− =−，解得14x y =− =，即14D − ，则(10,,,4AE DE = ，所以94AE DE ⋅= ，故选：D7. 《九章算术》中将底面为直角三角形且侧棱垂直于底面的三棱柱称为堑堵、在堑堵111ABC A B C 中，若14AB BC AA ===，若P 为线段1BA 中点，则点P 到平面11A B C 的距离为（ ）A. 1B.C.D. 4【答案】C 【解析】【分析】利用等积法可求B 到平面11A B C 的距离，进而可求点P 到平面11A B C 的距离. 【详解】因为ABC 为直角三角形，且AB BC =，易知AB BC ⊥，而1AA ⊥平面ABC ，BC ⊂平面ABC ，故1AA BC ⊥，同理1AA AC ⊥，1BB BC ⊥，而11,,AA AB A AA AB ∩=⊂平面1ABB ，故BC ⊥平面1ABB ，故111111324443323C AB B A B B V BC S −=××=××××= ，又AC1A C =，而1B C ，故2221111B C B A A C +=， 所以111A B B C ⊥，故11111113243323B A BC A B C V d S d d −=××=××××==， 其中d 为B 到平面11A B C的距离，故d =而P 为线段1BA 中点，故P 到平面11A B C .故选：C.8. 已知G 为ABC 的重心，150A ∠=°，AB AC ⋅，则AG 的最小值为（ ）A.B.C.D.【答案】C 【解析】【分析】取BC 的中点D ，连接AD ，即可得到()13AG AB AC =+，根据数量积的定义得到2AB AC ⋅= ，利用基本不等式求出22AB AC + 的最小值，再由()2219AG AB AC =+ 及数量积的运算律求出AG 的最小值.【详解】取BC 的中点D ，连接AD ，则()()22113323AG AD AB AC AB AC ==×+=+，又150A ∠=°，AB AC ⋅，所以cos AB AC AB AC BAC ⋅=⋅∠ ，所以2AB AC ⋅= ，所以2224AB AC AB AC +≥⋅=时取等号，所以()()222211299AG AB AC AB AB AC AC =+=+⋅+()22129AB AB AC AC +⋅+((211499AB =−≥− 时取等号，所以minAG==故选：C二、多项选择题（本题共4小题，每小题4分，共16分，在每小题给出的四个选项中，有多项符合题目要求.全部选对得4分，部分选对得2分，有选错或不选得0分）9. 下列说法错误的是（）A. 以直角三角形的一边所在直线为轴旋转一周所得的旋转体是圆锥B. 用一个平面去截棱锥，底面和截面之间部分所围成的几何体是棱台C. 边长为2D. 用一个平面去截取正方体，得到的截面可能是正六边形【答案】AB【解析】【分析】当旋转轴为斜边时即可判断A，根据棱台的定义判断B，根据直观图与平面图面积的关系判断C，作出截面在判断形状，即可判断【详解】对于A：以直角三角形的一条直角边所在直线为轴旋转一周所得的旋转体是圆锥，以斜边所在直线为轴旋转一周所得的旋转体是两个同底的圆锥所拼接而成的几何体，故A错误；对于B：用一个平行底面的平面去截棱锥，底面和截面之间部分所围成的几何体是棱台，故B错误；对于C：边长为222C正确；对于D：一个平面与正方体的6个面相交，截面为六边形，此六边形可能是正六边形，如图，N、P、Q、R、S、T为正方体所在棱的中点，顺次连接得正六边形，设正方体棱长为a，有TN NP PQ QR RS ST ======，PT =， 在NPT 中，2221cos 22NT NP PT PNT NT NP +−∠==−⋅，则120PNT ∠= ，同理120NPQ PQR QRS RST STN ∠=∠=∠=∠=∠= ，即六边形NPQRST 为正六边形，故D 正确. 故选：AB10. 东北师大附中培养的学生德才兼备、全面发展、在校团委领导下的各个社团，积极开展各项活动，其中甲、乙两个社团为了钠新，利用7天的时间进行宣传，将每天宣传次数绘制成如下频数分布折线图（其中前三天宣传次数相同），则下列说法正确的是（ ）A. 甲社团众数小于乙社团众数B. 甲社团的平均数小于乙社团的平均数C. 甲社团的极差大于乙社团的极差D. 甲社团的方差大于乙社团的方差【答案】ACD 【解析】【分析】根据众数，平均数，极差，方差的公式计算即可.【详解】甲7天的次数依次为2,2,3,2,5,4,3，乙7天的次数依次为2,2,3,4,3,3,4， 对于A ，甲的众数为2，乙的众数为3， 则甲社团众数小于乙社团众数，故A 正确； 对于B ，甲社团的平均数为223254337++++++=，乙社团的平均数为223433437++++++=， 则甲社团的平均数等于乙社团的平均数，故B 错误；对于C ，甲社团极差为523−=，乙社团的极差422−=， 则甲社团的极差大于乙社团的极差，故C 正确； 对于D ，甲社团方差为()()()()()()()2222222182323332353433377−+−+−+−+−+−+−= ，的的乙社团的方差为()()()()()()()2222222142323334333334377−+−+−+−+−+−+−= ， 则甲社团的方差大于乙社团的方差，故D 正确. 故选：ACD .11. 在ABC 中，内角A ，B ，C 所对的边分别为a ，b ，c ，则下列说法正确的是（ ） A. 若60A =°，a =ABC 的外接圆半径为1 B. 若60A =°，a =ABCC. 若60A =°，2b =，且ABC为直角三角形，则a =D. 若60A =°，2b =，且ABC 有两解，则a2a << 【答案】ABD 【解析】【分析】利用正弦定理即可判断A ；根据余弦定理结合基本不等式及三角形的面积公式即可判断B ；分90B =°和90C=°两种情况讨论即可判断C ；要使ABC 有两解，则60120B °<<°且90B ≠°，再结合正弦定理即可判断D .【详解】对于A ，因为60A =°，a =所以ABC的外接圆半径为1112sin 2a A ⋅=×=，故A 正确； 对于B ，若60A =°，a =由余弦定理可得222222cos a b c bc A b c bc bc =+−=+−≥， 所以3bc ≤，当且仅当b c ==时，取等号，则1sin 2ABC S bc A =≤△， 即ABCB 正确； 对于C ，当90B =°时，则sin ab A =，当90C =°时，则tan a b A =综上，a =C 错误； 对于D ，60A =°，2b =，因为sin sin a b A B =，所以sin sin b AB a==， 因为60A =°，所以0120B °<<°，要使ABC 有两解，则60120B °<<°且90B ≠°sin 1B <<，1<<2a <<，故D 正确. 故选：ABD.12. 在正方体1111ABCD A B C D −中，1AB =.点P 在正方体的面11CC D D 内（含边界）移动，则下列结论正确的是（ ）A. 当直线1B P ∥平面1A BD 时，则直线1B P 与直线1CD 所成的大小可能为π4B. 当P 正方形11CC D D 的中心时，Q 为线段11C D 上的动点，则1PQ QB +C. 若直线1B P 与平面11CC D D 所成角为π4，则点P 的轨迹长度为π2D. 当直线1B P AB ⊥时，Q 为线段11C D 中点，则三棱锥1P AQA −的体积为定值 【答案】BCD 【解析】【分析】应用线面平行、面面平行的判定证面1//A BD 面11CB D ，进而判断P 的轨迹，即可判断线线角的范围，从而判断A ；将平面1111D C B A 与平面11C D DC 展开，即可判断B ；根据11B C ⊥面11CC D D ，结合线面角大小确定P 的轨迹，即可求长度，从而判断C ；得到点P 在1CC 上运动，即可判断D . 【详解】对于A ，如下图，连接1CB 、1CD 、11B D ，由正方体性质知：11//CB DA ，11//CD BA ，由1CB ⊄面1A BD ，1DA ⊂面1A BD ，则1//CB 面1A BD ，同理可证1//CD 面1A BD ， 又11CB CD C = ，11,CB CD ⊂面11CB D ，故面1//A BD 面11CB D ，由1B ∈面11CB D ，面11CB D ∩面111CC D D CD =，且P 在正方体的面11CC D D 内，所以，要使直线1//B P 平面1A BD ，则1B P ⊂面11CB D ，即1P CD ∈，又△11CB D 为等边三角形， 故P 在1CD 上运动时，直线1B P 与直线1CD 成角为ππ,32，故A 错误；对于B ，将平面1111D C B A 与平面11C D DC 展开，得到如下所示图形，当P 正方形11CC D D 的中心时，即为1CD 与1C D 的交点，做1PH CC ⊥，连接1PB ，与11C D 交于点Q ，则此时1PQ QB +最小，即为1PB ，且1122PH CD ==，113122B H =+=，则1PB ，故B 正确； 对于C ，由11B C ⊥面11CC D D ，显然11B D 、1B C 与面11CC D D 夹角为π4，所以，要直线1B P 与平面11CC D D 所成角为π4，则P 轨迹是以1C 为圆心1CD 为半径的14圆， 如下图示：所以，轨迹长度为1π2π42×=，故C 正确； 对于D ，建立如下图所示的空间直角坐标系，则可得()()()10,0,0,1,0,0,1,0,1A B B ，设(),1,P x z ，则()1,0,0AB = ，()11,1,1B P x z =−−，当直线1B P AB ⊥时，可得110AB B P x ⋅=−=，即1x =，所以点P 在1CC 上运动，则1AA P 的面积为定值，所以三棱锥1P AQA −的体积为定值， 故D 正确； 故选：BCD三、填空题，本题共4小题，每小题4分，共16分.13. 数据12,,,n x x x 的平均数是2，方差是1，则数据125x +，225x +， ，25n x +的平均数与方差之和是______. 【答案】13 【解析】【分析】根据平均数与方差的性质计算即可.【详解】因为数据12,,,n x x x 的平均数是2，方差是1，所以数据125x +，225x +， ，25n x +的平均数为2259×+=，方差为2214×=， 所以所求为9413+=.故答案为：13.14. 在数学中，二阶行列式a bad bc c d=−，若在复数域内，12i z =，21i z =+，32z z =，在当12340z z z z =时，4z =______. 【答案】1 【解析】【分析】确定3z ，根据二阶行列式的的含义，结合复数的乘除法，列式计算求得4z ，即可求得答案. 【详解】由题意得321i z z ==−， 故由12340z z z z =可得14230z z z z −=，即2341(1i)(1i)1i 2i iz z z z +−====−，故41z =， 故答案为：115. 一船向正北方向匀速行驶，看见正西方向两座相距20海里的灯塔恰好与该船同一直线上，继续航行半小时后，看见其中一座灯塔在南偏西45°方向上，另一灯塔在南偏西75°方向上，则该船的速度是______海里/小时.【答案】)201−【解析】【分析】依题意画出图形，设BA x =，得到CA x =，然后在Rt BAD 中利用锐角三角函数求出x ，即可求出速度.【详解】如图所示：设船的初始位置为A ，半小时后行驶到B ，两个灯塔分别位于C 和D ， 所以=45ABC ∠°，75ABD ∠=°，则30CBD ∠=°，15CDB ∠=°，所以()tan tan15tan 4530CDB∠=°=°−°tan 45tan 3021tan 45tan 30°−°==−+°° 设BA x =（海里），则CA x =（海里），在Rt BAD 中，20DA x =+，则tan 220AB xCDB ADx ∠===−+，解得)110x =−，所以船速为))11012012−÷=−（海里/小时）.故答案为：)201−16. 青铜豆最早见于商代晚期，盛行于春秋战国时期，它不仅可以作为盛放食物的铜器.还是一件十分重要的礼器，图①为河南出土的战国青铜器——方豆，豆盘以上是长方体容器和正四棱台的斗形盖.图②是与主体结构相似的几何体，其中4AB =，2MN NF ==，K 为BC 上一点，且13CK BC =，Z 为PQ 上一点.若DK MZ ⊥，则QZZP=______；几何体EFGH MNPQ −的所有顶点都在同一个球面上，则该球的表面积为______.【答案】 ①. 12##0.5 ②. 40π【解析】【分析】设面EMZ 交平面ABCD 于AJ ，利用面面平行的性质作出//MZ AJ ，证明出DCK ADJ ，得到:CJ JD BK KC =：，即可求出答案；先判断出球心在面NFHQ 上，设NQ 的中点为1O ,FH 的中点为2O ,则球心在O 在12O O 上，设外接球的半径为R ，2OO d =.利用半径相等列方程，解出d ，即可求出R =计算出外接球的表面积.【详解】由题意可知：面ABCD //面EFGH //面MNPQ ，设面EMZ 交平面ABCD 于AJ ，因为面EMZ 交平面=MNPQ ZM ，所以//MZ AJ ， 设DK AJ L ∩=，因为DK MZ ⊥，所以DK AJ ⊥，因为ππ,22DKC KDCDJL KDC ∠+∠=∠+∠=，所以DKC DJL ∠=∠， 而π2DCK ADJ ∠=∠=，所以DCK ADJ ， 所以CK DCDJ AD =，所以CK DJ DC AD=， 因为四边形ABCD 为正方形，所以::2:1CJ JD BK KC ==.所以12QZDJ ZPJC ==， 几何体EFGH MNPQ −为正四棱台，由正四棱台的对称性可知， 几何体EFGH MNPQ −外接球的球心必在平面NFHQ 上， 设NQ 的中点为1O ，FH 的中点为2O ，则球心在O 在12O O 上，由题意可知：FH =NQ21FO NO ，过N 作NS 垂直FH 于S ，则()(1122FS FH NQ =−=−=，由勾股定理得：NS，所以12O O NS ==设外接球的半径为R ，2OO d =， 由R OF ON ==，=，解得：d =的所以R OF =，几何体EFGH MNPQ −外接球的表面积为24π40πS R =，故答案为：12；40π.【点睛】方法点睛：求多面体的外接球的面积和体积问题，常用方法有：（1）三条棱两两互相垂直时，可恢复为长方体，利用长方体的体对角线为外接球的直径，求出球的半径；（2）直棱柱的外接球可利用棱柱的上下底面平行，借助球的对称性，球心为上下底面外接圆的圆心连线的中点，再根据勾股定理求球的半径；（3）如果涉及几何体有两个面相交，可过两个面的外心分别作两个面的垂线，垂线的交点为几何体的球心.四、解答题：本题共6小题.共56分、解答应写出文字说明、证明过程或演算步骤.17. 如图.已知正三棱柱111ABC A B C -的底面边长6AB =，D ，E 分别是1CC ，BC 的中点，AE DE =.（1）三棱锥A ECD −的体积； （2）正三棱柱111ABC A BC -的表面积. 【答案】（1（2）+【解析】【分析】（1）依题意可得AE BC ⊥，在由正三棱柱性质得到1CC BC ⊥，利用勾股定理求出线段的长度，最后由13A ECD D AECAEC V V S CD −−==⋅ 计算可得； （2）求出上下底面积及侧面积，即可求出棱柱的表面积. 【小问1详解】因为E 是BC 的中点，ABC 为等边三角形，所以AE BC ⊥，的在正三棱柱111ABC A B C 中1CC ⊥平面ABC ，BC ⊂平面ABC ，所以1CC BC ⊥，又6AB =，所以3EC =，=AE AE DE =，所以CD =所以132AEC S =××=所以1133A ECD D AEC AEC V V S CD −−==⋅=× . 【小问2详解】由（1）可知12CC CD ==，111162ABC A B C S S ==××=136ABC S C CC =⋅=××= 侧所以棱柱的表面积2S =×++18. 近年来，“直播带货”受到越来越多人的喜爱.目前已经成为推动消费的一种流行的营销形式.对某直播平台的直播商家进行调查统计，发现所售商品多为小吃、衣帽、生鲜、玩具、饰品类等，各类直播商家所占比例如图①所示.（1）该直播平台为了更好地服务买卖双方，打算随机抽取80个直播商家进行问询交流.如果按照比例分配分层抽样的方式抽取，则应抽取小吃类、玩具类商家各多少家？（2）在问询了解直播商家的利润状况时，工作人员对抽取的80个商家的平均日利润进行了统计（单位：元），所得频率分布直方图如图②所示.请根据频率分布直方图，求出图中a 的值，并估计该直播平台商家日利润的平均数（求平均数时同一组中的数据用该组区间的中点值作代表）. 【答案】（1）小吃类32家，玩具类8家. （2）0.002a =；平均数为377.5. 【解析】【分析】（1）根据题意，直接计算，即可得到结果；（2）根据题意，先由频率之和求得a ，再根据平均数的计算公式即可得到结果. 【小问1详解】由题意可得，()80125%15%10%5%5%32×−−−−−=，8010%8×=，所以应抽取小吃类32家，玩具类8家. 【小问2详解】由题意可得，()0.00130.0030.0050.007501a ×++++×=，解得0.002a =， 平均数为()2500.0013000.0033500.0074000.0054500.0025000.0015500.00150×+×+×+×+×+×+××377.5=，所以该直播平台商家日利润的平均数为377.5.19. 如图，在四边形OBCD 中，2OB DC = ，2OA AD =，OB OD ⊥，且1ADCD == .（1）用OA ，OB 表示BC；（2）点P 在线段AC 上，且2AC AP .求BC 与BP夹角θ的余弦值.【答案】（1）3122BC OA OB =−（2 【解析】【分析】（1）根据向量的线性运算，即可求得答案；（2）建立平面直角坐标系，求得相关点坐标，求出BC 与BP的坐标，根据向量的夹角公式即可求得答案.【小问1详解】 由2OB DC =，可知OB DC ∥，由2OA AD =，可知A 为OD 的靠近D 的三等分点，故31312222BC BO OD DC OB OA OB OA OB =++=−++=−；因为OB OD ⊥，故以O 为坐标原点，以,OD OB 为,x y 轴，建立平面直角坐标系，而1ADCD == ，故2OA OB == ,则),),,(20(02)1,,(3A B C ，故(1,1)AC = ，(3,1)BC =− ，由2AC AP = ，可得522,1P，故,5322BP=−，故cos cos ,BC BPBC BP BC BPθ⋅=〈〉==20. 如图，四棱锥P ABCD −的底面是正方形，PA ⊥底面ABCD ，2AP AB ==，E 是棱PB 的中点.（1）证明：直线⊥AE 平面PBC ；（2）求直线DE 与平面P AD 所成角的余弦值. 【答案】（1）证明见解析 （2【解析】【分析】（1）依题意可证BC⊥平面PAB ，即可得到AE BC ⊥，再由AE PB ⊥，即可得证；（2）取AP 的中点H ，连接EH ，即可证明EH ⊥平面PAD ，则EDH ∠即为DE 与平面PAD 所成的角，再由锐角三角函数计算可得.因为PA ⊥底面ABCD ，BC ⊂底面ABCD ，所以PA BC ⊥， 又AB BC ⊥，AB PA A = ，,AB PA ⊂平面PAB ， 所以BC⊥平面PAB ，又AE ⊂平面PAB ，所以AE BC ⊥，因为AP AB =，E 为PB 的中点，所以AE PB ⊥，BC PB B = ，,BC PB ⊂平面PBC ，所以⊥AE 平面PBC .【小问2详解】取AP 的中点H ，连接EH ，则//EH AB ，因为PA ⊥底面ABCD ，,AB AD ⊂底面ABCD ，所以PA AB ⊥，PA AD ⊥， 又AB AD ⊥，所以EH PA ⊥，EH AD ⊥，PA AD A ∩=，,PA AD ⊂平面PAD ， 所以EH ⊥平面PAD ，DH ⊂平面PAD ，所以EH DH ⊥， 所以EDH ∠即为DE 与平面PAD 所成的角，又112EH AB ==，DH =，DE ==，所以cos DH EDH ED ∠=，即直线DE 与平面PAD 所成角的余弦值为21. 已知在锐角ABC 中，内角A ，B ，C 所对的边分别为a ，b ，c ，2sin cos c a C b C −=−.（1）求角B ；（2）若b =，D 为AC 的中点，求线段BD 长度的取值范围. 【答案】（1）π3（2）【解析】【分析】（1）由2sin cos c aC b C −=−，利用正弦定理得到2sin sin sin sin cos C AB C B C −=−，再结合理解和的余弦公式化简为πsin 16B+=求解； （2）根据D 为AC 的中点，得到()12BD BC BA =+ ，从而有()22214BD a c ac =++，再由余弦定理得到 2212a c ac +−=，得到()2162BDac =+，然后由 222π4sin sin 4sin sin 3ac R A C R A A ==−π8sin 246A−+，利用三角函数的性质求解.【小问1详解】解：因为2sin cos c aC b C −=−，所以()2sin sin sin sin cos C B C B C B C −+=−，2sin cos sin sin C B C B C −，因为(),0,πB C ∈，所以2cos B B −，cos 2B B +=，则πsin 16B+=， 所以ππ62B +=，则π3B =；【小问2详解】 因为D 为AC 的中点，所以()12BD BC BA =+， 则()222124BD BC BC BA BA =+⋅+ ，即 ()22214BD a c ac =++， 由余弦定理得 2222cos b a c ac B =+−，即 2212a c ac +−=，所以 ()2162BDac =+， 三角形外接圆的半径为 24sin bR B==，则 222π4sin sin 4sin sin 3ac R A C R A A ==−，2cos 8sin A A A +，24cos 24A A =−+， π8sin 246A −+， 因为ABC 是锐角三角形，所以 π02π02A C << <<，即 π022ππ032A A << <−< ，解得 ππ62A <<， 则 ππ5π2,666A −∈ ，则 π1sin 2(,1]62A −∈， 所以 (8,12]ac ∈，则 2(7,9]BD ∈， 所以BD ∈，即线段BD长度的取值范围为：.22. 如图，在正方形ABCD 中，点E 、F 分别为AB 、BC 的中点，将AED △，DCF 分别沿DE 、DF 折起，使A ，C 两点重合于P ，连接EF .（1）点M 是PD 上一点.若PB //平面EFM ，则PM MD为何值？并说明理由； （2）点M 是PD 上一点，若3MD PM =，求二面角M EF D −−的余弦值.【答案】（1）13，理由见解析 （2【解析】【分析】（1）连BD 交EF 于G ，连MG ，根据平面几何知识得14BG BD =，根据线面平行的性质定理得//PB MG ，从而可得答案；（2）证明PD ⊥平面PEF ，EF ⊥平面PBD ，推出MGD ∠是二面角M EF D −−的平面角，由PD ⊥平面PEF ，推出PD PG ⊥，设正方形ABCD 的边长为4，解三角形可得结果.【小问1详解】连BD 交EF 于G ，连MG ，因为在正方形ABCD 中，点E 是AB 的中点，点F 是BC 的中点，则G 为EF 的中点，1124BG AB BD =, 因为PB //平面EFM ，PB ⊂平面PBD ，平面PBD 平面EFM MG =，所以//PB MG ，所以14PM BG PD BD ==，所以13PM MD =； 【小问2详解】由（1）知，若3MD PM =，则//PB MG ，因为AE AD ⊥，CF CD ⊥，所以PE PD ⊥，PF PD ⊥，又PE PF P = ，,PE PF ⊂平面PEF ，所以PD ⊥平面PEF ，因为EF ⊂平面PEF ，所以PD EF ⊥，因为在正方形ABCD 中，点E 是AB 的中点，点F 是BC 的中点，所以EF BD ⊥，因为PD BD D ∩=，,PD BD ⊂平面PBD ，所以EF ⊥平面PBD ，又,MG GD ⊂平面PBD ，所以MG EF ⊥，GD EF ⊥，又MG ⊂平面EFM ，GD ⊂平面DEF ，平面EFM 平面DEF EF =，所以MGD ∠是二面角M EF D −−的平面角.因为PD ⊥平面PEF ，PG ⊂平面PEF ，所以PD PG ⊥，设正方形ABCD 的边长为4，则BD =，34GD BD ==，114PM PD ==，3MD =,所以PG ，MG =222cos 2MG GD MD MGD MG GD +−==⋅−−. 即二面角M EF D。

2019-2020学年吉林省长春市实验中学高一下学期期末考试数学（理）试题一、单选题1．已知数列{}n a 满足114n n a a +=，若3416a a +=，则54a a +=（ ） A ．12B ．1C ．4D ．8【答案】C【解析】由已知可得数列{}n a 为等比数列，由等比数列的性质可得答案. 【详解】数列{}n a 满足114n n a a +=，即114n n a a +=，可知数列为公比14q =的等比数列， ()544311644a a a a q +=+=⨯=， 故选：C 【点睛】本题考查等比数列的定义和等比数列性质的应用，属于基础题.2．某篮球队甲、乙两名运动员练习罚球，每人练习10组，每组罚球40个.命中个数的茎叶图如图，则下面结论中错误．．的一个是（ ）A ．甲的极差是29B ．甲的中位数是23C ．甲罚球命中率比乙低D ．乙的众数是21【答案】C【解析】根据统计量的计算方法，逐个计算，即可得解. 【详解】对A ，37-8=29，正确，对B ，第五、六两位分别为2224、，故中位数为22+242， 对C ，甲的平均数为8+12+13+20+22+24+25+26+27+37=21.410，乙的平均数为9+11+13+14+18+19+20+21+21+23=16.910，显然甲的平均数大，故C 错误；对D ，由茎叶图观察可知有两个21，故21为众数，故D 正确. 故选：C. 【点睛】本题考查了通过茎叶图求极差、中位数、平均数以及众数，考查了对各个概念的理解以及一定量的计算，属于简单题.3．将给定的9个数排成如图所示的数表，若每行3个数按从左至右的顺序构成等差数列，每列的3个数按从上到下的顺序也构成等差数列，且表正中间一个数22a 2=，则表中所有数之和为( )A ．2B ．18C ．20D ．512【答案】B【解析】根据每行数的和等于第二个数的3倍，每列数的和等于第2个数的3倍，可得表中所有数之和为229a ，据此即可求出表中所有数之和． 【详解】每行3个数按从左至右的顺序构成等差数列，111213123a a a a ∴++=， 212223223a a a a ++=，313233323a a a a ++=，每列的3个数按从上到下的顺序也构成等差数列，122232223a a a a ∴++=，∴表中所有数之和为2299218a =⨯=，故选B ．【点睛】本题主要考查等差数列的性质，意在考查灵活应用所学知识解答问题的能力，属于基础题．4．若0a b >>，则下列不等式中一定成立的是（ ）A ．11a b b a +>+B ．11b b a a +>+ C ．11a b b a->-D ．22a b aa b b+>+ 【答案】A【解析】特值法取21a b =，=，排除B 与D ；讨论函数1()f x x x =- 和1()g x x x=+ 的单调性可得到答案. 【详解】取21a b =，=，排除B 与D ； 函数1()f x xx=-是(0)+∞，上的增函数，当0a b >>时，()()f a f b >必定成立， 即1111a b a b a b b a->-⇔+>+，所以A 正确函数1()g x x x=+在(01]，上递减，在[1)+∞，上递增，当0a b >>时， ()()g a g b >不一定成立，所以C 不成立 故选：A 【点睛】本题考查利用不等式的性质比较大小，此类小题通常采取特值法进行排除，属于基础题. 5．某几何体的三视图如图所示，则该几何体的体积为( )A ．1B ．2C ．3D ．6 【答案】B【解析】画出几何体的图形，利用三视图的数据求解几何体的体积即可．【详解】解：由题意可知几何体的形状如图：1AC =，2CD =，3BC =，AC CD ⊥，BCDE 是矩形，AC BC ⊥，所以几何体的体积为：123123⨯⨯⨯=． 故选B ． 【点睛】本题考查几何体的体积的求法，三视图与几何体的对应关系的判断是解题的关键． 6．在一组样本数据为11(,)x y ，22(,)x y ，，(,)n n x y （2n ≥，1x ，2x ，3x ，，n x 不全相等）的散点图中，若所有样本点()(,1,2,,)i i x y i n =都在直线123y x =-+上，则这组样本数据的相关系数为（ ） A ．13- B ．13C ．1D ．-1【答案】D【解析】根据回归直线方程可得相关系数． 【详解】根据回归直线方程是y 13=-x +2， 可得这两个变量是负相关，故这组样本数据的样本相关系数为负值， 且所有样本点（x i ，y i ）（i ＝1，2，…，n ）都在直线上，则有|r |＝1， ∴相关系数r ＝﹣1． 故选D ． 【点睛】本题考查了由回归直线方程求相关系数，熟练掌握回归直线方程的回归系数的含义是解题的关键．7．在△ABC 中，若a ＝2，b ＝3A ＝30°，则B ＝（ ） A ．60° B ．60°或 120°C ．30°D ．30°或150°【答案】B【解析】根据正弦定理直接求出sin B ，即可求出角B . 【详解】由正弦定理可得sin B ＝ bsin A a ＝23sin 30︒⨯＝3. 因为0＜B ＜180°，所以B ＝60°或 120°， 故选：B 【点睛】本题主要考查了正弦定理解三角形，属于容易题.8．如图，第（1）个图案由1个点组成，第（2）个图案由3个点组成，第（3）个图案由7个点组成，第（4）个图案由13个点组成，第（5）个图案由21个点组成，⋅⋅⋅，依次类推，根据图案中点的排列规律，第50个图形由多少个点组成（ ）A ．2449B ．2451C ．2455D ．2458【答案】B【解析】设第()n 个图案的点的个数为n a ，推测得到12(1)n n a a n --=-，利用1n -个式子相加，由等差数列的求和公式，即可求解. 【详解】设第()n 个图案的点的个数为n a ，由题意可得123451,3,7,13,21,a a a a a =====， 可得213243542,4,6,8,a a a a a a a a -=-=-=-=，由此推测12(1)n n a a n --=-，则()()()()21324312462(1)n n a a a a a a a a n --+-+-+-=++++-，化简可得(1)(222)1(1)2n n n a n n -+--==-，所以(1)1n a n n =-+所以5050(501)12451a =⨯-+=. 故选：B. 【点睛】本题主要考查了归纳推理的应用，其中解答中构造数列并得出的数列的递推关系式，结合等差数列的求和公式求解是解答的关键，着重考查推理与运算能力.9．如图，AD 是某防汛抗洪大坝的坡面，大坝上有一高为20米的监测塔BD ，若某科研小组在坝底A 点测得15BAD ∠=，沿着坡面前进40米到达E 点，测得45BED ∠=，则大坝的坡角（DAC ∠）的余弦值为（ ）A ．31B ．312C 21D ．212【答案】A【解析】由15BAD ∠=，45BED ∠=，可得30ABE ∠=，在ABE ∆中，由正弦定理得(2062BE =，在BED ∆中，由正弦定理得sin 31BDE ∠=，进而由()sin sin 90BDE DAC ∠=∠+可得结果.【详解】因为15BAD ∠=，45BED ∠=，所以30ABE ∠=.在ABE ∆中，由正弦定理得sin 30sin15AE BE=，解得2062BE =.在BED ∆中，由正弦定理得sin sin 45BE BDBDE =∠，所以220622sin 3120BDE ∠==.又90ACD ∠=，所以()sin sin 90BDE DAC ∠=∠+，所以cos31DAC ∠=-. 故选A . 【点睛】本题考查正弦定理解三角形，考查诱导公式，考查学生合理进行边角转化的能力，属于中档题.10．如图，已知ABC 面积为4，连接ABC 三边的中点构成第二个三角形，再连接第二个三角形三边中点构成第三个三角形，依此类推，第2020个三角形面积为（ ）A ．201714B ．201814C ．201914D ．202014【答案】B【解析】可知后一个三角形的面积是前一个的14，则这些三角形的面积形成一个等比数列，求出第2020项即可. 【详解】观察图形可知后一个三角形的面积是前一个的14， 设第n 个三角形的面积为n a ， 则数列{}n a 是首项为14a =，公比为14的等比数列， 1211444n n n a --⎛⎫⎛⎫∴=⨯= ⎪⎪⎝⎭⎝⎭，∴第2020个三角形面积为2018202020181144a ⎛⎫==⎪⎝⎭.故选：B. 【点睛】本题考查等比数列的应用，属于基础题.11．已知数列{}n a 是等差数列，若91130a a +<，10110a a ⋅<，且数列{}n a 的前n 项和n S 有最大值，那么n S 取得最小正值时n 等于（ ） A ．1 B ．20C ．10D ．19【答案】D【解析】根据已知条件，判断出1011,a a 的符号，再根据等差数列前n 项和的计算公式，即可求得. 【详解】因为等差数列的前n 项和有最大值，故可得0d < 因为91130a a +<，故可得91011120a a a a +++<， 整理得()101120a a +<，即10110a a +<， 又因为10110a a ⋅<， 故可得10110,0a a ><.又因为1910190S a =>，()201011100S a a =+<， 故n S 取得最小正值时n 等于19. 故选：D . 【点睛】本题考查等差数列的性质，以及前n 项和的性质，属综合中档题. 12．设a ，b ，c 分别是ABC 内角A ，B ，C 的对边，若1tan A ，1tan B ，1tan C依次成公差不为0的等差数列，则（ ） A ．a ，b ，c 依次成等差数列 B ．2a ，2b ，2c 依次成等差数列C ，依次成等比数列D ．2a ，2b ，2c 依次成等比数列【答案】B【解析】由等差数列的性质得tan ta t 221n an B A C=+，利用正弦定理、余弦定理推导出2222a c b +=，从而2a ，2b ，2c 依次成等差数列. 【详解】解：∵a ，b ，c 分别是ABC 内角A ，B ，C 的对边，1tan A ，1tan B ，1tan C依次成公差不为0的等差数列，∴211 tan tan tanB A C=+，根据正弦定理可得cos cos cos2b aCcB A=+，∴2cos cosac B bc A abcsC=+，∴22222222222b c a a b ca c b+-+-+-=+，∴2222a c b+=，∴2a，2b，2c依次成等差数列.故选：B.【点睛】本题考查三个数成等差数列或等比数列的判断，考查等差数列、等比数列的性质、正弦定理、余弦定理等基础知识，考查运算求解能力，考查函数与方程思想，属于中档题.二、填空题13．若实数,x y满足4360x yx yy+≥⎧⎪+-≤⎨⎪≥⎩，则z x y=-的最小值是_________.【答案】2【解析】画出可行域和目标函数，根据目标函数的几何意义得到最值.【详解】如图所示，画出不等式组表示的平面区域，可知不等式组表示的平面区域为三角形ABC所在区域，其中()()()4,0,3,1,6,0A B C，z x y =-可转化为直线y x z =-，可知当直线过B 时，z 取得最小值为2.故答案为：2 【点睛】本题考查了线性规划问题，画出图象是解题的关键.14．某小组有2名男生和3名女生，从中任选2名同学参加演讲比赛，那么至多一名女生参加的概率为___________. 【答案】710【解析】将2名男生和3名女生进行标记，列出基本事件个数，再古典概型的概率计算公式即可求解. 【详解】将2名男生标记为,A B ，3名女生标记为1,2,3， 从中任选2名同学：()()()()()()(),,,1,,2,,3,,1,,2,,3,A B A A A B B B()()()1,2,1,3,2,3，共10个基本事件，至多一名女生：()()()()()()(),,,1,,2,,3,,1,,2,,3,A B A A A B B B 共7个基本事件.所以至多一名女生参加的概率为710p =. 故答案为：710【点睛】本题考查了古典概型的概率计算公式、列举法求基本事件个数，属于基础题.15．已知()()9132xxf x k =-+⋅+，当x ∈R 时，()f x 恒为正值，则实数k 的取值范围是________.【答案】(),1-∞【解析】利用换元法，将指数函数转化为二次函数，即可求k 的取值范围. 【详解】解：令()30xt t =>，则()()212g t t k t =-++，若x ∈R 时，()f x 恒为正值，则()()2120g t t k t =-++>对0t >恒成立，∴()2102180k k +⎧>⎪⎨⎪+-<⎩①，或()102020k g +⎧≤⎪⎨⎪=>⎩②，解①得11k -<<，解②得1k ≤-.综上所述，1k <，即实数k的取值范围为()1k ∈-∞.故答案为：(),1-∞. 【点睛】本题主要考查不等式恒成立问题，考查指数函数的性质及转化思想，属于中档题．16．已知正项数列{}n a 的前n 项和为n S ，且满足112n n n S a a ⎛⎫=+ ⎪⎝⎭，则1264111S S S ⎡⎤++⋅⋅⋅+=⎢⎥⎣⎦______（其中[]x 表示不超过x 的最大整数）. 【答案】14【解析】首先通过1n n n a S S -=-，代入整理可得2211n n S S --=，所以{}2n S 是以1为首项，1为公比的等差数列，再通过放缩和裂项相消法，即可得到126411111141)1)15S S S S <<+++<+=，即可得解. 【详解】当2n ≥时，1n n n a S S -=-， 则1111()2n n n n n S S S S S --=-+-， 整理可得：111n n n n S S S S --+=-，即：2211n n S S --=， 当1n =时，111111()2S a a a ==+， 解得11a =，则11S =， 所以{}2nS 是以1为首项，1为公差的等差数列，则21(1),n S n n n N *=+-=∈ ，所以,n S n n N *=∈，因为11212nn n S n n n +-=<=++故当2n ≥时，1==1221n n n S n n nn n <=--+--所以12(1)nn n S <--， 所以12(1)2(1)nn n n n S +-<<--， 则126411111142(651)2(641)15S S S S <-<+++<+-=， 则1264111=15S S S ⎡⎤+++⎢⎥⎣⎦. 故答案为：14. 【点睛】本题考查了利用n a 和n S 的关系求得通项公式，考查了裂项相消法和放缩法求范围，整体计算量比较大，属于难题.三、解答题17．已知一个几何体的三视图如图所示.（1）求此几何体的表面积；（2）如果点P ，Q 在正视图中所示位置，P 为所在线段中点，Q 为顶点，求在几何体侧面的表面上，从P 点到Q 点的最短路径的长. 【答案】（1）)225S a π=表；（2）21a π+【解析】（1）由三视图知：此几何体是一个圆锥和一个圆柱的组合体，底面圆半径长a ，圆柱高为2a ，圆锥高为a ．（2）将圆柱侧面展开，在平面矩形内线段PQ 长为所求． 【详解】（1）由三视图知该几何体是由一个圆锥与一个圆柱组成的组合体，其表面积是圆锥的侧面积、圆柱的侧面积和圆柱的一个底面积之和.()()212222S a a a ππ=⋅=圆锥侧，()()2224S a a a ππ=⋅=圆柱侧，2S a π=圆柱底，所以()22222425S a a a a ππππ=++=+表.（2）沿P 点与Q 点所在母线剪开圆柱侧面，如图.则()2222PQ AP AQ a a π=+=+21a π=+，所以从P 点到Q 点在侧面上的最短路径的长为21a π+. 【点睛】本题考查由三视图求面积，解题的关键是由三视图还原出实物图的几何特征及其度量，再由公式求出表面积，还考查曲面距离最值问题，采用化曲面为平面的办法．须具有空间想象能力、转化、计算能力．18．某电讯企业为了了解某地区居民对电讯服务质量评价情况，随机调查100 名用户，根据这100名用户对该电讯企业的评分，绘制频率分布直方图，如图所示，其中样本数据分组为[)40,50，[)50,60，……[90,100].（1）估计该地区用户对该电讯企业评分不低于70分的概率，并估计对该电讯企业评分的中位数；（结果保留两位有效数字）（2）现从评分在[)40,60的调查用户中随机抽取2人，求2人评分都在[)40,50的概率. 【答案】（1）概率为0.70，中位数为77.14；（2）215. 【解析】（1）由题意列出频率分布表，求和即可估计该地区用户对该电讯企业评分不低于70分的概率；利用中位数两侧的概率和相等列方程即可估计对该电讯企业评分的中位数；（2）由题意计算出受调查用户评分在[40,50)、[40,60)的人数，求出总的基本事件个数及满足要求的基本事件的个数，由古典概型概率公式即可得解. 【详解】（1）由题意，该地区用户对该电讯企业评分频率分布如下表：因此可估计评分不低于70分的概率为0.280.240.180.70P =++=； 对该电讯企业评分的中位数设为x ，可得7080x <<， 则700040060200.280.5010x .+.+.+-⨯=， 解得77.14x ≈，所以可估计对该电讯企业评分的中位数为77.14； （2）受调查用户评分在[40,50)的有1000.04=4⨯人，若编号依次为1，2，3，4，从中选2人的事件有{}1,2、{}1,3、{}1,4、{}2,3、{}2,4、{}3,4，共有3216++=个基本事件；受调查用户评分在[40,60)的有()1000.040.06=10⨯+人，若编号依次为1，2，3，..9，10，从中选2人，可得共有9198719452++++⋅⋅⋅+=⨯=个基本事件；因此2人评分都在[40,50)的概率624515P ==. 【点睛】本题考查了频率分布直方图的应用，考查了古典概型概率的求解与运算求解能力，属于中档题.19．设函数()()21f x x m x m =-++.（1）求不等式()0f x <的解集；（2）若对于[]1,2x ∈，()4f x m >-恒成立，求m 的取值范围. 【答案】（1）见解析；（2）(),3-∞.【解析】（1）由()0f x <得()()10x m x --<，然后分1m <、1m =、1m 三种情况来解不等式()0f x <；（2）由()4f x m >-恒成立，由参变量分离法得出41m x x<+-，并利用基本不等式求出41x x+-在[]1,2上的最小值，即可得出实数m 的取值范围. 【详解】 （1）()0f x <，()210x m x m ∴-++<，()()10x m x ∴--<.当1m <时，不等式()0f x <的解集为(),1m ；当1m =时，原不等式为()210x -<，该不等式的解集为∅； 当1m 时，不等式()0f x <的解集为()1,m ；（2）由题意，当[]1,2x ∈时，()2140x m x -++>恒成立，即[]1,2x ∈时，41m x x<+-恒成立.由基本不等式得4113x x +-≥=，当且仅当[]21,2x =∈时，等号成立， 所以，3m <，因此，实数m 的取值范围是(),3-∞. 【点睛】本题考查含参二次不等式的解法，同时也考查了利用二次不等式恒成立求参数的取值范围，在含单参数的二次不等式恒成立问题时，可充分利用参变量分离法，转化为函数的最值来求解，可避免分类讨论，考查化归与转化思想的应用，属于中等题.20．改革开放以来，人们的支付方式发生了巨大转变．近年来，移动支付已成为主要支付方式之一．为了解某校学生上个月A ，B 两种移动支付方式的使用情况，从全校所有的1000名学生中随机抽取了100人，发现样本中A ，B 两种支付方式都不使用的有5人，样本中仅使用A 和仅使用B 的学生的支付金额分布情况如下：支付金额支付方式不大于2000元大于2000元仅使用A27人3人仅使用B24人1人（Ⅰ）估计该校学生中上个月A，B两种支付方式都使用的人数；（Ⅱ）从样本仅使用B的学生中随机抽取1人，求该学生上个月支付金额大于2000元的概率；（Ⅲ）已知上个月样本学生的支付方式在本月没有变化．现从样本仅使用B的学生中随机抽查1人，发现他本月的支付金额大于2000元．结合（Ⅱ）的结果，能否认为样本仅使用B的学生中本月支付金额大于2000元的人数有变化？说明理由．【答案】（Ⅰ）400人；（Ⅱ）1 25；（Ⅲ）见解析.【解析】(Ⅰ)由题意利用频率近似概率可得满足题意的人数；(Ⅱ)利用古典概型计算公式可得上个月支付金额大于2000元的概率；(Ⅲ)结合概率统计相关定义给出结论即可.【详解】（Ⅰ）由图表可知仅使用A的人数有30人，仅使用B的人数有25人，由题意知A,B两种支付方式都不使用的有5人，所以样本中两种支付方式都使用的有1003025540---=，所以全校学生中两种支付方式都使用的有401000400100⨯=（人）.（Ⅱ）因为样本中仅使用B的学生共有25人，只有1人支付金额大于2000元，所以该学生上个月支付金额大于2000元的概率为1 25.（Ⅲ）由（Ⅱ）知支付金额大于2000元的概率为1 25，因为从仅使用B的学生中随机调查1人，发现他本月的支付金额大于2000元，依据小概率事件它在一次试验中是几乎不可能发生的，所以可以认为仅使用B的学生中本月支付金额大于2000元的人数有变化，且比上个月多. 【点睛】本题主要考查古典概型概率公式及其应用，概率的定义与应用等知识，意在考查学生的转化能力和计算求解能力.21．ABC 中，角A ，B ，C 所对的边分别为,,a b c .已知3,cos 2a A B A π===+. （1）求b 的值； （2）求ABC 的面积. 【答案】（1）（2）2. 【解析】（1）根据cos 3A =求出sin A ，根据2B A π=+求出sin B ，根据正弦定理求出b ；（2）先求出sin C ，再利用面积公式即可求出. 【详解】（1）在ABC中，由题意知sin A ==， 又因为2B A π=+，所有sin sin()cos 23B A A π=+==，由正弦定理可得3sin sin 3a BAb ===. （2）由2B A π=+得cos cos sin 2(3)B A A π=+=-=-，由A B C π++=,得()C A B π=-+.所以sin sin[()]sin()C A B A B π=-+=+sin cos cos sin A B A B =+()3333=-+⨯13=. 因此，ABC的面积111sin 32232S ab C ==⨯⨯=.【点睛】本题考查正弦定理和三角形面积公式的应用，属于中档题. 22．在等比数列{}n a 中,()*10a n N >∈,且328aa -=,又15,a a 的等比中项为16.（1）求数列{}n a 的通项公式:（2）设4log n n b a =,数列{}n b 的前n 项和为n S ,是否存在正整数k ,使得1231111nk S S S S ++++<对任意*n N ∈恒成立.若存在,求出正整数k 的最小值;若不存在,请说明理由.【答案】（1）12n n a +=（2）3.【解析】试题分析：（1）由题意可得316a =，又328a a -=，故28a =，由此可得等比数列的公比2q =，因此可得12n n a +=．（2）由（1）得12n n b +=，所以()34n n n S +=，从而()14411333n S n n n n ⎛⎫==- ⎪++⎝⎭，求和可得123111141111141122113231233239n S S S S n n n ⎛⎫⎛⎫++++=⨯++---<⨯++= ⎪ ⎪+++⎝⎭⎝⎭，所以可得229k ≥，故存在满足题意得k ，且k 的最小值为3． 试题解析：（1）设等比数列{}n a 的公比为q ， ∵15a a ，的等比中项为16． ∴316a =， 又328a a -=，28a ∴=，∴322a q a ==， ∴21822n n n a -+=⨯==．（2）由（1）得141log 22n n n b ++==， ∴数列{}n b 为等差数列，且11b =．∴()113224n n n n n S +⎛⎫+ ⎪+⎝⎭==， ∴()14411333n S n n n n ⎛⎫==- ⎪++⎝⎭， ∴123111141111111131425363n S S S S n n ⎛⎫++++=⨯-+-+-++- ⎪+⎝⎭4111111323123n n n ⎛⎫=⨯++--- ⎪+++⎝⎭ 4112213239⎛⎫<⨯++= ⎪⎝⎭， ∴229k ≥， ∴存在满足题意得k ，且k 的最小值为3． 点睛：用裂项法求和的原则及规律（1）裂项原则：一般是前边裂几项，后边就裂几项，直到发现被消去项的规律为止． （2）消项规律：消项后前边剩几项，后边就剩几项，前边剩第几项，后边就剩倒数第几项，消项后的剩余部分具有对称性．。

2019-2020学年吉林省长春北师大附校高一（下）期末数学试卷一、单选题（本大题共12小题，共60.0分）1.直线√3x+y+1=0的倾斜角为()A. π3B. 2π3C. π6D. 5π62.过点(0,2)且与直线x−y=0垂直的直线方程为()A. x+y−2=0B. x−y−2=0C. x+y+2=0D. x−y+2=03.已知直线a，b，平面α，且a⊥α，下列条件中能推出a//b的是()A. b//αB. b⊂αC. b⊥αD. b与α相交4.在△ABC中，内角A，B，C所对的边分别是a，b，c.已知A=45°，a=6，b=3√2，则B的大小为()A. 30°B. 60°C. 30°或150°D. 60°或120°5.如果a>b>0，c>d>0，则下列不等式中不正确的是()A. a−d>b−cB. ad >bcC. a+d>b+cD. ac>bd6.已知数列{b n}是等比数列，b9是1和3的等差中项，则b2b16=()A. 16B. 8C. 2D. 47.如图，网格纸上小正方形的边长为1，粗线画出的是某几何体的三视图，则此几何体的体积为()A. 6B. 9C. 12D. 188.若直线l1:ax+2y−4=0与l2:x+(a+1)y+2=0平行，则实数a的值为()A. 或a=1B. a=1C. D.9.《张丘建算经》是我国南北朝时期的一部重要数学著作，书中系统的介绍了等差数列，同类结果在三百多年后的印度才首次出现.书中有这样一个问题，大意为：某女子善于织布，后一天比前一天织得快，而且每天增加的数量相同，已知第一天织布5 尺，一个月(按30天计算)总共织布390 尺，问每天增加的数量为多少尺？该问题的答案为()A. 829尺 B. 1629尺 C. 3229尺 D. 12尺10.△ABC中，角A，B，C的对边分别为a，b，c，且A=60°，b=1，c=4，则△ABC外接圆的半径为()A. √39B. √393C. √396D. 2√39311.底面是正方形，从顶点向底面作垂线，垂足是底面中心的四棱锥称为正四棱锥．如图，在正四棱锥P−ABCD中，底面边长为1.侧棱长为2，E为PC的中点，则异面直线PA与BE所成角的余弦值为()A. √33B. √63C. √22D. 1212.已知x>0，y>0，且x+2y=1，若不等式2x +1y≥m2+7m恒成立，则实数m的取值范围是()A. −8≤m≤1B. m≤−8或m≥1C. −1≤m≤8D. m≤−1或m≥8二、单空题（本大题共4小题，共20.0分）13.设变量x、y满足约束条件{x+y≤1x−2y≤0x≥−1，则目标函数z=x+2y的最大值为______．14.两平行直线x+3y−4=0与2x+6y−9=0的距离是______．15.已知1，x1，x2，7成等差数列，1，y1，y2，8成等比数列，设点M(x1,y1)，N(x2,y2)，则直线MN的方程是______．16.在正方体ABCD−A1B1C1D1中，下面结论正确的是______．①BD//平面CB1D1；②AC1⊥BD；③AC1⊥平面CB1D1；④异面直线AD与CB1所成的角为60°．三、解答题（本大题共6小题，共70.0分）17.已知三角形的三个顶点A(−2,0)，B(4,−4)，C(0,2)，(1)求线段BC的中线所在直线方程；(2)求过点AB边上的高所在的直线方程．18.如图，正方形ABCD−A1B1C1D1的棱长为2，E，F分别为A1B，AC的中点．(1)证明：EF//平面A1C1D；(2)求三棱锥F−A1C1D的体积．19.△ABC中，角A，B，C的对边分别为a，b，c，且sin2A+sin2C−√3sinAsinC=sin2B.(1)求角B的大小；(2)若a=√3，b=1，求△ABC的面积．20.某地计划建造一间背面靠墙的小屋，其地面面积为12m2，墙面的高度为3m，经测算，屋顶的造价为5800元，房屋正面每平方米的造价为1200元，房屋侧面每平方米的造价为800元．设房屋正面地面长方形的边长为xm，房屋背面和地面的费用不计．(1)用含x的表达式表示出房屋的总造价z；(2)怎样设计房屋能使总造价最低？最低造价是多少？21.已知等差数列{a n}的公差不为零，前n项和为S n，若S8=64，且a1，a2，a5成等比数列．(1)求数列{a n}的通项公式；(2)设b n=a n，数列{b n}的前n项和T n.求证：T n<3．2n22.如图，四棱锥P−ABCD中，PA⊥平面ABCD，PA=AD=2.四边形ABCD满足BC//AD，AB⊥AD，AB=BC=1.F为侧棱PC上的任意一点．(1)求直线PC与平面ABCD所成角的余弦值；(2)求证：平面AFD⊥平面PAB；(3)是否存在点F，使得直线AF与平面PCD垂直？若存在，请说明理由并求出线段PF的长；若不存在，请说明理由．答案和解析1.【答案】B【解析】解：直线√3x+y+1=0的斜率等于−√3，设它的倾斜角等于θ，则0≤θ<π，且tanθ=−√3，∴θ=2π，3故选：B．直线的斜率等于−√3，设它的倾斜角等于θ，则0≤θ<π，且tanθ=−√3，求得θ值，即为所求．本题考查直线的倾斜角和斜率的关系，以及倾斜角的取值范围，已知三角函数值求角的大小，得到tanθ=−√3，是解题的关键．2.【答案】A【解析】解：根据题意，要求直线与与直线x−y=0垂直，设要求直线的方程为x+y−a=0，又由要求直线经过点(0,2)，则有0+2−a=0，解可得a=2；故要求直线的方程为x+y−2=0；故选：A．根据题意，设要求直线的方程为x+y−a=0，将点(0,2)的坐标代入计算可得a的值，即可得答案．本题考查直线垂直的判断，涉及直线的一般式方程，属于基础题．3.【答案】C【解析】解：A中，若b//α，由a⊥α，可得a⃗⊥b⃗ ；故A不满足题意；B中，若b⊂α，由a⊥α，可得a⃗⊥b⃗ ；故B不满足题意；C中，若b⊥α，由a⊥α，可得a//b；故C正确；D中，若b与α相交，由a⊥α，可得a，b异面或平，故D不满足题意．故选：C．根据线面垂直的性质，逐项判断即可得出结果．本题主要考查线面垂直的性质，熟记线面垂直的性质定理即可，属于常考题型．4.【答案】A【解析】解：在△ABC中，由正弦定理可得asinA =bsinB，即6sin45∘=3√2sinB，解得sinB=12．∵b<a，∴B<A=45°，∴B=30°，故选A．由正弦定理求得sinB=12，再由大边对大角求得B的值．本题主要考查正弦定理的应用，大边对大角，已知三角函数值求角的大小，属于中档题．5.【答案】C【解析】解：A：a>b>0，c>d>0得：a−d>b−c，正确B中，a>b>0，c>d>0得1d >1c：两边同乘得ad>bc，正确．C中，若a=3，b=2，c=1，d=0时，错误；D中，中a>b>0，c>d>0两边同乘，不等号方向不变，正确；故选：C．这考查有关不等式的四则运算的知识，由不等式的性质直接判断即可．本题考查不等式的性质，属基础知识的考查．做此题要考虑全面，特别要注意“正数”这个条件．6.【答案】D【解析】【分析】本题考查了等差数列与等比数列的通项公式及其性质，考查了推理能力与计算能力，属于基础题．利用等差数列与等比数列的通项公式及其性质即可得出．【解答】解：∵b 9是1和3的等差中项，∴2b 9=1+3，∴b 9=2，由等比数列{b n }的性质可得：b 2b 16=b 92=4，故选D ．7.【答案】B【解析】解：该几何体是三棱锥，底面是俯视图，三棱锥的高为3； 底面三角形斜边长为6，高为3的等腰直角三角形， 此几何体的体积为V =13×12×6×3×3=9． 故选：B ．通过三视图判断几何体的特征，利用三视图的数据求出几何体的体积即可． 本题考查三视图与几何体的关系，考查几何体的体积的求法，考查计算能力．8.【答案】B【解析】解：∵直线l 1:ax +2y −4=0与l 2:x +(a +1)y +2=0平行， ∴{a(a +1)−2=02a +4≠0，解得a =1．故选：B ．由两直线A 1x +B 1y +C 1=0与A 2x +B 2y +C 2=0平行，可得{A 1B 2−A 2B 1=0A 1C 2−A 2C 1≠0，由此列式求解a 值．本题考查直线的一般式方程与直线平行的关系，是基础题．9.【答案】B【解析】解：由题意，该女子从第一天起，每天所织的布的长度(单位：尺)成等差数列， 记为：a 1，a 2，a 3，…，a n ，其公差为d ， 则a 1=5，S 30=390， ∴30a 1+30×292d =390，∴d =1629． 故选：B ．本题主要考查等差数列求和的应用，是基础题．由题意该女子从第一天起，每天所织的布的长度(单位：尺)成等差数列，记公差为d ，由等差数列的前n 项和公式求解即可．10.【答案】B【解析】解：由余弦定理可得：a 2=b 2+c 2−2bccosA =13，可得：a =√13， 设△ABC 外接圆的半径为R ，则由正弦定理可得：2R =a sinA=√13sin60°=2√393， 解得△ABC 外接圆的半径为R =√393．故选：B ．由已知及余弦定理可求a 的值，再由正弦定理计算可得．本题主要考查了余弦定理，正弦定理在解三角形中的应用，考查了转化思想，属于基础题．11.【答案】B【解析】解：连接AC ，BD ，设AC ∩BD =O ，连接EO ，则EO//PA ，∴∠BEO 为异面直线PA 与BE 所成角， 连接PO ，可得PO ⊥底面ABCD ，则PO ⊥BD ， 又AC ⊥BD ，PO ∩AC =O ， ∴BD ⊥平面PAC ，则BD ⊥OE ． ∵底面边长为1，∴OB =√22，∵侧棱长为2，∴OE =1，在Rt △BOE 中，求得BE =√12+(√22)2=√62．∴cos∠BOE =1√62=√63．即异面直线PA 与BE 所成角的余弦值为√63．故选：B ．连接AC ，BD ，设AC ∩BD =O ，连接EO ，则EO//PA ，可得∠BEO 为异面直线PA 与BE 所成角，证明BD ⊥平面OAC ，则BD ⊥OE ，然后求异面直线PA 与BE 所成角的余弦值即可．本题考查异面直线所成角的求法，考查空间想象能力与思维能力，是基础题．12.【答案】A【解析】解：∵x >0，y >0，x +2y =1， ∴2x +1y =(x +2y)(2x +1y )=4 y x+x y +4≥4+2√4=8.(当4 y x=x y ，即x =2y =12时取等号)，∵不等式2x +1y ≥m 2+7m 成立， ∴m 2+7m ≤8， 求得−8≤m ≤1． 故选：A ．由题意可得2x +1y =(x +2y)(2x +1y )=4 y x+x y+4≥4+2√4=8，不等式2x+1y≥m 2+7m 成立⇔m 2+7m <(2x +1y )min ，即可求得实数m 的取值范围．本题主要考查了基本不等式在最值问题中的应用，考查了学生分析问题和解决问题的能力，属于中档题．13.【答案】3【解析】解：由变量x 、y 满足约束条件{x +y ≤1x −2y ≤0x ≥−1，作出可行域如图，联立{x =−1x +y =1，解得A(−1,2)，化目标函数z =x +2y 为y =−x2+z2． 由图可知，当直线y =−x2+z 2过A 时，直线在y 轴上的截距最大，z 有最大值为：3． 故答案为：3．利用约束条件作出可行域，化目标函数为直线方程的斜截式，数形结合得到最优解，联立方程组求得最优解的坐标，代入目标函数得答案．本题考查简单的线性规划，考查了数形结合的解题思想方法，是中档题．14.【答案】√1020【解析】解：由直线x+3y−4=0取一点A，令y=0得到x=4，即A(4,0)，则两平行直线的距离等于A到直线2x+6y−9=0的距离d=|8−9|√22+62=12√10=√1020．故答案为：√1020在一条直线上任取一点，求出这点到另一条直线的距离即为两平行线的距离．此题是一道基础题，要求学生理解两条平行线的距离的定义．会灵活运用点到直线的距离公式化简求值．15.【答案】x−y−1=0【解析】解：由1，x1，x2，7成等差数列，得d=7−14−1=2，∴x1=3，x2=5；由1，y1，y2，8成等比数列，得q=√813=2，∴y1=2，y2=4．∴点M(x1,y1)=(3,2)，N(x2,y2)=(5,4)，则直线MN的方程是：y−24−2=x−35−3，即x−y−1=0．故答案为：x−y−1=0．由已知分别求出等差数列的公差与等比数列的公比，再分别求出M，N的坐标，代入直线方程的两点式得答案．本题考查等差数列与等比数列的通项公式，考查了直线的两点式方程，是基础题．16.【答案】①②③【解析】解：在正方体ABCD−A1B1C1D1中，在①中，∵BD//B1D1，且BD⊄平面CB1D1，B1D1⊂平面CB1D1，∴BD//平面CB1D1，故①正确；又AC∩CC1=C，∴BD⊥平面ACC1，∵AC1⊂平面ACC1，∴AC1⊥BD，故②正确；在③中，∵B1D1⊥A1C1，B1D1⊥AA1，且AA1∩A1C1=A1，∴B1D1⊥平面AA1C1，又AC1⊂平面AA1C1，∴B1D1⊥AC1，同理，B1C⊥AC1，又B1D1∩B1C=B1，∴AC1⊥平面CB1D1，故③正确；在④中，∵AD//BC，∴∠BCB1是异面直线AD与CB1所成的角，∵BB1⊥BC，且BB1=BC，∴∠BCB1=45°，∴异面直线AD与CB1所成的角为45°，故④错误．故答案为：①②③．在①中，由BD//B1D1，得到BD//平面CB1D1；在②中，由BD⊥AC，BD⊥CC1，得到BD⊥平面ACC1，从而AC1⊥BD；在③中，由B1D1⊥AC1，B1C⊥AC1，得到AC1⊥平面CB1D1；在④中，异面直线AD与CB1所成的角为45°．本题考查命题真假的判断，考查空间中线线、线面、面面间的位置关系等基础知识，考查运算求解能力，考查函数与方程思想，是中档题．17.【答案】解：(1)线段BC的中点M(2,−1)，∴线段BC的中线所在直线方程为；y−0=−1−02−(−2)(x+2)，即x+4y+2=0．(2)k AB=−4−04−(−2)=−23．∴过点AB边上的高所在的直线方程为：y=32x+2，即3x−2y+4=0．【解析】(1)线段BC的中点M(2,−1)，利用点斜式即可得出．(2)利用斜率计算公式可得k AB，利用相互垂直的直线斜率之间的关系可得过点AB边上的高所在的直线的斜率，利用斜截式即可得出．本题考查了直线的点斜式、斜截式、斜率计算公式、相互垂直的直线斜率之间的关系，考查了推理能力与计算能力，属于基础题．18.【答案】解：(1)证明：连结BD，∵E、F分别为AB，BD的中点，∴EF//A1D，∵EF⊄面A1C1D，A1D⊂面A1C1D，∴EF//面A1C1D.∴FD⊥平面ACC1A1，∴三棱锥F−A1C1D的体积：V F−A1C1D =V D−A1C1F=13⋅12⋅2√2⋅2√2=43．【解析】(1)连结BD，推导出EF//A1D，由此能证明EF//面A1C1D.(2)由FD⊥AC，FD⊥CC1，得FD⊥平面ACC1A1，由此能求出三棱锥F−A1C1D的体积．本题考查线面平行的证明，考查三棱锥的体积的求法，考查空间中线线、线面、面面间的位置关系等基础知识，考查运算求解能力，是中档题．19.【答案】解：(1)因为sin2A+sin2C−√3sinAsinC=sin2B，所以由正弦定理可得a2+c2−√3ac=b2．由余弦定理可得cosB=a2+c2−b22ac =√3ac2ac=√32，因为B∈(0,π)，所以B=π6．(2)因为B=π6，a=√3，b=1，所以由余弦定理b2=a2+c2−2accosB，可得1=3+c2−2×√3×c×√32，整理可得c2−3c+2=0，解得c=2，或1，所以S△ABC=12acsinB=√32，或√34．【解析】(1)由正弦定理可得a2+c2−√3ac=b2，由余弦定理可得cosB=√32，结合范围B∈(0,π)，可得B的值．(2)由已知利用余弦定理可得c2−3c+2=0，解方程可得c的值，进而根据三角形的面积公式即可求解．本题主要考查了正弦定理，余弦定理以及三角形的面积公式在解三角形中的应用，考查了转化思想和方程思想的应用，属于基础题．20.【答案】解：(1)设总造价为z元，则由xy=12，可得y=12，∴z=3y×1200+6x×800+5800=12×3600x+4800x+5800，(x>0)；(2)z≥2√12×3600x⋅4800x+5800=34600，当12×3600x=4800x时，即x=3时，z有最小值34600，此时y=4．答：长4m，宽3m.最低总造价为34600元．【解析】(1)由已知中地面面积为12m2，我们可得xy=12，可得y=12x，根据房屋正面每平方米的造价为1200元，房屋侧面每平方米的造价为800元，屋顶的造价共5200元．根据墙高为3m，我们可以构造房屋总造价的函数解析式；(2)利用基本不等式即可求出函数的最小值，注意等号成立的条件，进而得到答案．本题考查的知识点是函数模型的选择与应用，函数的值域，其中根据已知条件构造房屋总造价的函数解析式，将实际问题转化为函数的最值问题，运用基本不等式是解答本题的关键．21.【答案】解：(1)设等差数列{a n}的公差为d，d不为零，由S8=64，且a1，a2，a5成等比数列，可得8a1+28d=64，且a22=a1a5，即(a1+d)2=a1(a1+4d)，解得a1=1，d=2，则a n=1+2(n−1)=2n−1；(2)证明：b n=a n2n =2n−12n，T n=12+34+58+...+2n−12n，1 2T n=14+38+516+...+2n−32n+2n−12n，上面两式相减可得12T n=12+12+14+...+12n−1−2n−12n+1=12+12(1−12n−1)1−12−2n−12n+1=32−2n+32n+1，所以T n=3−2n+32n，由2n+32n>0，可得T n<3．【解析】(1)设等差数列{a n }的公差为d ，d 不为零，由等差数列的通项公式和求和公式、等比数列的中项性质，解方程可得首项和公差，可得所求；(2)求得b n =a n2n=2n−12n，由数列的错位相减法，结合等比数列的求和公式，以及不等式的性质，即可得证．本题考查等差数列和等比数列的通项公式和求和公式的运用，以及数列的错位相减法，考查方程思想和运算能力，属于中档题．22.【答案】解：(1)∵PA ⊥平面ABCD ，PA =AD =2.四边形ABCD 满足BC//AD ，AB ⊥AD ，AB =BC =1，∴以A 为原点，AB 为x 轴，AD 为y 轴，AP 为z 轴，建立空间直角坐标系， 则平面ABCD 的法向量n⃗ =(0,0，1)， P(0,0，2)，C(1,1，0)，PC ⃗⃗⃗⃗⃗ =(1,1，−2)， 设直线PC 与平面ABCD 所成角为θ， 则sinθ=|PC ⃗⃗⃗⃗⃗ ⋅n ⃗⃗ ||PC ⃗⃗⃗⃗⃗ |⋅|n ⃗⃗ |=√6=√63， ∴直线PC 与平面ABCD 所成角的余弦值为√1−(√63)2=√33．(2)证明：∵PA ⊥平面ABCD ，又AD ⊂平面ABCD ，∴PA ⊥AD ． 又∵AB ⊥AD ，PA ∩AB =A ，∴AD ⊥平面PAB ， 而AD ⊂平面AFD ，∴平面AFD ⊥平面PAB ． (3)在棱PC 上存在点F 使得AF ⊥PC ．由已知，AB ⊥AD ，BC//AD ，AB =BC =1，AD =2． 由平面几何知识可得CD ⊥AC ．由(2)知，PA ⊥平面ABCD ，∴PA ⊥CD ， ∵PA ∩AC =A ，∴CD ⊥平面PAC ． 而AF ⊂平面PAC ，∴CD ⊥AF ．又因为CD ∩PC =C ，所以AF ⊥平面PCD ． 在△PAC 中，PA =2，AC =√2，∠PAC =90°， 解得，PC =√6，PF =2√63． ∴直线AF 与平面PCD 能够垂直，此时线段PF 的长为2√63．【解析】(1)以A为原点，AB为x轴，AD为y轴，AP为z轴，建立空间直角坐标系，利用向量法能求出直线PC与平面ABCD所成角的余弦值(2)推导出AD⊥平面PAB，利用面面垂直的判定，可得AD⊂平面AFD，所以平面AFD⊥平面PAB．(3)推导出CD⊥平面PAC.只需在棱PC上存在点F使得AF⊥PC即可．本题考查线面角的余弦值的求法，考查面面垂直的证明，考查线面垂直的判断与证明，考查空间点、线、面位置关系等基础知识，考查推理论证能力、运算求解能力，属于中档题．。

2020-2021学年吉林省长春实验中学高一（下）期末数学试卷一、单选题（本大题共12小题，共60.0分）1.已知i是虚数单位，则1+i1−i=()A. −1B. 1C. −iD. i2.若向量a⃗=(3,m)，b⃗ =(2,−1)，a⃗⊥b⃗ ，则实数m的值为()A. −32B. 32C. 2D. 63.某校1000名学生参加数学竞赛，随机抽取了20名学生的考试成绩(单位：分)，成绩的频率分布直方图如图所示，则下列说法正确的是()A. 频率分布直方图中a的值为0.004B. 估计这20名学生数学考试成绩的第60百分位数为80C. 估计这20名学生数学考试成绩的众数为80D. 估计总体中成绩落在[60,70)内的学生人数为1604.设α，β是空间两个不重合的平面，l，m是空间两条不重合的直线，下列命题不正确的是()A. 若l⊥α，l⊥β，则α//βB. 若l⊥α，m⊥α，则l//mC. 若l⊥α，l//β，则α⊥βD. 若l⊥α，α⊥β，则l//β5.为评估一种农作物的种植效果，选了n块地作试验田.这n块地的亩产量(单位：kg)分别为x1，x2，…，x n，下面给出的指标中可以用来评估这种农作物亩产量稳定程度的是()A. x1，x2，…，x n的平均数B. x1，x2，…，x n的标准差C. x1，x2，…，x n的最大值D. x1，x2，…，x n的中位数6. 如图，在直三棱柱ABC −A 1B 1C 1中，AC =BC =4，AC ⊥BC ，CC 1=5，D ，E 分别是AB ，B 1C 1的中点，则异面直线BE 与CD 所成的角的余弦值为( )A. √33B. 13C. √5829D. 3√87297. 随着高中新课程改革的不断深入，数学试题的命题形式正在发生着变化.某省示范性高中在数学试卷中加入了多项选择题.每道多项选择题给出的四个选项中，有多项符合题目要求.一同学解答一道多选题时，随机选了两个选项，若答案恰为两个选项，则该同学做对此题的概率为( )A. 16B. 111C. 14D. 1108. 唐狩猎纹高足银杯如图1，1963年出土于陕西省西安市沙坡村容藏，为唐代的酒具．它的盛酒部分可以近似地看作半球与圆柱的组合体(假设内壁表面光滑，忽略杯壁厚度)，如图2所示已知半球的半径为R ，酒杯内壁表面积为143πR 2，设酒杯上部分圆柱的体积为V 1，下部分半球的体积为V 2，则V1V 2=( )A. 2B. 32C. 1D. 349. 设锐角三角形ABC 的内角A ，B ，C 所对的边分别为a ，b ，c ，若a =2，B =2A ，则b 的取值范围为( )A. (0,4)B. (2,2√3)C. (2√2,2√3)D. (2√2,4)10. 已知△ABC 的三个内角A 、B 、C 所对的边分别为a 、b 、c ，满足cos 2A −cos 2B +cos 2C =1+sinAsinC ，且sinA +sinC =1，则△ABC 的形状为( )A. 等边三角形B. 等腰直角三角形C. 顶角为150°的等腰三角形D. 顶角为120°的等腰三角形11. 在如图所示的电路中，5只箱子表示保险匣，箱中所示数值表示通电时保险丝被切断的概率，若各保险匣之间互不影响，则当开关合上时，电路畅通的概率是( )A. 551720B. 29144C. 2972D. 293612. 如图，在棱长为1的正方体ABCD −A 1B 1C 1D 1中，P 为正方形ABCD 内(包括边界)的一动点，E ，F 分别为棱AB ，BC 的中点，若直线D 1P 与平面EFC 1无公共点，则线段D 1P 的长的范围是( )A. [√54,3√24] B. [3√24,√52] C. [3√24,3√54] D. [1,√52] 二、单空题（本大题共4小题，共20.0分）13. 在△ABC 中，点D 在直线AC 上，且AD ⃗⃗⃗⃗⃗⃗ =23AC ⃗⃗⃗⃗⃗ ，点E 在直线BD 上，且BD ⃗⃗⃗⃗⃗⃗ =2DE ⃗⃗⃗⃗⃗⃗ ，若AE ⃗⃗⃗⃗⃗ =λ1AB ⃗⃗⃗⃗⃗ +λ2AC⃗⃗⃗⃗⃗ ，则λ1+λ2=______． 14. 三棱锥P −ABC 中，PA ⊥平面ABC ，∠BAC =π2，AP =3，BC =6，则该三棱锥外接球的表面积为______．15. 如图，二面角α−l −β为60°，A ∈α，B ∈β，C ，D ，E ∈l ，∠BCD =45°，∠AED =30°，AE =2√2BC ，l ⊥平面ABD ，则直线AB 与平面β所成的角为______．16. 已知△ABC 三个内角A ，B ，C 的对应边分别为a ，b ，c ，且∠C =π3，c =2.则下列结论正确的序号是______． (1)△ABC 面积的最大值为√3；(2)AC ⃗⃗⃗⃗⃗ ⋅AB ⃗⃗⃗⃗⃗ 的最大值为2+4√33；(3)bcosA +acosB =√2； (4)cosBcosA的取值范围(−∞,√32)∪(√3,+∞)． 三、解答题（本大题共6小题，共70.0分）17. 已知向量a ⃗ 与b ⃗ 的夹角θ=2π3，且|a ⃗ |=3，|b ⃗ |=2．(1)求a ⃗ ⋅b ⃗ 及b ⃗ 在a ⃗ 上的投影向量； (2)求向量a ⃗ 与a ⃗ +b ⃗ 夹角的余弦值．18. 在平行六面体ABCD −A 1B 1C 1D 1中，AA 1=AB ，AB 1⊥B 1C 1．求证：(1)AB//平面A 1B 1C ； (2)平面ABB 1A 1⊥平面A 1BC ．19.从一批苹果中，随机抽取50个，其重量(单位：克)的频数分布表如下：分组(重量)[80,85)[85,90)[90,95)[95,100)频数(个)5102015(1)根据频数分布表计算苹果的重量在[90,95)的频率；(2)用分层抽样的方法从重量在[80,85)和[95,100)的苹果中共抽取4个，其中重量在[80,85)的有几个？(3)在(2)中抽出的4个苹果中，任取2个，求重量在[80,85)和[95,100)中各有1个的概率．20.如图，在△ABC中，点P在BC边上，∠PAC=60°，PC=2，AP+AC=4．(1)求边AC的长；(2)若△APB的面积是2√3，求sin∠BAP的值．21.随着社会的进步、科技的发展，人民对自己生活的环境要求越来越高，尤其是居住环境的环保和绿化受到每一位市民的关注.因此，2019年6月25日，生活垃圾分类制度入法，提倡每位居民做好垃圾分类储存、分类投放，方便工作人员分类搬运，提高垃圾的资源价值和经济价值，力争物尽其用.市环卫局在A、B两个小区分别随机抽取6户，进行生活垃圾分类调研工作，依据住户情况对近期一周(7天)进行生活垃圾分类占用时间统计如表：(1)分别计算A、B小区每周进行生活垃圾分类所用时间的平均值和方差；(2)如果两个小区住户均按照1000户计算，小区的垃圾也要按照垃圾分类搬运，市环卫局与两个小区物业及住户协商，初步实施下列方案：①A小区方案：号召住户生活垃圾分类“从我做起”，为了利国利民，每200位住户至少需要一名工作人员进行检查和纠错生活垃圾分类，每位工作人员月工资按照3000元(按照28天计算标准)计算，则每位住户每月至少需要承担的生活垃圾分类费是多少？②B小区方案：为了方便住户，住户只需要将垃圾堆放在垃圾点，物业让专职人员进行生活垃圾分类，一位专职工作人员对生活垃圾分类的效率相当于4位普通居民对生活垃圾分类效率，每位专职工作人员(每天工作8小时)月工资按照4000元(按照28天计算标准)计算，则每位住户每月至少需要承担的生活垃圾分类费是多少？③市环卫局与两个小区物业及住户协商分别试行一个月，根据实施情况，试分析哪个方案惠民力度大，值得进行推广？22.如图，已知三棱柱ABC−A1B1C1，平面A1ACC1⊥平面ABC，∠ABC=90°，∠BAC=30°，A1A=A1C=AC，E，F分别是AC，A1B1的中点．(Ⅰ)证明：EF⊥BC；(Ⅱ)求直线EF与平面A1BC所成角的余弦值．(Ⅲ)求二面角A−A1C−B的正弦值．答案和解析1.【答案】D【解析】解：∵1+i1−i =(1+i)2(1−i)(1+i)=2i2=i，故选：D．利用两个复数相除，分子和分母同时乘以分母的共轭复数，计算求得结果．本题主要考查两个复数代数形式的乘除法，虚数单位i的幂运算性质，属于基础题．2.【答案】D【解析】解：∵a⃗⊥b⃗ ，∴a⃗⋅b⃗ =6−m=0，解得m=6．故选：D．利用a⃗⊥b⃗ ⇔a⃗⋅b⃗ =0即可得出．本题考查了向量垂直于数量积的关系，属于基础题．3.【答案】B【解析】解：对于A，由频率分布直方图的性质得：(2a+3a+7a+6a+2a)×10=1，解得a=0.005，故A错误；对于B，[50,80)的频率为：10(2a+30+7a)=10×12×0.005=0.6，∴估计这20名学生数学考试成绩的第60百分位数为80，故B正确；对于C，估计这20名学生数学考试成绩的众数为：70+802=75，故C错误；对于D，估计总体中成绩落在[60,70)内的学生人数为：3×0.005×10×1000=150，故D错误．故选：B．对于A，由频率分布直方图的性质列方程能求出a；对于B，求出[50,80)的频率为0.6，由此能估计这20名学生数学考试成绩的第60百分位数为80；对于C，[70,80)对应的小矩形最高，由此能估计这20名学生数学考试成绩的众数；对于D，求出总体在[60,70)的频率，由此能估计总体中成绩落在[60,70)内的学生人数．本题考查命题真假的判断，频率分布直方图的性质等基础知识，考查运算求解能力、数据处理能力，是基础题．4.【答案】D【解析】解：对于A，由面面平行的判定定理得A正确；对于B，由直线与平面垂直的性质定理得B正确；对于C，l⊥α，l//β，则在β中一定β存在直线与l平行，由面面垂直的判定可得α⊥β，故C正确；对于D，若l⊥α，α⊥β，则l//β或l⊂β，故D正确；故选：D．A，由面面平行的判定定理判定；B，由直线与平面垂直的性质定理判定；C，由面面垂直的判定可判定；D，若l⊥α，α⊥β，则l//β或l⊂β；本题考查命题真假的判断，是中档题，解题时要认真审题，注意空间中线线、线面、面面间相互关系的合理运用．5.【答案】B【解析】【分析】本题考查可以用来评估这种农作物亩产量稳定程度的量的判断，解题时要认真审题，注意平均数、标准差、最大值、中位数的定义和意义的合理运用，属于基础题．利用平均数、标准差、最大值、中位数的定义和意义直接求解．【解答】解：在A中，平均数是表示一组数据集中趋势的量数，它是反映数据集中趋势的一项指标，故A不可以用来评估这种农作物亩产量稳定程度；在B中，标准差能反映一个数据集的离散程度，故B可以用来评估这种农作物亩产量稳定程度；在C中，最大值是一组数据最大的量，故C不可以用来评估这种农作物亩产量稳定程度；在D中，中位数将数据分成前半部分和后半部分，用来代表一组数据的“中等水平”，故D不可以用来评估这种农作物亩产量稳定程度．故选B．6.【答案】C【解析】【分析】本题考查空间几何体中异面直线所成角的余弦值，属于基础题．通过平行，找出异面直线所成角，运用余弦定理求解即可．【解答】解：取A1B1的中点D1，连接C1D1，因为D是AB的中点，则在直三棱柱ABC−A1B1C1中，C1D1//CD，取B1D1的中点F，连接EF、BF，因为E是B1C1的中点，所以C1D1//EF，所以EF//CD，所以∠FEB异面直线BE与CD所成的角(或其补角)，因为AC=BC=4，AC⊥BC，所以AB=4√2，B1E=2，而D是AB的中点，所以C1D1=CD=B1D1=2√2，所以B1F=EF=√2，因为在直三棱柱ABC−A1B1C1中，B1B=CC1=5，B1B⊥B1C1，B1B⊥A1B1，所以BF=√27，BE=√29，所以在三角形FEB中，cos∠FEB=EF2+BE2−BF22×EF×BE =√5829，所以异面直线BE与CD所成的角的余弦值为√5829．故选：C．7.【答案】A【解析】解：每道多项选择题给出的四个选项中，有多项符合题目要求．一同学解答一道多选题时，随机选了两个选项，基本事件总数n=C42=6，答案恰为两个选项，则该同学做对此题的概率为：P=C22C42=16．故选：A．基本事件总数n=C42=6，答案恰为两个选项，由此能求出该同学做对此题的概率．本题考查概率的求法，考查古典概型、排列组合等基础知识，考查运算求解能力等数学核心素养，是基础题．8.【答案】A【解析】解：设酒杯上部分(圆柱)的高为h，则酒杯内壁表面积为S=12×4πR2+2πRℎ=143πR2，解得ℎ=43R，∴V1=πR2ℎ=43πR3，V2=12×43πR3，∴V1V2=2．故选：A．设圆柱的高为h，根据题意可求得ℎ=43R，再分别表示出V1，V2即可得解．本题考查圆柱，球的体积及表面积的计算，考查运算能力，属于基础题．9.【答案】C【解析】解：因为锐角△ABC ，且B =2A ， ∴{0<A <π20<B =2A <π20<C =π−3A <π2，解得A ∈(π6,π4)， 所以cosA ∈(√22,√32)，由正弦定理知，asinA =bsinB =bsin2A =b2sinAcosA ， ∴b =2acosA =4cosA ∈(2√2,2√3). 故选：C ．由锐角△ABC ，可得A ∈(π6,π4)，再结合正弦定理和二倍角公式，推出b =4cosA ，从而得解．本题考查解三角形，熟练掌握正弦定理、二倍角公式和余弦函数的图象与性质是解题的关键，考查逻辑推理能力和运算能力，属于基础题．10.【答案】D【解析】 【分析】本题主要考查了正弦定理和余弦定理的应用．在解三角形问题中一般借助正弦定理和余弦定理边化角，角化边达到解题的目的，属于中档题．利用正弦定理把题设等式中的角的正弦转化成边，求得a ，b 和c 关系式，代入余弦定理中求得cos B 的值，进而求得B ，由sin 2B =sin 2A +sin 2C +sinAsinC ，与sinA +sinC =1联立求得sin A 和sin C 的值，进而根据A ，C 的范围推断出A =C ，即可判断得解． 【解答】解：∵cos 2A −cos 2B +cos 2C =1+sinAsinC ，∴(1−sin 2A)−(1−sin 2B)+(1−sin 2C)=1+sinAsinC ，∴可得sin 2A +sin 2C −sin 2B =−sinAsinC ，∴根据正弦定理得a2+c2−b2=−ac，∴由余弦定理得cosB=a2+c2−b22ac =−ac2ac=−12，∵0°<B<180°，∴B=120°，∵sin2B=sin2A+sin2C+sinAsinC．∴变形得34=(sinA+sinC)2−sinAsinC，又∵sinA+sinC=1，得sinAsinC=14，∴上述两式联立得sinA=sinC=12，∵0°<A<60°，0°<C<60°，∴A=C=30°，∴△ABC是顶角为120°的等腰三角形．故选：D．11.【答案】D【解析】【分析】本题考查相互独立事件同时发生的概率，考查学生分析问题的能力，属于中档题．前两个盒子为串联线路，求出它们不畅通的概率，利用对立事件的概率求出前3个盒子畅通的概率，后2个盒子为并联线路，求出它们畅通的概率，前3个盒子和后2个盒子又是串联线路，利用相互独立事件同时发生的概率公式，即可求电路畅通的概率．【解答】解：前两个盒子为串联线路，畅通的概率为12×23=13，所以不畅通的概率为1−13=23，则前三个盒子畅通的概率为1−23×14=56，后两个盒子畅通的概率为1−15×16=2930，所以当开关合上时，电路畅通的概率是2930×56=2936，故选D．12.【答案】B【解析】解：如图，取AD 的中点为G ，取CD 的中点为H ，连接D 1G ，D 1H ，GH ，AC ，由三角形中位线的性质可得，EF//AC ，GH//AC ， 则GH//EF ，∵EF ⊂平面C 1EF ，GH ⊄平面C 1EF ，可得GH//平面C 1EF ，连接GF ，可得GF//D 1C 1且GF =D 1C 1，则四边形GFC 1D 1为平行四边形，可得GD 1//C 1F ， ∵C 1F ⊂平面C 1EF ，D 1G ⊄平面C 1EF ，∴D 1G//平面C 1EF ，又D 1G ∩GH =G ，D 1G ，GH ⊂平面D 1GH ，∴平面D 1GH//平面C 1EF ， ∵直线D 1P 与平面EFC 1无公共点，∴点P 在线段GH 上，当P 为GH 的中点时，D 1P 取得最小值为√D 1D 2+DP 2=√12+(√24)2=3√24．当P 与G 或H 重合时，D 1P 取最大值为√12+(12)2=√52．∴线段D 1P 的长的范围是[3√24,√52]．故选：B ．取AD 的中点为G ，取CD 的中点为H ，连接D 1G ，D 1H ，GH ，证明平面D 1GH//平面C 1EF ，结合直线D 1P 与平面EFC 1无公共点，可得点P 在线段GH 上，由此求得线段D 1P 的长的范围．本题考查空间两点的距离的求法，考查空间中直线与平面的位置关系，考查转化思想和运算能力，属于中档题．13.【答案】12【解析】解：由BD ⃗⃗⃗⃗⃗⃗ =2DE ⃗⃗⃗⃗⃗⃗ ，得BA ⃗⃗⃗⃗⃗ +AD ⃗⃗⃗⃗⃗⃗ =2DA ⃗⃗⃗⃗⃗ +2AE ⃗⃗⃗⃗⃗ ，故AE ⃗⃗⃗⃗⃗ =12(3AD ⃗⃗⃗⃗⃗⃗ −AB ⃗⃗⃗⃗⃗ )， 所以AE ⃗⃗⃗⃗⃗ =12×2AC ⃗⃗⃗⃗⃗ −12AB ⃗⃗⃗⃗⃗ =−12AB ⃗⃗⃗⃗⃗ +AC ⃗⃗⃗⃗⃗ ， 故λ1=−12，λ2=1，所以λ1+λ2=12． 故答案为：12．根据三角形法则可得BA ⃗⃗⃗⃗⃗ +AD ⃗⃗⃗⃗⃗⃗ =2DA ⃗⃗⃗⃗⃗ +2AE ⃗⃗⃗⃗⃗ ，从而AE ⃗⃗⃗⃗⃗ =12(3AD ⃗⃗⃗⃗⃗⃗ −AB ⃗⃗⃗⃗⃗ )，结合AD ⃗⃗⃗⃗⃗⃗ =23AC ⃗⃗⃗⃗⃗ 即可用AB ⃗⃗⃗⃗⃗ 与AC ⃗⃗⃗⃗⃗ 表示出AE ⃗⃗⃗⃗⃗ ，进一步即可得出λ1+λ2的值．本题考查平面向量的基本定理及其意义，考查学生的逻辑推理和运算求解的能力，属于基础题．14.【答案】45π【解析】解：如图，∵PA⊥平面ABC，∠BAC=π，∴AB、AC、AP两两互相2垂直，把三棱锥P−ABC变形为长方体，则长方体的外接球即三棱锥P−ABC的外接球，长方体的对角线长为√PA2+AB2+AC2=√PA2+BC2=√9+36=√45，∴三棱锥外接球的表面积为4π×(√45)2=45π．2故答案为：45π．由题意可知，AB、AC、AP两两互相垂直，把三棱锥P−ABC变形为长方体，则长方体的外接球即三棱锥P−ABC的外接球，求出长方体的对角线长，可得外接球的半径，代入球的表面积公式得答案．本题考查多面体外接球表面积的求法，训练了分割补形法，是中档题．15.【答案】90°【解析】解：因为l⊥平面ABD，又AD，BD⊂平面ABD，则l⊥BD，l⊥AD，故∠BDA即为二面角α−l−β的平面角，所以∠ADB=60°，因为l⊥平面ABD，l⊂β，则平面β⊥平面ABD，故AB在平面β上的射影为BD，所以∠ABD为直线AB与平面β所成的角，设BC=1，则AE=2√2BC=2√2，,AD=√2，又∠BCD=45°，∠AED=30°，所以BD=√22在△ABD中，AB=√AD2+BD2−2AD⋅BD⋅cos∠ADB=√2+12−2×√2×√22×cos60°=√62，则cos∠ABD =AB 2+BD 2−AD 22AB⋅BD=32+12−22×√62×√22=0，故∠ABD =90°，所以直线AB 与平面β所成的角为90°． 故答案为：90°．由二面角的平面角的定义得到∠BDA 即为二面角α−l −β的平面角，由线面角的定义可得∠ABD 为直线AB 与平面β所成的角，在△ABD 中，利用余弦定理求解即可． 本题考查了二面角的应用以及线面角的求解，在使用几何法求线面角时，可通过已知条件，在斜线上取一点作该平面的垂线，找出该斜线在平面内的射影，通过解三角形求得，属于中档题．16.【答案】(1)(2)【解析】解：对于(1)：由余弦定理可得22=a 2+b 2−2abcos π3=a 2+b 2−ab ≥2ab −ab =ab ，当且仅当a =b 时，等号成立，S △ABC =12absinC ≤12×4×sin π3=√3，最大值为√3，故(1)正确； 对于(2)：AC⃗⃗⃗⃗⃗ ⋅AB ⃗⃗⃗⃗⃗ =bccosA =2bcosA ， 在△ABC 中，b sin(2π3−A)=c sinC =2sin π3，b =4√33sin(2π3−A)，bcosA =4√34sin(2π3−A)cosA =4√34(√32cosA +12sinA)cosA =4√33(√32cos 2A +12sinAcosA)=√33[√3(1+cos2A)+sin2A]=2√33sin(2A +π3)+1，因为C =π3， 所以0<A <2π3，所以π3<2A +π3<5π3，所以A =π12时，sin(2A +π3)取得最大值1，即b cos A 的最大值为2√33+1，所以AC⃗⃗⃗⃗⃗ ⋅AB ⃗⃗⃗⃗⃗ 的最大值为2+4√33，故(2)正确；对于(3)：由余弦定理bcosA+acosB=b×b2+c2−a22bc +a×a2+c2−b22ac=c=2，故(3)错误；对于(4)：B=2π3−A，cosBcosA=cos(2π3−A)cosA=−12cosA+√32sinAcosA=−12+√32tanA，A∈(0,2π3)，A=π2时，此式无意义，A∈(0,π2)，tanA>0，cosBcosA>−12，A∈(π2,2π3)时，tanA<−√3，cosBcosA<−2，故(4)错误．故答案为：(1)(2)．由余弦定理结合基本不不等式求得ab的最大值，即可得出面积的最大值，进而可判断(1)是否正确；由正弦定理结合二倍角公式，两角和与差的正弦公式，正弦函数性质求得b cos A的最大值，从而可得数量积的最大值，即可判断(2)是否正确；利用余弦定理变形判断(3)是否正确；根据A，B关系，结合两角差的余弦公式，正切函数性质求解判断(4)是否正确．本题考查命题的真假，解题中结合三角函数的性质，向量的数量积，属于中档题．17.【答案】解：(1)a⃗⋅b⃗ =|a⃗|⋅|b⃗ |cos2π3=3×2×(−12)=−3，b⃗ 在a⃗上的投影向量为|b⃗ |⋅cos2π3⋅a⃗|a⃗ |=2×(−12)×a⃗3=−13a⃗．(2)a⃗⋅(a⃗+b⃗ )=a⃗2+a⃗⋅b⃗ =9−3=6，|a⃗+b⃗ |=√(a⃗+b⃗ )2=√a⃗2+2a⃗⋅b⃗ +b⃗ 2=√9−2×3+4=√7，设向量a⃗与a⃗+b⃗ 夹角为α，则cosα=a⃗ ⋅(a⃗ +b⃗)|a⃗ |⋅|a⃗ +b⃗|=3×√7=2√77．【解析】(1)先由平面向量数量积的定义求出a⃗⋅b⃗ 的值，再根据平面向量的几何意义，即可得解；(2)先求得a⃗⋅(a⃗+b⃗ )的值，再由|a⃗+b⃗ |=√(a⃗+b⃗ )2，求出|a⃗+b⃗ |的值，最后由cosα=a⃗ ⋅(a⃗ +b⃗)|a⃗ |⋅|a⃗ +b⃗|，得解．本题考查平面向量的混合运算与数量积的几何意义，熟练掌握平面向量的运算法则是解题的关键，考查逻辑推理能力和运算能力，属于基础题．18.【答案】证明：(1)平行六面体ABCD−A1B1C1D1中，AB//A1B1，又AB⊂平面A1B1C,A1B1⊄平面A1B1C；得AB//平面A1B1C；(2)在平行六面体ABCD−A1B1C1D1中，AA1=AB，得四边形ABB1A1是菱形，AB1⊥A1B.在平行六面体ABCD−A1B1C1D1中，AA1=AB，AB1⊥B1C1⇒AB1⊥BC．又A1B∩BC=C，A1B⊂平面A1BC，BC⊂平面A1BC得AB1⊥面A1BC，且AB1⊂平面ABB1A1∴平面ABB1A1⊥平面A1BC．【解析】本题考查了平行六面体的性质，及空间线面平行、面面垂直的判定，属于中档题．(1)由AB//A1B1⇒AB//平面A1B1C；(2)可得四边形ABB1A1是菱形，AB1⊥A1B，由AB1⊥B1C1⇒AB1⊥BC⇒AB1⊥面A1BC，⇒平面ABB1A1⊥平面A1BC．19.【答案】解：(1)苹果的重量在[90,95)的频率为2050=0.4．(2)重量在[80,85)的有4⋅55+15=1个．(3)设这4个苹果中，重量在[80,85)段的有1个，编号为1.重量在[95,100)段的有3个，编号分别为2、3、4，从中任取两个，可能的情况有：(1,2)(1,3)(1,4)(2,3)(2,4)(3,4)共6种．设任取2个，重量在[80,85)和[95,100)中各有1个的事件为A，则事件A包含有(1,2)(1,3)(1,4)共3种，所以P(A)=36=12．【解析】(1)用苹果的重量在[90,95)的频数除以样本容量，即为所求．(2)根据重量在[80,85)的频数所占的比例，求得重量在[80,85)的苹果的个数．(3)用列举法求出所有的基本事件的个数，再求出满足条件的事件的个数，即可得到所求事件的概率．本题考查古典概型问题，用列举法计算可以列举出基本事件和满足条件的事件，应用列举法来解题是这一部分的最主要思想．本题还考查分层抽样的定义和方法，利用了总体中各层的个体数之比等于样本中对应各层的样本数之比，属于基础题．20.【答案】解：(1)在△ABC中，点P在BC边上，∠PAC=60°，PC=2，AP+AC=4．则：设AC=x，利用余弦定理得：PC2=AP2+AC2−2AP⋅AC⋅cos∠PAC，则：4=x2+(4−x)2−2x(4−x)⋅12，整理得：3x2−12x+12=0，解得：x=2故：AC=2；(2)由于AC=2，AP+AC=4，所以：AP=2，所以△APC为等边三角形．由于：△APB的面积是2√3，则：12⋅AP⋅BP⋅sin∠BPA=2√3，解得：BP=4．在△APB中，利用余弦定理：AB2=BP2+AP2−2⋅BP⋅AP⋅cos∠BPA，解得：AB=2√7，在△APB中，利用正弦定理得：BPsin∠BAP =ABsin∠BPA，所以：4sin∠BAP =√7√32，解得：sin∠BAP=√217．【解析】(1)根据三角形的边角关系式，利用余弦定理求出结果．(2)利用三角形的面积公式和正弦定理求出结果．本题考查的知识要点：正弦定理和余弦定理及三角形面积公式，主要考查学生的运算能力和转化能力，属于基础题型．21.【答案】解：(1)x A−=16(220+180+210+220+200+230)=210(分钟)，x B−=16(200+190+240+230+220+210)=215(分钟)，s A2=16[(220−210)2+(180−210)2+(210−210)2+(220−210)2+(200−210)2+(230−210)2]=8003=8003，s B2=16[(200−215)2+(190−215)2+(240−215)2+(230−215)2+(220−215)2+(210−215)2]=8753=8753；(2)①按照A方案，A小区一月至少需要5名工作人员进行检查和纠错生活垃圾分类，其费用是5×3000=15000元，每位住户每月需要承担的生活垃圾分类费为150001000=15(元)，②由(1)知，B小区平均每位住户每周需要215分钟进行垃圾分类，一月需要215×4= 860(分钟)，B小区一月平均需要860×1000=860000分钟的时间用于生活垃圾分类，∵一位专职工人一天的工作时间按照8小时作为计算标准，每月按照28天作为计算标准，一位专职工作人员对生活垃圾分类效果相当于4名普通居民对生活垃圾分类的效果，∴B小区一月需要专职工作人员至少8600008×60×28×4≈16(名)，则每位住户每月需要承担的生活垃圾分类费为16×40001000=64(元)，③根据上述计算可知，按照每位住户每月需要承担的生活垃圾分类费来说，选择A方案惠民力度大，但需要住户平时做好生活垃圾分类事项；如果对于高档小区的居民来说，可以选择B方案，这只是方便个别高收入住户，综上，选择A方案推广，有利于国民热爱劳动及素质的提升．【解析】(1)根据已知数据，利用平均数和方差公式即可求解；(2)①由题意可得A小区至少需要5名工作人员，乘以每位的月工资，再除以1000即可求得每位用户需要承担的生活垃圾分类费；②先求出B小区一个月用于生活垃圾分类所用的平均时间，从而可得B小区一个月需要专职工作人员数，乘以每位的月工资，再除以1000即可求得每位用户需要承担的生活垃圾分类费；③根据①②中的条件和结论，分析可得结论．本题主要考查平均数、方差的求法，考查运算求解能力，属于中档题．22.【答案】(Ⅰ)证明：连接A 1E ，∵A 1A =A 1C ，E 是AC 的中点，∴A 1E ⊥AC ，又平面A 1ACC 1⊥平面ABC ，A 1E ⊂平面A 1ACC 1，平面A 1ACC 1∩平面ABC =AC ，∴A 1E ⊥平面ABC ，如图，以E 为原点，在平面ABC 中，过E 作AC 的垂线为x 轴，EC ，EA 1所在直线分别为y ，z 轴，建立空间直角坐标系，设AC =4，则A 1(0,0，2√3)， B(√3,1,0)，B 1(√3,3,2√3)，F(√32,32,2√3)，A(0,−2,0)，C(0,2，0)，EF ⃗⃗⃗⃗⃗ =(√32,32,2√3)，BC ⃗⃗⃗⃗⃗ =(−√3,1,0)，由EF ⃗⃗⃗⃗⃗ ⋅BC ⃗⃗⃗⃗⃗ =0，得EF ⊥BC ． (Ⅱ)解：设直线EF 与平面A 1BC 所成角为θ，由(Ⅰ)得BC ⃗⃗⃗⃗⃗ =(−√3,1,0)，A 1C ⃗⃗⃗⃗⃗⃗⃗ =(0,2，−2√3)，设平面A 1BC 的法向量n ⃗ =(x,y ，z)，则{BC ⃗⃗⃗⃗⃗ ⋅n ⃗ =−√3x +y =0A 1C ⃗⃗⃗⃗⃗⃗⃗ ⋅n ⃗ =y −√3z =0， 取x =1，得n ⃗ =(1,√3,1)，∴sinθ=|EF ⃗⃗⃗⃗⃗ ⋅n ⃗⃗ ||EF ⃗⃗⃗⃗⃗ |⋅|n ⃗⃗ |=45， ∴直线EF 与平面A 1BC 所成角的余弦值为√1−(45)2=35． (Ⅲ)解：由(Ⅰ)可知：平面AA 1C 的一个法向量是m ⃗⃗⃗ =(1,0，0)，由图可知该二面角为锐二面角，设该二面角的平面角为φ，∵cos <m ⃗⃗⃗ ,n ⃗ >=|m ⃗⃗⃗ ⋅n ⃗⃗ ||m ⃗⃗⃗ |⋅|n ⃗⃗ |=√55，∴cosφ=√55,sinφ=√1−cos 2φ=2√55．【解析】(Ⅰ)连接A 1E ，证明A 1E ⊥AC ，推出A 1E ⊥平面ABC ，以E 为原点，在平面ABC 中，过E 作AC 的垂线为x 轴，EC ，EA 1所在直线分别为y ，z 轴，建立空间直角坐标系，通过求解EF ⃗⃗⃗⃗⃗ ⋅BC ⃗⃗⃗⃗⃗ =0，推出EF ⊥BC ．(Ⅱ)求出平面A1BC的法向量n⃗，利用空间向量的数量积求解直线EF与平面A1BC所成角的余弦值即可．(Ⅲ)求出平面AA1C的一个法向量利用空间向量的数量积求解二面角的正弦函数值即可．本题考查直线与平面垂直，直线与直线的位置关系的应用，空间直线与平面我曾经以及二面角的平面角的求法，考查空间想象能力，转化思想以及计算能力，是中档题．。

长春市名校2019-2020学年高一下期末复习检测数学试题一、选择题：本题共12小题，在每小题给出的四个选项中，只有一项是符合题目要求的。

1． “αβ=”是“sin sin αβ=”成立的（） A ．充分非必要条件. B ．必要非充分条件. C ．充要条件. D ．既非充分又非必要条件.【答案】A 【解析】 【分析】依次分析充分性与必要性是否成立. 【详解】αβ=时sin sin αβ=，而sin sin αβ=时αβ=不一定成立，所以“αβ=”是“sin sin αβ=”成立的充分非必要条件，选A. 【点睛】本题考查充要关系判定，考查基本分析判断能力，属基础题2．在锐角ABC 中，若30,4,A BC AC ︒===B 的大小为（ ） A ．30° B ．45°C ．60°D ．75°【答案】B 【解析】 【分析】直接利用正弦定理计算得到答案. 【详解】根据正弦定理得到：4sin 30sin B=︒，故sin B ，ABC 是锐角三角形，故45B =︒. 故选：B . 【点睛】本题考查了正弦定理解三角形，意在考查学生的计算能力.3．在ABC ∆中，角A ，B ，C 所对的边分别为a ，b ，c ，若22cos a b c B =+，则C =（ ） A ．2πB ．3π C ．4π D ．6π 【答案】B由题意和余弦定理可得222a b c ab +-=，再由余弦定理可得cos C ，可得角C 的值． 【详解】在ABC ∆中，2cos 2c B a b =-，∴由余弦定理可得222222a c b c a b ac+-⨯=-，222a b c ab ∴+-=， 2221cos 22a b c C ab +-∴==，又(0,)C π∈，3C π∴=．故选：B ． 【点睛】本题考查利用余弦定理解三角形，考查了转化思想，属基础题．4．如图，飞机的航线和山顶在同一个铅垂平面内，已知飞机的高度为海拔m ，速度为km/h ，飞行员先看到山顶的俯角为，经过80s 后又看到山顶的俯角为，则山顶的海拔高度为（ ）A ．B ．C ．D ．【答案】C 【解析】分析：先求AB 的长，在 中，可求BC 的长，进而由于CD ⊥AD ，所以CD=BCsin ∠CBD ，故可得山顶的海拔高度．详解：如图，，，∴在 中，山顶的海拔高度故选C ．点睛：本题以实际问题为载体，考查正弦定理的运用，关键是理解俯角的概念，属于基础题． 5．若()cos sin f x x x =-在[],a a -是减函数，则a 的最大值是 A ．4π B ．2π C ．34π D ．π【答案】A 【解析】 【详解】分析：先确定三角函数单调减区间，再根据集合包含关系确定a 的最大值.详解：因为π()cos sin 2)4f x x x x =-=+，所以由π02ππ2π,(k Z)4k x k +≤+≤+∈得π3π2π2π,(k Z)44k x k -+≤≤+∈ 因此π3ππ3ππ[,][,],,044444a a a a a a a -⊂-∴-<-≥-≤∴<≤，从而a 的最大值为π4，选A. 点睛：函数sin()(0,0)y A x B A ωϕω=++>>的性质：(1)max min =+y A B y A B =-，. (2)周期2π.T ω=(3)由ππ()2x k k ωϕ+=+∈Z 求对称轴， (4)由ππ2π2π()22k x k k ωϕ-+≤+≤+∈Z 求增区间； 由π3π2π2π()22k x k k ωϕ+≤+≤+∈Z 求减区间. 6．已知一直线经过两点()1,2A ，(),3B a ，且倾斜角为45，则a 的值为（ ） A ．-6 B ．-4C ．2D ．6【答案】C 【解析】 【分析】一直线经过两点()1,2A ，(),3B a ，则直线的斜率为321k a -=-． 直线的倾斜角为45 ∴32tan 4511a -==-，即2a =． 故答案选C ． 【点睛】本题考查了直线的斜率，意在考查学生的计算能力.7．若直线310x y ++=与直线2(1)10x a y +++=互相平行，则a 的值为（ ） A ．4 B ．43-C ．5D ．53-【答案】C 【解析】 【分析】根据两条存在斜率的直线平行，斜率相等且在纵轴上的截距不相等这一性质，可以求出a 的值. 【详解】直线310x y ++=的斜率为13-，在纵轴的截距为13-，因此若直线310x y ++=与直线()2110x a y +++=互相平行，则一定有直线()2110x a y +++=的斜率为13-，在纵轴的截距不等于13-，于是有2113a -=-+且1113a -≠-+，解得5a =，故本题选C. 【点睛】本题考查了已知两直线平行求参数问题.其时本题也可以运用下列性质解题： 若直线1110A x B y C ++=与直线2220A x B y C ++=平行， 则有1221A B A B =且1221A C A C ≠.8．已知：平面内不再同一条直线上的四点O 、A 、B 、C 满足AB AC μ=，若1()3OA OB OC R λλ=+∈，则μ=（ ） A ．1 B ．2C ．1-D ．2-【答案】D 【解析】 【分析】根据向量的加法原理对已知表示式转化为所需向量的运算对照向量的系数求解. 【详解】()()11113333,OA OB OC OA AB AC OA AB AC OA λλλλ=+++⎛⎫=++=+ ⎪+⎝⎭所以113λ+=，103AB AC λ+= ， 解得2.3λ=且2.AB AC =-故选D. 【点睛】本题考查向量的线性运算，属于基础题.9．圆2240x y x +-=的圆心坐标和半径分别为（ ） A ．02（，），2 B ．20（，），2 C ．20-（，），4 D ．20（，），4 【答案】B 【解析】试题分析：222240(2)4x y x x y +-=⇒-+=，所以圆心坐标和半径分别为（2,0）和2，选B. 考点：圆标准方程10．经过两条直线280x y +-=和210x y -+=的交点，且垂直于直线10x y -+=的直线方程为( ) A ．10x y --= B ．10x y +-=C ．50x y --=D ．50x y +-=【答案】D 【解析】 【分析】首先求出两条直线的交点坐标，再根据垂直求出斜率，点斜式写方程即可. 【详解】 有题知：280210x y x y +-=⎧⎨-+=⎩，解得：32x y =⎧⎨=⎩，交点(3,2).直线10x y -+=的斜率为1，所求直线斜率为1-. 所求直线为：2(3)y x -=--，即50x y +-=. 故选：D 【点睛】本题主要考查如何求两条直线的交点坐标，同时考查了两条直线的位置关系，属于简单题.11．若sin cos 0sin cos 0αααα>⎧⎨+<⎩则α所在象限为（ ）【解析】 【分析】根据已知不等式可得sin 0α<，cos 0α<；根据各象限内三角函数的符号可确定角所处的象限. 【详解】 由sin cos 0sin cos 0αααα>⎧⎨+<⎩知：sin 0α<，cos 0α<α在第三象限故选：C 【点睛】本题考查三角函数在各象限内的符号，属于基础题. 12．要得到函数2sin 26y x π⎛⎫=+⎪⎝⎭的图象，只需将函数2cos2y x =的图象 A ．向左平移3π个单位长度 B ．向右平移3π个单位长度C ．向左平移6π个单位长度 D ．向右平移6π个单位长度 【答案】D 【解析】 【分析】先将2sin 26y x π⎛⎫=+ ⎪⎝⎭化为2cos 26π⎡⎤⎛⎫=-⎪⎢⎥⎝⎭⎣⎦y x ，根据函数图像的平移原则，即可得出结果. 【详解】因为2sin 22cos 22cos 2636y x x x πππ⎡⎤⎛⎫⎛⎫⎛⎫=+=-=- ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦， 所以只需将2cos2y x =的图象向右平移6π个单位. 【点睛】本题主要考查三角函数的平移，熟记函数平移原则即可，属于基础题型. 二、填空题：本题共4小题 13．已知tan 3α=，则sin -2cos sin cos αααα=+____．【答案】14由于tan 3cos sin ααα==，则sin 3cos αα=，然后将sin 3cos αα=代入sin 2cos sin cos αααα-+中，化简即可得结果. 【详解】tan 3cos sin ααα==， sin 3cos αα∴=，2cos 3cos 2cos cos 1cos 3cos cos 4cos 4sin sin αααααααααα--∴===++，故答案为14.【点睛】本题考查了同角三角函数的关系，属于基础题. 同角三角函数之间的关系包含平方关系与商的关系，平方关系是正弦与余弦值之间的转换，商的关系是正余弦与正切之间的转换. 14．已知22ππα-<<，若tan 1α=-，则α=______.【答案】4π- 【解析】 【分析】由条件利用正切函数的单调性直接求出α的值． 【详解】 解：函数tan y x =在,22ππ⎛⎫- ⎪⎝⎭上单调递增，且22ππα-<<，若tan 1α=-，则4πα=-，故答案为：4π-． 【点睛】本题主要考查正切函数的单调性，根据三角函数的值求角，属于基础题． 15．定义11222n nn a a a H n-+++=为数列{}n a 的均值,已知数列{}n b 的均值12n n H +=,记数列{}n b kn -的前n 项和是n S ,若5n S S ≤对于任意的正整数n 恒成立,则实数k 的取值范围是________． 【答案】712[,]35【解析】 【分析】因为1112222n n n b b b n -+++⋯+=⋅,2121()2212n nn b b b n --++⋯+=-⋅,从而求出2(1)n b n =+,可得数列{}n b kn -为等差数列,记数列{}n b kn -为{}n c ,从而将5n S S ≤对任意的*(N )n n ∈恒成立化为0c ≥,0c ≤,即可求得答案.1112222n n nn b b b H n-++++==,∴ 1112222n n n b b b n -++++=⋅,故2121()(22212)n n n b b n b n --⋅++=-≥+,∴112212()n n n n b n n -+=⋅--⋅1()2n n =+⋅,则2(1)n b n =+,对1b 也成立,∴2(1)n b n =+,则()22n b kn k n -=-+,∴数列{}n b kn -为等差数列,记数列{}n b kn -为{}n c .故5n S S ≤对任意的*N ()n n ∈恒成立,可化为:50c ≥,60c ≤；即5(2)206(2)20k k -+≥⎧⎨-+≤⎩,解得,71235k ≤≤,故答案为:712[,]35． 【点睛】本题考查了根据递推公式求数列通项公式和数列的单调性,掌握判断数列前n 项和最大值的方法是解题关键,考查了分析能力和计算能力,属于中档题.16．已知数列{}n a 的首项11a =，其前n 项和为n S ，且212n n S S n n p ++=++，若{}n a 单调递增，则p的取值范围是__________． 【答案】13,22⎛⎫ ⎪⎝⎭【解析】由212n n S S n n p ++=++可得：()()()211212n n S S n n p n -+=-+-+≥两式相减得：()1212n n a a n n ++=+≥()1213n n a a n n -∴+=-≥两式相减可得：()1123n n a a n +--=≥∴数列a ，a ，a ...是以2为公差的等差数列，数列a ，a ，a ...是以2为公差的等差数列将2n =代入()1212n n a a n n ++=+≥可得34a p =-4223a a p =+=+要使得*n N ∀∈，1n n a a +<恒成立 只需要1234a a a a <<<即可1143p p p ∴<+<-<+解得1322p << 则p 的取值范围是1322⎛⎫⎪⎝⎭，点睛：本题考查了数列的递推关系求通项，在含有n S 的条件中，利用1n n n a S S -=-来求通项，本题利用减法运算求出数列隔一项为等差数列，结合11a =和数列为增数列求出结果，本题需要利用条件递推，有一点难度．三、解答题：解答应写出文字说明、证明过程或演算步骤。

长春市重点名校2019-2020学年高一下学期期末经典数学试题一、选择题：本题共12小题，在每小题给出的四个选项中，只有一项是符合题目要求的。

1．若非零实数,a b 满足a b <，则下列不等式成立的是（ ） A ．1a b< B ．2b a a b+≥ C ．2211ab a b< D ．22a a b b +<+【答案】C 【解析】 【分析】对每一个不等式逐一分析判断得解. 【详解】A,1a a b b b--=不一定小于0，所以该选项不一定成立； B,如果a ＜0，b ＜0时， 2b aa b+≥不成立，所以该选项不一定成立；C, 2222110a bab a b a b --=<，所以2211ab a b<，所以该不等式成立； D, 22()()()()(1)a a b b a b a b a b a b a b +-=+-+-=-++-不一定小于0，所以该选项不一定成立. 故选：C 【点睛】本题主要考查不等式性质和比较法比较实数的大小，意在考查学生对这些知识的理解掌握水平和分析推理能力.2．设ABC ∆的内角,,A B C 所对边的长分别为,,a b c ，若2,3sin 5sin b c a A B +==,则角C =（ ）A ．3πB ．23π C ．34πD ．56π【答案】B 【解析】 【分析】 【详解】试题分析：3sin 5sin A B =，由正弦定理可得35a b =即53a b =； 因为2b c a +=，所以73c b =，所以22222222549151999cos 51022233b b b a bc C ab b +--+-====-⨯，而(0,)C π∈，所以23C π=，故选B.考点：1.正弦定理；2.余弦定理.3．若一个数列的前三项依次为6，18，54，则此数列的一个通项公式为（ ）A ．42n a n =-B ．24n a n =+C ．23nn a =⨯ D ．32nn a =⨯【答案】C 【解析】 【分析】061636=⨯=⨯，1183636=⨯=⨯，2549636=⨯=⨯，可以归纳出数列的通项公式．【详解】依题意，061636=⨯=⨯，1183636=⨯=⨯，2549636=⨯=⨯，所以此数列的一个通项公式为-16323n nn a =⨯=⨯，故选：C ． 【点睛】本题考查了数列的通项公式，主要考查归纳法得到数列的通项公式，属于基础题．4．如图是一个边长为3的正方形二维码，为了测算图中黑色部分的面积，在正方形区域内随机投掷1089个点，其中落入白色部分的有484个点，据此可估计黑色部分的面积为（ ）A ．4B ．5C ．8D ．9【答案】B 【解析】 【分析】由几何概型中的随机模拟试验可得：S 605S 1089=黑正，将正方形面积代入运算即可． 【详解】由题意在正方形区域内随机投掷1089个点， 其中落入白色部分的有484个点， 则其中落入黑色部分的有605个点，由随机模拟试验可得：S 605S 1089=黑正，又9S 正=， 可得605951089S =⨯≈黑，故选B ． 【点睛】本题主要考查几何概型概率公式以及模拟实验的基本应用，属于简单题，求不规则图形的面积的主要方法就是利用 模拟实验，列出未知面积与已知面积之间的方程求解. 5．函数1tan 24y x π⎛⎫=+⎪⎝⎭的定义域是（ ）A ．{|2,}2x x k k Z ππ≠+∈ B ．{|4,}2x x k k Z ππ≠+∈C ．{|,}28k x x k Z ππ≠+∈ D ．{|,}8x x k k Z ππ≠+∈【答案】A 【解析】 【分析】利用复合函数求定义域的方法求出函数的定义域． 【详解】 令x+（k ∈Z ）， 解得：x（k ∈Z ），故函数的定义域为{x|x ，k ∈Z}故选A ． 【点睛】本题考查的知识要点：正切函数的性质的应用，主要考察学生的运算能力和转换能力，属于基础题型． 6．函数()cos f x x x x =+在[],ππ-上的图像大致为（ ）A ．B ．C ．D ．【答案】A 【解析】 【分析】利用函数的奇偶性和函数图像上的特殊点，对选项进行排除，由此得出正确选项. 【详解】由于()()()cos f x x x x f x -=-+=-，所以函数为奇函数，图像关于原点对称，排除C 选项.由于()π0f =，所以排除D 选项.由于ππππ03632f ⎛⎫=+=> ⎪⎝⎭，所以排除B 选项.故选：A. 【点睛】本小题主要考查函数图像的识别，考查函数的奇偶性、特殊点，属于基础题. 7．在等差数列中，若，，则（ ） A ．8 B ．16C ．20D ．28【答案】C 【解析】 【分析】 【详解】 因为为等差数列，则也成等差数列,公差为12-4=8所以,故选C.8．在平行四边形ABCD 中，若AB AD AB AD +=-，则必有（ ） A ．0AD = B ．0AB =或0AD = C ．ABCD 是矩形 D ．ABCD 是正方形【答案】C【解析】 【分析】由AB AD AB AD +=-，化简可得0AB AD ⋅=，得到AB AD ⊥,又由四边形ABCD 为平行四边形，即可得到答案. 【详解】由AB AD AB AD +=-，则22AB AD AB AD +=-， 即22()()AB AD AB AD +=-，化简可得0AB AD ⋅=， 所以AB AD ⊥，即AB AD ⊥,又由四边形ABCD 为平行四边形，所以该四边形ABCD 为矩形， 故选C. 【点睛】本题主要考查了向量的基本运算，以及向量的垂直关系的应用，其中解答中熟记向量的基本运算，以及向量的垂直的判定是解答的关键，着重考查了推理与运算能力，属于基础题.9．设数列{}n a 是公差不为零的等差数列，它的前n 项和为n S ，且1S 、2S 、4S 成等比数列，则31a a 等于（ ） A ．5 B ．4 C ．3 D ．2【答案】A 【解析】 【分析】设等差数列{}n a 的公差为()0d d ≠，根据2214S S S =得出1a 与d 的等量关系，即可计算出31a a 的值. 【详解】设等差数列{}n a 的公差为()0d d ≠，由于1S 、2S 、4S 成等比数列，则有2214S S S =，所以，()()2111246a d a a d +=+，化简得12d a =，因此，311111255a a d a a a a +===. 故选：A. 【点睛】本题考查等差数列前n 项和中基本量的计算，解题的关键就是结合题意得出首项与公差的等量关系，考查计算能力，属于基础题. 10．将函数()sin(2)3f x x π=-的图像左移3π个单位，则所得到的图象的解析式为A ．sin 2y x =B ．2sin(2)3y x π=+C ．sin(2)3y x π=+D ．2sin 23y x π=-（）【答案】C 【解析】 【分析】由三角函数的图象变换，将函数()f x 的图像左移3π个单位，得到sin[2()]33y x ππ=+-，即可得到函数的解析式. 【详解】由题意，将函数()sin(2)3f x x π=-的图像左移3π个单位，可得sin[2()]sin(2)333y x x πππ=+-=+的图象， 所以得到的函数的解析式为sin(2)3y x π=+，故选C.【点睛】本题主要考查了三角函数的图象变换，其中熟记三角函数的图象变换的规则是解答本题的关键，着重考查了分析问题和解答问题的能力，属于基础题. 11．若sin 0α<，且tan 0α>，则α是（ ） A ．第一象限角 B ．第二象限角C ．第三象限角D ．第四象限角【答案】C 【解析】sin 0α<，则α的终边在三、四象限；tan 0α>则α的终边在三、一象限， sin 0α<，tan 0α>，同时满足，则α的终边在三象限．12．已知各个顶点都在同一球面上的正方体的棱长为2，则这个球的表面积为（ ） A ．12π B ．16π C ．20π D ．24π【答案】A 【解析】 【分析】先求出外接球的半径，再求球的表面积得解. 【详解】由题得正方体的对角线长为23，所以223=2,3,=43=12R R S ππ∴=∴⋅球. 故选A 【点睛】本题主要考查多面体的外接球问题和球的表面积的计算，意在考查学生对这些知识的理解掌握水平和分析推理能力.二、填空题：本题共4小题13．如图所示为函数()sin()(0,0,0)f x A x A ωϕωϕ=+>>≤≤π的部分图像，其中M 、N 分别是函数图像的最高点和最低点，且||5MN =，那么(3)f -=________．【答案】1- 【解析】 【分析】由图可知：2A =，因为2226T AN MN AM==-=，由周期公式得到ω，结合(0)1f =以及诱导公式即可求解. 【详解】由图可知：2A =，因为2226T AN MN AM==-=所以263ππω== ，即()2sin 3f x x πϕ⎛⎫=+ ⎪⎝⎭由题意可知：(0)1f =，即1sin 2ϕ=1(3)2sin (3)2sin()2sin 2132f πϕπϕϕ⎛⎫-=⨯-+=-+=-=-⨯=- ⎪⎝⎭故答案为：1-【点睛】本题主要考查了正弦型函数的图像的性质以及求值，关键是从图像得出周期，最值等，属于基础题. 14．一船自西向东匀速航行,上午10时到达一座灯塔P 的南偏西75︒距塔64海里的M 处,下午2时到达这座灯塔的东南方向的N 处,则这只船的航行速度为__________海里/小时． 【答案】86【解析】由0000064sin 7564cos 7564245)642326MN =+=+==，行驶了4小时，这只船的航行速度为326864= 海里/小时． 【点睛】本题为解直角三角形应用题，利用直角三角形边角关系表示出两点间的距离，在用辅助角公式变形求值，最后利用速度公式求出结果.15．如图，在ABC 中，已知点D 在BC 边上，AD AC ⊥，3sin 333BAC AB AD ∠===，，，则BD 的长为____________．6 【解析】 【分析】由诱导公式可知cos BAD ∠，在ABD △中用余弦定理可得BD 的长。

2020-2021学年吉林省长春实验中学高一下学期期末考试数学试卷★祝考试顺利★(含答案)一、选择题（60分）1．已知i是虚数单位，则＝（）A．﹣1 B．1 C．﹣i D．i【分析】利用两个复数相除，分子和分母同时乘以分母的共轭复数，计算求得结果．解：∵＝＝＝i，故选：D．2．若向量＝（3，m），＝（2，﹣1），⊥，则实数m的值为（）A．﹣B．C．2 D．6【分析】利用⊥⇔＝0即可得出．解：∵⊥，∴＝6﹣m＝0，解得m＝6．故选：D．3．某校1000名学生参加数学竞赛，随机抽取了20名学生的考试成绩（单位：分），成绩的频率分布直方图如图所示，则下列说法正确的是（）A．频率分布直方图中a的值为0.004B．估计这20名学生数学考试成绩的第60百分位数为80C．估计这20名学生数学考试成绩的众数为80D．估计总体中成绩落在[60，70）内的学生人数为160【分析】对于A，由频率分布直方图的性质列方程能求出a；对于B，求出[50，80）的频率为0.6，由此能估计这20名学生数学考试成绩的第60百分位数为80；对于C，[70，80）对应的小矩形最高，由此能估计这20名学生数学考试成绩的众数；对于D，求出总体在[60，70）的频率，由此能估计总体中成绩落在[60，70）内的学生人数．解：对于A，由频率分布直方图的性质得：（2a+3a+7a+6a+2a）×10＝1，解得a＝0.005，故A错误；对于B，[50，80）的频率为：10（2a+30+7a）＝10×12×0.005＝0.6，∴估计这20名学生数学考试成绩的第60百分位数为80，故B正确；对于C，估计这20名学生数学考试成绩的众数为：＝75，故C错误；对于D，估计总体中成绩落在[60，70）内的学生人数为：3×0.005×10×1000＝150，故D错误．故选：B．4．设α，β是空间两个不重合的平面，l，m是空间两条不重合的直线，下列命题不正确的是（）A．若l⊥α，l⊥β，则α∥βB．若l⊥α，m⊥α，则l∥mC．若l⊥α，l∥β，则α⊥βD．若l⊥α，α⊥β，则l∥β【分析】A，由面面平行的判定定理判定；B，由直线与平面垂直的性质定理判定；C，由面面垂直的判定可判定；D，若l⊥α，α⊥β，则l∥β或l⊂β；解：对于A，由面面平行的判定定理得A正确；对于B，由直线与平面垂直的性质定理得B正确；对于C，l⊥α，l∥β，则在β中一定β存在直线与l平行，由面面垂直的判定可得α⊥β，故C正确；对于D，若l⊥α，α⊥β，则l∥β或l⊂β，故D正确；故选：D．。