精选题1_轴向拉压
- 格式:doc
- 大小:2.40 MB
- 文档页数:28

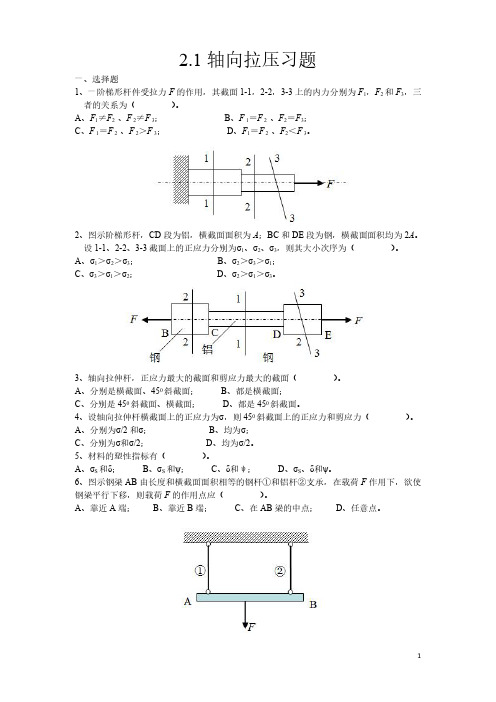
2.1轴向拉压习题一、选择题1、一阶梯形杆件受拉力F的作用,其截面1-1,2-2,3-3上的内力分别为F1,F2和F3,三者的关系为()。
A、F1≠F2、F2≠F3;B、F1=F2、F2=F3;C、F1=F2、F2>F3;D、F1=F2、F2<F3。
2、图示阶梯形杆,CD段为铝,横截面面积为A;BC和DE段为钢,横截面面积均为2A。
设1-1、2-2、3-3截面上的正应力分别为σ1、σ2、σ3,则其大小次序为()。
A、σ1>σ2>σ3;B、σ2>σ3>σ1;C、σ3>σ1>σ2;D、σ2>σ1>σ3。
3、轴向拉伸杆,正应力最大的截面和剪应力最大的截面()。
A、分别是横截面、450斜截面;B、都是横截面;C、分别是450斜截面、横截面;D、都是450斜截面。
4、设轴向拉伸杆横截面上的正应力为σ,则450斜截面上的正应力和剪应力()。
A、分别为σ/2和σ;B、均为σ;C、分别为σ和σ/2;D、均为σ/2。
5、材料的塑性指标有()。
A、σS和δ;B、σS和ψ;C、δ和ψ;D、σS、δ和ψ。
6、图示钢梁AB由长度和横截面面积相等的钢杆①和铝杆②支承,在载荷F作用下,欲使钢梁平行下移,则载荷F的作用点应()。
A、靠近A端;B、靠近B端;C、在AB梁的中点;D、任意点。
7、用三种不同材料制成尺寸相同的试件,在相同的试验条件下进行拉伸实验,得到应力-应变曲线图。
比较三条曲线,可知拉伸强度最高、弹性模量最大、塑性最好的材料分别是()。
A 、a 、b 、c ;B 、b 、c 、a ;C 、b 、a 、c ;D 、c 、b 、a 。
8、一拉伸钢杆,弹性模量E =200GPa ,比例极限为200MPa ,今测得其轴向应变ε=0.0015,则横截面上的正应力()。
A 、σ=Eε=300MPa ;B 、σ>300MPa ;C 、200MPa <σ<300MPa ;D 、σ<200MPa 。
9、变截面杆AD 受集中力作用,如图所示。

轴向拉伸与压缩练习题在材料力学中,轴向拉伸与压缩是一种常见的载荷方式,它们用于研究材料的强度、刚度和变形特性。
这些练习题旨在帮助学生加深对轴向拉伸与压缩的理解,并提供实践应用的机会。
以下是一些典型的练习题,通过解答这些问题,我们可以更好地理解这一领域的概念和原理。
1. 假设一根钢杆的长度为L,直径为D,已知拉伸载荷为F,求该杆的应力和应变。
2. 一根弹性体的长度为L,横截面积为A,已知施加在该体上的拉伸载荷为F,它的徐变模量为E,求该体的应变。
3. 如果一根杆材受到的拉伸载荷逐渐增加,最终达到其屈服强度,该杆材会发生什么样的变形?4. 如果一根杆材受到的压缩载荷逐渐增加,最终达到其屈服强度,该杆材会发生什么样的变形?5. 如果一根杆材同时受到轴向拉伸和压缩两种载荷,该杆材会如何变形?6. 一根弹性体的长度为L,横截面积为A,已知施加在该体上的拉伸载荷为F,计算该体的应力。
7. 一块材料在受到拉伸载荷时,其应力与应变之间的关系可以通过应力-应变曲线来表示,请描述应力-应变曲线的特点。
8. 如果一根杆材在受到轴向拉伸时断裂,这可能是由于哪些原因导致的?9. 一根杆材经过轴向拉伸后恢复原状的能力被称为什么?10. 在材料力学中,有一种称为胶黏剪切的变形模式,你了解它吗?请简要描述一下。
以上是一些典型的轴向拉伸与压缩练习题,通过解答这些问题,我们可以更好地理解轴向拉伸与压缩的基本概念和应用。
在解答问题的过程中,我们也可以运用公式和原理来计算并分析材料的应力、应变和变形等性质。
同时,通过这些练习题,我们可以培养应用知识解决实际问题的能力。
要提醒的是,在进行轴向拉伸与压缩练习题时,我们应该注意准确的计算和合理的分析。
在解答问题时,可以尝试用不同的方法和途径来验证答案,以加深对知识的理解和掌握。
同时,在实践中,我们也可以通过学习和研究更多的相关材料,来进一步拓展和深化对轴向拉伸与压缩的理解。
通过轴向拉伸与压缩练习题的学习与实践,我们可以更好地掌握这一领域的知识和技能。

1.衡。
设杆(A) qρ=(B)(C)(D)2.(A)(C)3. 在A和BA和点B(A) 0;(C) 45;。
4. 可在横梁(刚性杆)为A(A) [] 2A σ(C) []Aσ;5.(A)(C)6. 三杆结构如图所示。
今欲使杆3哪一种措施?(A) 加大杆3的横截面面积; (B) 减小杆3的横截面面积; (C) 三杆的横截面面积一起加大; (D) 增大α角。
7. 图示超静定结构中,梁AB 示杆1的伸长和杆2的缩短,(A) 12sin 2sin l l αβ∆=∆; (B) 12cos 2cos l l αβ∆=∆; (C) 12sin 2sin l l βα∆=∆; (D) 12cos 2cos l l βα∆=∆。
8. 图示结构,AC 为刚性杆,杆1(A) 两杆轴力均减小; (B) 两杆轴力均增大;(C) 杆1轴力减小,杆2轴力增大; (D) 杆1轴力增大,杆2轴力减小。
9. 结构由于温度变化,则:(A) (B) (C) (D) 10. 面n-n 上的内力N F 的四种答案中哪一种是正确的?(A) pD ; (B) 2pD;(C) 4pD ; (D) 8pD 。
11.的铅垂位移12. 截面的形状为13. 一长为l挂时由自重引起的最大应力14. 图示杆112A A >是N1F F 题1-141. D 2. D 3. C 4. B 5. B 6. B 7. C 8. C 9. B 10. B11. Fl EA ;12. ab;椭圆形 13. 22gl gl E ρρ, 14. >,= 15. 试证明受轴向拉伸的圆截面杆,其横截面沿圆周方向的线应变s ε等于直径的相对改变量d ε。
证:()s d πππd d ddddεε+∆-∆=== 证毕。
16. 如图所示,一实心圆杆1在其外表面紧套空心圆管2。
设杆的拉压刚度分别为11E A 和22E A 。
此组合杆承受轴向拉力F ,试求其长度的改变量。


轴向拉伸(压缩)的内力及强度计算一、判断题1.力是作用于杆件轴线上的外力。
()图 12.力越大,杆件越容易被拉断,因此轴力的大小可以用来判断杆件的强度。
()3.图1所示沿杆轴线作用着三个集中力,其m—m截面上的轴力为 N=-F。
()4.在轴力不变的情况下,改变拉杆的长度,则拉杆的绝对变化发生变化,而拉杆的纵向线应变不发生变化。
()5.轴力是指杆件沿轴线方向的内力。
()6.内力图的叠加法是指内力图上对应坐标的代数相加。
()7.轴力越大,杆件越容易被拉断,因此轴力的大小可以用来判断杆件的强度。
()8.两根等长的轴向拉杆,截面面积相同,截面形状和材料不同,在相同外力作用下它们相对应的截面上的内力不同()。
9.如图所示,杆件受力P作用,分别用N1、N2、N3和ζ1、ζ2、ζ3表示截面I-I、II-II、III-III上的轴力和正应力,则有(1)轴力N1> N2> N3()(2)正应力ζ1>ζ2>ζ 3 ()图 2 图 310.A、B两杆的材料、横截面面积和载荷p均相同,但L A> L B, 所以△L A>△L B (两杆均处于弹性范围内),因此有εA>εB。
()11.因E=ζ/ε,因而当ε一定时,E随ζ的增大而提高。
()12.已知碳钢的比例极限ζp=200MPa,弹性模量E=200Pa,现有一碳钢试件,测得其纵向线应变ε=0.002,则由虎克定律得其应力ζ=Eε=200×10×0.002=400Mpa。
()13.塑性材料的极限应力取强度极限,脆性材料的极限应力也取强度极限。
()14.现有低碳钢和铸铁两种材料,杆1选用铸铁,杆2选用低碳钢。
()图 415.一等直拉杆在两端承受拉力作用,若其一半段为钢,另一半段为铝,则两段的应力相同,变形相同。
()16.一圆截面轴向拉杆,若其直径增加一倍,则抗拉强度和刚度均是原来的2倍。
()17.铸铁的许用应力与杆件的受力状态(指拉伸或压缩)有关。
第三章 轴向拉伸和压缩一、选择题( )1、轴向拉伸或压缩时,直杆横截面上的内力称为轴力,表示为_______A.N FB. FSC.Q F D.jy F( )2、截面上的内力大小,________。
A.与截面的尺寸和形状无关B.与截面的尺寸有关,但与截面的形状无关C.与截面的尺寸无关,但与截面的形状有关D.与截面的尺寸和形状都有关( )3、等截面直杆在两个外力的作用下发生轴向压缩变形时,这对外力所具备的特点一 定是等值、_______。
A.反向、共线B.反向,过截面形心C.方向相对,作用线与杆轴线重合D.方向相对,沿同一直线作用( )4、一阶梯形杆件受拉力P的作用,其截面1-1,2-2,3-3上的内力分别为N1,N2 和N3,三者的关系为_______。
A.N1≠N2 N2≠N3B.N1=N2 N2=N3C.N1=N2 N2>N3D.N1=N2 N2<N3( )5、图示阶梯形杆,CD 段为铝,横截面面积为A ;BC 和DE 段为钢,横截面面积均为 2A 。
设1-1、2-2、3-3截面上的正应力分别为σ1、σ2、σ3,则其大小次序为_______。
A.σ1>σ2>σ3B.σ2>σ3>σ1C.σ3>σ1>σ2D.σ2>σ1>σ3( )6、轴向拉伸杆,正应力最大的截面和剪应力最大的截面_______。
A.分别是横截面、450斜截面B.都是横截面C.分别是450斜截面、横截面D.都是450斜截面( )7、由变形公式Δl =Pl/EA 即E =Pl/A Δl 可知,弹性模量_______。
A.与载荷、杆长、横截面面积无关B.与载荷成正比C.与杆长成正比D.与横截面面积成正比( )8、在下列说法,_______是正确的。
A 内力随外力增大而增大B 内力与外力无关C 内力随外力增大而减小D 内力沿杆轴是不变( )9、在轴向拉伸或压缩杆件上正应力为零的截面是_______。
A.横截面B.与轴线成一定交角的斜截面C.沿轴线的截面D.不存在的( )10、一圆杆受拉,在其弹性变形范围内,将直径增加一倍,则杆的相对变形将变为原 来的_______倍。
轴向拉压杆的内力自测题一、填空题1.2.3.4.二、选择题1. 轴向拉伸或压缩时,直杆横截面上的内力称为轴力,表示为()A F NB F SC F QD F Y2. 对于轴向拉压变形而言,其受力特点是指作用于杆件外力的合力作用线沿()方向。
A 垂直杆件轴线B 横截面切线C 45°斜截面D 杆件轴线3. 在下列说法()是正确的。
A 内力随外力增大而增大B 内力与外力无关C 内力随外力增大而减小D 内力沿杆轴是不变4. 关于轴力()。
A 是杆件轴线上的荷载B 是杆件截面上的内力C 与杆件的截面面积有关D 与杆件的材料有关5. 用截面法确定某截面的内力时,是对()建立平衡方程的。
A 该截面左段B 该截面右段C 该截面左段或右段D 整个杆6. 轴向拉、压杆,由截面法求得同一截面的左、右两部分的轴力,则两轴力大小相等,而()。
A 方向相同,符号相同。
B 方向相反,符号相同。
C 方向相同,符号相反。
D 方向相反,符号相反。
7. 杆件受力情况如图所示。
轴力为-5kN的截面是()A 4-4截面B 3-3截面C 2-2截面D 1-1截面8. 杆件受力情况如图所示, 若用max N F 和min N F 分别表示杆内的最大轴力和最小轴力,则下列结论中正确的是 ( )A max N F = 50kN ,min N F = -5kNB max N F = 55kN ,min N F = -40kNC max N F = 55kN ,min N F = -25kND max N F = 20kN ,min N F = -5kN三、 判断题1. 杆件的轴力仅与杆件所受外力有关,而与杆件的截面形状、材料无关。
( )2. 用截面法计算内力时,选取不同的研究对象,得到的内力正负号是不同的。
( )3. 轴力图在截面变化处会出现突变。
( )。
第二章轴向拉压一、选择题1.图1所示拉杆的外表面上有一斜线,当拉杆变形时,斜线将( D)A.平动B.转动C.不动D.平动加转动2.轴向拉伸细长杆件如图2所示,其中1-1面靠近集中力作用的左端面,则正确的说法应是( C)A.1-1、2-2面上应力皆均匀分布B.1-1、2-2面上应力皆非均匀分布C.1-1面上应力非均匀分布,2-2面上应力均匀分布D.1-1面上应力均匀分布,2-2面上应力非均匀分布(图1)(图2)3.有A、B、C三种材料,其拉伸应力—应变实验曲线如图3所示,曲线( B)材料的弹性模量E大,曲线( A )材料的强度高,曲线( C)材料的塑性好。
4.材料经过冷作硬化后,其( D)。
A.弹性模量提高,塑性降低B.弹性模量降低,塑性提高C.比例极限提高,塑性提高D.比例极限提高,塑性降低5.现有钢、铸铁两种杆材,其直径相同。
从承载能力与经济效益两个方面考虑,图4所示结构中两种合理选择方案是( A)。
A.1杆为钢,2杆为铸铁B.1杆为铸铁,2杆为钢C.2杆均为钢D.2杆均为铸铁(图3)(图4)(图5)6.在低碳钢的拉伸试验中,材料的应力变化不大而变形显著增加的是(B)。
A. 弹性阶段;B.屈服阶段;C.强化阶段;D.局部变形阶段。
7.铸铁试件压缩破坏(B)。
A. 断口与轴线垂直;B. 断口为与轴线大致呈450~550倾角的斜面;C. 断口呈螺旋面;D. 以上皆有可能。
8.为使材料有一定的强度储备,安全系数取值应( A )。
A .大于1; B. 等于1; C.小于1; D. 都有可能。
9. 等截面直杆在两个外力的作用下发生轴向压缩变形时,这对外力所具备的特点一定是等值、( C )。
A 反向、共线B 反向,过截面形心C 方向相对,作用线与杆轴线重合D 方向相对,沿同一直线作用10. 图6所示一阶梯形杆件受拉力P的作用,其截面1-1,2-2,3-3上的内力分别为N 1,N 2和N 3,三者的关系为( B )。
第一章轴向拉伸和压缩习题一、单项选择题1、构件具有足够的抵抗破坏的能力,我们就说构件具有足够的A、刚度,B、稳定性,C、硬度,D、强度。
2、构件具有足够的抵抗变形的能力,我们就说构件具有足够的A、强度,B、稳定性,C、刚度,D、硬度。
3、单位面积上的内力称之为A、正应力,B、应力,C、拉应力,D、压应力。
4、与截面垂直的应力称之为A、正应力,B、拉应力,C、压应力,D、切应力。
5、轴向拉伸和压缩时,杆件横截面上产生的应力为A、正应力,B、拉应力,C、压应力,D、切应力。
6、胡克定律在下述哪个范围内成立?A、屈服极限,B、比例极限,C、强度极限,D、名义屈服极限。
时,试样将7、当低碳钢试样横截面上的实验应力σ =σsA、完全失去承载能力,B、断裂,C、产生较大变形,D、局部出现颈缩。
8、脆性材料具有以下哪种力学性质?A、试样拉伸过程中出现屈服现象,B、抗冲击性能比塑性材料好,C、若构件开孔造成应力集中现象,对强度没有影响。
D、抗压强度极限比抗拉强度极限大得多。
9、灰铸铁压缩实验时,出现的裂纹A、沿着试样的横截面,B、沿着与试样轴线平行的纵截面,C、裂纹无规律,D、沿着与试样轴线成45。
角的斜截面。
10、横截面都为圆的两个杆,直径分别为d和D ,并且d=0.5D。
两杆横截面上轴力相等两杆横截面上应力之比Ddσσ为 A 、2倍, B 、4倍, C 、8倍, D 、16倍。
二、填空题1、求内力常用的方法是 。
2、轴向拉伸和压缩时,虎克定律的两种表达形式为 ,3、通过低碳钢拉伸试验可知,反映材料抵抗弹性变形能力的指标是 ;反映材料强度的指标是 ;反映材料塑性的指标是 。
4、σ0.2表示材料的 。
5、与截面平行的应力称为 ;与截面垂直的应力称之为 。
6、 钢的弹性模量E=200Gpa ,铝的弹性模量E=71Gpa,试比较在同一应力作用下,哪种材料应变大? 。
7、轴向拉伸和压缩时,杆上所受外力或外力的合力与杆件的轴线 。
轴向拉压(以切代弧)1. 等截面直杆CD位于两块夹板之间,如图示。
杆件与夹板间的摩擦力与杆件自重保持平衡。
设杆CD两侧的摩擦力沿轴线方向均匀分布,且两侧摩擦力的集度均为q,杆CD的横截面面积为A,质量密度为ρ,试问下列结论中哪一个是(A)(B)(C)(D)2.(A)(C)克3.[σ](A)(B)(C)(D)4.(A)(C)5.(A)(C) 外径减小,壁厚增大; (D) 外径增大,壁厚减小。
6. 三杆结构如图所示。
今欲使杆3的轴力减小,问应采取以下哪一种措施? (A) 加大杆3的横截面面积; (B) 减小杆3的横截面面积; (C) 三杆的横截面面积一起加大; (D) 增大α角。
7. 别表示杆1(A) α2sin 21l l ∆=∆(B) α2cos 21l l ∆=∆(C) β2sin 21l l ∆=∆(D) β2cos 21l l ∆=∆8. 图示结构,AC (A) (B) (C) 杆1(D) 杆19. (A) (B) (C) (D)10. 点A 的铅垂位移Ay Δ11.12. 一长为l ,横截面面积为A 的等截面直杆,质量密度为ρ,弹性模量为E ,该杆铅垂悬挂时由自重引起的最大应力=m ax σ ,杆的总伸长=∆l 。
积分13. 图示杆1和杆2的材料和长度都相同,但横截面面积1A >2A 。
若两杆温度都下降T ∆,则两杆轴力之间的关系是N1F N2F ,正应力之间的关系是1σ____2σ。
(填入符号<,=,>)题1-13答案:1. D2. D3. C4. B5. B6. B7. C8. C9. B10. EA Fl EA Fl 3; 11. ba;椭圆形 12. E gl gl 22ρρ, 13. >,= 14. 试证明受轴向拉伸的圆截面杆,其横截面沿圆周方向的线应变s ε等于直径的相对改变量d ε。
证:()d s πππεε=∆=-∆+=ddd d d d 证毕。
15. 如图所示,一实心圆杆1在其外表面紧套空心圆管2。
设杆的拉压刚度分别为11A E 和22A E 。
此组合杆承受轴向拉力F ,试求其长度的改变量。
(假设圆杆和圆管之间不发生相对滑动)解: 由平衡条件 F F F =+2N 1N (1变形协调条件222N 111N A E lF A E l F = (2) 由(1)(2)得 2211111N A E A E FlA E l F l +==∆ 16. 设有一实心钢管,在其外表面紧套一铜管。
材料的弹性模量和线膨胀系数分别为1E ,2E 和1l α,2l α,且2l α>1l α。
两管的横截面面积均为A 。
如果两者紧套的程度不会发生相互滑动,试证明当组合管升温T ∆后,其长度改变为()()212211E E T l E E l l l +∆+=∆αα。
证:由平衡条件 2N 1N F F = (1)钢)l∆17.q 解:18. AC圆拱σ[=]解F19. 应力[τ解:στα[][]21tan ==στα胶缝截面与横截面的夹角 57.26=α 20. 图示防水闸门用一排支杆支撑(图中只画出1根),各杆直径为mm 150=d 的圆木,许用应力[]MPa 10=σ,设闸门受的水压力与水深成正比,水的质量密度ρ=33m kg 100.1⨯,若不考虑支杆的稳定问题,试求支杆间的最大距离。
(取2s m 10=g )解:设支杆间的最大距离为x ,闸门底部A闸门AB 的受力如图∑=0A M ,αcos 413210F q =⨯⨯ N F F =≤[]2π41d σ53cos =α,m kN 3030x gx q ==ρ得:m 42.9=x21. 图示结构中AC 为刚性梁,BD 为斜撑杆,载荷F 可沿梁AC 水平移动。
试问:为使斜杆的重量最小,斜撑杆与梁之间的夹角θ应取何值?解:载荷F 移至C 处时,杆BD 的受力最大,如图。
θcos h FlF BD =A ≥[][]σθσcos h Fl F BD= 杆BD 的体积[]θσθ2sin 2sin Flh AV == 当12sin =θ时,V 最小即重量最轻,故4π=θ22. 图示结构,BC 为刚性梁,杆1和杆2力分别为[]1σ和[]2σ,且[][]212σσ=。
载荷F 移动,其移动范围为0≤x ≤l 。
试求:(1) 从强度方面考虑,当x 为何值时,许用载荷[F 最大,其最大值F 为多少?4(2) 该结构的许用载荷[]F 多大? 解:(1) 杆BC 受力如图1N F =[]A 1σ,2N F =[]A 2σ[][]A A F F F 12N21N max 233σσ==+=3l x =(2) F 在C 处时最不利 2N F F =≤[]A 2σ 所以结构的许用载荷 [][]A F 2σ=23. 图示结构,杆1和杆2的横截面面积为A ,材料的弹性模量为E ,其拉伸许用应力为[]+σ,压缩许用应力为[]-σ,且[][]+-=σσ2,载荷F 可以在刚性梁BCD(1) 结构的许用载荷[]F (2) 当x 为何值时(0<x 且最大许用值为多少?解:(1)F 在B ∑=0DM ,021N =⋅-l F l F1N 21F F =≤[]A-σ21∑=0CM,2N F F =≤[]A +σ结构的许用载荷 [][]A F +=σ(2) F 在CD 间能取得许用载荷最大值,梁受力如图(2)∑=0yF,02N 1N =-+F F F∑=0BM,022N 1N =-+Fx l F l Fx l l F F -=21N ,lx lF F -=2N F ≤[]xl Al --2σ,F ≤[]lx Al --σN2N2(1)N2(2)l x x l -=-121,23lx = [][]+-==σσA A F 42max24. 在图示结构中,杆BC 和杆BD 的材料相同,且受拉和受压时的许用应力相等,已知载荷F ,杆BC 长l ,许用应力[]σ。
为使结构的用料最省,试求夹角α的[][]σασαααcot cos sin cos 21lF Fl l A l A V +=+=),(00d d ααα==V0sin 1cos sin cos sin 020*******=--ααααα, 即0c o s s i n c o s 2s i n 02020202=-αααα 2tan 0=α当 74.540=α时,V 最小,结构用料最省。
25. 如图所示,外径为D ,壁厚为δ,长为l 的均质圆管,由弹性模量E ,泊松比ν的材料制成。
若在管端的环形横截面上有集度为q 的均布力作用,试求受力前后圆管的长度,厚度和外径的改变量。
解:长度的改变量 ElqE l l l ===∆σε厚度的改变量 Eqδννεδδεδ-=-='=∆外径的改变量 EqD D D D ννεε-=-='=∆26. 正方形截面拉杆,边长为cm 22,弹性模量GPa 200=E ,泊松比3.0=ν。
当杆受到轴向拉力作用后,横截面对角线缩短了mm 012.0,试求该杆的轴向拉力F 的大小。
解:对角线上的线应变3000.040012.0-=-='ε 则杆的纵向线应变001.0='-=νεε杆的拉力kN 160==EA F ε27. 图示圆锥形杆的长度为l ,材料的弹性模量为E ,质量密度为ρ,试求自重引起的杆的伸长量。
解:x 处的轴向内力 ()()()x x A g x gV x F ⋅==31N ρρ杆的伸长量()()()()⎰⎰⋅==∆l l x x EA x x gA x EA x x F l 0 0 Nd 3d ρ⎰==l Egl E x gx 0 263d ρρ28. 设图示直杆材料为低碳钢,弹性模量GPa 200=E ,杆的横截面面积为2cm 5=A ,杆长m 1=l ,加轴向拉力kN 150=F ,测得伸长mm 4=∆l 。
试求卸载后杆的残余变形。
解:卸载后随之消失的弹性变形mm 5.1e ==∆EAFll 残余变形为mm 5.2e p =∆-∆=∆l l l29. 图示等直杆,已知载荷F ,BC 段长l ,横截面面积A ,弹性模量E ,质量密度ρ,考虑自重影响。
试求截面B 的位移。
解:由整体平衡得gAl F C ρ34=BC 段轴力()⎪⎭⎫ ⎝⎛-=l x gA x F 34N ρ截面B 的位移())(65d 34d 2 0 0 N ↓-=⎪⎭⎫ ⎝⎛-==∆=⎰⎰Egl x EA l x gA EA xx F l Δl lBC B ρρ30. 已知图示结构中三杆的拉压刚度均为EA ,设杆AB 为刚体,载荷F ,杆AB 长l 。
试求点C 的铅垂位移和水平位移。
解:杆AB 受力如图0N2=F , 2N3N1F F F == l=1kNN3'xΔEAFll l Δy 231=∆=∆= 因为杆AB 作刚性平移,各点位移相同,且0N2=F ,杆2不变形。
又沿45由A 移至A '。
所以 EAFlΔΔy x 2== 31. 电子秤的传感器是一个空心圆筒,承受轴向拉伸或压缩。
已知圆筒外径mm 80=D ,壁厚mm 9=δ,材料的弹性模量GPa 210=E 。
在称某重物时,测得筒壁的轴向应变610476-⨯-=ε,试问该物重多少? 解:圆筒横截面上的正应力E AFεσ==()22π41d D E EA F -⋅==εεmm 622=-=δD d 该物重 kN 67.200=F32. 图示受力结构,AB 为刚性杆,CD 为钢制斜拉杆。
已知杆CD 的横截面面积2mm 100=A ,弹性模量GPa 200=E 。
载荷kN 51=F ,kN 102=F ,试求: (1)杆CD 的伸长量l ∆; (2)点B 的垂直位移B ∆。
解:杆AB 受力如图∑=0AM,022212N=--F F F ()kN 2202212N =+=F F F mm 2N ==∆EAlF l mm 66.5222=∆==l ΔΔC B33. 如图示,直径mm 16=d 的钢制圆杆ABBCD 在B 处铰接。
当D 处受水平力F 的纵向线应变9000.0=εGPa 210=E 。
试求: (1)力F 的大小; (2)点D 的水平位移。
11B解:折杆BCD 受力如图(1)∑=0C M ,025.1N =⨯-⨯F FkN 5.2825.125.1N===A E F F ε (2)mm 1.8m 8001.0===∆l l ε5.12lΔDx ∆= mm 4.25.12==l ΔDx ε34. 如图示等直杆AB 在水平面内绕A 端作匀速转动,角速度为ω,设杆件的横截面面积为A ,质量密度为ρ。
则截面C 处的轴力______________N =C F 。
答:⎪⎭⎫ ⎝⎛-22x l x A ωρ 从后往前0到X 积分35. 如图示,两端固定的等直杆AB ,已知沿轴向均匀分布的载荷集度为q ,杆长为l ,拉压刚度为EA ,试证明任意一截面的位移()EAx l qx x 2-=δ,最大的位移EA ql 82max =δ。