人教版八年级数学全等三角形的常见模型总结(精选.)

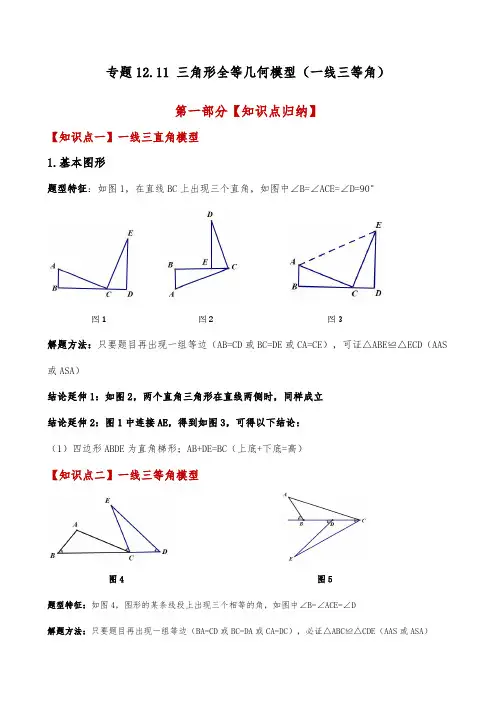
专题12.11三角形全等几何模型（一线三等角）第一部分【知识点归纳】【知识点一】一线三直角模型1.基本图形题型特征：如图1，在直线BC上出现三个直角，如图中∠B=∠ACE=∠D=90°图1图2图3解题方法：只要题目再出现一组等边（AB=CD或BC=DE或CA=CE），可证△ABE≌△ECD（AAS 或ASA）结论延伸1：如图2，两个直角三角形在直线两侧时，同样成立结论延伸2：图1中连接AE，得到如图3，可得以下结论：（1）四边形ABDE为直角梯形；AB+DE=BC（上底+下底=高）【知识点二】一线三等角模型图4图5题型特征：如图4，图形的某条线段上出现三个相等的角，如图中∠B=∠ACE=∠D解题方法：只要题目再出现一组等边（BA=CD或BC=DA或CA=DC），必证△ABC≌△CDE（AAS或ASA）结论延伸：如图5，两个三角形在直线两侧时，同样成立第二部分【题型展示与方法点拨】【题型1】直接用“一线三直角”模型求值或证明【例1】（23-24八年级上·安徽合肥·期末）如图，在ABC 中，90ACB ∠=︒，AC BC =，直线MN 经过点C ，且AD MN ⊥，BE MN ⊥，垂足分别为D E 、．（1）求证：ADC CEB ≌；（2）若3cm =AD ，5cm BE =，求四边形ABED 的面积．【变式1】（23-24八年级上·湖北武汉·阶段练习）如图，小虎用10块高度都是3cm 的相同长方体小木块，垒了两堵与地面垂直的木墙，木墙之间刚好可以放进一个等腰直角三角板（AC BC =，90ACB ∠=︒），点C 在DE 上，点A 和B 分别与木墙的顶端重合，则两堵木墙之间的距离DE 的长度为（）A ．30cmB ．27cmC ．21cmD ．10cm【变式2】（23-24九年级下·重庆开州·阶段练习）如图，在Rt ABC 中，90BAC ∠=︒，AB AC =，点D 为BC 上一点，连接AD ．过点B 作BE AD ⊥于点E ，过点C 作CF AD ⊥交AD 的延长线于点F ．若5BE =，2CF =，则EF 的长度为．【题型2】直接用“一线三等角”模型求值或证明【例2】（23-24八年级上·新疆昌吉·期中）已知ABC 是直角三角形，90BAC AB AC ∠=︒=，，直线l 经过点A ，分别过点B 、C 向直线l 作垂线，垂足分别为D 、E（1）如图a ，当点B 、C 位于直线l 的同侧时，证明：ABD CAE≌（2）如图b ，锐角ABC 中，AB AC =，直线l 经过点A ，点D 、E 分别在直线l 上，点B ，C 位于l 的同一侧，如果CEA ADB BAC ∠=∠=∠，请找到图中的全等三角形，并写出线段ED EC 、和DB 之间的数量关系【变式1】（21-22八年级上·浙江温州·期中）如图，在△ABC 中，AB ＝AC ＝9，点E 在边AC 上，AE 的中垂线交BC 于点D ，若∠ADE ＝∠B ，CD ＝3BD ，则CE 等于（）A ．3B ．2C ．94D ．92【变式2】（23-24七年级下·吉林长春·期中）如图，在ABC 中，AB AC =，AB BC >，点D 在边BC 上，且2CD BD =，点E 、F 在线段AD 上．CFD BED BAC ∠=∠=∠，ABC 的面积为18，则ABE 与CDF 的面积之和．【题型3】构造“一线三直角”模型求值或证明【例3】（23-24八年级上·山西吕梁·期末）数学课上，老师让同学们利用三角形纸片进行操作活动，探究有关线段之间的关系问题情境：如图1，三角形纸片ABC 中，90ACB ∠=︒，AC BC =.将点C 放在直线l 上，点A ，B 位于直线l 的同侧，过点A 作AD l ⊥于点D初步探究：（1）在图1的直线l 上取点E ，使BE BC =，得到图2，猜想线段CE 与AD 的数量关系，并说明理由；（2）小颖又拿了一张三角形纸片MPN 继续进行拼图操作，其中90MPN ∠=︒，MP NP =.小颖在图1的基础上，将三角形纸片MPN 的顶点P 放在直线l 上，点M 与点B 重合，过点N 作NH l ⊥于点H .如图3，探究线段CP ，AD ，NH 之间的数量关系，并说明理由【变式1】（23-24八年级上·新疆喀什·期中）如图，906AC AB BD ABD BC ==∠=︒=，，，则BCD △的面积为（）A ．9B ．6C ．10D ．12【变式2】（20-21七年级下·黑龙江哈尔滨·期末）如图，在ABC 中，90ABC ∠=︒，过点C 作CD AC ⊥，且CD AC =，连接BD ，若92BCD S = ，则BC 的长为．【题型4】“一线三直（等）角”模型的延伸与拓展【例4】如图，A 点的坐标为（0，3），B 点的坐标为（-3.0），D 为x 轴上的一个动点，AE ⊥AD ，且AE=AD ，连接BE 交y 轴于点M（1）若D点的坐标为（-5.0），求E点的坐标:（2）求证:M为BE的中点（3）当D点在x轴上运动时，探索:OMBD为定值【变式1】（23-24八年级上·陕西西安·阶段练习）勾股定理被誉为“几何明珠”．在我国古算书《周髀算经》中就有“若勾三，股四，则弦五”的记载．如图所示，把一个边长分别为3，4，5的三角形和三个正方形放置在大长方形ABCD中，则该长方形中空白部分的面积为（）A．54B．60C．100D．110【变式2】已知：四边形ABCD中，AB=AD=CD，∠BAD=90°，三角形ABC的面积为1，则线段AC的长度是.第三部分【中考链接与拓展延伸】1、直通中考【例1】（2021·四川南充·中考真题）如图，90BAC ∠=︒，AD 是BAC ∠内部一条射线，若AB AC =，BE AD ⊥于点E ，CF AD ⊥于点F ．求证：AF BE =．【例2】（2023·重庆·中考真题）如图，在Rt ABC △中，90BAC ∠= ，AB AC =，点D 为BC 上一点，连接AD ．过点B 作BE AD ⊥于点E ，过点C 作CF AD ⊥交AD 的延长线于点F ．若4BE =，1CF =，则EF 的长度为．2、拓展延伸【例1】（22-23八年级下·河南洛阳·期中）综合与实践数学活动课上，老师让同学们以“过等腰三角形顶点的直线”为主题开展数学探究．（1）操作发现：如图甲，在Rt ABC △中，90BAC ∠=︒，且AB AC =，直线l 经过点A ．小华分别过B 、C 两点作直线l 的垂线，垂足分别为点D 、E ．易证ABD CAE △△≌，此时，线段DE 、BD 、CE 的数量关系为：；（2）拓展应用：如图乙，ABC 为等腰直角三角形，90ACB ∠=︒，已知点C 的坐标为(2,0)-，点B 的坐标为(1,2)．请利用小华的发现直接写出点A 的坐标：；（3）迁移探究：①如图丙，小华又作了一个等腰ABC ，AB AC =，且90BAC ∠≠︒，她在直线l 上取两点D 、E ，使得BAC BDA AEC ∠=∠=∠，请你帮助小华判断（1）中线段DE 、BD 、CE 的数量关系是否变化，若不变，请证明；若变化，写出它们的关系式并说明理由；②如图丁，ABC 中，2AB AC =，90BAC ∠≠︒，点D 、E 在直线l 上，且BAC BDA AEC ∠=∠=∠，请直接写出线段DE 、BD 、CE 的数量关系．【例2】（22-23八年级上·广东惠州·期中）如图1，90ACB AC BC AD CE BE CE ∠==⊥⊥，，，，垂足分别为D ，E ．（1）若 2.5cm 1.7cm AD DE ==，，求BE 的长．（2）在其它条件不变的前提下，将CE 所在直线变换到ABC 的外部（如图2），请你猜想AD DE BE ，，三者之间的数量关系，并证明你的结论；（3）如图3，将（1）中的条件改为：在ABC 中，AC BC =，D ，C ，E 三点在同一条直线上，并且有BEC ADC BCA α∠=∠=∠=，其中α为任意钝角，那么（2）中你的猜想是否还成立？若成立，请证明；若不成立，请说明理由．。

人教版 八年级数学上册 第12章 全等三角形之垂直模型（含答案）1.三垂直模型（1）如图，已知矩形中，E 是AD 上的一点，F 是AB 上的一点，，且ABCD EF EC ⊥，，矩形的周长为32cm ，求AE 的长．EF EC =4DE cm =ABCD EF DCBA【答案】6cm ．（2）已知：如图，在ABC 中，，CD ⊥AB 于点D ，点E 在AC 上，V 90ACB ∠=︒CE =BC ，过E 点作AC 的垂线，交CD 的延长线于点F ．求证：AB =FC．【答案】易证，所以．Rt CEF Rt BCA ∆∆≌AB CF =（3）如图，在中，,，CF 交AB 于点E ，，Rt ABC △AC BC =90ACB ∠=︒BD CF ⊥，若，，求CF 的长.AF CF ⊥5DF =3AF =【答案】易证：，∴，．Rt ACF Rt BCD ∆∆≌3CD AF ==8CF CD DF =+=2.在中，，，直线经过点，且于，ABC △90ACB ∠=︒AC BC =MN C AD MN ⊥D 于．BE MN ⊥E （1）当绕点旋转到图1的位置时，请你探究线段、、之间的数量关系；MN C DE AD BE （2）当绕点旋转到图2的位置时，你在（1）中得到的结论是否发生变化？请写出MN C 你的猜想，并加以证明；（3）当绕点旋转到图3的位置时，你在（1）中得到的结论是否发生变化？请写出MN C 你的猜想，并加以证明．图1NMABCDE图2MNABCDE图3NMAC D E 【答案】（1）三垂直模型，易得，所以有；ACD CBE ≅△△DE AD BE =+（2）猜想：（1）中得到的结论发生了变化，同理可证：．DE AD BE =-（3）猜想：（1）中得到的结论发生了变化，同理可证：．DE BE AD =-3.已知等腰中，为直角，为的中点，于点G ．求证：Rt ABC △C ∠M BC CD AM ⊥．∠=∠AMC DMBB EB BC【答案】如图，过作，交延长线于．⊥CD E三垂直模型，易证：，≌∆∆Rt CBE Rt ACMM BC=∵为的中点，∴，．∠=∠=AMC ECM BM BE∠=∠∵，而，∴．∠=︒EBD MBDMBD∠+∠=︒4590MBD EBD≌E DMB AMC∆∆BD BED BMD又为公共边，∴，∴．∠=∠=∠4.已知CD是经过∠BCA顶点C的一条直线，CA=CB，E、F分别是直线CD上两点，且．∠=∠=∠BEC CFAα（1）如图1，若∠BCA=60°，时，线段BE和CF大小关系如何，猜想线段α∠=︒120BE、AF、和EF之间的数量关系，并证明．（2）如图2，若时，（1）中的结论是否仍然成立，请说明．∠=︒-180BCAα【答案】（1），；（2）成立．BE CF =EF BE AF =-5.（1）如图1，在中，，D 、A 、E 三点都在直线m 上，并且有ABC △AB AC =，其中α为任意锐角或钝角，请证明DE 、BD 、CE 三条线段的BDA AEC BAC α∠=∠=∠=数量关系．（2）在（1）的基础上，D 、E 是直线m 上两个动点（D 、A 、E 三点不重合），点F 是的平分线上一点，且、均为等边三角形，连接DF 、EF ，判断BAC ∠ABF △ACF △的形状，并证明．DEF △图1图2【答案】（1）∵，，易证,BDA AEC BAC α∠=∠=∠=AB AC =ADB CEA ≅△△∴，． BD AE AD CE ==，DE BD CE =+（2）是等边三角形．由（1）知：DEF △，∴，ADB CEA ≅△△ BD EA DBA CAE =∠=∠， 又∵、均为等边三角形，∴，ABF △ACF △60ABF CAF ∠=∠=︒，FBD FAE ∠=∠∴,，，∴，等边．DBF EAF ≅△△DF EF =BFD AFE ∠=∠60DFE ∠=︒DEF △6.如图，在中，是斜边上的高，是的平分线，交 于Rt ABC ∆AD BC BE ABC ∠AD BE ，于，求证：．O EF AD ⊥F AF OD =【答案】如图，过作．O OG AB ⊥∵，，∴．12∠=∠OD BC ⊥OG OD =∵，，∴．190AEO ∠+∠=︒290BOD ∠+∠=︒AEO BOD ∠=∠而，∴，∴．BOD AOE ∠=∠AEO AOE ∠=∠AE AO =∵，∴．EF DC ∥AEF C ∠=∠∵，，90C CAD ∠+∠=︒90GAO CAD ∠+∠=︒∴，故．C GAO ∠=∠AEF GAO ∠=∠∴，，∴．Rt AEF Rt OAG ∆∆≌OG AF =AF OD =（也可以过E 作BC 的垂线，按照模型来证明．）7.如图1，在中，，，垂足为D ．AF 平分，交Rt ABC △90ACB ∠=︒CD AB ⊥CAB ∠CD 于点E ，交CB 于点F ．图1 图2（1）求证：．CE CF =（2）将图1中的沿AB 向右平移到的位置，使点落在BC 边上，其它ADE △'''A D E △'E 条件不变，如图2所示．试猜想：与CF 有怎样的数量关系?请证明你的结论．'BE 【答案】（1）在中，；在中，Rt AED △90EAD AED ∠+∠=︒Rt ACF △；90CAF AFC ∠+∠=︒又有，∴，则有．CAF EAD ∠=∠AFC AED CEF ∠=∠=∠CE CF =（2）如图，过点E 作于G ，易证：，∴，EG AC ⊥''CEG BE D ≅△△'CE BE =由（1）中的结论，可得：．'CF BE =E‘图2G A ′FE CBA8.如图1，已知ABC 是等边三角形，点D 是边BC 的中点，∠ADE =60°，且DE 与V ∠ACB 的外角平分线CE 相交于点E ．过点作交于点，则有D DF AC ∥AB F ，易证：ADE 是等边三角形．那么请问：ADF EDC ≅△△V （1）若D 是线段BC 上(B 、C 点除外)的任意一点，其他条件不变（如图2），试判断ADE 的形状，并说明理由．V （2）若D 是BC 的延长线上（C 点除外）的任意一点，其他条件不变（如图3），那么（1）的结论是否仍然成立？请说明理由．图1 图2 图3【答案】（1）等边三角形；（2）成立，过点作交的延长线于点，则有，即证．D DF AC∥AB F AFD DCE≌∆∆9.如图，在ABC中，∠ACB=90°，AC=BC，直线MN经过点C，且AD⊥MN于点VD，BE⊥MN于点E，AD=5，BE=2，求线段DE的长．【答案】;710.如图，已知中，AC=BC，D是BC的中点，，垂足为Rt ABCV90ACB∠=o CE AD⊥E．，交CE的延长线于点F．求证：AC=2BF．BF ACPABC DEF 【答案】∵，，∴，．90ACB ∠=oBF AC P 90ACD CBF ∠=∠=o90ADC CAD ∠+∠=o∵，∴，∴．CE AD ⊥90FCB ADC ∠+∠=oCAD FCB ∠=∠又∵AC =CB ，∴，∴DC =FB ．ADC CFB ≅V V ∵D 是BC 的中点，∴BC =2BF ，即AC =2BF ．11.如图，中，，，D 是AB 上任意一点， 交CDABC △AC BC =90ACB ∠=︒AE CD ⊥延长线于E ，于F ．求证：．BF CD ⊥EF BF AE =-F E D CBA【答案】三垂直模型，易证：，则CE =BF ，AE =CF ，∴EF =CE -CF =BF -AE ．ACE CBF ≅V V 12.（1）如图，在中，，点、、分别在边、、上，且ABC △AB AC =D E F AB BC AC ，．图中是否存在和全等的三角形？说明理由．BD CE =DEF B ∠=∠BDE △FEDCBA(2)如图，在等边ABC 的边BC 上任取一点D ，作∠ADE =60°，DE 交∠C 的外角平分线于V E ，则ADE 是____________三角形．V 【答案】（1）；（2）等边．CEF 13.如图，已知△ABC 中，∠ACB =90°，CD ⊥AB 于D ，∠ABC 的角平分线BE 交CD 于G ，交AC 于E ，M 是CG 上一点且满足CM =DG . 求证：EM //AB .【答案】提示：过点作的垂线．G BC 14.八年级数学兴趣小组展示了他们小组探究的过程和发现的结果，内容如下：(1)如图1，正三角形ABC 中，在AB 、AC 边上分别取点M 、N ，使BM =AN ，连接BN 、CM ，发现BN =CM ，当M 、N 改变位置且保持BM =AN 时，∠NOC 保持不变，请猜测∠NOC 的度数：∠NOC =______度．(2)如图2，正方形ABCD 中，在AB 、BC 边上分别取点M 、N ，使AM =BN ，连接AN 、DM ，那么AN =DM ，且∠DON =_______度．(3)如图3，正五边形ABCDE 中，在AB 、BC 边上分别取点M 、N ，使AM =BN ，连接AN 、EM ，那么AN =EM ，且∠EON =________度．(4)在正n 边形中，对相邻的三边实施同样的操作过程，也会有类似的结论．请大胆猜测，用一句话概括你的发现：______________________________________.【答案】(1); (2) ；(3)；(4)以上所求的角正好等于正边形的内角60︒90︒108︒n ()2180n n-︒。

八年级数学上册第十二章全等三角形知识点总结归纳单选题1、如图，OD平分∠AOB，DE⊥AO于点E，DE=5，点F是射线OB上的任意一点，则DF的长度不可能是（）A．4B．5C．6D．7答案：A分析：根据角平分线的性质，可知点D到OB和OA的距离相等，并且点到直线的线段中，垂线段最短，最短距离为5，即可判断．∵OD平分∠AOB，DE⊥AO于点E，DE=5，∴D到OB的距离等于5，∴DF≥5故DF的长度不可能为4，故选A．小提示：本题考查了角平分线的性质，点到直线的线段中，垂线段最短，熟练掌握性质是本题的关键．2、下列说法正确的是（）A．两个面积相等的图形一定是全等图形B．两个全等图形形状一定相同C．两个周长相等的图形一定是全等图形D．两个正三角形一定是全等图形答案：B分析：根据全等图形的定义进行判断即可．解：A：两个面积相等的图形不一定是全等图形，故A错误，不符合题意；B：两个全等图形形状一定相同，故B正确，符合题意；C：两个周长相等的图形不一定是全等图形，故C错误，不符合题意；D：两个正三角形不一定是全等图形，故D错误，不符合题意；故选：B．小提示：本题考查了全等图形，熟练运用“能够完全重合的两个图形叫做全等形”是本题的关键．3、如图，在△ABC中，AD是BC边上的高，∠BAF=∠CAG=90°，AB=AF，AC=AG，连接FG，交DA的延长线于点E，连接BG，CF，则下列结论：①BG=CF；②BG⊥CF；③∠EAF=∠ABC；④EF=EG，其中正确的有（）A．①②③B．①②④C．①③④D．①②③④答案：D分析：证得△CAF≌△GAB（SAS），从而推得①正确；利用△CAF≌△GAB及三角形内角和与对顶角，可判断②正确；证明△AFM≌△BAD（AAS），得出FM=AD，∠FAM=∠ABD，则③正确，同理△ANG≌△CDA，得出NG=AD，则FM=NG，证明△FME≌△GNE（AAS）．可得出结论④正确．解：∵∠BAF=∠CAG=90°，∴∠BAF+∠BAC=∠CAG+∠BAC，即∠CAF=∠GAB，又∵AB=AF=AC=AG，∴△CAF≌△GAB（SAS），∴BG=CF，故①正确；∵△FAC≌△BAG，∴∠FCA=∠BGA，又∵BC与AG所交的对顶角相等，∴BG与FC所交角等于∠GAC，即等于90°，∴BG⊥CF，故②正确；过点F作FM⊥AE于点M，过点G作GN⊥AE交AE的延长线于点N，∵∠FMA=∠FAB=∠ADB=90°，∴∠FAM+∠BAD=90°，∠FAM+∠AFM=90°，∴∠BAD=∠AFM，又∵AF=AB，∴△AFM≌△BAD（AAS），∴FM=AD，∠FAM=∠ABD，故③正确，同理△ANG≌△CDA，∴NG=AD，∴FM=NG，∵FM⊥AE，NG⊥AE，∴∠FME=∠ENG=90°，∵∠AEF=∠NEG，∴△FME≌△GNE（AAS）．∴EF=EG．故④正确．故选：D．小提示：本题综合考查了全等三角形的判定与性质及等腰三角形的三线合一性质与互余、对顶角，三角形内角和等几何基础知识．熟练掌握全等三角形的判定与性质是解题的关键．4、如图，BD是△ABC的角平分线，AE⊥BD，垂足为F，若∠ABC＝35°，∠C＝50°，则∠CDE的度数为（）A ．35°B ．40°C ．45°D ．50°答案：C分析：根据角平分线的定义和垂直的定义得到∠ABD =∠EBD =12∠ABC =35°2，∠AFB =∠EFB =90°，推出AB =BE ，根据等腰三角形的性质得到AF =EF ，求得AD =ED ，得到∠DAF =∠DEF ，根据三角形的外角的性质即可得到结论． 解：∵BD 是△ABC 的角平分线，AE ⊥BD ，∴∠ABD =∠EBD =12∠ABC =35°2，∠AFB =∠EFB =90°，∴∠BAF =∠BEF ，∴AB =BE ，AE ⊥BD ，∴BD 是AE 的垂直平分线，∴AD =ED ，∴∠DAF =∠DEF ，∵∠BAC =180°-∠ABC -∠C =95°，∴∠BED =∠BAD =95°，∴∠CDE =95°-50°=45°，故选C ．小提示：本题考查了三角形的内角和，全等三角形的判定和性质，三角形的外角的性质，熟练掌握全等三角形的判定和性质是解题的关键．5、如图，△ABC ≌△DEF ，若∠A =80°,∠F =30°，则∠B 的度数是（ ）A．80°B．70°C．65°D．60°答案：B分析：由△ABC≌△DEF根据全等三角形的性质可得∠C=∠F=30°，再利用三角形内角和进行求解即可．∵△ABC≌△DEF，∴∠C=∠F，∵∠F=30°，∴∠C=30°，∵∠A=80°,∠A+∠B+∠C=180°，∴∠B=180°−∠A−∠C=70°，故选：B．小提示：本题考查了全等三角形的性质及三角形的内角和定理，熟练掌握知识点是解题的关键．6、小明同学只用两把完全相同的长方形直尺就可以作出一个角的平分线．如图：一把直尺压住射线OB，另一把直尺压住射线OA并且与第一把直尺交于点P，小明说：“射线OP就是∠BOA的角平分线．”他这样做的依据是（）A．在角的内部，到角的两边距离相等的点在角的平分线上B．角平分线上的点到这个角两边的距离相等C．三角形的三条高交于一点D．三角形三边的垂直平分线交于一点答案：A分析：过两把直尺的交点P作PF⊥BO与点F，由题意得PE⊥AO，因为是两把完全相同的长方形直尺，可得PE=PF，再根据角的内部到角的两边的距离相等的点在这个角的平分线上可得OP平分∠AOB如图所示：过两把直尺的交点P作PF⊥BO与点F，由题意得PE⊥AO，∵两把完全相同的长方形直尺，∴PE=PF，∴OP平分∠AOB（角的内部到角的两边的距离相等的点在这个角的平分线上），故选A．小提示：本题主要考查了基本作图，关键是掌握角的内部到角的两边的距离相等的点在这个角的平分线上这一判定定理．7、如图，在Rt△ABC中，∠C=90°,∠BAC的平分线交BC于点D，DE//AB，交AC于点E，DF⊥AB于点F，DE=5,DF=3，则下列结论错误的是（）A．BF=1B．DC=3C．AE=5D．AC=9答案：A分析：根据角平分线的性质得到CD=DF=3，故B正确；根据平行线的性质及角平分线得到AE=DE=5，故C正确；由此判断D正确；再证明△BDF≌△DEC，求出BF=CD=3，故A错误．解：在Rt△ABC中，∠C=90°,∠BAC的平分线交BC于点D，DF⊥AB，∴CD=DF=3，故B正确；∵DE=5，∴CE=4，∵DE//AB，∴∠ADE=∠DAF，∵∠CAD=∠BAD，∴∠CAD=∠ADE，∴AE=DE=5，故C正确；∴AC=AE+CE=9，故D正确；∵∠B=∠CDE，∠BFD=∠C=90°，CD=DF，∴△BDF≌△DEC，∴BF=CD=3，故A错误；故选：A．小提示：此题考查了角平分线的性质定理，平行线的性质，等边对等角证明角相等，全等三角形的判定及性质，熟记各知识点并综合应用是解题的关键．8、已知图中的两个三角形全等，则∠α等于（）A．72∘B．60∘C．58∘D．50∘答案：D分析：根据全等三角形的性质：全等三角形对应角相等，即可得到结论．∵图中的两个三角形全等，∠α为a和c的夹角又∵第一个三角形中a和c的夹角为50°∴∠α=50°故选：D．小提示：本题考查了全等三角形的性质，准确找到对应角是解题的关键．9、下列四个图形中，有两个全等的图形，它们是（）A．①和②B．①和③C．②和④D．③和④答案：B分析：根据全等形的概念：能够完全重合的两个图形叫做全等形可得答案．解：①和③可以完全重合，因此全等的图形是①和③．故选：B．小提示：此题主要考查了全等图形，关键是掌握全等图形的概念．AD，BD平分∠ABC，则点D到AB的距离等于( ) 10、如图，在ΔABC中，∠C=90°，AC=8，DC=13A．4B．3C．2D．1答案：C分析：如图，过点D作DE⊥AB于E，根据已知求出CD的长，再根据角平分线的性质进行求解即可.如图，过点D作DE⊥AB于E，∵AC=8，DC=1AD，3∴CD=8×1=2，1+3∵∠C=90°，BD平分∠ABC，∴DE=CD=2，即点D到AB的距离为2，故选C．小提示：本题考查了角平分线的性质，熟练掌握角平分线上的点到角两边的距离相等是解题的关键.填空题11、如图，四边形ABCD中，∠B＋∠D＝180°，AC平分∠DAB，CM⊥AB于点M，若AM＝4cm，BC＝2.5cm，则四边形ABCD的周长为_____cm．答案：13分析：过C作CE⊥AD的延长线于点E，由条件可证△AEC≌△AMC，得到AE＝AM．证明△ECD≌△MBC，由全等的性质可得DE＝MB，BC＝CD，则问题可得解．解：如图，过C作CE⊥AD的延长线于点E，∵AC平分∠BAD，∴∠EAC＝∠MAC，∵CE⊥AD，CM⊥AB，∴∠AEC＝∠AMC＝90°，CE＝CM，在Rt△AEC和Rt△AMC中，AC=AC，CE=CM，∴Rt△AEC≌Rt△AMC（HL），∴AE＝AM＝4cm，∵∠ADC＋∠B＝180°，∠ADC＋∠EDC＝180°，∴∠EDC＝∠MBC，在△EDC和△MBC中，{∠DEC=∠CMB∠EDC=∠MBCCE=CM，∴△EDC≌△MBC（AAS），∴ED＝BM，BC＝CD＝2.5cm，∴四边形ABCD的周长为AB＋AD＋BC＋CD＝AM＋BM＋AE﹣DE＋2BC＝2AM＋2BC＝8＋5＝13（cm），所以答案是：13．小提示：本题考查全等三角形的判定与性质，掌握常用的判定方法是解题的关键．12、把两个全等的三角形重合到一起，重合的顶点叫做_________，重合的边叫做_________，重合的角叫做_________．记两个三角形全等时，通常把表示_________的字母写在对应位置上．答案：对应顶点对应边对应角对应顶点分析：根据能够完全重合的两个图形叫做全等形，以及对应顶点、对应边、对应角的概念填空．解：把两个全等的三角形重合到一起，重合的顶点叫做对应顶点，重合的边叫做对应边，重合的角叫做对应角．记两个三角形全等时，通常把表示对应顶点的字母写在对应位置上．所以答案是：对应顶点；对应边；对应角；对应顶点．小提示：此题主要考查了全等形及相关概念，属于基本概念题，是需要识记的内容．13、如图，在Rt△ABC中，∠C=90°，AC=12cm，BC=6cm，一条线段PQ=AB，P，Q两点分别在AC和过点A且垂直于AC的射线AX上运动，要使△ABC和△QPA全等，则AP=_____．答案：12cm或6cm##6cm或12cm分析：当AP＝12cm或6cm时，△ABC和△PQA全等，根据HL定理推出即可．解：∵∠C＝90°，AO⊥AC，∴∠C＝∠QAP＝90°，①当AP＝6cm＝BC时，在Rt△ACB和Rt△QAP中∵{AB=PQ，BC=AP∴Rt△ACB≌Rt△QAP（HL），②当AP＝12cm＝AC时，在Rt△ACB和Rt△PAQ中{AB=PQ，AC=AP∴Rt△ACB≌Rt△PAQ（HL），所以答案是：12cm或6cm．小提示：本题考查了全等三角形的判定定理的应用，注意：判定两直角三角形全等的方法有ASA，AAS，SAS，SSS，HL．14、如图，在△ACB中，∠ACB=90°，AC=BC，点C的坐标为（﹣2，0），点B的坐标为（1，5），则A点的坐标是_____．答案：（-7，3）分析：先作辅助线AD ⊥OC 、BE ⊥OC ，通过导角证明∠CAD =∠BCE ，再证明△ADC ≌△CEB ， 得到AD 的长度(A 的纵坐标长度)、DC 长度(加上OC 得到A 横坐标长度)，根据A 点所在象限的符号，确定A 点坐标． 如图，过点A 作AD ⊥OC 于点D ，过点B 作BE ⊥OC 于点E∵ 点C 的坐标为(-2，0)，点B 的坐标为(1，5)∴ OC =2，OE =1，BE =5∵∠ACB =90°∴∠ACD +∠CAD =90°，∠ACD +∠BCE =90°∴∠CAD =∠BCE在△ADC 和△CEB 中，{∠ADC =∠BEC =90°∠CAD =∠BCE AC =BC∴△ADC ≌△CEB(AAS)∴DC =BE =5,AD =CE =1+2=3∴OD =2+5=7∴ A 点的坐标是(-7，3) ．小提示：本题考查了全等三角形的证明(在两个三角形中，如果有两组对应角，和其中一组对应角的对边分别相等，那么这两个三角形全等) ．15、如图是由九个边长为1的小正方形拼成的大正方形，图中∠1＋∠2＋∠3＋∠4＋∠5的度数为______．答案：225°分析：首先判定△ABC≌△AEF，△ABD≌△AEH，可得∠5=∠BCA，∠4=∠BDA，然后可得∠1+∠5=∠1+∠BCA=90°，∠2+∠4=∠2+∠BDA=90°，即可求得∠1+∠2+∠3+∠4+∠5的值．解：如图所示：在△ABC和△AEF中，{AB=AE∠B=∠E=90°BC=EF∴△ABC≌△AEF（SAS），∴∠5=∠BCA，∴∠1+∠5=∠1+∠BCA=90°，在Rt△ABD和Rt△AEH中，{AB=AEAD=AH∴Rt△ABD≌Rt△AEH（HL），∴∠4=∠BDA，∴∠2+∠4=∠2+∠BDA=90°，∵∠3=45°，∴∠1+∠2+∠3+∠4+∠5=90°+90°+45°=225°．所以答案是：225°．小提示：此题主要考查了全等三角形的判定和性质，关键是掌握全等三角形的性质：全等三角形对应角相等即可求解．解答题16、（1）如图，在正方形ABCD中，E、F分别是BC，CD上的点，且∠EAF=45°．直接写出BE、DF、EF之间的数量关系；（2）如图，在四边形ABCD中，AB=AD，∠B=∠D=90°，E、F分别是BC，CD上的点，且∠EAF=1∠BAD，求证：EF=BE+DF；2（3）如图，在四边形ABCD中，AB=AD，∠B+∠ADC=180°，延长BC到点E，延长CD到点F，使得∠BAD，则结论EF=BE+DF是否仍然成立？若成立，请证明；不成立，请写出它们的数量关系并∠EAF=12证明．答案：（1）EF=BE+DF，理由见详解；（2）见详解；（3）结论EF＝BE＋FD不成立，应当是EF＝BE−FD．理由见详解．分析：（1）在CD的延长线上截取DM＝BE，连接AM，证出△ABE≌△ADM，根据全等三角形的性质得出BE＝DM，再证明△AEF≌△AMF，得EF＝FM，进而即可得出答案；（2）在CD的延长线上截取DG＝BE，连接AG，证出△ABE≌△ADG，根据全等三角形的性质得出BE＝DG，再证明△AEF≌△AGF，得EF＝FG，即可得出答案；（3）按照（2）的思路，我们应该通过全等三角形来实现相等线段的转换．就应该在BE上截取BG，使BG＝DF，连接AG．根据（2）的证法，我们可得出DF＝BG，GE＝EF，那么EF＝GE＝BE−BG＝BE−DF．所以（1）的结论在（3）的条件下是不成立的．（1）解：EF=BE+DF，理由如下：延长CD，使DM=BE，连接AM，∵在正方形ABCD中，AB=AD，∠B=∠ADM=90°，∴△ABE≌△ADM，∴∠BAE=∠DAM，AE=AM，∵∠EAF=45°，∴∠BAE+∠DAF=∠DAM+∠DAF =90°-45°=45°，∴∠EAF=∠MAF=45°，又∵AF=AF，AE=AM，∴△AEF≌△AMF，∴EF=MF=MD+DF=BE+DF；（2）在CD的延长线上截取DG＝BE，连接AG，如图，∵∠ADF＝90°，∠ADF＋∠ADG＝180°，∴∠ADG＝90°，∵∠B＝90°，∴∠B＝∠ADG＝90°，∵BE＝DG，AB＝AD，∴△ABE≌△ADG（SAS），∴∠BAE＝∠DAG，AG＝AE，∴∠EAG＝∠EAD＋∠DAG＝∠EAD＋∠ABE＝∠BAD，∵∠EAF=1∠BAD，2∴∠EAF=1∠EAG,2∴∠EAF＝∠FAG，又∵AF＝AF，AE＝AG，∴△AEF≌△AGF（SAS），∴EF＝FG＝DF＋DG＝EB＋DF；（3）结论EF＝BE＋FD不成立，应当是EF＝BE−FD．理由如下：如图，在BE上截取BG，使BG＝DF，连接AG．∵∠B ＋∠ADC ＝180°，∠ADF ＋∠ADC ＝180°，∴∠B ＝∠ADF ．∵在△ABG 与△ADF 中，{AB =AD∠ABG =∠ADF BG =DF，∴△ABG ≌△ADF （SAS ）．∴∠BAG ＝∠DAF ，AG ＝AF ．∴∠BAG ＋∠EAD ＝∠DAF ＋∠EAD ＝∠EAF ＝12∠BAD =12∠GAF ． ∴∠GAE ＝12∠BAD =∠EAF ．∵AE ＝AE ，AG ＝AF ．∴△AEG ≌△AEF ．∴EG ＝EF ，∵EG ＝BE −BG∴EF ＝BE −FD ．小提示：本题考查了三角形综合题，三角形全等的判定和性质等知识，解题的关键是学会利用旋转变换的思想添加辅助线，构造全等三角形解决问题，解题时注意一些题目虽然图形发生变化，但是证明思路和方法是类似的，属于中考压轴题．17、（1）如图1，已知△ABC 中，∠BAC =90°，AB =AC ，直线m 经过点A,BD ⊥直线m ，CE ⊥直线m ，垂足分别为点D,E ．求证：DE =BD +CE ．（2）如图2，将（1）中的条件改为：在△ABC 中，AB =AC,D,A,E 三点都在直线m 上，并且有∠BDA =∠AEC=∠BAC．请写出DE,BD,CE三条线段的数量关系，并说明理由．答案：（1）证明见解析；（2）DE=BD+CE，证明见解析分析：（1）利用已知得出∠CAE=∠ABD，进而利用AAS得出则△ABD≌△CAE，即可得出DE=BD+CE；（2）根据∠BDA=∠AEC=∠BAC，得出∠CAE=∠ABD，在△ADB和△CEA中，根据AAS证出△ADB≌△CEA，从而得出AE=BD，AD=CE，即可证出DE=BD+CE；（1）DE=BD+CE．理由如下：∵BD⊥m，CE⊥m，∴∠BDA=∠AEC=90°又∵∠BAC=90°，∴∠BAD+∠CAE=90°，∠BAD+∠ABD=90°，∴∠CAE=∠ABD在△ABD和△CAE中，{∠ABD＝∠CAE∠ADB＝∠CEA＝90°AB＝AC，∴△ABD≌△CAE（AAS）∴BD=AE，AD=CE，∵DE=AD+AE，∴DE=CE+BD；（2）DE=BD+CE，理由如下：∵∠BDA=∠AEC=∠BAC，∴∠DBA +∠BAD =∠BAD +∠CAE ，∴∠CAE =∠ABD ，在△ADB 和△CEA 中，{∠ABD ＝∠CAE∠ADB ＝∠CEA AB ＝AC，∴△ADB ≌△CEA （AAS ），∴AE =BD ，AD =CE ，∴BD +CE =AE +AD =DE ；小提示：本题考查了全等三角形的判定与性质综合中的“一线三等角”模型：判定三角形全等的方法有“SSS ”、“SAS ”、“ASA ”、“AAS ”；全等三角形的对应边相等．也考查了等边三角形的判定与性质．18、如图，在五边形ABCDE 中，AB =CD ，∠ABC =∠BCD ，BE ，CE 分别是∠ABC ，∠BCD 的角平分线．(1)求证：△ABE ≌△DCE ；(2)当∠A =80°，∠ABC =140°，时，∠AED =_________度(直接填空)．答案：(1)见解析；(2)100分析：（1）根据∠ABC =∠BCD ，BE ，CE 分别是∠ABC ，∠BCD 的角平分线，可得∠ABE =∠DCE ，∠CBE =∠BCE ，推出BE =CE ，由此利用SAS 证明△ABE ≌△DCE ；（2）根据三角形全等的性质求出∠D 的度数，利用公式求出五边形的内角和，即可得到答案．（1）证明：∵∠ABC =∠BCD ，BE ，CE 分别是∠ABC ，∠BCD 的角平分线，∴∠ABE =∠CBE =12∠ABC ，∠BCE =∠DCE =12∠BCD ，∴∠ABE =∠DCE ，∠CBE =∠BCE ，∴BE=CE，又∵AB=CD，∴△ABE≌△DCE（SAS）；（2）∵△ABE≌△DCE，∴∠D=∠A=80°，∵五边形ABCDE的内角和为(5−2)×180°=540°，∴∠AED=540°−80°×2−140°×2=100°，所以答案是：100．小提示：此题考查了全等三角形的判定及性质，多边形内角和计算，正确掌握全等三角形的判定及性质定理是解题的关键．。

2021
10
模型四 一线三垂直型 模型解读：基本图形如下：此类图形 通常告诉 BD⊥DE，AB⊥AC， CE⊥DE，那么一定有∠B＝∠CAE.（常用到同（等）角的余角相等）
2021
11
4．如图，AD⊥AB于A，BE⊥AB于B，点C在AB上，且CD⊥CE，CD＝CE. 求证：AB＝AD＋BE.
2021
2021
3
1．如图，AB∥DE，AC∥DF，BE＝CF，求证：AB＝DE.
2021
4
解：∵BE＝CF，∴BE＋EC＝CF＋EC，即 BC＝EF， ∵AB∥DE，AC∥DF，∴∠B＝∠DEF，∠ACB＝∠F， 在△ABC 与△DEF 中 ∠B＝∠DEF， BC＝EF， ∠ACB＝∠F， ∴△ABC≌△DEF(ASA) ∴AB＝DE
2021
8
3．如图，AB⊥CD于B，CF交AB于E，CE＝AD，BE＝BD.求证：CF⊥AD.
2021
9
解：∵AB⊥CD，∴∠EBC＝∠DBA＝90°.在 Rt△CEB 与 Rt△ADB 中 CBEE＝ ＝ABDD，，∴Rt△CEB≌Rt△ADB(HL)，∴∠C＝∠A，又∵∠C＋∠CEB＝ 90°，∠CEB＝∠AEF，∴∠A＋∠AEF＝90°，∴CF⊥AD
12
解：∵AD⊥AB，BE⊥AB，CD⊥CE，∴∠DAC＝∠CBE＝∠DCE＝90 °，又∵∠DCB＝∠D＋∠DAC＝∠DCE＋∠ECB，∴∠D＝∠ECB.在△ACD
与△BEC 中，∠∠AD＝＝∠∠BEC，B，∴△ACD≌△BEC(AAS)，∴AC＝BE，CB＝ DC＝CE，
AD，∴AB＝AC＋CB＝AD＋BE
2021
5
模型二 翻折型 模型解读：将原图形沿着某一条直线折叠后，直线两边的部分能够完全重 合，这两个三角形称之为翻折型全等三角形．此类图形中要注意其隐含条件， 即公共边或公共角相等．

人教版八年级数学全等三角形的常见模型总结全等三角形的常见模型总结全等三角形是数学中的一个重要概念，它代表着两个三角形的所有对应部分完全相等。

在八年级数学教材中，全等三角形的学习是一个重要的内容。

本文将对人教版八年级数学中常见的全等三角形模型进行总结。

一、三个已知条件1. SAS（边角边）判定法SAS判定法是指如果两个三角形的两边和夹角分别相等，则这两个三角形全等。

这个模型通常用于根据已知条件构造全等三角形。

例如，已知△ABC和△DEF，已知AB=DE，BC=EF，∠B=∠E，要求证明△ABC≌△DEF。

2. ASA（角边角）判定法ASA判定法是指如果两个三角形的两角和一边分别相等，则这两个三角形全等。

这个模型常用于证明两个三角形全等。

例如，已知△ABC和△DEF，已知∠A=∠D，∠B=∠E，AB=DE，要求证明△ABC≌△DEF。

3. SSS（边边边）判定法SSS判定法是指如果两个三角形的三边分别相等，则这两个三角形全等。

这个模型常用于证明两个三角形全等。

例如，已知△ABC和△PQR，已知AB=PQ，BC=QR，AC=PR，要求证明△ABC≌△PQR。

二、全等三角形的性质1. 对应部分相等对应的顶点、边和夹角都相等。

2. 全等三角形的性质相等全等三角形的各个角、边的性质都相等，比如角平分线和中线相等、高和中线相等等。

三、应用实例1. 建筑几何模型全等三角形在建筑几何中有着广泛的应用。

例如，在建造房屋的过程中，根据所给定的尺寸，可以通过构造全等三角形来确定某些未知尺寸，确保建筑物的稳定性和均衡性。

2. 测量和导航全等三角形在测量和导航中也有着重要的应用。

例如，在测量高楼大厦时，可以通过测量一些已知长度和角度，利用全等三角形模型来计算难以测量的高度。

在导航中，利用全等三角形的性质可以确定船只或飞机的位置和方向。

3. 几何证明全等三角形的模型在几何证明中也是常见的。

许多几何定理的证明需要利用全等三角形构造相等的边或角来推导。

常见全等三角形模型（压轴）三角形全等的判定方法：三边分别相等的两个三角形全等（可以简写成“边边边”或“SSS”）．两边和它们的夹角分别相等的两个三角形全等（可以简写成“边角边”或“SAS”）．两角和它们的夹边分别相等的两个三角形全等（可以简写成“角边角”或“ASA”）．两角和其中一个角的对边分别相等的两个三角形全等（可以简写成“角角边”或“AAS”）．斜边和一条直角边分别相等的两个直角三角形全等（可以简写成“斜边、直角边”或“HL”）．证明三角形全等的基本思路：全等三角形中常见的基本模型：1手拉手模型①△ABE和△ACF均为等边三角形结论：（1）△ABF≌△AEC；（2）∠BOE =60°；（3）OA平分∠EOF ．拓展图形：结论：（1）AD=BE ；（2）∠ACB=∠AOB ；（3）△PCQ为等边三角形；（4）PQ∥AE ；（5）AP=BQ ；（6）CO平分∠AOE ；（7）OA=OB+OC；（8）OE=OC+OD．②△ABD和△ACE均为等腰直角三角形结论：（1）BE=CD；（2）BE⊥CD ．③ABEF和ACHD均为正方形结论：（1）BD⊥CF；（2）BD=CF．2三垂直模型由△AEB≌△BDC导出由△ABE≌△BCD导出由△ABE≌△ECD导出AE=CD+DE AB=EC+CD BC=AB+CD3等腰直角三角形型定点是斜边中点，BF=AE（AF=CE），动点在两直角边上滚动的旋转全等：结论：（1）△BDF≌△ADE，△ADF≌△CDE；（2）DE⊥DF；（3）S四边形AFDE=1/2S△ABC．例1．在直线ABC的同一侧作两个等边三角形△ABD和△BCE，连接AE与CD，证明：（1）△ABE≌△DBC；（2）AE=DC；（3）AE与DC的夹角为60°；（4）BH平分∠AHC；（5）△ABG≌△DBF；（6）等边△GBF；（7）GF∥AC.1．以点A为顶点作两个等腰直角三角形（△ABC，△ADE），如图1所示放置，使得一直角边重合，连接BD，CE．（1）说明BD=CE；（2）延长BD，交CE于点F，求∠BFC的度数；（3）若如图2放置，上面（1），（2）中的结论还成立吗？请简单说明理由．2．已知△ABC为等边三角形，点D为直线BC上的一动点（点D不与B、C重合），以AD为边作等边△ADE（顶点A、D、E按逆时针方向排列），连接CE．（1）如图1，当点D在边BC上时，求证：①BD=CE，②AC=CE+CD；（2）如图2，当点D在边BC的延长线上且其他条件不变时，结论AC=CE+CD是否成立？若不成立，请写出AC、CE、CD之间存在的数量关系，并说明理由；（3）如图3，当点D在边BC的反向延长线上且其他条件不变时，补全图形，并直接写出AC、CE、CD之间存在的数量关系．3．如图，在平面直角坐标系中，点A的坐标是（a，0）（a＞0），点C是y轴上的一个动点，点C在y轴上移动时，始终保持△ACP是等边三角形，当点C移动到点O时，得到等边△AOB（此时点P与点B重合）．（1）点C在移动的过程中，当等边三角形ACP的顶点P在第三象限时（如图所示），求证：△AOC≌△ABP；（2）若点P在第三象限，BP交x轴于点E，且∠ACO＝20°，求∠P AE的度数和E 点的坐标；（3）点C 在y 轴移动的过程中，若∠APB ＝30°，则点P 的横坐标为 ． 例2．如图1，OA ＝1，OB ＝3，以A 为直角顶点，AB 为腰在第三象限作等腰Rt △ABC ． （1）求点C 的坐标； （2）如图2，P 为y 轴负半轴上的一个动点，当点P 向下运动时，以P 点为直角顶点，P A 为腰作等腰Rt △APQ ，过Q 作QE ⊥x 轴于E 点，求PO ﹣QE 的值．1．如图，AE ⊥AB 且AE=AB ，BC ⊥CD 且BC=CD ，请按照图中所标注的数据，计算图中实线所围成的图形的面积S 是（ ）．A ．50B ．62C ．65D ．682．直线CD 经过的顶点C ，CA=CB ．E 、F 分别是直线CD 上两点，且．（1）若直线CD 经过的内部，且E 、F 在射线CD 上，请解决下面两个问题： ①如图1，若90,90BCA α∠=∠=，则 （填“”，“”或“”号）；②如图2，若，若使①中的结论仍然成立，则 与 应满足的关系是 ；（2）如图3，若直线CD 经过的外部，，请探究EF 、与BE 、AF 三条线段的数量关系，并给予证明．3．（1）如图1，OA ＝3，OB ＝6，以点A 为顶点，AB 为腰在第三象限作等腰直角△ABC ，则C 点的坐标为 ；（2）如图2，OA ＝3，P 为y 轴负半轴上的一个动点，若以P 为直角顶点，P A 为腰作等腰直角△APD ，过D 作DE ⊥x 轴于E 点，求OP ﹣DE 的值；（3）如图3，点F 坐标为（﹣3，﹣3），点G （0，m ）在y 轴负半轴上，点H （n ，0）在x 轴的正半轴上，且FH ⊥FG ，求m +n 的值．4．如图，在平面直角坐标系中，△ABC 的顶点A 在y 轴上，顶点C 在x 轴上，∠BAC=90°，AB=AC ，点E 为边AC 上一点，连接BE 交y 轴于点F ，交x 轴于点G ，作CD ⊥BE 交BCA ∠BEC CFA α∠=∠=∠BCA ∠EF BE AF -><=0180BCA <∠<α∠BCA ∠BCA ∠BCA α∠=∠A B CEF D D A BC E F AD F CE B 图1 图2 图3BE延长线于点D，且CD=BF，连接AD，CF.（1）求证：△ABF≌△ACD；（2）若∠ACF=2∠CBF，求证：∠ACO=∠FCO；（3）在（2）的条件下，若点A的坐标为（0，2），求OC的长.5．已知：如图所示，在△ABC中，AB=AC，∠BAC=90°，D为AC中点，AF⊥BD 于E，交BC于F，连接DF．求证：∠ADB=∠CDF．例3．如图1，点P、Q分别是边长为4cm的等边ABC∆边AB、BC上的动点，点P从顶点A向点B运动，点Q从顶点B同时出发向点C运动，且它们的速度都为1/cm s，∠变化吗？若变化，则（1）连接AQ、CP交于点M，则在P、Q运动的过程中，CMQ说明理由，若不变，则求出它的度数；∆是直角三角形？（2）何时PBQ（3）如图2，若点P、Q在运动到终点后继续在射线AB、BC上运动，直线AQ、CP ∠变化吗？若变化，则说明理由，若不变，则求出它的度数．交点为M，则CMQ1．如图，点G、H分别是正六边形ABCDEF的边BC、CD上的点，且BG＝CH，AG 交BH于点P．（1）求证：△ABG≌△BCH；（2）求∠APH的度数．例4．如图，Rt△ABC中，AB=AC，∠BAC=90°，点O是BC的中点，如果点M、N 分别在线段AB、AC上移动，并在移动过程中始终保持AN=BM．（1）求证：△ANO≌△BMO；（2）求证：OM⊥ON．（3）当M、N分别在线段AB、AC上移动时，四边形AMON的面积如何变化？1．如图所示，△ABC是等腰直角三角形，∠BAC=90°，AB=AC．（1）若D为BC的中点，过D作DM⊥DN分别交AB．AC于M．N，求证：DM=DN；（2）若DM⊥DN分别和BA．AC延长线交于M．N，问DM和DN有何数量关系，并证明．2．将一副三角板按如图所示的方式摆放，AD是等腰直角三角板ABC斜边BC上的高，另一块三角板DMN的直角顶点与点D重合，DM、DN分别交AB、AC于点E、F．（1）请判别△DEF的形状．并证明你的结论；（2）若BC＝4，求四边形AEDF的面积．。

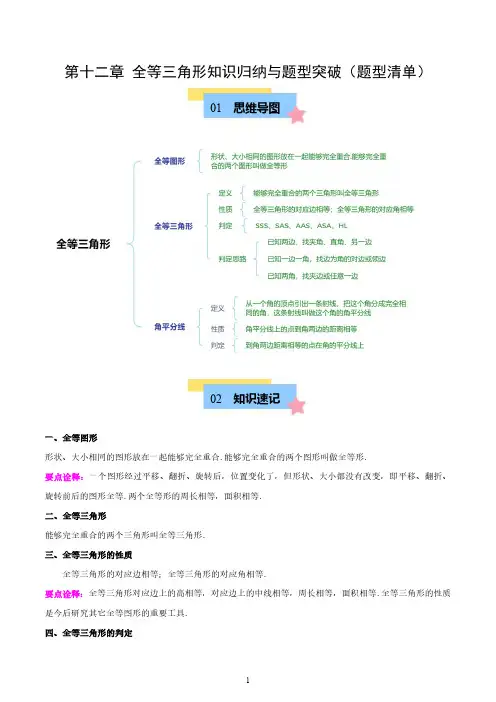
第十二章全等三角形知识归纳与题型突破（题型清单）01思维导图02知识速记一、全等图形形状、大小相同的图形放在一起能够完全重合.能够完全重合的两个图形叫做全等形.要点诠释：一个图形经过平移、翻折、旋转后，位置变化了，但形状、大小都没有改变，即平移、翻折、旋转前后的图形全等.两个全等形的周长相等，面积相等.二、全等三角形能够完全重合的两个三角形叫全等三角形.三、全等三角形的性质全等三角形的对应边相等；全等三角形的对应角相等.要点诠释：全等三角形对应边上的高相等，对应边上的中线相等，周长相等，面积相等.全等三角形的性质是今后研究其它全等图形的重要工具.四、全等三角形的判定五、全等三角形的证明思路SAS HL SSS AAS SAS ASA AAS ASA AAS⎧→⎧⎪⎪→⎨⎪⎪⎪→⎩⎪⎪→→⎧⎪⎪→⎧⎪⎪⎨⎨⎪→⎨⎪⎪⎪⎪⎪→⎩⎩⎪⎪→⎧⎪⎨→⎪⎩⎪⎩找夹角已知两边找直角找另一边边为角的对边找任一角找夹角的另一边已知一边一角边为角的邻边找夹边的另一角找边的对角找夹边已知两角找任一边六、全等三角形证明方法全等三角形是平面几何内容的基础，这是因为全等三角形是研究特殊三角形、四边形、相似图形、圆等图形性质的有力工具，是解决与线段、角相关问题的一个出发点.运用全等三角形，可以证明线段相等、线段的和差倍分关系、角相等、两直线位置关系等常见的几何问题.可以适当总结证明方法.1．证明线段相等的方法：(1)证明两条线段所在的两个三角形全等.(2)利用角平分线的性质证明角平分线上的点到角两边的距离相等.(3)等式性质.2．证明角相等的方法：(1)利用平行线的性质进行证明.(2)证明两个角所在的两个三角形全等.(3)利用角平分线的判定进行证明.(4)同角（等角）的余角（补角）相等.(5)对顶角相等.3．证明两条线段的位置关系（平行、垂直）的方法；可通过证明两个三角形全等，得到对应角相等，再利用平行线的判定或垂直定义证明.4．辅助线的添加:(1)作公共边可构造全等三角形；(2)倍长中线法；(3)作以角平分线为对称轴的翻折变换全等三角形；(4)利用截长(或补短)法作旋转变换的全等三角形.5.证明三角形全等的思维方法:（1）直接利用全等三角形判定和证明两条线段或两个角相等，需要我们敏捷、快速地发现两条线段和两个角所在的两个三角形及它们全等的条件.（2）如果要证明相等的两条线段或两个角所在的三角形全等的条件不充分时，则应根据图形的其它性质或先证明其他的两个三角形全等以补足条件.（3）如果现有图形中的任何两个三角形之间不存在全等关系，此时应添置辅助线，使之出现全等三角形，通过构造出全等三角形来研究平面图形的性质.七、角平分线概念：从一个角的顶点引出一条射线，把这个角分成完全相同的角，这条射线叫做这个角的角平分线。

8年级上册数学模型由于您没有给出具体的8年级上册数学题目内容，我将以人教版八年级上册数学中的一些常见模型为基础为您整理学习资料：一、三角形模型。

1. 全等三角形模型。

- 平移型。

- 特征：两个三角形通过平移得到全等关系。

例如，在三角形ABC和三角形DEF 中，如果AB平行且等于DE，BC平行且等于EF，AC平行且等于DF，那么三角形ABC≌三角形DEF（SSS全等判定）。

- 解题要点：找到对应边相等的关系，通常可以通过平行四边形的性质（对边相等）来辅助证明。

- 旋转型。

- 特征：一个三角形绕着某个点旋转一定角度后与另一个三角形全等。

三角形ABC绕点O旋转一定角度后得到三角形A'B'C'，如果OA = OA'，OB = OB'，OC = OC'，且∠AOA'=∠BOB' = ∠COC'，可以通过SAS（边角边）等全等判定定理来证明全等。

- 解题要点：确定旋转中心和旋转角度，找出对应边和对应角相等的关系。

- 翻折型。

- 特征：将一个三角形沿着某条直线翻折得到与另一个三角形全等。

例如，三角形ABC沿直线l翻折得到三角形A'B'C'，则对应边AB = A'B'，BC = B'C'，AC =A'C'，对应角∠A=∠A'，∠B = ∠B'，∠C = ∠C'。

- 解题要点：找出对称轴，利用对称轴两侧的图形对称性质，即对应点到对称轴的距离相等，对应线段相等，对应角相等。

2. 等腰三角形模型。

- 三线合一模型。

- 定义：等腰三角形底边上的高、底边上的中线、顶角平分线互相重合。

- 应用：已知等腰三角形的某条线段是底边上的高、中线或者顶角平分线中的一条，就可以得出它同时具备另外两条线段的性质。

例如，在等腰三角形ABC中，AB = AC，AD是BC边上的高，那么AD也是BC边上的中线和∠BAC的平分线。

A. ①④
B.①②
C.②③
D.③④
2．如图，ABD ≌ CDB ，且 AB 和 CD 是对应边，下面四个结论中不正确的是（ ）
A. ABD和CDB 的面积相等
A
D
B. ABD和CDB 的周长相等 C. A + ABD = C + CBD
B
C
D.DAD//BC 且 AD=BC
3．如图， ABC ≌ BAD ，A 和 B 以及 C 和 D 分别是对应点，如果
4．全等三角形的判定（一）：三边对应相等的两个三角形全等，简与成“边边边”或“SSS”．
AB = DE 如图，在 ABC 和 DEF 中 BC = EF
AC =
【典型例题】
例1．如图， ABC ≌ ADC ，点 B 与点 D 是对应点， BAC = 26 ，且 B = 20 ， SABC = 1，求 CAD , D, ACD 的度数及 ACD 的面积．
数及 BC 的长．
E
F
A
BC
D
本文来源于网络，如果侵权行为，请联系删除！
精品文档，助力人生，欢迎关注小编！
11．如图，在 ABC与ABD 中，AC=BD，AD=BC，求证： ABC ≌ ABD
D A
C B
全等三角形（一）作业
1．如图， ABC ≌ CDA ，AC=7cm，AB=5cm.，则 AD 的长是（ ）
求证：（1） DE ⊥ AB ； （2）BD 平分 ABC （角平分线的相关证明及性质）
B
A E
D
C
【巩固练习】 1．下面给出四个结论：①若两个图形是全等图形，则它们形状一定相同；②若两个图形的
形状相同，则它们一定是全等图形；③若两个图形的面积相等，则它们一定是全等图形； ④若两个图形是全等图形，则它们的大小一定相同，其中正确的是（ ）

类型 4 三垂直模型
在三垂直模型中，利用余角的性质寻求两个直角三角形中的一 组锐角相等，再加上任意一组对应边相等，易证两个直角三角形全 等，常见的模型如下：
4.在△ABC 中，∠ACB＝90°，AC＝BC，直线 MN 经过点 C， 且 AD⊥MN 于点 D，BE⊥MN 于点 E.
(1)当直线 MN 绕点 C 旋转到图 1 的位置时，试问 DE，AD，BE 具有怎样的等量关系？并加以证明.
②AE⊥BD． 证明：②∵△ACE≌△BCD，∴∠CAE＝∠CBD． ∵∠CAE＋∠EAB＋∠ABC＝90°， ∴∠CBD＋∠EAB＋∠ABC＝90°
∴∠AFB＝90°.∴AE⊥BD．
(2)如图 2，当 α＝60°时，直接写出∠AFB 的度数为 60° . (3)如图 3，直接写出∠AFD 的度数为 180°－α (用含 α 的式 子表示).
(2)若∠ADO＝35°，求∠DOC 的度数. 解：∵△AOD≌△OBC，∴∠ADO＝∠OCB＝35°. ∵OD∥BC，∴∠DOC＝∠OCB＝35°.
类型 2 对称模型
2.如图，∠1＝∠2，∠3＝∠4，求证：AD＝CD． 证明：∵∠3＝∠4， ∴∠BEA＝∠BEC． 又∵BE＝BE，∠1＝∠2， ∴△BAE≌△BCE(ASA). ∴AE＝CE. 又∵∠3＝∠4，ED＝ED，
解：结论 DE＝BD＋CE 成立. 证明：∵∠BDA＝∠BAC＝α， ∴∠DBA＋∠BAD＝∠BAD＋∠CAE＝180°－α. ∴∠ABD＝∠CAE.
又∵∠BDA＝∠AEC，AB＝CA， ∴△ADB≌△CEA(AAS). ∴BD＝AE，AD＝CE. ∴DE＝AE＋AD＝BD＋CE.
第十二章 全等三角形
小专题(五) 全等三角形的基本模型
类型 1 平移模型

人教版八年级数学全等三角形的常见模型总结(精选.)人教版八年级数学全等三角形常见模型总结要点梳理：全等三角形的判定与性质：一般三角形：边角边（SAS）、判角边角（ASA）、定角角边（AAS）、边边边（SSS）。

直角三角形：斜边、直角边定理（HL）。

性质：对应边相等，对应角相等（其他对应元素也相等，如对应边上的垂高相等）。

备判定：三角形全等必须有一组对应边相等。

注类型一：角平分线模型应用1.角平分性质模型：利用角平分线的性质。

例题解析：例1：如图1，在△ABC中，∠C=90°，AD平分∠CAB，BC=6cm，BD=4cm，那么点D到直线AB的距离是多少？答案】作DE⊥XXX于点E，DE=3cm。

例2：如图2，已知，∠1=∠2，∠3=∠4，求证：AP平分∠BAC。

答案】如图2，由角平分线的性质可知，PM=PN，PN=PQ，故PM=PQ，又因为PA是角BAC的平分线，所以XXX平分∠BAC。

类型二：角平分线模型应用2.角平分线，分两边，对称全等（截长补短构造全等）。

例题解析：例1：在△ABC中，∠BAC=60°，∠C=40°，AP平分∠XXX于P，BQ平分∠XXX于Q，求证：AB+BP=BQ+AQ。

答案】如图1，过O作OD∥BC交AB于D，∠ADO=∠ABC=180°－60°－40°=80°，又∵∠AQO=∠C+∠QBC=80°，∴∠ADO=∠AQO，又∵∠DAO=∠QAO，OA=AO，∴△ADO≌△AQO，∴OD=OQ，AD=AQ，又因为OD∥BP，所以∠PBO=∠DOB，又∠PBO=∠DBO，∴∠DBO=∠DOB，∴BD=OD，又∵∠XXX∠C+∠PAC=70°，∠BOP=∠OBA+∠BAO=70°，∴∠BOP=∠BPO，∴BP=OB，∴AB+BP=AD+DB+BP=AQ+OQ+BO=AQ+BQ。

如图，将△ADE逆时针旋转60°，使△ADE≌△ABC，从而得到△MDE≌△MAC，因为M为BD的中点，所以ME=MC，因此△EMC为等腰三角形，且∠MDE=∠MAC=30°，所以△EMC为等腰直角三角形。

专题06模型构建专题：全等三角形中的常见解题模型模型构建一四边形中构造全等三角形解题模型构建二一线三等角模型模型构建三三垂直模型模型构建四倍长中线模型模型构建一四边形中构造全等三角形解题例题：（2021·天津·耀华中学八年级期中）如图，在四边形ABCD中，AB＝CB，AD＝CD．求证∠C＝∠A．【答案】见解析【解析】【分析】先连接BD，由AB＝CB、AD＝CD、BD=BD可证∠ABD∠∠CBD，即可证得结论．【详解】证明：如图：连接BD，∠在∠ABD和∠CBD中，AB BCAD CDBD BD=⎧⎪=⎨⎪=⎩∠∠ABD∠∠CBD，∠∠C＝∠A．【点睛】本题主要考查了全等三角形的判定与性质，正确作出辅助线、灵活运用SSS 证明三角形全等是解答本题的关键．【变式训练】1．（2022·山东济宁·八年级期末）如图，在四边形ABCD 中，CB AB ⊥于点B ，CD AD ⊥于点D ，点E ，F 分别在AB ，AD 上，AE AF =，CE CF =．(1)若8AE =，6CD =，求四边形AECF 的面积；(2)猜想∠DAB ，∠ECF ，∠DFC 三者之间的数量关系，并证明你的猜想．【答案】(1)48(2)∠DAB ＋∠ECF ＝2∠DFC ，证明见解析【解析】【分析】（1）连接AC ，证明∠ACE ∠∠ACF ，则S △ACE ＝S △ACF ，根据三角形面积公式求得S △ACF 与S △ACE ，根据S 四边形AECF ＝S △ACF ＋S △ACE 求解即可；（2）由∠ACE ∠∠ACF 可得∠FCA ＝∠ECA ，∠F AC ＝∠EAC ，∠AFC ＝∠AEC ，根据垂直关系，以及三角形的外角性质可得∠DFC ＋∠BEC ＝∠FCA ＋∠F AC ＋∠ECA ＋∠EAC ＝∠DAB ＋∠ECF ．可得∠DAB ＋∠ECF ＝2∠DFC(1)解：连接AC ，如图，在∠ACE和∠ACF中AE AF CE CF AC AC=⎧⎪=⎨⎪=⎩∠∠ACE ∠∠ACF（SSS）．∠S△ACE＝S△ACF，∠F AC＝∠EAC．∠CB∠AB，CD∠AD，∠CD＝CB＝6．∠S△ACF＝S△ACE＝12AE·CB＝12×8×6＝24．∠S四边形AECF＝S△ACF＋S△ACE＝24＋24＝48．(2)∠DAB＋∠ECF＝2∠DFC证明：∠∠ACE ∠∠ACF，∠∠FCA＝∠ECA，∠F AC＝∠EAC，∠AFC＝∠AEC．∠∠DFC与∠AFC互补，∠BEC与∠AEC互补，∠∠DFC＝∠BEC．∠∠DFC＝∠FCA＋∠F AC，∠BEC＝∠ECA＋∠EAC，∠∠DFC＋∠BEC＝∠FCA＋∠F AC＋∠ECA＋∠EAC＝∠DAB＋∠ECF．∠∠DAB＋∠ECF＝2∠DFC【点睛】本题考查了三角形全等的性质与判定，三角形的外角的性质，掌握三角形全等的性质与判定是解题的关键．2．（2022·福建·漳州实验中学七年级阶段练习）在四边形ABDC中，AC=AB，DC=DB，∠CAB=60°，∠CDB=120°，E是AC上一点，F是AB延长线上一点，且CE=BF．(1)试说明：DE=DF：(2)在图中，若G在AB上且∠EDG=60°，试猜想CE，EG，BG之间的数量关系并证明所归纳结论．(3)若题中条件“∠CAB=60°，∠CDB=120°改为∠CAB=α，∠CDB=180°﹣α，G在AB上，∠EDG满足什么条件时，（2）中结论仍然成立？【答案】(1)见解析；(2)CE+BG=EG，理由见解析；(3)当∠EDG =90°-12α时，（2）中结论仍然成立．【解析】【分析】（1）首先判断出C DBF ∠=∠，然后根据全等三角形判定的方法，判断出ΔΔCDE BDF ≅，即可判断出DE DF =．（2）猜想CE 、EG 、BG 之间的数量关系为：CE BG EG +=．首先根据全等三角形判定的方法，判断出ABD ACD ∆≅∆，即可判断出60BDA CDA ∠=∠=︒；然后根据60EDG ∠=︒，可得CDE ADG ∠=∠，ADE BDG ∠=∠，再根据CDE BDF ∠=∠，判断出EDG FDG ∠=∠，据此推得ΔΔDEG DFG ≅，所以EG FG =，最后根据CE BF =，判断出CE BG EG +=即可．（3）根据（2）的证明过程，要使CE BG EG +=仍然成立，则12EDG BDA CDA CDB ∠=∠=∠=∠，即11(180)9022EDG αα∠=︒-=︒-，据此解答即可． (1)证明：360CAB C CDB ABD ∠+∠+∠+∠=︒，60CAB ∠=︒，120CDB ∠=︒，36060120180C ABD ∴∠+∠=︒-︒-︒=︒，又180DBF ABD ∠+∠=︒，C DBF ∴∠=∠，在CDE ∆和BDF ∆中，CD BD C DBF CE BF =⎧⎪∠=∠⎨⎪=⎩ΔΔ()CDE BDF SAS ∴≅，DE DF ∴=．(2)解：如图，连接AD ，猜想CE 、EG 、BG 之间的数量关系为：CE BG EG +=．证明：在ABD ∆和ACD ∆中，AB AC BD CD AD AD =⎧⎪=⎨⎪=⎩，ΔΔ()ABD ACD SSS ∴≅，111206022BDA CDA CDB ∴∠=∠=∠=⨯︒=︒， 又60EDG ∠=︒，CDE ADG ∴∠=∠，ADE BDG ∠=∠，由（1），可得ΔΔCDE BDF ≅，CDE BDF ∴∠=∠，60BDG BDF ∴∠+∠=︒，即60FDG ∠=︒，EDG FDG ∴∠=∠，在DEG ∆和DFG ∆中，DE DF EDG FDG DG DG =⎧⎪∠=∠⎨⎪=⎩ΔΔ()DEG DFG SAS ∴≅，EG FG ∴=，又CE BF =，FG BF BG =+，CE BG EG ∴+=；(3)解：要使CE BG EG +=仍然成立， 则12EDG BDA CDA CDB ∠=∠=∠=∠， 即11(180)9022EDG αα∠=︒-=︒-， ∴当1902EDG α∠=︒-时，CE BG EG +=仍然成立． 【点睛】本题综合考查了全等三角形的性质和判定，此题是一道综合性比较强的题目，有一定的难度，能根据题意推出规律是解此题的关键．模型构建二 一线三等角模型例题：（2022·全国·八年级专题练习）如图，在ABC 中，240AB AC B ==∠=︒，，点D 在线段BC 上运动（D 不与B 、C 重合），连接AD ，作40ADE ∠=︒，DE 交线段AC 于E ．(1)点D 从B 向C 运动时，BDA ∠逐渐变__________（填“大”或“小”），但BDA ∠与EDC ∠的度数和始终是__________度．(2)当DC 的长度是多少时，ABD DCE △△≌，并说明理由．【答案】(1)小；140(2)当DC =2时，∠ABD ∠∠DCE ，理由见解析【解析】【分析】（1）利用三角形的内角和即可得出结论；（2）当DC =2时，利用∠DEC +∠EDC =140°，∠ADB +∠EDC =140°，求出∠ADB =∠DEC ，再利用AB =DC =2，即可得出∠ABD ∠∠DCE ．(1)在∠ABD 中，∠B +∠BAD +∠ADB =180°，设∠BAD =x °，∠BDA =y °，∠40°+x +y =180°，∠y =140-x （0＜x ＜100），当点D 从点B 向C 运动时，x 增大，∠y 减小，BDA ∠+EDC ∠=180°-140ADE ∠=︒故答案为：小，140；(2)当DC =2时，∠ABD ∠∠DCE ，理由：∠∠C =40°，∠∠DEC +∠EDC =140°，又∠∠ADE =40°，∠∠ADB +∠EDC =140°，∠∠ADB =∠DEC ，又∠AB =DC =2，在∠ABD 和∠DCE 中===ADB DEC B CAB DC ∠∠⎧⎪∠∠⎨⎪⎩， ∠∠ABD ∠∠DCE （AAS ）；【点睛】此题主要考查学生对等腰三角形的判定与性质，全等三角形的判定与性质，三角形外角的性质等知识点的理解和掌握，三角形的内角和公式，解本题的关键是分类讨论．【变式训练】1．（2022·全国·八年级）如图，在∠ABC 中，点D 是边BC 上一点，CD ＝AB ，点E 在边AC 上，且AD ＝DE ，∠BAD ＝∠CDE ．(1)如图1，求证：BD ＝CE ；(2)如图2，若DE 平分∠ADC ，在不添加辅助线的情况下，请直接写出图中所有与∠ADE 相等的角（∠ADE 除外）．【答案】(1)见解析(2)∠EDC ，∠BAD ，∠B ，∠C【解析】【分析】（1）由“SAS ”可证△ABD ∠∠DCE ，可得BD =CE ；（2）由全等三角形的性质可得∠B =∠C ，由三角形的外角性质和角平分线的性质可求解．(1)证明：在∠ABD 和∠DCE 中，AB CD BAD CDE AD DE =⎧⎪∠=∠⎨⎪=⎩，∠∠ABD ∠∠DCE （SAS ），∠BD ＝CE．(2)解：∠∠ABD ∠∠DCE ，∠∠B ＝∠C ，∠DE 平分∠ADC ，∠∠ADE ＝∠CDE ＝∠BAD ，∠∠ADC ＝∠B +∠BAD ＝∠ADE +∠CDE ，∠∠B ＝∠ADE ＝∠BAD ＝∠EDC ＝∠C ，∠与∠ADE 相等的角有∠EDC ，∠BAD ，∠B ，∠C ．【点睛】本题考查了全等三角形的判定和性质，三角形的外角性质，角平分线的定义，掌握全等三角形的判定，明确角度的数量关系是解题的关键．2．（2021·全国·八年级专题练习）如图1，ABC 中，A ABC CB =∠∠．点D 、E 、F 分别是AB 、BC 、AC 边上的点，BE CF =．（1）若DEF ABC ∠=∠，求证：DE EF =；（2）若2180A DEF ∠+∠=︒，9BC =，2EC BE =，求BD 的长：（3）把（1）中的条件和结论反过来，即：若DE EF =，则DEF ABC ∠=∠；这个命题是否成立?若成立，请证明：若不成立，请说明理由．【答案】（1）见解析；（2）6BD =；（3）成立，见解析【解析】【分析】(1)证明DBE ECF ≌即可；(2)求出6EC =，由已知2180A DEF ∠+∠=︒及三角形内角和定理2180A ABC ∠+∠=︒得到DEF ABC ACB ∠=∠=∠，进而证明DBE ECF ≌，即可得到6BD CE ==；(3)过点E 、F 分别作EM AB ⊥于点M ，FN BC ⊥于点N ，证明MBE NCF △≌△，得到ME FN =，再结合条件DE EF =可以证明Rt Rt DME ENF △≌△，进而得到MDE NEF ∠=∠即可求解．【详解】解：(1)如图1所示：由三角形的外角定理可知：DEC ABC BDE ∠=∠+∠，且DEC DEF CEF ∠=∠+∠，DEF ABC ∠=∠，BDE CEF ∴∠=∠，在DBE ∆和ECF ∆中，DBC ECF BDE CEF BE CF ∠=∠⎧⎪∠=∠⎨⎪=⎩，()DBE ECF AAS ≌∴∆∆，DE EF ∴=；(2)9BC =，2EC BE =，6EC ∴=，在ABC ∆中，由三角形内角和定理可知：180A ABC ACB ∠+∠+∠=︒，且A ABC CB =∠∠．2180A ABC ∴∠+∠=︒又2180A DEF ∠+∠=︒，DEF ABC ACB ∴∠=∠=∠，同(1)可知：DBE ECF ≌，6BD CE ∴==；(3)成立，理由如下：过点E 、F 分别作EM AB ⊥于点M ，FN BC ⊥于点N ，如图2所示：EM AB ⊥，FN BC ⊥，90BME CNF ∴∠=∠=︒，又ABC ACB ∠=∠，在MBE △和NCF △中，MBE CNF BMB CNF BE CF ∠=∠⎧⎪∠=∠⎨⎪=⎩()MBE NCF AAS ∴△≌△．ME FN ∴=，又DE EF =，Rt Rt (HL)DME ENF ∴△≌△，MDE NEF ∴∠=∠，又DEC DEF CEF ∠=∠+∠，DEC MDE ABC ∠=∠+∠．DEF ABC ∴∠=∠．即若DE EF =，则DEF ABC ∠=∠此命题成立．【点睛】本题是三角形综合题，考查了角的和差，全等三角形的判定与性质，三角形的外角与不相邻两个内角的关系，重点掌握全等三角形的判定与性质，难点作辅助线构建全等三角形．3．（2022·全国·八年级）（1）如图①，点B 、C 在∠MAN 的边AM 、AN 上，点E ，F 在∠MAN 内部的射线AD 上，∠1、∠2分别是∠ABE 、∠CAF 的外角．已知AB ＝AC ，∠1＝∠2＝∠BAC ．求证：∠ABE ∠∠CAF ．（2）应用：如图②，在∠ABC 中，AB ＝AC ，AB ＞BC ，点D 在边BC 上，且CD ＝2BD ，点E ，F 在线段AD 上．∠1＝∠2＝∠BAC ，若∠ABC 的面积为15，求∠ABE 与∠CDF 的面积之和．【答案】（1）见解析；（2）10【解析】【分析】（1）利用外角的性质和已知角的关系证明∠BAE ＝∠FCA ，∠ABE ＝∠F AC ，利用ASA 即可证明∠ABE ∠∠CAF ； （2）同（1）证明∠ABE ∠∠CAF ，推出S △ABE ＝S △CAF ，S △ABE +S △CDF ＝S △CAF +S △CDF ＝S △ACD ，根据CD ＝2BD 可知23ACD ABC SS =，计算求解即可． 【详解】解：（1）证明如下：∠∠1＝∠2＝∠BAC ，且∠1＝∠BAE +∠ABE ，∠2＝∠F AC +∠FCA ，∠BAC ＝∠BAE +∠F AC ，∠∠BAE ＝∠FCA ，∠ABE ＝∠F AC ，又∠AB ＝AC ，∠∠ABE ∠∠CAF （ASA ）；（2）∠∠1＝∠2＝∠BAC ，且∠1＝∠BAE +∠ABE ，∠2＝∠F AC +∠FCA ，∠BAC ＝∠BAE +∠F AC ，∠∠BAE ＝∠FCA ，∠ABE ＝∠F AC ，又∠AB ＝AC ，∠∠ABE ∠∠CAF （ASA ）∠S △ABE ＝S △CAF ，∠S △ABE +S △CDF ＝S △CAF +S △CDF ＝S △ACD ，∠CD ＝2BD ，∠ABC 的面积为15，∠S △ACD ＝DC BD DC⋅+S △ACD ＝23S △ABC ＝215103⨯=， ∠S △ABE +S △CDF ＝10．【点睛】本题考查了全等三角形的判定和性质，证明∠ABE ∠∠CAF 并掌握“等高三角形面积比等于底边边长之比”是解题的关键．4．（2022·河南郑州·七年级期末）在直线m 上依次取互不重合的三个点,,D A E ，在直线m 上方有AB AC =，且满足BDA AEC BAC α∠=∠=∠=．(1)如图1，当90α=︒时，猜想线段,,DE BD CE 之间的数量关系是____________；(2)如图2，当0180α<<︒时，问题（1）中结论是否仍然成立？如成立，请你给出证明；若不成立，请说明理由；(3)应用：如图3，在ABC 中，BAC ∠是钝角，AB AC =，,BAD CAE BDA AEC BAC ∠<∠∠=∠=∠，直线m 与CB 的延长线交于点F ，若3BC FB =，ABC 的面积是12，求FBD 与ACE 的面积之和．【答案】(1)DE ＝BD +CE(2)DE ＝BD +CE 仍然成立，理由见解析(3)△FBD 与△ACE 的面积之和为4【解析】【分析】（1）由∠BDA ＝∠BAC ＝∠AEC ＝90°得到∠BAD +∠EAC ＝∠BAD +∠DBA ＝90°，进而得到∠DBA ＝∠EAC ，然后结合AB ＝AC 得证△DBA ≌△EAC ，最后得到DE ＝BD +CE ；（2）由∠BDA ＝∠BAC ＝∠AEC ＝α得到∠BAD +∠EAC ＝∠BAD +∠DBA ＝180°﹣α，进而得到∠DBA ＝∠EAC ，然后结合AB ＝AC 得证△DBA ≌△EAC ，最后得到DE ＝BD +CE ；（3）由∠BAD ＞∠CAE ，∠BDA ＝∠AEC ＝∠BAC ，得出∠CAE ＝∠ABD ，由AAS 证得△ADB ≌△CAE ，得出S △ABD ＝S △CEA ，再由不同底等高的两个三角形的面积之比等于底的比，得出S △ABF 即可得出结果．(1)解：DE ＝BD +CE ，理由如下，∵∠BDA ＝∠BAC ＝∠AEC ＝90°，∴∠BAD +∠EAC ＝∠BAD +∠DBA ＝90°，∴∠DBA ＝∠EAC ，∵AB ＝AC ，∴△DBA ≌△EAC （AAS ），∴AD ＝CE ，BD ＝AE ，∴DE ＝AD +AE ＝BD +CE ，故答案为：DE ＝BD +CE ．(2)DE ＝BD +CE 仍然成立，理由如下，∵∠BDA ＝∠BAC ＝∠AEC ＝α，∴∠BAD +∠EAC ＝∠BAD +∠DBA ＝180°﹣α，∴∠DBA ＝∠EAC ，∵AB ＝AC ，∴△DBA ≌△EAC （AAS ），∴BD ＝AE ，AD ＝CE ，∴DE ＝AD +AE ＝BD +CE ；(3)解：∵∠BAD ＜∠CAE ，∠BDA ＝∠AEC ＝∠BAC ，∴∠CAE ＝∠ABD ，在△ABD 和△CAE 中，ABD CAE BDA CEA AB AC ∠=∠⎧⎪∠=∠⎨⎪=⎩，∴△ABD ≌△CAE （AAS ），∴S △ABD ＝S △CAE ，设△ABC的底边BC上的高为h，则△ABF的底边BF上的高为h，∴S△ABC＝12BC•h＝12，S△ABF＝12BF•h，∵BC＝3BF，∴S△ABF＝4，∵S△ABF＝S△BDF+S△ABD＝S△FBD+S△ACE＝4，∴△FBD与△ACE的面积之和为4．【点睛】本题考查了全等三角形的判定与性质、直角三角形的性质，三角形的面积，解题的关键是熟练掌握全等三角形的判定与性质．模型构建三三垂直模型例题：（2021·福建·武夷山市第二中学八年级期中）如图，在∠ABC中，∠ACB = 90°，AC = BC，BE ∠CE于点E，AD ∠CE于点D．（1）求证：△BCE ∠∠CAD；（2）若AD =12，BE =5，求ED的长．【答案】（1）见解析；（2）ED的长为7．【解析】【分析】（1）根据AAS证明三角形全等即可；（2）根据全等三角形的性质得到AD=CE=12，CD=BE=5，从而求得ED的长．【详解】解：（1）证明：∠BE ∠CE于点E，AD ∠CE于点D，∠∠CEB=∠ADC=90°，∠∠ACD+∠CAD=90°，∠∠ACB = 90°，∠∠ACD+∠BCE=90°，∠∠CAD=∠BCE，又∠AC = BC，∠BCE∠CAD；（2）由（1）知，BCE∠CAD，∠BE=CD，CE=AD，∠AD =12，BE =5，∠CE=12，CD=5，∠ED=CE－CD=12－5=7．【点睛】本题考查了全等三角形的判定与性质，熟练掌握判定及性质定理是解题的关键．【变式训练】1．（2021·天津·八年级期中）在∠BAC中，∠BAC＝90°，AB＝AC，AE是过A的一条直线，BD∠AE于点D，CE∠AE于E．(1)如图（1）所示，若B，C在AE的异侧，易得BD与DE，CE的关系是DE＝；(2)若直线AE绕点A旋转到图（2）位置时，（BD＜CE），其余条件不变，问BD与DE，CE的关系如何？请予以证明；(3)若直线AE绕点A旋转，（BD＞CE），问BD与DE，CE的关系如何？请直接写出结果，不需证明．【答案】(1)BD﹣EC(2)BD＝DE﹣CE．见解析(3)当B，C在AE的同侧时，BD＝DE﹣CE；当B，C在AE的异侧时，BD＝DE+CE．【解析】【分析】（1）通过互余关系可得∠ABD ＝∠CAE ，进而证明∠ABD ∠∠ACE （AAS ），即可求得BD ＝AE ，AD ＝EC ，进而即可求得关系式；（2）方法同（1）证明∠ABD ∠∠CAE （AAS ），进而得出结论；（3）综合（1）（2）结论，分当B ，C 在AE 的同侧或异侧时，写出结论即可．(1)结论：DE ＝BD ﹣EC ．理由：如图1中，∠BD ∠AE ，CE ∠AE ，∠∠ADB ＝∠CEA ＝90°，∠∠ABD +∠BAD ＝90°，又∠∠BAC ＝90°，∠∠EAC +∠BAD ＝90°，∠∠ABD ＝∠CAE ，在∠ABD 与∠ACE 中，ADB CEA ABD CAE AB AC ∠=∠⎧⎪∠=∠⎨⎪=⎩，∠∠BAD ∠∠ACE （AAS ），∠BD ＝AE ，AD ＝EC ，∠BD ＝DE +CE ，即DE ＝BD ﹣EC ．故答案为：BD ﹣EC ；(2)结论：BD ＝DE ﹣CE ．理由：如图2中，∠BD ∠AE ，CE ∠AE ，∠∠ADB ＝∠CEA ＝90°，∠∠ABD +∠BAD ＝90°，又∠∠BAC ＝90°，∠∠EAC +∠BAD ＝90°，∠∠ABD ＝∠CAE ，在∠ABD 与∠CAE 中，ADB CEA ABD CAE AB AC ∠=∠⎧⎪∠=∠⎨⎪=⎩，∠∠ABD∠∠CAE（AAS），∠BD＝AE，AD＝EC，∠BD＝DE﹣CE；(3)归纳：由（1）（2）可知：当B，C在AE的同侧时，BD＝DE﹣CE；当B，C在AE的异侧时，BD＝DE+CE．【点睛】本题考查了全等三角形的性质与判定，掌握全等三角形的性质与判定是解题的关键．2．（2022·广东佛山·七年级阶段练习）在△ABC中，△BAC=90°，AC=AB，直线MN经过点A，且CD∠MN于D，BE∠MN于E．∠+∠=度；(1)当直线MN绕点A旋转到图1的位置时，EAB DAC(2)求证：DE=CD+BE；(3)当直线MN绕点A旋转到图2的位置时，试问DE、CD、BE具有怎样的等量关系？请写出这个等量关系，并加以证明．【答案】(1)90°(2)见解析(3)CD= BE + DE，证明见解析【解析】【分析】∠+∠=90°；（1）由△BAC=90°可直接得到EAB DAC（2）由CD∠MN，BE∠MN，得∠ADC=∠BEA=∠BAC=90°，根据等角的余角相等得到∠DCA=∠EAB，根据AAS 可证△DCA∠∠EAB，所以AD=CE，DC=BE，即可得到DE = EA+AD = DC+BE．（3）同（2）易证△DCA∠∠EAB，得到AD=CE，DC=BE，由图可知AE = AD +DE，所以CD= BE + DE．(1)∠△BAC=90°∠ ∠EAB+∠DAC=180°-∠BAC=180°-90°=90°故答案为：90°．(2)证明：∠ CD∠MN于D，BE∠MN于E∠ ∠ADC=∠BEA=∠BAC=90°∠∠DAC+∠DCA=90°且∠DAC+∠EAB=90°∠ ∠DCA=∠EAB∠在△DCA和△EAB中90 ADC BEA DCA EABAC AB ︒⎧∠=∠=⎪∠=∠⎨⎪=⎩∠△DCA∠∠EAB (AAS)∠ AD=BE且EA=DC由图可知：DE = EA+AD = DC+BE．(3)∠ CD∠MN于D，BE∠MN于E∠ ∠ADC=∠BEA=∠BAC=90°∠ ∠DAC+∠DCA=90°且∠DAC+∠EAB=90°∠ ∠DCA=∠EAB∠在△DCA和△EAB中90 ADC BEA DCA EABAC AB ︒⎧∠=∠=⎪∠=∠⎨⎪=⎩∠△DCA∠∠EAB (AAS)∠ AD=BE且AE=CD由图可知：AE = AD +DE∠ CD= BE + DE．【点睛】本题考查了旋转的性质：旋转前后两图形全等，对应点到旋转中心的距离相等，对应点与旋转中心的连线段所夹的角等于旋转角，也考查了三角形全等的判定与性质．3．（2021·北京·东北师范大学附属中学朝阳学校八年级期中）如图，在∠ABC中，∠ACB＝90°，AC＝BC，直线l经过顶点C，过A、B两点分别作l的垂线AE、BF，E、F为垂足．（1）当直线l不与底边AB相交时，①求证：∠EAC＝∠BCF．②猜想EF、AE、BF的数量关系并证明．（2）将直线l 绕点C 顺时针旋转，使l 与底边AB 交于点D （D 不与AB 点重合），请你探究直线l ，EF 、AE 、BF 之间的关系．（直接写出）【答案】（1）①证明见解析，②EF ＝AE +BF ；证明见解析；（2）AE ＝BF +EF 或BF ＝AE +EF ．【解析】【分析】（1）①根据∠AEC ＝∠BFC ＝90°，利用同角的余角相等证明∠EAC ＝∠FCB 即可；②根据AAS 证△EAC ≌△FCB ，推出CE ＝BF ，AE ＝CF 即可；（2）类比（1）证得对应的两个三角形全等，求出线段之间的关系即可．【详解】（1）证明：①∵AE ⊥EF ，BF ⊥EF ，∠ACB ＝90°，∴∠AEC ＝∠BFC ＝∠ACB ＝90°，∴∠EAC +∠ECA ＝90°，∠ECA +∠FCB ＝90°，∴∠EAC ＝∠FCB ，②EF ＝AE +BF ；证明：在△EAC 和△FCB 中，AEC CFB EAC FCB AC BC ∠=∠⎧⎪∠=∠⎨⎪=⎩，∴△EAC ≌△FCB （AAS ），∴CE ＝BF ，AE ＝CF ，∴EF ＝CE +CF ＝AE +BF ，即EF ＝AE +BF ；（2）①当AD ＞BD 时，如图①，∵∠ACB ＝90°，AE ⊥l 直线，同理可证∠BCF ＝∠CAE （同为∠ACD 的余角），又∵AC ＝BC ，BF ⊥l 直线即∠BFC ＝∠AEC ＝90°，∴△ACE ≌△CBF （AAS ），∴CF＝AE，CE＝BF，∵CF＝CE+EF＝BF+EF，∴AE＝BF+EF；②当AD＜BD时，如图②，∵∠ACB＝90°，BF⊥l直线，同理可证∠CBF＝∠ACE（同为∠BCD的余角），又∵AC＝BC，BE⊥l直线，即∠AEC＝∠BFC＝90°．∴△ACE≌△CBF（AAS），∴CF＝AE，BF＝CE，∵CE＝CF+EF＝AE+EF，∴BF＝AE+EF．【点睛】本题考查了三角形综合题，主要涉及到了全等三角形的判定与性质，解题关键是证明△ACE≌△CBF（AAS），利用全等三角形的性质得出线段之间的关系．模型构建四倍长中线模型例题：（2022·全国·八年级课时练习）在△ABC中，AB=5，BC边上的中线AD=4，则AC的长m的取值范围是_______．【答案】3＜m＜13【解析】【分析】延长AD至E，使DE=AD=4，连接CE，利用SAS证明∠ABD∠∠ECD，可得CE=AB，再根据三角形的三边的关系即可解决问题．【详解】解：如图，延长AD至E，使DE=AD=4，连接CE，∠AD 是BC 边上的中线，∠BD =CD ，在∠ADB 和∠CDE 中，AD ED ADB EDC BD CD =⎧⎪∠=∠⎨⎪=⎩，∠∠ABD ∠∠ECD （SAS ），∠CE =AB ，在∠ACE 中，AE -CE ＜AC ＜AE +CE ，∠CE =AB =5，AE =8，∠8-5＜AC ＜8+5，∠3＜AC ＜13，∠3＜m ＜13．故答案为：3＜m ＜13．【点睛】此题考查了全等三角形的性质与判定，三角形的三边的关系，解题的关键是利用已知条件构造全等三角形，然后利用三角形的三边的关系解决问题．【变式训练】1．（2021·江苏·徐州市第二十六中学八年级阶段练习）如图，AD 是∠ABC 中BC 边上的中线，若AB ＝6，AC ＝8，则AD 的取值范围是________________．【答案】1＜AD ＜7【解析】【分析】延长AD 到E ，使DE =AD ，然后利用“边角边”证明∠ABD 和∠ECD 全等，根据全等三角形对应边相等可得CE =AB ，然后根据三角形任意两边之和大于第三边，两边之差小于第三边求出AE 的取值范围，然后即可得解．【详解】解：如图，延长AD 到E ，使DE =AD ，∠AD 是BC 边上的中线，∠BD =CD ，在∠ABD 和∠ECD 中,BD CD ADB EDC AD ED =⎧⎪∠=∠⎨⎪=⎩，∠∠ABD ∠∠ECD (SAS )，∠CE =AB ，∠AB =6，AC =8，∠8-6<AE <8+6，即2<2AD <14，∠1<AD <7，故答案为：1<AD <7．【点睛】本题考查了三角形的三边关系，全等三角形的判定与性质，遇中点加倍延，作辅助线构造出全等三角形是解题的关键．2．（2022·全国·八年级课时练习）已知：多项式x 2+4x +5可以写成（x ﹣1）2+a （x ﹣1）+b 的形式．(1)求a ，b 的值；(2)△ABC 的两边BC ，AC 的长分别是a ，b ，求第三边AB 上的中线CD 的取值范围．【答案】(1)6a =，10b =(2)2<CD <8【解析】【分析】（1）把()()211x a x b -+-+展开，然后根据多项式x 2+4x +5可以写成（x ﹣1）2+a （x ﹣1）+b 的形式，可得2415a a b -=⎧⎨-+=⎩，即可求解； （2）延长CD 至点H ，使CD =DH ，连接AH ，可得∠CDB ∠∠HAD ，从而得到BC =AH =a =6，再根据三角形的三边关系，即可求解．(1)解：∠()()211x a x b -+-+ 221x x ax a b =-++-+()221x a x a b =+-+-+，根据题意得：x 2+4x +5=（x ﹣1）2+a （x ﹣1）+b∠2415a ab -=⎧⎨-+=⎩，解得：610a b =⎧⎨=⎩； (2)解：如图，延长CD 至点H ，使CD =DH ，连接AH ，∠CD 是AB 边上的中线，∠BD =AD ，在∠CDB 和∠HDA 中，∠CD =DH ，∠CDB =∠ADH ，BD =DA ，∠∠CDB ∠∠HDA （SAS ），∠BC =AH =a =6，在∠ACH 中，AC -AH <CH <AC +AH ，∠10-6<2CD <10+6，∠2<CD <8．【点睛】本题主要考查了全等三角形的判定和性质，整式乘法和二元一次方程组的应用，三角形的三边关系，熟练掌握全等三角形的判定和性质，整式乘法法则，三角形的三边关系是解题的关键．3．（2022·全国·八年级课时练习）某数学兴趣小组在活动时，老师提出了这样一个问题：如图，在ABC 中，AB ＝6，AC ＝8，D 是BC 的中点，求BC 边上的中线AD 的取值范围．小明在组内经过合作交流，得到了如下的解决方法：延长AD 到E ，使DE ＝AD ，请补充完整证明“∠ABD ∠∠ECD ”的推理过程．(1)求证：∠ABD ∠∠ECD证明：延长AD 到点E ，使DE ＝AD在∠ABD 和∠ECD 中∠AD ＝ED （已作）∠ADB ＝∠EDC （ ）CD ＝ （中点定义）∠∠ABD ∠∠ECD （ ）(2)由（1）的结论，根据AD 与AE 之间的关系，探究得出AD 的取值范围是 ；(3)【感悟】解题时，条件中若出现“中点”“中线”等字样，可以考虑延长中线构造全等三角形，把分散的已知条件和所求证的结论集合到同一个三角形中．【问题解决】如下图，ABC 中，90B ∠=︒，2AB =，AD 是ABC 的中线，CE BC ⊥，4CE =，且90ADE ∠=︒，求AE 的长．【答案】(1)对顶角相等；BD ；SAS(2)17AD <<(3)6【解析】【分析】（1）延长AD 到点E ，使DE =AD ，根据SAS 定理证明∠ABD ∠∠ECD ；（2）根据全等三角形的性质、三角形的三边关系计算；（3）延长AD 交EC 的延长线于F ，证明△ABD ∠∠FCD ，∠ADE ∠∠FDE ，根据全等三角形的性质解答．(1)延长AD 到点E ，使DE ＝AD在∠ABD 和∠ECD 中∠AD ＝ED （已作）∠ADB ＝∠EDC （对顶角相等）CD ＝BD （中点定义）∠∠ABD ∠∠ECD （SAS ）故答案为：对顶角相等；BD ；SAS(2)∠∠ABD ∠∠ECD ，AB ＝6，AC ＝8，6CE AB ∴==，8686AE -<<+，1AD 7∴<<，故答案为1AD 7<<；(3)延长AD 交EC 的延长线于F ，AB BC ⊥，EF BC ⊥，ABD FCD ∴∠=∠，在ABD △和FCD 中，ABD FCD BD CDADB FDC ∠=∠⎧⎪=⎨⎪∠=∠⎩， ABD ∴∠FCD ，2CF AB ∴==，AD DF =，又∠∠FDE ＝∠ADE ＝90°ED ＝ED∠∠ADE ∠∠FDEAE EF ∴=，426EF CE CF CE AB =+=+=+=，6AE ∴=．【点睛】本题考查了三角形的三边关系定理和全等三角形的性质和判定，解题关键是熟记全等三角形的判定条件． 4．（2022·辽宁沈阳·七年级期中）【问题情境】如图1，A ，B 两点分别位于一个池塘的两端，小明想用绳子测量A ，B 间的距离，但绳子不够长，一个叔叔帮他出了这样一个主意：先在地上取一个可以直接到达A 点和B 点的点C ，连接AC 并延长到D ，使CD CA =；连接BC 并延长到E ，使CE CB =，连接DE 并测量出它的长度，如果100DE =米，那么AB 间的距离为___________米．【探索应用】如图2，在ABC 中，若5,3AB AC ==，求BC 边上的中线AD 的取值范围．解决此问题可以用如下方法：延长AD 到点E 使DE AD =，再连接BE （或将ACD △绕着点D 逆时针旋转180︒得到EBD △），把,2AB AC AD 、集中在ABE △中，利用三角形三边的关系即可判断，中线AD 的取值范围是___________；【拓展提升】如图3，在ABC 中，90,,,90,∠=︒===︒∠=∠ACB AB AD AC AE BAD CAE CA 的延长线交DE 于点F ，求证：DF EF =．【答案】（1）100米；（2）1＜AD ＜4；（3）见详解【解析】【分析】（1）证明∠ABC ∠∠DEC ，由全等三角形的性质即可得AB ＝DE ；（2）延长AD 到点E 使DE AD =，再连接BE ，由“SAS ”可证∠ADC ∠∠EDB ，可得AC ＝BE ＝3，由三角形三边关系可得1＜AD ＜4；（3）在BC 上截取BG ＝AF ，易证△ABG ≌△ADF ，可得DF ＝AG 和∠DF A ＝∠BGA ，即可求证△ACG ≌△EAF ，可得GE ＝AF ，即可解题．【详解】（1）解：在∠ABC 和∠DEC 中，ACB DCE BC EC ⎪∠=∠⎨⎪=⎩，∠∠ABC ∠∠DEC （SAS ），∠DE ＝AB=100米；故答案为：100米（2）延长AD 到点E 使DE AD =，再连接BE如图所示∠AD ＝DE ，CD ＝BD ，∠ADC ＝∠BDE ，∠∠ADC ∠∠EDB （SAS ）∠AC ＝BE ＝3，∠在∠ABE 中，AB ﹣BE ＜AE ＜AB +BE∠2＜2AD ＜8，∠1＜AD ＜4，故答案为：1＜AD ＜4；（3）证明：在BC 上截取BG ＝AF ，∵∠BAD ＝∠CAE ＝∠ACB ＝90°∴∠BAC +∠ABC ＝∠BAC +∠DAF ＝90°∴∠CBA ＝∠DAF ，在△ABG 和△ADF 中，CBA DAF AF BG ⎪∠=∠⎨⎪=⎩，∴△ABG ≌△ADF ，（SAS ）∴DF ＝AG ，∠DF A ＝∠BGA ，∴∠EF A ＝∠CGA ，∵在△ACG 和△EAF 中，EFA CGA BCA EAF AC AE ∠=∠⎧⎪∠=∠⎨⎪=⎩，∴△ACG ≌△EAF （AAS ）∴EE ＝AG ＝FD ．∠DF EF =【点睛】考查了全等三角形的判定和性质，添加恰当辅助线构造全等三角形是本题的关键．。

答卷时应注意事项１、拿到试卷，要认真仔细的先填好自己的考生信息。

２、拿到试卷不要提笔就写，先大致的浏览一遍，有多少大题，每个大题里有几个小题，有什么题型，哪些容易，哪些难，做到心里有底；３、审题，每个题目都要多读几遍，不仅要读大题，还要读小题，不放过每一个字，遇到暂时弄不懂题意的题目，手指点读，多读几遍题目，就能理解题意了；容易混乱的地方也应该多读几遍，比如从小到大，从左到右这样的题；４、每个题目做完了以后，把自己的手从试卷上完全移开，好好的看看有没有被自己的手臂挡住而遗漏的题；试卷第１页和第２页上下衔接的地方一定要注意，仔细看看有没有遗漏的小题；５、中途遇到真的解决不了的难题，注意安排好时间，先把后面会做的做完，再来重新读题，结合平时课堂上所学的知识，解答难题；一定要镇定，不能因此慌了手脚，影响下面的答题；６、卷面要清洁，字迹要清工整，非常重要；７、做完的试卷要检查，这样可以发现刚才可能留下的错误或是可以检查是否有漏题，检查的时候，用手指点读题目，不要管自己的答案，重新分析题意，所有计算题重新计算，判断题重新判断，填空题重新填空，之后把检查的结果与先前做的结果进行对比分析。

亲爱的小朋友，你们好!经过两个月的学习，你们一定有不小的收获吧，用你的自信和智慧，认真答题，相信你一定会闯关成功。

相信你是最棒的！专题02 全等三角形中的六种模型梳理几何探究类问题一直属于考试压轴题范围，在三角形这一章，压轴题主要考查是证明三角形各种模型，或证明线段数量关系等，接来下我们针对其做出详细分析与梳理。

类型一、倍长中线模型中线倍长法：将中点处的线段延长一倍。

目的：①构造出一组全等三角形；②构造出一组平行线。

将分散的条件集中到一个三角形中去。

例1．某数学兴趣小组在一次活动中进行了探究试验活动，请你来加入．【探究与发现】如图1，延长△ABC的边BC到D，使DC＝BC，过D作DE∥AB交AC延长线于点E，求证：△ABC≌△EDC．【理解与应用】如图2，已知在△ABC中，点E在边BC上且∠CAE＝∠B，点E是CD的中点，若AD平分∠BAE．（1）求证：AC＝BD；（2）若BD＝3，AD＝5，AE＝x，求x的取值范围．【答案】[探究与发现]见解析；[理解与应用]（1）见解析；（2）1＜x＜4【详解】解：[探究与发现]证明：∵DE∥AB，∴∠B=∠D，又∵BC=DC，∠ACB=∠ECD，∴△ABC≌△EDC（ASA）；[理解与应用]（1）证明：如图2中，延长AE到F，使EF=EA，连接DF，∵点E 是CD 的中点，∴ED =EC ，在△DEF 与△CEA 中，EF EA DEF CEA ED EC =ìïÐ=Ðíï=î，∴△DEF ≌△CEA （SAS ），∴AC =FD ，∴∠AFD =∠CAE ，∵∠CAE =∠B ，∴∠AFD =∠B ，∵AD 平分∠BAE ，∴∠BAD =∠FAD ，在△ABD 与△AFD 中，B AFD BAD FAD AD AD Ð=ÐìïÐ=Ðíï=î，∴△ABD ≌△AFD （AAS ），∴BD =FD ，∴AC =BD ；（2）解：由（1）得：AF =2AE =2x ，△ABD ≌△AFD ，∴AB =AF =2x ，∵BD =3，AD =5，在△ABD 中，由三角形的三边关系得：AD -BD ＜AB ＜AD +BD ，即5-3＜2x ＜5+3，解得：1＜x ＜4，即x 的取值范围是1＜x ＜4．【变式训练1】如图1，在ABC V 中，CM 是AB 边的中线，BCN BCM Ð=Ð交AB 延长线于点N ，2CM CN =．（1）求证AC BN =；（2）如图2，NP 平分ANC Ð交CM 于点P ，交BC 于点O ，若120AMC Ð=°，CP kAC =，求CP CM的值．【答案】（1）见解析；（2）21kk +【详解】（1）如图1所示，延长CM 至点D ，使CM DM =，在ACM △与BDM V 中，CM DM AMC BMD AM BM =ìïÐ=Ðíï=î，ACM BDM \D @D ，AC BD \=，2CM CN =Q ，CD CN \=，在DCB V 与NCB △中，CD CN DCB NCB CB CB =ìïÐ=Ðíï=î,DCB NCB \D @D ，BN BD \=，AC BN \=；（2）如图所示，120AMC Ð=°Q ，60CMN \Ð=°，NP Q 平分MNC Ð，BCN BCM Ð=Ð，1602PNC BCN AMC Ð+Ð=Ð=°，120CON \Ð=°，60COP Ð=°，180CMN BOP \Ð+Ð=°，作CQ CP =，在CPO △与CQO V 中，CQ CP QCO PCO CO CO =ìïÐ=Ðíï=î，CPO CQO \D @D ，123\Ð=Ð=Ð，45\Ð=Ð，在NOB V 与NOQ V 中，45BNO QNO NO NO Ð=ÐìïÐ=Ðíï=î，NOB NOQ \D @D ，BN NQ \=，CN CP NB \=+，2CM CP AC \=+，设AC a =，CP ka \=，(1)2a k CM +=，21CP k CM k \=+．【变式训练2】（1）如图1，已知ABC V 中，AD 是中线，求证：2AB AC AD +>；（2）如图2，在ABC V 中，D ，E 是BC 的三等分点，求证：AB AC AD AE +>+；（3）如图3，在ABC V 中，D ，E 在边BC 上，且BD CE =．求证：AB AC AD AE +>+．【答案】（1）见解析；（2）见解析；（3）见解析【详解】证：（1）如图所示，延长AD 至P 点，使得AD =PD ，连接CP ，∵AD 是△ABC 的中线，∴D 为BC 的中点，BD =CD ，在△ABD 与△PCD 中，BD CD ADB PDC AD PD =ìïÐ=Ðíï=î，∴△ABD ≌△PCD (SAS )，∴AB =CP ，在△APC 中，由三边关系可得AC +PC ＞AP ，∴2AB AC AD +>；（2）如图所示，取DE 中点H ，连接AH 并延长至Q 点，使得AH =QH ，连接QE 和QC ，∵H 为DE 中点，D 、E 为BC 三等分点，∴DH =EH ，BD =DE =CE ，∴DH =CH，在△ABH 和△QCH 中，BH CH BHA CHQ AH QH =ìïÐ=Ðíï=î，∴△ABH ≌△QCH (SAS )，同理可得：△ADH ≌△QEH ，∴AB =CQ ，AD =EQ ，此时，延长AE ，交CQ 于K 点，∵AC +CQ =AC +CK +QK ，AC +CK ＞AK ，∴AC +CQ ＞AK +QK ，又∵AK +QK =AE +EK +QK ，EK +QK ＞QE ，∴AK +QK ＞AE +QE ，∴AC +CQ ＞AK +QK ＞AE +QE ，∵AB =CQ ，AD =EQ ，∴AB AC AD AE +>+；（3）如图所示，取DE 中点M ，连接AM 并延长至N 点，使得AM =NM ，连接NE ，CE ，∵M 为DE 中点，∴DM =EM ，∵BD =CE ，∴BM =CM ，在△ABM 和△NCM 中，BM CM BMA CMN AM NM =ìïÐ=Ðíï=î，∴△ABM ≌△NCM (SAS )，同理可证△ADM ≌△NEM ，∴AB =NC ，AD =NE ，此时，延长AE ，交CN 于T 点，∵AC +CN =AC +CT +NT ，AC +CT ＞AT ，∴AC +CN ＞AT +NT ，又∵AT +NT =AE +ET +NT ，ET +NT ＞NE ，∴AT +NT ＞AE +NE ，∴AC +CN ＞AT +NT ＞AE +NE ，∵AB =NC ，AD =NE ，∴AB AC AD AE +>+．【变式训练3】在ABC V 中，点P 为BC 边中点，直线a 绕顶点A 旋转，BM ^直线a 于点M ．CN ^直线a 于点N ，连接PM ，PN ．（1）如图1，若点B ，P 在直线a 的异侧，延长MP 交CN 于点E ．求证：PM PE =．（2）若直线a 绕点A 旋转到图2的位置时，点B ，P 在直线a 的同侧，其它条件不变，此时7BMP CNP S S +=△△，1BM =，3CN =，求MN 的长度．（3）若过P 点作PG ^直线a 于点G ．试探究线段PG 、BM 和CN 的关系．【答案】（1）见解析；（2）7MN =；（3）线段PG 、BM 和CN 的位置关系为////BM PG CN ，数量关系为2PG CN BM =-或2PG BM CN =-或2PG CN BM=+【详解】（1）证明：如图1，BM ^Q 直线a 于点M ，CN ^直线a 于点N ，90BMA CNM \Ð=Ð=°，//BM CN \，MBP ECP \Ð=Ð，又P Q 为BC 边中点，BP CP \=，在BPM △和CPE △中，BPM CPE BP CP MBP ECP Ð=Ðìï=íïÐ=Ðî，()BPM CPE ASA \≌△△，PM PE \=．（2）解：如图2，延长MP 与NC 的延长线相交于点E ，BM ^Q 直线a 于点M ，CN ^直线a 于点N ，90BMN CNM \Ð=Ð=°，180BMN CNM \Ð+Ð=°，//BM CN \，MBP ECP \Ð=Ð，又P Q 为BC 中点，BP CP \=，又BPM CPE Ð=ÐQ ，∴在BPM △和CPE △中，BPM CPE BP CP MBP ECP Ð=Ðìï=íïÐ=Ðî，()BPM CPE ASA \≌△△，PM PE \=，BM CE =，BPM CPE S S =△△，∵1BM =，3CN =，4NE CN CE CN BM \=+=+=，7BMP CNP S S +=Q △△，7PNE CPE CNP BMP CNP S S S S S \+=+==△△△△△，214MNE PNE S S \==△△，\14142MN ´´=，7MN \=．（3）位置关系：////BM PG CN ，数量关系：分四种情况讨论∵BM ^直线a 于点M ．CN ^直线a 于点N ，PG ^直线a 于点G ，∴////BM PG CN ，①如图3，当直线a 与线段BP 交于一点时，由（1）可知PM PE =，12PMN PEN MNE S S S \==△△△，即111222MN PG NE MN ´×=×，2NE PG \=，BPM CPE Q ≌△△，BM CE \=，∵NE CN CE =-，2PG CN BM \=-．②当直线a 与线段CP 交于一点时，如图，延长MP 交CN 的延长线于点E ．BM ^Q 直线a 于点M ，CN ^直线a 于点N ，90BMN CNM \Ð=Ð=°，//BM CN \，MBP ECP \Ð=Ð，又P Q 为BC 边中点，BP CP \=，在BPM △和CPE △中，BPM CPE BP CP MBP ECP Ð=Ðìï=íïÐ=Ðî，()BPM CPE ASA \≌△△，PM PE \=．12PMN PEN MNE S S S \==△△△，即111222MN PG NE MN ´×=×，2NE PG \=，BPM CPE Q ≌△△，BM CE \=，∵NE CE CN =-，2PG BM CN \=-．③如图4，当直线a 与线段CB 的延长线交于一点时．由（2）得：()BPM CPE ASA V V ≌，PM PE \=，BPM CPE S S =△△，∴2MNE MNP BCNM S S S ==梯形△△，即()11222BM CN MN MN PG +×=´×，2PG CN BM \=+．④当直线a 与线段CB 的延长线交于一点时，如图，延长MP 交NC 的延长线于点E．BM ^Q 直线a 于点M ，CN ^直线a 于点N ，90BMN CNM \Ð=Ð=°，180BMN CNM \Ð+Ð=°，//BM CN \，MBP ECP \Ð=Ð，又P Q 为BC 中点，BP CP \=，又BPM CPE Ð=ÐQ ，∴在BPM △和CPE △中，BPM CPE BP CP MBP ECP Ð=Ðìï=íïÐ=Ðî，()BPM CPE ASA \≌△△，PM PE \=，BPM CPE S S =△△，∴2MNE MNP BCNM S S S ==梯形△△，即()11222BM CN MN MN PG +×=´×，2PG CN BM \=+．综上所述，线段PG 、BM 和CN 的位置关系为////BM PG CN ，数量关系为2PG CN BM =-或2PG BM CN =-或2PG CN BM =+．类型二、截长补短模型截长补短法使用范围：线段和差的证明（往往需证2次全等）例．在等边三角形ABC 的两边AB 、AC 所在直线上分别有两点M 、N ，P 为△ABC 外一点，且∠MPN ＝60°，∠BPC ＝120°，BP ＝CP ．探究：当点M 、N 分别在直线AB 、AC 上移动时，BM ，NC ，MN 之间的数量关系．(1)如图①，当点M、N在边AB、AC上，且PM＝PN时，试说明MN＝BM+CN．(2)如图②，当点M、N在边AB、AC上，且PM≠PN时，MN＝BM+CN还成立吗？答： ．（请在空格内填“一定成立”“不一定成立”或“一定不成立”）．(3)如图③，当点M、N分别在边AB、CA的延长线上时，请直接写出BM，NC，MN之间的数量关系．【答案】(1)见解析；(2)一定成立；(3)MN＝NC﹣BM【解析】(1)证明：∵△ABC为等边三角形，∴∠ABC＝∠ACB＝60°，∵∠BPC＝120°，BP＝CP，∴∠PBC＝∠PCB＝12×（180°﹣120°）＝30°，∴∠PBM＝∠PCN＝90°，在Rt△PBM和Rt△PCN中，PB PCPM PN=ìí=î，∴Rt△PBM≌Rt△PCN（HL），∴∠BPM＝∠CPN＝30°，∵∠MPN＝60°，PM＝PN，∴△PMN为等边三角形，∴PM＝PN＝MN，在Rt△PBM中，∠BPM＝30°，∴BM＝12PM，同理可得，CN＝12PN，∴BM+CN＝MN．(2)解：一定成立，理由如下：延长AC至H，使CH＝BM，连接PH，如图所示，由（1）可知：∠PBM＝∠PCN＝90°，∴∠PCH＝90°，∴∠PBM＝∠PCH，在△PBM和△PCH中，BM CHPBM PCHPB PC=ìïÐ=Ðíï=î，∴△PBM≌△PCH（SAS），∴PM＝PH，∠BPM＝∠CPH，∵∠BPM +∠CPN ＝60°，∴∠CPN +∠CPH ＝60°，∴∠MPN ＝∠HPN ，在△MPN 和△HPN 中，PM PH MPN HPN PN PN =ìïÐ=Ðíï=î，∴△MPN ≌△HPN （SAS ），∴MN ＝HN ＝BM +CN ，故答案为：一定成立．(3)解：在AC 上截取CK ＝BM ，连接PK ，如图所示，在△PBM 和△PCK 中，90PB PC PBM PCK BM CK =ìïÐ=Ð=°íï=î，∴△PBM ≌△PCK （SAS ），∴PM ＝PK ，∠BPM ＝∠CPK ，∵∠BPM +∠BPN ＝60°，∴∠CPK +∠BPN ＝60°，∴∠KPN ＝60°，∴∠MPN ＝∠KPN ，在△MPN 和△KPN 中，PM PK MPN KPN PN PN =ìïÐ=Ðíï=î，∴△MPN ≌△KPN （SAS ），∴MN ＝KN ，∵KN ＝NC ﹣CK ＝NC ﹣BM ，∴MN ＝NC ﹣BM ．【变式训练1】如图，在四边形ABCD 中，,180AB AD B ADC =Ð+Ð=°，点E 、F 分别在直线BC 、CD 上，且12EAF BAD Ð=Ð．(1)当点E 、F 分别在边BC 、CD 上时（如图1），请说明EF BE FD =+的理由．(2)当点E 、F 分别在边BC 、CD 延长线上时（如图2），（1）中的结论是否仍然成立？若成立，请说明理由；若不成立，请写出EF 、BE 、FD 之间的数量关系，并说明理由．【答案】(1)见解析；(2)不成立，EF BE FD =-，见解析【解析】(1)EF ＝BE +DF ，理由：延长EB 至G ，使BG ＝DF ，连接AG ，∵∠ABC +∠ADC ＝180°，∠ABC +∠ABG ＝180°，∴∠ADC ＝∠ABG ，在△ABG 和△ADF 中，AB AD ABG ADF BG DF =ìïÐ=Ðíï=î，∴△ABG ≌△ADF （SAS ），∴AG ＝AF ，∠BAG ＝∠DAF ，∵∠EAF ＝12∠BAD ，∴∠BAE +∠DAF ＝∠BAE +∠BAG ＝∠EAF ，即∠EAG ＝∠EAF ，在△EAG 和△EAF 中，AG AF EAG EAF AE AE =ìïÐ=Ðíï=î，∴△EAG ≌△EAF （SAS ），∴GE ＝EF ，∴EF ＝BE +DF ；(2)（1）中结论不成立，EF ＝BE ﹣FD ，在BE 上截取BM ＝DF ，连接AM ，∵∠ABC +∠ADC ＝180°，∠ADC +∠ADF ＝180°，∴∠ABC ＝∠ADF ，在△ABM 和△ADF 中，AB AD ABM ADF BM DF =ìïÐ=Ðíï=î，∴△ABM ≌△ADF （SAS ），∴AM ＝AF ，∠BAM ＝∠DAF ，∵∠BAM +∠MAD ＝∠DAF +∠MAD ，∴∠BAD ＝∠MAF，∵∠EAF ＝12∠BAD ，∴∠EAF ＝12∠MAF ，∴∠EAF ＝∠EAM ，在△AME 和△AFE 中，AM AF EAM EAF AE AE =ìïÐ=Ðíï=î，∴△AME ≌△AFE （SAS ），∴ME ＝EF ，∴ME ＝BE ﹣BM ＝BE ﹣DF ，∴EF ＝BE ﹣FD ．【变式训练2】（1）阅读理解：问题：如图1，在四边形ABCD 中，对角线BD 平分ABC Ð，180A C Ð+Ð=°．求证：DA DC =．思考：“角平分线+对角互补”可以通过“截长、补短”等构造全等去解决问题．方法1：在BC 上截取BM BA =，连接DM ，得到全等三角形，进而解决问题；方法2：延长BA 到点N ，使得BN BC =，连接DN ，得到全等三角形，进而解决问题．结合图1，在方法1和方法2中任选一种，添加辅助线并完成证明．（2）问题解决：如图2，在（1）的条件下，连接AC ，当60DAC Ð=°时，探究线段AB ，BC ，BD 之间的数量关系，并说明理由；（3）问题拓展：如图3，在四边形ABCD 中，180A C Ð+Ð=°，DA DC =，过点D 作DE BC ^，垂足为点E ，请直接写出线段AB 、CE 、BC 之间的数量关系．【答案】（1）证明见解析；（2）AB BC BD +=；理由见解析；（3）2BC AB CE -=．【详解】解：（1）方法1：在BC 上截BM BA =，连接DM ，如图．BD Q 平分ABC Ð，ABD CBD \Ð=Ð．在ΔABD 和ΔMBD 中，BD BD ABD MBD BA BM =ìïÐ=Ðíï=î，ΔΔABD MBD \≌，A BMD \Ð=Ð，AD MD =．180BMD CMD °Ð+Ð=Q ，180C A °Ð+Ð=．C CMD \Ð=Ð．DM DC \=，DA DC \=．方法2：延长BA 到点N ，使得BN BC =，连接DN ，如图．BD Q 平分ABC Ð，NBD CBD \Ð=Ð．在ΔNBD 和ΔCBD 中，BD BD NBD CBD BN BC =ìïÐ=Ðíï=î，ΔΔNBD CBD \≌．BND C \Ð=Ð，ND CD =．180NAD BAD °Ð+Ð=Q ，180C BAD °Ð+Ð=．BND NAD \Ð=Ð，DN DA \=，DA DC \=．（2）AB 、BC 、BD 之间的数量关系为：AB BC BD +=．（或者：BD CB AB -=，BD AB CB -=）．延长CB 到点P ，使BP BA =，连接AP ，如图2所示．由（1）可知AD CD =，60DAC °Ð=Q ．ΔADC \为等边三角形．AC AD \=，60ADC °Ð=．180BCD BAD °Ð+Ð=Q ，36018060120ABC °°°°\Ð=--=．18060PBA ABC °°\Ð=-Ð=．BP BA =Q ，ΔABP \为等边三角形．60PAB °\Ð=，AB AP =．60DAC °Ð=Q ，PAB BAC DAC BAC \Ð+Ð=Ð+Ð，即PAC BAD Ð=Ð．在ΔPAC 和ΔBAD 中，PA BA PAC BAD AC AD =ìïÐ=Ðíï=î，ΔΔPAC BAD \≌．PC BD \=，PC BP BC AB BC =+=+Q ，AB BC BD \+=．（3）AB ，CE ，BC 之间的数量关系为：2BC AB CE -=．（或者：2BC CE AB -=，2AB CE BC +=）解：连接BD ，过点D 作DF AC ^于F ，如图3所示．180BAD C °Ð+Ð=Q ，180BAD FAD °Ð+Ð=．FAD C \Ð=Ð．在ΔDFA 和ΔDEC 中，DFA DEC FAD C DA DC Ð=ÐìïÐ=Ðíï=î，ΔΔDFA DEC \≌，DF DE \=，AF CE =．在RtΔBDF 和RtΔBDE 中，BD BD DF DE =ìí=î，RtΔRtΔBDF BDE \≌．BF BE \=，2BC BE CE BA AF CE BA CE \=+=++=+，2BC BA CE \-=．【变式训练3】在ABC V 中，BE ，CD 为ABC V 的角平分线，BE ，CD 交于点F ．（1）求证：1902BFC A Ð=°+Ð；（2）已知60A Ð=°．①如图1，若4BD =， 6.5BC =，求CE 的长；②如图2，若BF AC =，求AEB Ð的大小．【答案】（1）证明见解析；（2）2.5；（3）100°．【解析】解：（1）BE Q 、CD 分别是ABC Ð与ACB Ð的角平分线，11(180)9022FBC FCB A A \Ð+Ð=°-Ð=°-Ð，1180()180(90)2BFC FBC FCB A \Ð=°-Ð+Ð=°-°-Ð，1902BFC A \Ð=°+Ð，（2）如解（2）图，在BC 上取一点G 使BG=BD ，由（1）得1902BFC A Ð=°+Ð，60BAC Ð=°Q ，120BFC \Ð=°，∴18060BFD EFC BFC Ð=Ð=°-Ð=°，在BFG V 与BFD △中，BF BF FBG FBD BD BG =ìïÐ=Ðíï=î，∴BFG BFD @V △（SAS ）∴BFD BFG Ð=Ð，∴60BFD BFG Ð=Ð=°，∴12060CFG BFG Ð=°-Ð=°，∴60CFG CFE Ð=Ð=°在FEC V 与FGC △中，CFE CFG CF CF ECF GCF Ð=Ðìï=íïÐ=Ðî，()FEC FGC ASA \@V V ，CE CG \=，BC BG CG =+Q ，BC BD CE \=+；∵4BD =， 6.5BC =，∴ 2.5CE =（3）如解（3）图，延长BA 到P ，使AP=FC，60BAC Ð=°Q ，∴180120PAC BAC Ð=°-Ð=°，在BFC △与CAP V 中，120BF AC BFC CAP CF PA =ìïÐ=Ð=°íï=î，∴BFC CAP @V △（SAS ）∴P BCF Ð=Ð，BC PC =，∴P ABC Ð=Ð，又∵12P BCF ACB Ð=Ð=Ð，∴2ACB ABC Ð=Ð，又∵180ACB ABC A Ð+Ð+Ð=°，∴360180ABC Ð+°=°，∴40ABC Ð=°，80ACB Ð=°，∴1202ABE ABC Ð=Ð=°，180()180(2060)100AEB ABE A Ð=°-Ð+Ð=°-°+°=°类型三、做平行线证明全等例1．如图所示：ABC V 是等边三角形，D 、E 分别是AB 及AC 延长线上的一点，且BD CE =，连接DE 交BC 于点M ．求让：MD ME=【答案】见详解【详解】过点D 作DE ∥AC ，交BC 于点E ，∵ABC V 是等边三角形，∴∠B=∠ACB=60°，∵DE ∥AC ，∴∠DEB=∠ACB=60°，∠MDE=∠MEC ，∴BDE V 是等边三角形，∴BD=DE ，∵BD CE =，∴DE=CE ，又∵∠EMD=∠CME ，∴∆EMD ≅∆CME ，∴MD ME =．【变式训练1】 P 为等边△ABC 的边AB 上一点，Q 为BC 延长线上一点，且PA ＝CQ ，连PQ 交AC 边于D ．（1）证明：PD ＝DQ ．（2）如图2，过P 作PE ⊥AC 于E ，若AB ＝6，求DE 的长．【答案】（1）证明见解析；（2）DE ＝3．【详解】（1）如图1所示，点P 作PF ∥BC 交AC 于点F ．∵△ABC 是等边三角形，∴△APF 也是等边三角形，AP =PF =AF =CQ ．∵PF ∥BC ，∴∠PFD =∠DCQ ．在△PDF 和△QDC 中，PDF QDC DFP QCDPF QC Ð=ÐìïÐ=Ðíï=î，∴△PDF ≌△QDC （AAS ），∴PD =DQ ；（2）如图2所示，过P 作PF ∥BC 交AC 于F ．∵PF ∥BC ，△ABC 是等边三角形，∴∠PFD =∠QCD ，△APF 是等边三角形，∴AP =PF =AF ．∵PE ⊥AC ，∴AE =EF ．∵AP =PF ，AP =CQ ，∴PF =CQ ．在△PFD 和△QCD 中，PDF QDC DFP QCDPF QC Ð=ÐìïÐ=Ðíï=î，∴△PFD ≌△QCD （AAS ），∴FD =CD ．∵AE =EF ，∴EF +FD =AE +CD ，∴AE +CD =DE 12=AC ．∵AC =6，∴DE =3．【变式训练2】已知在等腰△ABC中，AB=AC，在射线CA上截取线段CE，在射线AB上截取线段BD，连接DE，DE所在直线交直线BC与点M．请探究：(1)如图（1），当点E在线段AC上，点D在AB延长线上时，若BD=CE，请判断线段MD和线段ME的数量关系，并证明你的结论．(2)如图（2），当点E在CA的延长线上，点D在AB的延长线上时，若BD=CE，则（1）中的结论还成立吗？如果成立，请证明；如果不成立，说明理由；ME．【答案】(1)DM=EM．理由见详解；(2)成立，理由见详解；(3)MD=12【解析】(1)解：DM=EM；证明：过点E作EF//AB交BC于点F，∵AB=AC，∴∠ABC=∠C；又∵EF//AB，∴∠ABC=∠EFC，∴∠EFC=∠C，∴EF=EC．又∵BD=EC，∴EF=BD．又∵EF//AB，∴∠ADM=∠MEF．在△DBM 和△EFM 中BDM FEM BMD FME BD EF Ð=ÐìïÐ=Ðíï=î，∴△DBM ≌△EFM ，∴DM =EM ．(2)解：成立；证明：过点E 作EF //AB 交CB 的延长线于点F ，∵AB =AC ，∴∠ABC =∠C ；又∵EF //AB ，∴∠ABC =∠EFC ，∴∠EFC =∠C ，∴EF =EC ．又∵BD =EC ，∴EF =BD ．又∵EF //AB ，∴∠ADM =∠MEF ．在△DBM 和△EFM 中BDE FEM BMD FME BD EF Ð=ÐìïÐ=Ðíï=î∴△DBM ≌△EFM ；∴DM =EM ；类型四、旋转模型例．如图1，AC BC =，CD CE =，ACB DCE a Ð=Ð=，AD 、BE 相交于点M ，连接CM ．（1）求证：BE AD =，并用含a 的式子表示AMB Ð的度数；（2）当90a =°时，取AD ，BE 的中点分别为点P 、Q ，连接CP ，CQ ，PQ ，如图2，判断CPQ V 的形状，并加以证明．【答案】（1）证明见解析；AMB a Ð=；（2）CPQ V 为等腰直角三角形；证明见解析．【详解】证明：（1）如图1，ACB DCE a Ð=Ð=Q ，ACB BCD DCE BCD \Ð+Ð=Ð+Ð，ACD BCE ÐÐ\=，在ACD △和BCE V 中，CA CB ACD BCE CD CE =ìïÐ=Ðíï=î，(SAS)ACD BCE \≌△△，BE AD \=；ACD BCE V Q V ≌，CAD CBE \Ð=Ð，ABC Q V 中，180BAC ABC a Ð+Ð=°-，180BAM CAM ABC a \Ð+Ð+Ð=°-,180BAM ABM a \Ð+Ð=°-，ABM \V 中，180()180(180)AMB BAM ABM a a Ð=°-Ð+Ð=°-°-=；即AMB a Ð=；（2）CPQ V 为等腰直角三角形．证明：如图2，由（1）可得，BE AD =，AD Q ，BE 的中点分别为点P 、Q ，AP =BQ \，ACD BCE V Q V ≌，CAP CBQ \Ð=Ð，在ACP △和BCQ △中，CA CB CAP CBQ AP BQ =ìïÐ=Ðíï=î，(SAS)ACP BCQ \≌△△，CP CQ \=，且ACP BCQ Ð=Ð，又90ACP PCB Ð+Ð=°Q ，90BCQ PCB \Ð+Ð=°，90PCQ \Ð=°，CPQ \V 为等腰直角三角形．【变式训练1】四边形ABCD 是由等边ABC D 和顶角为120°的等腰ABD D 排成，将一个60°角顶点放在D 处，将60°角绕D 点旋转，该60°交两边分别交直线BC 、AC 于M 、N ，交直线AB 于E 、F 两点．（1）当E 、F 都在线段AB 上时（如图1），请证明：BM AN MN +=；（2）当点E 在边BA 的延长线上时（如图2），请你写出线段MB ，AN 和MN 之间的数量关系，并证明你的结论；（3）在（1）的条件下，若7AC =， 2.1AE =，请直接写出MB 的长为 ．【答案】（1）证明见解析；（2）MB MN AN =+．证明见解析；（3）2.8．【解析】解：（1）证明：把△DBM 绕点D 逆时针旋转120°得到△DAQ ，则DM =DQ ，AQ =BM ，∠ADQ =∠BDM ，∠QAD =∠CBD =90°，∴点Q 在直线CA 上，∵∠QDN =∠ADQ +∠ADN =∠BDM +∠ADN =∠ABD -∠MDN =120°-60°=60°，∴∠QDN =∠MDN =60°，∵在△MND 和△QND 中，DM DQ QDN MDN DN DN ìïÐÐíïî＝＝＝，∴△MND ≌△QND （SAS ），∴MN =QN ，∵QN =AQ +AN =BM +AN ，∴BM +AN =MN ；（2）：MB MN AN =+.理由如下：如图，把△DAN 绕点D 顺时针旋转120°得到△DBP ，则DN =DP ，AN =BP ，∵∠DAN =∠DBP =90°，∴点P 在BM 上，∵∠MDP =∠ADB -∠ADM -∠BDP =120°-∠ADM -∠ADN =120°-∠MDN =120°-60°=60°，∴∠MDP =∠MDN =60°，∵在△MND 和△MPD 中，DN DP MDP MDN DM DM ìïÐÐíïî＝＝＝，∴△MND ≌△MPD （SAS ），∴MN =MP ，∵BM =MP +BP ，∴MN +AN =BM；（3）如图，过点M作MH∥AC交AB于G，交DN于H，∵△ABC是等边三角形，∴△BMG是等边三角形，∴BM=MG=BG，根据（1）△MND≌△QND可得∠QND=∠MND，根据MH∥AC可得∠QND=∠MHN，∴∠MND=∠MHN，∴MN=MH，∴GH=MH-MG=MN-BM=AN，即AN=GH，∵在△ANE和△GHE中，QND MHNAEN GEHAN GHÐÐìïÐÐíïî＝＝＝，∴△ANE≌△GHE（AAS），∴AE=EG=2.1，∵AC=7，∴AB=AC=7，∴BG=AB-AE-EG=7-2.1-2.1=2.8，∴BM=BG=2.8．故答案为：2.8【变式训练2】（1）问题发现：如图1，△ACB和△DCE均为等边三角形，当△DCE旋转至点A，D，E在同一直线上，连接BE．则：①∠AEB的度数为 °；②线段AD、BE之间的数量关系是 ．（2）拓展研究：如图2，△ACB和△DCE均为等腰三角形，且∠ACB＝∠DCE＝90°，点A、D、E在同一直线上，若AD＝a，AE＝b，AB＝c，求a、b、c之间的数量关系．（3）探究发现：图1中的△ACB和△DCE，在△DCE旋转过程中，当点A，D，E不在同一直线上时，设直线AD与BE相交于点O，试在备用图中探索∠AOE的度数，直接写出结果，不必说明理由．【答案】（1）①60；②AD ＝BE ；（2）a 2＋b 2＝c 2；（3）60°或120°【详解】解：（1）①如图1，∵△ACB 和△DCE 均为等边三角形，∴CA =CB ，CD =CE ，∠ACB =∠DCE =60°，∴∠ACD =∠BCE ，在△ACD 和△BCE 中，AC BC ACD BCE CD CE =ìïÐ=Ðíï=î，∴△ACD ≌△BCE （SAS ）．∴∠ADC =∠BEC ．∵△DCE 为等边三角形，∴∠CDE =∠CED =60°，∵点A ，D ，E 在同一直线上，∴∠ADC =120°，∴∠BEC =120°，∴∠AEB =∠BEC -∠CED =60°，故答案为：60；②∵△ACD ≌△BCE ，∴AD =BE ，故答案为：AD =BE ；（2）∵△ACB 和△DCE 均为等腰直角三角形，∴CA =CB ，CD =CE ，∠ACB =∠DCE =90°．∴∠ACD =∠BCE ，∴△ACD ≌△BCE （SAS ），∴BE =AD ，∠ADC =∠BEC ，∵△DCE 为等腰直角三角形，∴∠CDE =∠CED =45°．∵点A ，D ，E 在同一直线上，∴∠ADC =135°．∴∠BEC =135°，∴∠AEB =∠BEC -∠CED =90°，∴AD 2+AE 2=AB 2，∵AD =a ，AE =b ，AB =c ，∴a 2+b 2=c 2；（3）如图3，由（1）知△ACD ≌△BCE ，∴∠CAD =∠CBE ，∵∠CAB =∠CBA =60°，∴∠OAB +∠OBA =120°，∴∠AOE =180°-120°=60°，如图4，同理求得∠AOB =60°，∴∠AOE =120°，∴∠AOE 的度数是60°或120°．【变式训练3】如图1，在Rt ABC V 中，90A Ð=°，AB AC =，点D ，E 分别在边AB ，AC 上，AD AE =，连接DC ，点M ，P ，N 分别为DE ，DC ，BC 的中点．（1）观察猜想：图1中，线段PM 与PN 的数量关系是______，位置关系是______．（2）探究证明：把ADE V 绕点A 逆时针方向旋转到图2的位置，连接MN ，BD ，CE ，判断PMN V 的形状，并说明理由；（3）拓展延伸：把ADE V 绕点A 在平面内自由旋转，若4=AD ，10AB =，请直接写出PMN V 面积的最大值．【答案】（1）PM PN =、PM PN ^；（2）等腰直角三角形，证明见解析；（3）492【详解】解：（1）∵点P ，N 是BC ，CD 的中点， ∴PN ∥BD ，PN =12BD ，∵点P ，M 是CD ，DE 的中点， ∴PM ∥CE ，PM =12CE ，∵AB =AC ，AD =AE ， ∴BD =CE ， ∴PM =PN ，∵PN ∥BD ， ∴∠DPN =∠ADC ，∵PM ∥CE ， ∴∠DPM =∠DCA ，∵∠BAC =90°， ∴∠ADC +∠ACD =90°， ∴∠MPN =∠DPM +∠DPN =∠DCA +∠ADC =90°，∴PM⊥PN，故答案为：PM=PN，PM⊥PN；（2）△PMN是等腰直角三角形．理由如下：由旋转知，∠BAD=∠CAE，∵AB=AC，AD=AE，∴△ABD≌△ACE（SAS），∴∠ABD=∠ACE，BD=CE，利用三角形的中位线得，PN=12BD，PM=12CE，∴PM=PN，∴△PMN是等腰三角形，同（1）的方法得，PM∥CE，∴∠DPM=∠DCE，同（1）的方法得，PN∥BD，∴∠PNC=∠DBC，∵∠DPN=∠DCB+∠PNC=∠DCB+∠DBC，∴∠MPN=∠DPM+∠DPN=∠DCE+∠DCB+∠DBC =∠BCE+∠DBC=∠ACB+∠ACE+∠DBC=∠ACB+∠ABD+∠DBC=∠ACB+∠ABC，∵∠BAC=90°，∴∠ACB+∠ABC=90°，∴∠MPN=90°，∴△PMN是等腰直角三角形；（3）由（2）知，△PMN是等腰直角三角形，PM=PN=12BD，∴PM最大时，△PMN面积最大，∴点D在BA的延长线上，∴BD=AB+AD=14，∴PM=7，∴S△PMN最大= 12PM2=12×49=492．类型五、手拉手模型例．在等边ABCV中，点D在AB上，点E在BC上，将线段DE绕点D逆时针旋转60°得到线段DF，连接CF．(1)如图（1），点D 是AB 的中点，点E 与点C 重合，连接AF ．若6AB =，求AF 的长；(2)如图（2），点G 在AC 上且60AGD FCB Ð=°+Ð，求证：CF DG =；(3)如图（3），6AB =，2BD CE =，连接AF ．过点F 作AF 的垂线交AC 于点P ，连接BP 、DP ．将BDP △沿着BP 翻折得到BQP V ，连接QC ．当ADP △的周长最小时，直接写出CPQ V 的面积．【答案】(1)AF =3；(2)见解析；【解析】(1)解：∵△ABC 为等边三角形，∴BC =AC ，∠BCA =60°，由旋转知，∠CDF =60°，CD =CF ，∴△DCF 为等边三角形，∴CD =CF ，∠DCF =60°，∴∠DCB =∠ACF ，∴△BCD ≌△ACF ，∴AF =BD ，∵D 为AB 中点，AB =6，∴BD =3，∴AF =3．(2)解：将CF 绕C 顺时针旋转60°得CH ，连接CH ，FH ，EF ，EH ，CD ，在AC 上截取AP =BE ，连接DP ，设CD 交EH 于M ，如图所示，由旋转知，△DEF 、△CFH 为等边三角形，∴DF =EF ，CF =FH ，∠DFE =∠CFH =60°，∴∠DFC =∠EFH ，∴△DCF ≌△BHF ，∴EH =CD ，∠DCF =∠EHF ，由三角形内角和知，∠HMC +∠EHF =∠DCF +∠HFC ，∴∠HMC =∠HFC =60°，∴∠DCE +∠HEC =60°，∵∠DCP +∠DCE =60°， ∴∠CEH =∠DCP ，∵AC =BC ，AP =BE ，∴CP =CE ，∴△ECH ≌△CPD ，∴CH =DP ，∠DPC =∠HCE ，又∠HCE =60°+∠2，∴∠DPC =60°+∠2，由∠1+∠FCG =∠2+∠FCG =60°，知∠1=∠2，又∠AGD =60°+∠1，∴∠AGD =∠DPG ， ∴DP =DG ，∵CH =CF ，∴CF =DG ．(3)：过D 作DH ⊥CB 于H ，连接EF ，如图所示，∵△ABC 为等边三角形，∴∠DBH =60°，∠BDH =30°，∴BD =2BH ，DH ，∵BD =2CE ，∴BH =CE ，设BH =CE =x ，则BD =2x ，EH =6－2x ，AD =6－2x ，由旋转知，△DEF 为等边三角形，∠EDF =60°，∴∠1+∠3=90°，DE =DF ，又∠1+∠2=90°，∴∠2=∠3，∴△ADF ≌△HED ，∴∠DAF =∠DHE =90°，∠PAF =30°，AF =DH ，∵∠AFP =90°，∴PF =x ，AP =2x ，过P 作PM ⊥AD 于M ，则AM =x ，DM =6－3x ，PM ，在Rt △PDM 中，由勾股定理得：PD ==故△ADP 周长=AD +AP +PD =6－2x +2x ，∴当x =32时，周长取最小值，最小值为9，此时DP =3，∴BD =AP =3，即D 为AB 中点，P 为AC 中点，∴直线BP 是等边△ABC 对称轴，如图所示，△BDP 沿BP 折叠后，Q 点落在BC 中点处，则△PCQ 面积=14×△ABC 面积=1426【变式训练1】△ACB 和△DCE 是共顶点C 的两个大小不一样的等边三角形．(1)问题发现：如图1，若点A，D，E在同一直线上，连接AE，BE．①求证：△ACD≌△BCE；②求∠AEB的度数．(2)类比探究：如图2，点B、D、E在同一直线上，连接AE，AD，BE，CM为△DCE中DE边上的高，请求∠ADB的度数及线段DB，AD，DM之间的数量关系，并说明理由．(3)拓展延伸：如图3，若设AD（或其延长线）与BE的所夹锐角为α，则你认为α为多少度，并证明．【答案】(1)①见解析；②∠AEB=60°；(2)∠ADB=60°，2DM+BD=AD，理由见解析；(3)α=60°，证明见解析【解析】(1)①证明：∵△ACB和△DCE是等边三角形，∴AC=BC，CD=CE，∠ACB=∠DCE=60°，∴∠ACD=60°-∠DCB=∠BCE，∴△ACD≌△BCE（SAS）；②∵△ACD≌△BCE，∴∠ADC=∠BEC=180°-∠CDE=120°，又∵∠CED=60°，∴∠AEB=60°；(2)解：∠ADB=60°，2DM +BD=AD，理由如下；∵AC=BC，CD=CE，∠ACD=60°+∠DCB=∠BCE，∴△ACD≌△BCE（SAS），∴∠CDA=∠CED=60°；∵∠ADB+∠CDA=∠DCE+∠CED，∴∠ADB=60°；又∵CM⊥BE，且△CDE为等边三角形，∴DE=2DM，∴2DM +BD=BE=AD；(3)解：α=60°，理由如下：同理可证△ACD≌△BCE，∴∠BEC=∠ADC，∴∠CDF+∠CEF=180°，∴∠ECD+∠DFE=180°，而α+∠DFE=180°，∴α=∠ECD=60°．【变式训练2】（1）如图1，锐角△ABC中，分别以AB、AC为边向外作等腰直角△ABE和等腰直角△ACD，使AE＝AB，AD＝AC，∠BAE＝∠CAD＝90°，连接BD，CE，试猜想BD与CE的大小关系，不需要证明．【深入探究】（2）如图2，四边形ABCD中，AB＝5，BC＝2，∠ABC＝∠ACD＝∠ADC＝45°，求BD2的值；甲同学受到第一问的启发构造了如图所示的一个和△ABD全等的三角形，将BD进行转化再计算，请你准确的叙述辅助线的作法，再计算；【变式思考】（3）如图3，四边形ABCD中，AB＝BC，∠ABC＝60°，∠ADC＝30°，AD＝6，BD＝10，则CD＝ ．【答案】（1）BD ＝CE ；（2）BD 2＝54；（3）8【详解】解：（1）BD ＝CE ．理由是：∵∠BAE ＝∠CAD ， ∴∠BAE +∠BAC ＝∠CAD +∠BAC ，即∠EAC ＝∠BAD ，在△EAC 和△BAD 中， AE AB EAC BAD AC AD =ìïÐ=Ðíï=î，∴△EAC ≌△BAD ， ∴BD ＝CE ；（2）如图2，在△ABC 的外部，以A 为直角顶点作等腰直角△BAE ，使∠BAE ＝90°，AE ＝AB ，连接EA 、EB 、EC ．∵∠ACD ＝∠ADC ＝45°， ∴AC ＝AD ，∠CAD ＝90°，∴∠BAE +∠BAC ＝∠CAD +∠BAC ，即∠EAC ＝∠BAD ，在△EAC 和△BAD 中，AE AB EAC BAD AC AD =ìïÐ=Ðíï=î，∴△EAC ≌△BAD ，∴BD ＝CE ．∵AE ＝AB ＝5，∴BE =∠ABE ＝∠AEB ＝45°，又∵∠ABC ＝45°，∴∠ABC +∠ABE ＝45°+45°＝90°，∴(22222254EC BE BC =+=+=，∴2254BD CE == ．（3）如图，∵AB ＝BC ，∠ABC ＝60°，∴△ABC 是等边三角形，把△ACD 绕点C 逆时针旋转60°得到△BCE ，连接DE ，则BE ＝AD ，△CDE 是等边三角形，∴DE ＝CD ，∠CED ＝60°，∵∠ADC ＝30°，∴∠BED ＝30°+60°＝90°，在Rt △BDE 中，DE 8，∴CD ＝DE ＝8．【变式训练3】（1）问题发现：如图1，ACB △和DCE V 均为等腰直角三角形，90ACB DCE Ð=Ð=°，连接AD ，BE ，点A 、D 、E 在同一条直线上，则AEB Ð的度数为__________，线段AD 、BE 之间的数量关系__________；（2）拓展探究：如图2，ACB △和DCE V 均为等腰直角三角形，90ACB DCE Ð=Ð=°，连接AD ，BE ，点A 、D 、E 不在一条直线上，请判断线段AD 、BE 之间的数量关系和位置关系，并说明理由．（3）解决问题：如图3，ACB △和DCE V 均为等腰三角形，ACB DCE a Ð=Ð=，则直线AD 和BE 的夹角为__________．（请用含a 的式子表示）【答案】（1）90°，AD =BE ；（2）AD =BE ，AD ⊥BE ；（3）a【详解】（1）∵ACB △和DCE V 均为等腰直角三角形，90ACB DCE Ð=Ð=°，∴AC BC ＝，CD CE ＝，∠CDE =45°∴∠CDA =135°∵∠ACB −∠DCB ＝∠DCE −∠DCB ，∴∠ACD ＝∠BCE ．在△ACD 和△BCE 中，AC BC ACD BCE CD CE ìïÐÐíïî＝＝＝，∴△ACD ≌△BCE （SAS ），∴∠BEC =∠ADC ＝135°，AD ＝BE ，∴∠AEB =90°故答案为：90°，AD ＝BE（2）AD =BE ，AD ⊥BE ，理由如下，（3）同理可得△ACD ≌△BCE ，则AD =BE ，延长AD 交BE 于点F ，设∠FAB =α，则∠CAD =∠CBE =45°-α∴∠ABE =45°+45°-α=90°-α∴∠AFB =180°-∠FAB -∠ABE =180°-α-(90°-α)=90°∴AD ⊥BE（3）如图，延长BE 交AD 于点G，∵ACB △和DCE V 均为等腰三角形，∴AC BC ＝，CD CE ＝，∵∠ACB =∠DCE =α，∵∠ACB +∠ACE ＝∠DCE +∠ACE ，∴∠ACD ＝∠BCE ．在△ACD 和△BCE 中，AC BC ACD BCE CD CE ìïÐÐíïî＝＝＝，∴△ACD ≌△BCE （SAS ），∴∠CBE =∠CAD ∵ACB DCE a Ð=Ð=，∴∠CBA =∠CAB =()11180=9022a a °-°-∴∠GAB +∠GBA =()()CAD CAB ABC CBE Ð+Ð+Ð-ÐABC CAB =Ð+Ð180a =°-，∴∠AGB =180°-(∠GAB +∠GBA )a = ，即直线AD 和BE 的夹角为a ．故答案为：a ．类型六、一线三角模型例.在ABC V 中，90ACB Ð=°，AC BC =，直线MN 经过点C 且AD MN ^于D ，BE MN ^于E ．(1)当直线MN 绕点C 旋转到图1的位置时，求证：①ADC V ≌CEB △；②DE AD BE =+；(2)当直线MN 烧点C 旋转到图2的位置时，求证：DE AD BE =-；(3)当直线MN 绕点C 旋转到图3的位置时，试问DE 、AD 、BE 具有怎样的等量关系？请写出这个等量关系，并加以证明．【答案】(1)①证明见解析；②证明见解析；(2)证明见解析(3)DE BE AD =-（或者对其恒等变形得到AD BE DE =-，BE AD DE =+），证明见解析【解析】(1)解：①AD MN ^Q ，BE MN ^，90ADC ACB CEB \Ð=Ð=°=Ð，90CAD ACD \Ð+Ð=°，90BCE ACD Ð+Ð=°，CAD BCE \Ð=Ð，Q 在ADC D 和CEB D 中，CAD BCE ADC CEB AC BC Ð=ÐìïÐ=Ðíï=î()ADC CEB AAS \D @D ；②ADC CEB D @D Q ，CE AD \=，CD BE =，DE CE CD AD BE \=+=+；(2)证明：AD MN ^Q ，BE MN ^，90ADC CEB ACB \Ð=Ð=Ð=°，CAD BCE \Ð=Ð，Q 在ADC D 和CEB D 中，CAD BCE ADC CEB AC BC Ð=ÐìïÐ=Ðíï=î()ADC CEB AAS \D @D ；CE AD \=，CD BE =，DE CE CD AD BE \=-=-；(3)证明：当MN 旋转到题图（3）的位置时，AD ，DE ，BE 所满足的等量关系是：DE BE AD =-或AD BE DE =+或BE AD DE =+．理由如下：AD MN ^Q ，BE MN ^，90ADC CEB ACB \Ð=Ð=Ð=°，CAD BCE \Ð=Ð，Q 在ADC D 和CEB D 中，CAD BCE ADC CEBAC BC Ð=ÐìïÐ=Ðíï=î()ADC CEB AAS \D @D ，CE AD \=，CD BE =，DE CD CE BE AD \=-=-（或者对其恒等变形得到AD BE DE =+或BE AD DE =+）．【变式训练1】【问题解决】（1）已知△ABC 中，AB =AC ，D ，A ，E 三点都在直线l 上，且有∠BDA =∠AEC =∠BAC ．如图①，当∠BAC =90°时，线段DE ，BD ，CE 的数量关系为：______________；【类比探究】（2）如图②，在（1）的条件下，当0°<∠BAC <180°时，线段DE ，BD ，CE 的数量关系是否变化，若不变，请证明：若变化，写出它们的关系式；【拓展应用】（3）如图③，AC =BC ，∠ACB =90°，点C 的坐标为（-2，0），点B 的坐标为（1，2），请求出点A 的坐标．【答案】（1）DE ＝BD +CE ；（2）DE ＝BD +CE 的数量关系不变，理由见解析；（3）（﹣4，3）【解析】解：（1）∵∠BAC ＝90°，∴∠BDA ＝∠AEC ＝∠BAC ＝90°，∴∠ABD +∠BAD ＝90°，∠CAE +∠BAD ＝90°，∴∠ABD ＝∠CAE ，在△ABD 和△CAE 中，ABD CAE ADB CEA BA AC Ð=ÐìïÐ=Ðíï=î，∴△ABD ≌△CAE （AAS ），∴AD ＝CE ，BD ＝AE ，∴DE ＝AD +AE ＝BD +CE ，故答案为：DE ＝BD +CE ；（2）DE ＝BD +CE 的数量关系不变，理由如下：∵∠BAE 是△ABD 的一个外角，∴∠BAE ＝∠ADB +∠ABD ，∵∠BDA ＝∠BAC ，∴∠ABD ＝∠CAE ，在△ABD 和△CAE 中，ABD CAE ADB CEA BA AC Ð=ÐìïÐ=Ðíï=î，∴△ABD ≌△CAE （AAS ），∴AD ＝CE ，BD ＝AE ，∴DE ＝AD +AE ＝BD +CE；。

全等三角形基本模型（4大模型）模型一：平移型模型二：翻折型模型三：旋转型模型四：一线三垂直型【类型一：平移型】【典例1】如图已知点E、C在线段BF上BE=CF AB∥DE∠ACB=∠F.求证：.【解答】证明：∵AB∥DE∴∠B=∠DEF∵BE=CF∴BE+EC=CF+EC即BC=EF.∴在△ABC和△DEF中{∠B=∠DEF BC=EF ∠ACB=∠F∴△ABC≅△DEF(ASA).【变式1-1】如图已知Rt△ABC与Rt△DEF中△A＝△D＝90° 点B、F、C、E在同一直线上且AB＝DE BF＝CE 求证：△B＝△E．【解答】证明：∵BF=CE BF+FC=BC CE+CF=EF∴BC=EF在Rt△ABC和Rt△DEF中∵{BC=EFAB=DE∴Rt△ABC≌Rt△DEF(HL)∴∠B=∠E．【变式1-2】如图点A、B、C、D在一条直线上EA//FB EC//FD EA=FB．求证：AB=CD．【解答】证明：∵EA∥FB∴∠A=∠FBD∵EC∥FD∴∠D=∠ECA 在△EAC和△FBD中{∠ECA=∠D∠A=∠FBDAE=BF∴△EAC≌△FBD(AAS)∴AC=BD∴AB+BC=BC+CD∴AB=CD．【变式1-3】如图点B C E F在同一直线上BE=CF AC⊥BC DF⊥EF垂足分别为C F AB=DE．求证：AC=DF．【解答】证明：∵BE=CF∴BE−CE=CF−CE即BC=EF在Rt△ABC和Rt△DEF中{BC=EFAB=DE∴Rt△ABC△Rt△DEF（HL）∴AC=DF．【类型二：翻折型】【典例2】已知△A＝△D BC平分△ABD 求证：AC＝DC．【解答】解：∵BC平分△ABD ∴△ABC＝△DBC在△BAC和△BDC中{∠A=∠D ∠ABC=∠DBC BC=BC∴△BAC△△BDC∴AC＝DC．【变式2-1】如图已知BD是∠ABC的角平分线AB=CB．求证：△ABD≌△CBD．【解答】证明：∵BD是∠ABC的角平分线（已知）∴∠ABD=∠CBD（角平分线定义）在△ABC与△CBD中∵{AB=CB(已知)∠ABD=∠CBD(已证)BD=BD(公共边)∴△ABD≌△CBD(SAS)．【变式2-2】已知：如图线段BE、DC交于点O 点D在线段AB上点E在线段AC 上AB＝AC AD＝AE．求证：△B＝△C．【解答】解：在△AEB和△ADC中{AB=AC ∠A=∠A AE=AD∴△AEB△△ADC（SAS）∴△B=△C．【变式2-3】已知：如图△ABC＝△DCB △1＝△2.求证AB＝DC.【解答】证明：如图记AC BD的交点为O∵△ABC＝△DCB △1＝△2又∵△OBC＝△ABC−△1 △OCB＝△DCB−△2∴△OBC＝△OCB∴OB＝OC在△ABO和△DCO中{∠1=∠2OB=OC∠AOB=∠DOC∴△ABO△△DCO（ASA）∴AB＝DC.【类型三：旋转型】【典例3】已知：如图AD BE相交于点O AB△BE DE△AD 垂足分别为B D OA=OE．求证：△ABO△△EDO．【解答】证明：∵AB△BE DE△AD∴△B=△D=90°．在△ABO和△EDO中{∠B=∠D ∠AOB=∠EOD OA=OE∴△ABO△△EDO．【变式3】如图已知线段AC BD相交于点E AE＝DE BE＝CE求证：△ABE△△DCE．【解答】证明：在△ABE和△DCE中{AE=DE ∠AEB=∠DEC BE=CE∴△ABE△△DCE（SAS）【典例4】如图CA=CD ∠1=∠2 BC=EC求证：∠B=∠E.【解答】证明：∵△1＝△2∴△1＋△ECA＝△2＋△ECA 即△ACB＝△DCE 在△ABC和△DEC中{CA＝CD∠ACB＝∠DCEBC＝EC∴△ABC△△DEC（SAS）∴∠B=∠E.【变式4】如图△ABC中点E在BC边上AE＝AB 将线段AC绕A点旋转到AF 的位置使得△CAF＝△BAE 连接EF EF与AC交于点G.（1）求证：EF＝BC；（2）若△ABC＝65° △ACB＝28° 求△FGC的度数.【解答】（1）证明：∵△CAF＝△BAE∴△CAF+△CAE＝△BAE+△CAE 即△EAF=△BAC∵AE＝AB AC=AF∴△EAF△△BAC∴EF＝BC；（2）解：∵△EAF△△BAC∴△AEF=△ABC＝65°∵AB=AE∴△AEB=△ABC＝65°∴△FEC=180°-△AEB-△AEF＝50°∴△FGC=△FEC+△ACB=78°.【类型四：一线三垂直型】【典例5】如图AB＝AC直线l经过点A BM△l CN△l垂足分别为M、N BM＝AN．（1）求证：MN＝BM+CN；（2）求证：△BAC＝90°．【解答】（1）证明：∵BM△直线l CN△直线l ∴△AMB＝△CNA＝90°在Rt△AMB和Rt△CNA中{AB=CABM=AN∴Rt△AMB△Rt△CNA（HL）∴BM＝AN CN＝AM∴MN＝AM+AN＝BM+CN；（2）由（1）得：Rt△AMB△Rt△CNA∴△BAM＝△ACN∵△CAN+△ACN＝90°∴△CAN+△BAM＝90°∴△BAC＝180°﹣90°＝90°．【变式5-1】课间小明拿着老师的等腰三角板玩不小心掉在两墙之间如图所示：（1）求证：△ADC△△CEB；（2）已知DE=35cm 请你帮小明求出砌墙砖块的厚度a的大小（每块砖的厚度相同）【解答】（1）证明：由题意得：AC＝BC △ACB＝90° AD△DE BE△DE∴△ADC＝△CEB＝90°∴△ACD＋△BCE＝90° △ACD＋△DAC＝90°∴△BCE＝△DAC在△ADC和△CEB中{∠ADC＝∠CEB ∠DAC＝∠BCE AC＝BC∴△ADC△△CEB（AAS）；（2）解：由题意得：∵一块墙砖的厚度为a∴AD＝4a BE＝3a由（1）得：△ADC△△CEB∴DC＝BE＝3a AD＝CE＝4a∴DC＋CE＝BE＋AD＝7a＝35∴a＝5答：砌墙砖块的厚度a为5cm．【变式5-2】在△ABC中∠ACB=90°AC=BC直线MN经过点C且AD⊥MN于D BE⊥MN于E.（1）当直线MN绕点C旋转到图1的位置时①求证：△ADC△ △CEB；②求证：DE=AD+BE；（2）当直线MN绕点C旋转到图2的位置时（1）中的结论②还成立吗？若成立请给出证明；若不成立说明理由.【解答】（1）证明：①∵AD△MN BE△MN∴△ADC=△BEC=90°∵△ACB=90°∴△ACD+△BCE=90° △DAC+△ACD=90°∴△DAC=△BCE又∵AC=BC∴△ADC△ △CEB；②∵△ADC△ △CEB∴CD=BE AD=CE∵DE=CE+CD∴DE=AD+BE；（2）解：DE=AD+BE不成立此时应有DE=AD－BE 理由如下：∵BE△MN AD△MN∴△ADC=△BEC=90°∴△EBC+△ECB=90°∵△ACB=90°∴△ECB+△ACE=90°∴△ACD=△EBC又∵AC=BC∴△ADC△ △CEB∴AD=CE CD=BE∵DE=CE－CD∴DE=AD－BE.1．如图在△ABC和△CDE中点B、D、C在同一直线上已知△ACB=△E AC=CE AB∥DE 求证：△ABC△△CDE．【解答】证明：∵AB∥DE ∴∠B=∠EDC在△ABC和△CDE中{∠B=∠EDC ∠ACB=∠E AC=CE∴△ABC≌△CDE(AAS)．2．如图AC和BD相交于点O OA=OC DC△AB．求证DC=AB．【解答】证明：∵DC△AB∴△D=△B在△COD与△AOB中{∠D=∠B ∠DOC=∠BOA OC=OA∴△COD△△AOB（AAS）∴DC=AB．3．如图点B、F、C、E在同一条直线上△B＝△E AB＝DE BF＝CE．求证：AC ＝DF．【解答】证明：∵BF＝CE∴BＦ＋FC＝CE＋FC 即BC＝EF在△ABC和△DEF中{AB=DE ∠B=∠E BC=EF∴△ABC△△DEF（SAS）∴AC＝DF．4．如图等边△ABC的内部有一点D 连接BD 以BD为边作等边△BDE连接AD CE 求证：AD=CE．【解答】证明：∵△ABC和△DBE为等边三角形∴△ABC =△DBE=60°AB=BC DB=EB∴△ABC−△DBC=△DBE−△DBC即△ABD=△CBE在△ABD和△CBE中{AB=BC∠ABD=∠CBE BD=EB∴△ABD≌△CBE(SAS)∴AD=CE5．如图点E F在BC上BE＝CF △A＝△D △B＝△C 求证：AB＝DC.【解答】证明：∵点E F在BC上BE＝CF ∴BE+EF＝CF+EF 即BF＝CE；在△ABF和△DCE中{∠A=∠D ∠B=∠C BF=CE∴△ABF△△DCE（AAS）∴AB＝CD（全等三角形的对应边相等）.6．如图点B、C、E、F在一条直线上AB=CD AE=DF BF=CE求证：∠A=∠D.【解答】证明：∵BF=CE∴BF+EF=CE+EF即BE=CF在△ABE和△DCF中{AB=DCBE=CFAE=DF∴△ABE△△DCF．∴∠A=∠D7．如图已知AB、CD相交于点O 且AD=CB AB=CD．求证：△A=△C．【解答】证明：连接BD 如图在△ABD和△CDB中∵AD=CB AB=CD BD=DB∴△ABD△△CDB（SSS）∴△A=△C．8．已知：如图A、C、F、D在同一条直线上且AB//DE AF＝DC AB＝DE求证：△ABC△△DEF．【解答】证明：∵AB△DE∴△A＝△D∵AF＝CD∴AD+CF＝CF+DF∴AC＝DF在△ABC和△DEF中{AC=DF ∠A=∠D AB=DE∴△ABC△△DEF（SAS）．9．如图：点E、F在BC上BE=CF AB=DC∠B=∠C AF与DE交于点G.过点G作GH⊥BC垂足为H.（1）求证：△ABF≌△DCE（2）求证：∠EGH=∠FGH【解答】（1）证明：∵BE=CF∴BF=CE在△ABF和△DCE中{AB=DC ∠B=∠C BF=CE∴△ABF△△DCE（SAS）.（2）证明：∵△ABF△△DCE∴△AFE=△DEC∴EG=GF∵GH△BC∴△EGH=△FGH.10．如图AD平分∠BAC ∠ADB=∠ADC.（1）求证：△ABD⊆△ACD：（2）若∠B=25° ∠BAC=40°求∠BDC的度数.【解答】（1）证明：∵AD平分∠BAC ∴∠BAD=∠CAD.又∵AD=DA ∠ADB=∠ADC ∴△ABD≅△ACD(ASA)（2）解：∵∠BAD=∠CAD ∠BAC=40°∴∠BAD=∠CAD=12∠BAC=20°.又∵∠B=25°∴∠ADB=180°−∠B−∠BAD=135°.又∵△ABD≅△ACD ∴∠ADC=∠ADB=135°.又∵∠ADB+∠ADC+∠BDC=360°∴∠BDC=90°.11．如图在四边形ABCD中E是CB上一点分别延长AE DC相交于点F AB= CF ∠CEA=∠B+∠F．（1）求证：∠EAB=∠F；（2）若BC=10求BE的长．【解答】（1）证明：∵∠CEA是△ABE的外角∴∠CEA=∠B+∠EAB．又∵∠CEA=∠B+∠F∴∠EAB=∠F．（2）解：在△ABE和△FCE中{AB=FC ∠EAB=∠F ∠AEB=∠FEC∴△ABE△△FCE．∴BE=CE．∵BC=10∴BE=5．12．如图AB⊥BE DE⊥BE垂足分别为点B E且AB=DE BF=CE点B F C E在同一条直线上AC DF相交于点G．求证：（1）ΔABC≌ΔDEF；（2）AG=DG．【解答】（1）解：∵AB⊥BE DE⊥BE∴∠B=∠E=90°∵BF=CE∴BF+FC=CE+FC即BC=EF在ΔABC和ΔDEF中{AB=DE∠B=∠EBC=EF∴ΔABC≌ΔDEF(SAS)（2）解：由（1）全等可知：AC=DF ∠ACB=∠DFE∴CG=FG13．如图已知△A＝△D AB＝DB 点E在AC边上△AED＝△CBE AB和DE相交于点F．（1）求证：△ABC△△DBE．（2）若△CBE＝50° 求△BED的度数．【解答】（1）证明：∵△A＝△D △AFE＝△BFD∴△ABD＝△AED又∵△AED＝△CBE∴∠ABD=∠CBE∴△ABD+△ABE＝△CBE+△ABE即△ABC＝△DBE在△ABC和△DBE中{∠A=∠DAB=DB ∠ABC=∠DBE∴△ABC△△DBE（ASA）；（2）解：∵△ABC△△DBE∴BE＝BC∴△BEC＝△C∵△CBE＝50°∴△BEC＝△C＝65°．∴AG=DG14．已知：如图点A D C B在同一条直线上AD=BC AE=BF CE=DF求证：（1）AE△FB（1）DE=CF.【解答】（1）证明：在△ADE和△BCF中{AE＝BF∠A＝∠BAD＝BC∴△ADE△△BCF（SAS）∴DE=CF．15．如图在△ABC中AB＝BC BE平分△ABC AD为BC边上的高且AD＝BD．（1）求证：△ABE=△CAD（2）试判断线段AB与BD DH之间有何数量关系并说明理由．【解答】（1）证明：∵AB＝BC BE平分△ABC∴BE△AC∴△BEA＝90°＝△ADB∵△CAD+△BEA+△AHE＝180° △HBD+△ADB+△BHD＝180° △AHE＝△BHD∴△HBD＝△CAD∵△HBD＝△ABE∴△ABE=△CAD（2）解：AB＝BD+DH理由是：∵在△BDH和△ADC中{∠2=∠3 BD=AD∠BDH=∠ADC=90°∴△BDH△△ADC（ASA）∴DH＝DC∴BC＝BD+DC＝BD+DH∵AB＝BC∴AB＝BD+DH．16．如图1 AC=BC CD=CE △ACB=△DCE=α AD、BE相交于点M.（1）求证：BE=AD；（2）直接用含α的式子表示△AMB的度数为（3）当α=90°时取AD BE的中点分别为点P、Q 连接CP CQ PQ 如图2 判断△CPQ的形状并加以证明.【解答】（1）证明：如图1∵△ACB=△DCE=α∴△ACD=△BCE在△ACD和△BCE中{CA=CB ∠ACD=∠BCE CD=CE∴△ACD△△BCE（SAS）∴BE=AD；（2）α（3）解：△CPQ为等腰直角三角形证明：如图2 由（1）可得BE=AD∵AD BE的中点分别为点P、Q∴AP=BQ∵△ACD△△BCE∴△CAP=△CBQ在△ACP和△BCQ中{CA=CB ∠CAP=∠CBQ AP=BQ∴△ACP△△BCQ（SAS）∴CP=CQ 且△ACP=△BCQ 又∵△ACP+△PCB=90°∴△BCQ+△PCB=90°∴△PCQ=90°∴△CPQ为等腰直角三角形.。

人教版八年级数学上册证明三角形全等的常见题型全等三角形是初中几何的重要内容之一，全等三角形的学习是几何入门最关键的一步，这部分内容学习的好坏直接影响着今后的学习。

而一些初学的同学，虽然学习了几种判定三角形全等的公理和推论，但往往仍不知如何根据已知条件证明两个三角形全等。

在辅导时可以抓住以下几种证明三角形全等的常见题型，进行分析。

一、已知一边与其一邻角对应相等1．证已知角的另一边对应相等，再用SAS证全等。

例1已知：如图1，点E、F在BC上，BE=CF，AB=DC，∠B=∠C .求证：AF=DE。

证明∵BE=CF（已知），∴BE+ EF=CF+EF，即BF=CE。

在△ABF和△DCE中，∴△ABF≌△DCE（SAS）。

∴ AF=DE（全等三角形对应边相等）。

2．证已知边的另一邻角对应相等，再用ASA证全等。

例2已知：如图2，D是△ABC的边AB上一点，DF交AC于点E，DE=FE，FC∥AB。

求证：AE=CE。

证明∵ FC∥AB（已知），∴∠ADE=∠CFE（两直线平行，内错角相等）。

在△ADE和△CFE中，∴△ADE≌△CFE（ASA）.∴ AE=CE（全等三角形对应边相等）3．证已知边的对角对应相等，再用AAS证全等。

例3（同例2）.证明∵ FC∥AB（已知），∴∠A=∠ECF（两直线平行，内错角相等）.在△ADE和△CFE中，∴△ADE≌△CFE（AAS）.∴ AE=CE（全等三角形对应边相等）。

二、已知两边对应相等1．证两已知边的夹角对应相等，再用SAS证等。

例4已知：如图3，AD=AE，点D、E在BCBD=CE，∠1=∠2。

求证：△ABD≌△ACE.证明∵∠1=∠2（已知），∠ADB=180°-∠1，∠AEC=180°-∠2（邻补角定义），∴∠ADB = ∠AEC，在△ABD和△ACE中，∴△ABD≌△ACE（SAS）.2．证第三边对应相等，再用SSS证全等。

例5已知：如图4，点A、C、B、D在同一直线AC=BD，AM=CN，BM=DN。

初中数学（人教版）八年级上知识点最全总结第十一章全等三角形一．知识框架二．知识概念1. 全等三角形：两个三角形的形状、大小、都一样时，其中一个可以经过平移、旋转、对称等运动（或称变换）使之与另一个重合，这两个三角形称为全等三角形。

2 ．全等三角形的性质：全等三角形的对应角相等、对应边相等。

3. 三角形全等的判定公理及推论有：（1 ）“ 边角边” 简称“SAS”（2 ）“ 角边角” 简称“ASA”（3 ）“ 边边边” 简称“SSS”（4 ）“ 角角边” 简称“AAS”（5 ）斜边和直角边相等的两直角三角形（HL ）。

4. 角平分线推论：角的内部到角的两边的距离相等的点在叫的平分线上。

5. 证明两三角形全等或利用它证明线段或角的相等的基本方法步骤：①、确定已知条件（包括隐含条件，如公共边、公共角、对顶角、角平分线、中线、高、等腰三角形、等所隐含的边角关系），②、回顾三角形判定，搞清我们还需要什么，③、正确地书写证明格式( 顺序和对应关系从已知推导出要证明的问题). 在学习三角形的全等时，教师应该从实际生活中的图形出发，引出全等图形进而引出全等三角形。

通过直观的理解和比较发现全等三角形的奥妙之处。

在经历三角形的角平分线、中线等探索中激发学生的集合思维，启发他们的灵感，使学生体会到集合的真正魅力。

第十二章轴对称一．知识框架二．知识概念1. 对称轴：如果一个图形沿某条直线折叠后，直线两旁的部分能够互相重合，那么这个图形叫做轴对称图形；这条直线叫做对称轴。

2. 性质：（1 ）轴对称图形的对称轴，是任何一对对应点所连线段的垂直平分线。

（2 ）角平分线上的点到角两边距离相等。

（3 ）线段垂直平分线上的任意一点到线段两个端点的距离相等。

（4 ）与一条线段两个端点距离相等的点，在这条线段的垂直平分线上。

（5 ）轴对称图形上对应线段相等、对应角相等。

3. 等腰三角形的性质：等腰三角形的两个底角相等，（等边对等角）4. 等腰三角形的顶角平分线、底边上的高、底边上的中线互相重合，简称为“三线合一”。

八年级上册数学全等三角形模型一、全等三角形的概念。

1. 定义。

- 能够完全重合的两个三角形叫做全等三角形。

重合的顶点叫做对应顶点，重合的边叫做对应边，重合的角叫做对应角。

- 例如，在△ABC和△DEF中，如果△ABC经过平移、旋转、翻折等变换后能与△DEF完全重合，那么△ABC和△DEF就是全等三角形，点A与点D、点B与点E、点C 与点F是对应顶点，AB与DE、BC与EF、AC与DF是对应边，∠A与∠D、∠B与∠E、∠C与∠F是对应角。

2. 表示方法。

- 全等用符号“≌”表示，读作“全等于”。

例如，△ABC≌△DEF，表示△ABC 和△DEF全等。

书写时要注意对应顶点的字母写在对应的位置上。

二、全等三角形的性质。

1. 对应边相等。

- 如果△ABC≌△DEF，那么AB = DE，BC = EF，AC = DF。

- 这一性质可以用来求解三角形中边的长度。

例如，已知△ABC≌△DEF，AB = 5cm，EF = 7cm，求BC的长度。

因为BC与EF是对应边，且△ABC≌△DEF，所以BC=EF = 7cm。

2. 对应角相等。

- 如果△ABC≌△DEF，那么∠A = ∠D，∠B = ∠E，∠C = ∠F。

- 利用这个性质可以求解三角形中的角的度数。

已知△ABC≌△DEF，∠A = 30°，求∠D的度数。

由于∠A与∠D是对应角，且△ABC≌△DEF，所以∠D = ∠A = 30°。

三、全等三角形的判定模型（人教版八年级上册）1. SSS（边边边）判定模型。

- 判定定理：三边对应相等的两个三角形全等（简写成“SSS”）。

- 示例：在△ABC和△DEF中，AB = DE，BC = EF，AC = DF，那么△ABC≌△DEF。

- 应用场景：当已知两个三角形的三边长度分别相等时，就可以直接判定这两个三角形全等。

例如，已知一个三角形的三边分别为3cm、4cm、5cm，另一个三角形的三边也分别为3cm、4cm、5cm，那么这两个三角形全等。