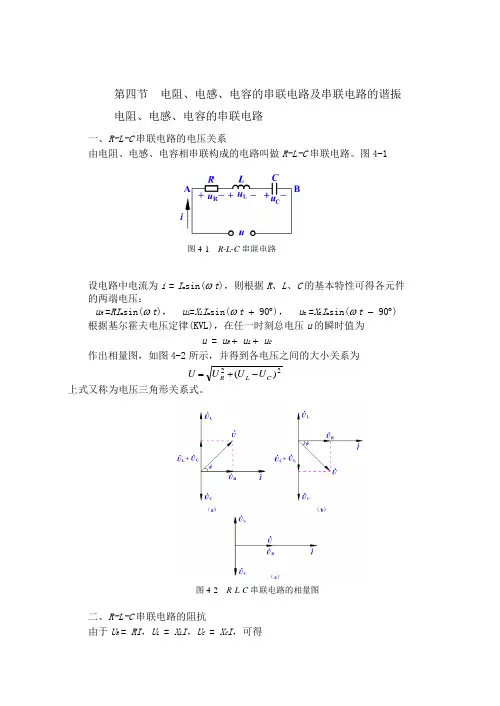
第四节 电阻、电感、电容的串联电路及串联电路的谐振 电阻、电感、电容的串联电路一、R-L-C 串联电路的电压关系由电阻、电感、电容相串联构成的电路叫做R-L-C 串联电路。
图4-1设电路中电流为i = I msin(ω t )，则根据R 、L 、C 的基本特性可得各元件的两端电压：u R =RI m sin(ω t )， u L =X L I m sin(ω t + 90︒)， u C =X C I m sin(ω t - 90︒) 根据基尔霍夫电压定律(KVL)，在任一时刻总电压u 的瞬时值为u = u R + u L + u C作出相量图，如图4-2所示，并得到各电压之间的大小关系为22)(C L R U U U U -+=上式又称为电压三角形关系式。
二、R-L-C 串联电路的阻抗由于U R = RI ，U L = X L I ，U C = X C I ，可得图4-1 R-L-C 串联电路图4-2 R -L -C 串联电路的相量图2222)()(C L C L R X X R I U U U U -+=-+=令2222)(X R X X R IU Z C L +=-+==上式称为阻抗三角形关系式，|Z |叫做R-L-C 串联电路的阻抗，其中X = X L - X C 叫做电抗。
阻抗和电抗的单位均是欧姆(Ω)。
阻抗三角形的关系如图4-3所示。
由相量图可以看出总电压与电流的相位差为RX R X X U U U C L R C L arctan arctan arctan =-=-=ϕ 上式中 ϕ 叫做阻抗角。
三、R-L-C 串联电路的性质根据总电压与电流的相位差(即阻抗角 ϕ)为正、为负、为零三种情况，将电路分为三种性质。
1. 感性电路：当X > 0时，即X L > X C ，ϕ > 0，电压u 比电流i 超前ϕ，称电路呈感性；2. 容性电路：当X < 0时，即X L < X C ，ϕ < 0，电压u 比电流i 滞后|ϕ|，称电路呈容性；3. 谐振电路：当X = 0时，即X L = X C ，ϕ = 0，电压u 与电流i 同相，称电路呈电阻性，电路处于这种状态时，叫做谐振状态。
解：(1) X L = 2πfL ≈ 140 Ω，X C = fC π21 ≈ 100 Ω，Ω=-+=50)(22C L X X R Z ，则图4-3 R-L-C 串联电路的阻抗三角形 例4-1 在R-L-C 串联电路中，交流电源电压U = 220 V ，频率f = 50 Hz ，R = 30 Ω，L = 445 mH ，C = 32 μF 。
试求：(1) 电路中的电流大小I ；(2) 总电压与电流的相位差 ϕ；(3) 各元件上的电压U R 、U L 、U C 。
A 4.4==ZU I (2) 1.533040arctan arctan ==-=R X X C L ϕ，即总电压比电流超前53.1︒，电路呈感性。
(3) U R = RI = 132 V ，U L = X L I = 616 V ，U C = X L I = 440 V 。
本例题中电感电压、电容电压都比电源电压大，在交流电路中各元件上的电压可以比总电压大，这是交流电路与直流电路特性不同之处。
四、R-L 串联与R-C 串联电路1．R-L 串联电路只要将R-L-C 串联电路中的电容C 短路去掉，即令X C = 0，U C = 0，则有关R-L-C 串联电路的公式完全适用于R-L 串联电路。
解：(1) X L = 2πfL ≈ 30 Ω，Ω=+=5022L X R Z ，则A 4==ZU I (2) U R = RI = 160 V ，U L = X L I = 120 V ，显然22LR U U U += 。
(3) 9.364030arctan arctan ===R X L ϕ，即总电压u 比电流i 超前36.9︒，电路呈感性。
2．R-C 串联电路只要将R-L-C 串联电路中的电感L 短路去掉，即令X L = 0，U L = 0，则有关R-L-C 串联电路的公式完全适用于R-C 串联电路。
解：(1) 由V 10022.141,10080122==Ω=+=Ω==U X R Z C X C C ，ω，则电流为A 1==ZU I 例4- 2在R-L 串联电路中，已知电阻R = 40 Ω，电感L = 95.5 mH ，外加频率为f = 50 Hz 、U = 200 V 的交流电压源，试求：(1) 电路中的电流I ； (2) 各元件电压U R 、U L ；(3) 总电压与电流的相位差 ϕ 。
例4-3在R-C 串联电路中，已知：电阻R = 60 Ω，电容C = 20 μF ，外加电压为u = 141.2sin628t V 。
试求：(1) 电路中的电流I ；(2) 各元件电压U R 、U C ；(3) 总电压与电流的相位差 ϕ 。
(2) U R = RI = 60 V ，U C = X C I = 80 V ，显然 22CR U U U += 。
(3) 53.1)6080(arctan )arctan(C -=-=-=R X ϕ，即总电压比电流滞后53.1︒，电路呈容性。
串联电路的谐振工作在谐振状态下的电路称为谐振电路，谐振电路在电子技术与工程技术中有着广泛的应用。
谐振电路最为明显的特征是整个电路呈电阻性，即电路的等效阻抗为Z 0 = R ，总电压u 与总电流i 同相。
一、谐振频率与特性阻抗R-L-C 串联电路呈谐振状态时，感抗与容抗相等，即X L = X C ，设谐振角频率为 ω0， 则CL 001ωω=，于是谐振角频率为 LC10=ω 由于 ω0 = 2πf 0，所以谐振频率为LCf π=210 由此可见，谐振频率f 0只由电路中的电感L 与电容C 决定，是电路中的固有参数，所以通常将谐振频率f 0叫做固有频率。
电路发生谐振时的感抗或容抗叫做特性阻抗，用符号 ρ 表示，单位为欧姆(Ω)。
CL C L ===001ωωρ二、串联谐振电路的特点1．电路呈电阻性当外加电源u S 的频率f = f 0时，电路发生谐振，由于X L = X C ，则此时电路的阻抗达到最小值，称为谐振阻抗Z 0或谐振电阻R ，即Z 0 = |Z |max = R2．电流呈现最大谐振时电路中的电流则达到了最大值，叫做谐振电流I 0，即RU I S 0=3．电感L 与电容C 上的电压串联谐振时，电感L 与电容C 上的电压大小相等，即U L = U C = X L I 0 = X C I 0 = QU S式中Q 叫做串联谐振电路的品质因数，即CRR L R Q 001ωωρ=== R-L-C 串联电路发生谐振时，电感L 与电容C 上的电压大小都是外加电源电压U S 的Q 倍，所以串联谐振电路又叫做电压谐振。
一般情况下串联谐振电路都符合Q >>1的条件。
三、串联谐振的应用串联谐振电路常用来对交流信号的选择，例如接收机中选择电台信号，即调谐。
在R-L-C 串联电路中，阻抗大小22)1(CL R Z ωω-+=，设外加交流电源(又称信号源)电压u S 的大小为U S ，则电路中电流的大小为22S S)1(CL R U Z U I ωω-+= 由于则， 1 00S 0CRR L Q R U I ωω===， 20020)(11ωωωω-+=Q I I图4-4 R-L-C 串联电路的谐振特性曲线此式表达出电流大小与电路工作频率之间的关系，叫做串联电路的电流幅频特性。
电流大小I 随频率f 变化的曲线，叫做谐振特性曲线，如图8-7所示。
当外加电源u S 的频率f = f 0时，电路处于谐振状态；当f ≠ f 0时，称为电路处于失谐状态，若f < f 0，则X L < X C ，电路呈容性；若f > f 0，则X L > X C ，电路呈感性。
在实际应用中，规定把电流I 范围在(0.7071I 0 < I < I 0)所对应的频率范围(f 1 ~ f 2)叫做串联谐振电路的通频带(又叫做频带宽度)，用符号B 或 ∆f 表示，其单位也是频率的单位。
理论分析表明，串联谐振电路的通频带为Qf f f f B 012=-=∆= 频率f 在通频带以内 (即f 1 < f < f 2 )的信号，可以在串联谐振电路中产生较大的电流，而频率f 在通频带以外 (即f < f 1或f > f 2 )的信号，仅在串联谐振电路中产生很小的电流，因此谐振电路具有选频特性。
Q 值越大说明电路的选择性越好，但频带较窄；反之，若频带越宽，则要求Q 值越小，而选择性越差；即选择性与频带宽度是相互矛盾的两个物理量。
解： (1)kHz 50 40 MHz 2π21000======Q f B R L Q LCf ，，ω (2) I 0 = U /R = 1/9.4 = 0.106 mA ，U L0 = U C0 = QU = 40 mV(3) 当f = f 0 + ∆f = 2.2 MHz 时，B = 2∆f = 13.816 ⨯ 106 rad/sm A 014.072)1(22==Ω=-+=Z U ΙCL R Z ωω仅为谐振电流I 0的13.2%。
例4-4 设在R-L-C 串联电路中，L = 30 μH ，C = 211 pF ， R = 9.4 Ω，外加电源电压为u =2sin(2πf t ) mV 。
试求： (1) 该电路的固有谐振频率f 0与通频带B ； (2) 当电源频率f = f 0时(即电路处于谐振状态)电路中的谐振电流I 0、电感L 与电容C 元件上的电压U L 0、U C 0 ； (3) 如果电源频率与谐振频率偏差 ∆f = f - f 0 = 10% f 0 ，电路中的电流I 为多少？。
