《电工学》秦曾煌第六版第二章习题备课讲稿

《电工学》秦曾煌第六版上下册课后答案(同名17708)D[解] 首先根据基尔霍夫电流定律列出图2: 习题1.5.2图−I1 + I2 −I3=−3 + 1 −I3=可求得I3= −2mA, I3的实际方向与图中的参考方向相反。

根据基尔霍夫电流定律可得U3 = (30 + 10 ×103 ×3 ×10−3 )V =60V其次确定电源还是负载：1 从电压和电流的实际方向判定：电路元件3 80V元件30V元件电流I3从“+”端流出,故为电源;电流I2从“+”端流出，故为电源；电流I1从“+”端流出，故为负载。

2 从电压和电流的参考方向判别：电路元件3 U3和I3的参考方向相同P= U3I3 = 60 ×(−2) ×10−3W=−120 ×10−3W （负值），故为电源；80V元件U2和I2的参考方向相反P = U2I2 = 80 ×1 ×10−3W =80 ×10−3W （正值），故为电源；30V元件U1和I1参考方向相同P= U1I1 = 30 ×3 ×10−3 W = 90 ×10−3W （正值），故为负载。

两者结果一致。

最后校验功率平衡：电阻消耗功率:2 2= R1I1 = 10 ×3 mW = 90mWP R12 2= R2I2 = 20 ×1 mW = 20mWP R2电源发出功率:P E = U2I2 + U3I3 = (80 + 120)mW =200mW负载取用和电阻损耗功率:P = U1I1 + R1 I2 + R2I2 = (90 + 90 + 20)mW =200mW1 2两者平衡1.5.3有一直流电源，其额定功率PN= 200W ，额定电压U N= 50V 。

内阻R0 =0.5Ω，负载电阻R可以调节。

其电路如教材图1.5.1所示试求：1 额定工作状态下的电流及负载电阻；2 开路状态下的电源端电压；3 电源短路状态下的电流。

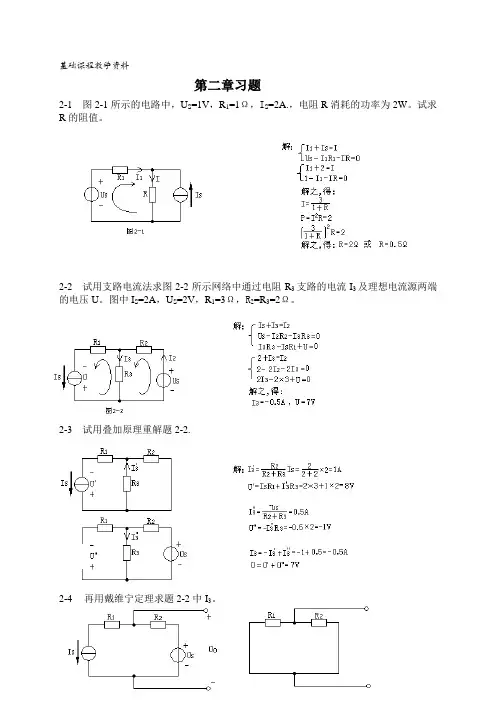
基础课程教学资料第二章习题2-1 图2-1所示的电路中，U S=1V，R1=1Ω，I S=2A.，电阻R消耗的功率为2W。

试求R的阻值。

2-2 试用支路电流法求图2-2所示网络中通过电阻R3支路的电流I3及理想电流源两端的电压U。

图中I S=2A，U S=2V，R1=3Ω，R2=R3=2Ω。

2-3 试用叠加原理重解题2-2.2-4再用戴维宁定理求题2-2中I3。

2-5 图2-3所示电路中,已知U S1=6V，R1=2Ω，I S=5A，U S2=5V，R2=1Ω，求电流I。

2-6 图2-4所示电路中，U S1=30V，U S2=10V，U S3=20V，R1=5kΩ，R2=2kΩ，R3=10kΩ，I S=5mA。

求开关S在位置1和位置2两种情况下，电流I分别为多少？2-7 图2-5所示电路中，已知U AB=0，试用叠加原理求U S的值。

2-8 电路如图2-6所示，试用叠加原理求电流I。

2-9 电路如图2-7所示，试用叠加原理求电阻R4上电压U的表达式。

2-10电路如图2-8所示,已知R1=Ω，R2=R3=2Ω，U S=1V，欲使I=0，试用叠加原理确定电流源I S的值。

2-11 画出图2-9所示电路的戴维宁等效电路。

2-12 图2-10所示的电路接线性负载时，U 的最大值和I的最大值分别是多少？2-13 电路如图2-11所示，假定电压表的内阻无穷大，电流表的内阻为零。

当开关S处于位置1时，电压表的读数为10V，当S处于位置2时，电流表的读数为5mA。

试问当S处于位置3SHI 4，电压表和电流表的读数各为多少？2-14 图2-12所示电路中，各电源的大小和方向均未知，只知每个电阻均为6Ω，又知当R=6Ω时，电流I=5A。

今欲使R支路电流I=3A，则R应该多大？2-15 图2-13所示电路中，N为线性有源二端网络，测得AB之间电压为9V，见图（a）；若连接如图（b）所示，可测得电流I=1A。

现连接如图（c）所示形式，问电流I为多少？2-16 电路如图2-14所示，已知R1=5Ω时获得的功率最大，试问电阻R是多大？本章小结1、支路电流法是分析和计算电路的基本方法，适用于任何电路。

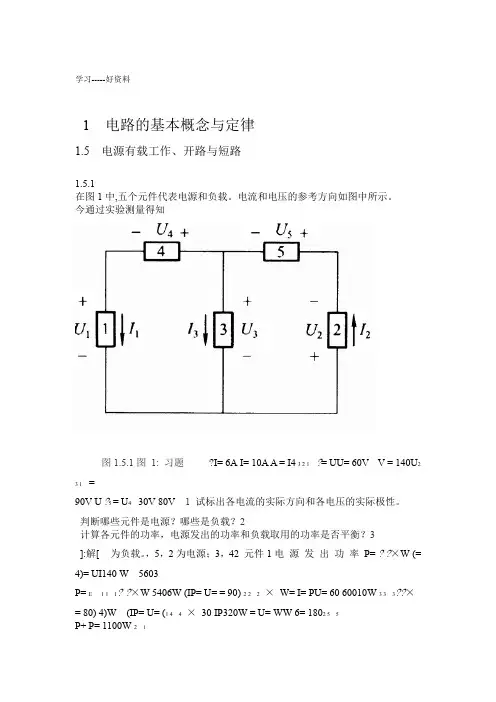
学习-----好资料1 电路的基本概念与定律1.5 电源有载工作、开路与短路1.5.1在图1中,五个元件代表电源和负载。

电流和电压的参考方向如图中所示。

今通过实验测量得知图1.5.1图1: 习题?I= 6A I= 10A A = I43 2 1 ?= UU= 60V V = 140U23 1 =90V U?5 = U4 30V 80V 1 试标出各电流的实际方向和各电压的实际极性。

判断哪些元件是电源？哪些是负载？2计算各元件的功率，电源发出的功率和负载取用的功率是否平衡？3]:解[为负载。

，5，2为电源；3，42 元件1电源发出功率P= ??×W (=4)= UI140 W 5603P= E 1 1 1??×W 5406W (IP= U= = 90) 2 2 2×W= I= PU= 60 60010W 3 3 3??×= 80) 4)W (IP= U= (1 4 4×30 IP320W = U= WW 6= 1802 5 5P+ P= 1100W 2 1负载取用功率P = P+ P+ P= 1100W 5 4 3两者平衡1.5.2在图2中，已知I和其两端I中的电流试确定电路元件mA= ImA= 3,1.33 12更多精品文档．学习-----好资料电压U，并说明它是电源还是负载。

校验整个电路的功率是否平衡。

3更多精品文档．学习-----好资料[解] 首先根据基尔霍夫电流定律列出图2: 习题1.5.2图?? = 0 + III 2 1 3?? = 0 I1 3 + 3可求得I的实际方向与图中的参考方向相反。

?I2mA, = 33根据基尔霍夫电流定律可得?3 3 ×××)10V = 60V = U(30 + 10 103 3其次确定电源还是负载：从电压和电流的实际方向判定：1电路元件3 电流I从“+”端流出,故为电源; 3电流I从“+”端流出，故为电源；80V元件2电流I从“+”端流出，故为负载。

第 2 章正弦交流电路第 2 章正弦交流电路2.1 正弦电压与电流2.2 正弦量的相量表示法2.3 单一参数的交流电路2.4 电阻、电感与电容元件串联的交流电路2.5 阻抗的串联与并联2.6 电路中的谐振2.7 功率因数的提高2.8 三相电路2.9 非正弦周期电压和电流第 2 章正弦交流电路在生产和生活中普遍应用正弦交流电,特别是三相电路应用更为广泛。

正弦交流电路是指含有正弦电源激励而且电路各部分所产生的电压和电流响应均按正弦规律变化的电路。

本章将介绍交流电路的一些基本概念、基本理论和基本分析方法,为后面学习交流电机、电器及电子技术打下基础。

本章还将讨论三相交流电路和非正弦周期电压和电流。

交流电路具有用直流电路的概念无法理解和无法分析的物理现象,因此在学习时注意建立交流的概念,以免引起错误。

U, I2.1 正弦电压与电流直流电路在稳定状态下电流、电压的大小和方向是不随时间变化的,如右上图所示。

正弦电压和电流是按正弦规律周期性tO变化的,其波形如右下图所示。

u i电路图上所标的方向是指它们的参考方向,即代表正半周的方向。

+负半周时,由于参考方向与实际方向相反,所以为负值。

Oti i实际+ +表征正弦量的三要素有R R方 u u? ?向幅值频率初相位正半周负半周2.1.1 频率与周期周期 T:正弦量变化一周所需要的时间;i频率 f:正弦量每秒内变化的次数;Im1f?t2TT/20 Tt22 ?f角频率:T?ITm [例]我国和大多数国家的电力标准频率是 50 Hz,试求其周期和角频率。

1T? 0.02 s[解]f 2?f 23.1450 rad/s 314 rad/s i2.1.2 幅值与有效值Im瞬时值是交流电任一时刻的值。

?t2用小写字母表示。

如 i、u、e 分别表0 T/2Tt示电流、电压、电动势的瞬时值。

?I最大值是交流电的幅值。

用大写m字母加下标表示。

如 I 、U 、E 。

m m miI sint?m i有效值是从电流的热效应来规定的。

1 电路的基本概念与定律电源有载工作、开路与短路电源发出功率P E =在图2中，已知I1= 3mA,I2 = 1mA.试确定电路元件3中的电流I3和其两端电压U3，并说明它是电源还是负载。

校验整个电路的功率是否平衡。

[解] 首先根据基尔霍夫电流定律列出图 2: 习题图−I1 + I2 −I3=−3 + 1 −I3=可求得I3= −2mA, I3的实际方向与图中的参考方向相反。

根据基尔霍夫电流定律可得U3 = (30 + 10 ×103 ×3 ×10−3 )V= 60V其次确定电源还是负载：1 从电压和电流的实际方向判定：电路元件3 80V元件30V元件电流I3从“+”端流出,故为电源;电流I2从“+”端流出，故为电源；电流I1从“+”端流出，故为负载。

2 从电压和电流的参考方向判别：电路元件3 U3和I3的参考方向相同P= U3I3 = 60 ×(−2) ×10−3W =−120 ×10−3W （负值），故为电源；80V元件U2和I2的参考方向相反P = U2I2 = 80 ×1 ×10−3W =80 ×10−3W （正值），故为电源；30V元件U1和I1参考方向相同P= U1I1 = 30 ×3 ×10−3 W =90 ×10−3W （正值），故为负载。

两者结果一致。

最后校验功率平衡：电阻消耗功率:2 2P R= R1I= 10 ×3 mW = 90mW12 2P R= R2I= 20 ×1 mW = 20mW2电源发出功率:P E = U2I2 + U3I3 = (80 + 120)mW =200mW负载取用和电阻损耗功率:P = U1I1 + R1 I2 + R2I2 = (90 + 90 + 20)mW =200mW1 2两者平衡基尔霍夫定律试求图6所示部分电路中电流I、I1和电阻R，设U ab = 0。

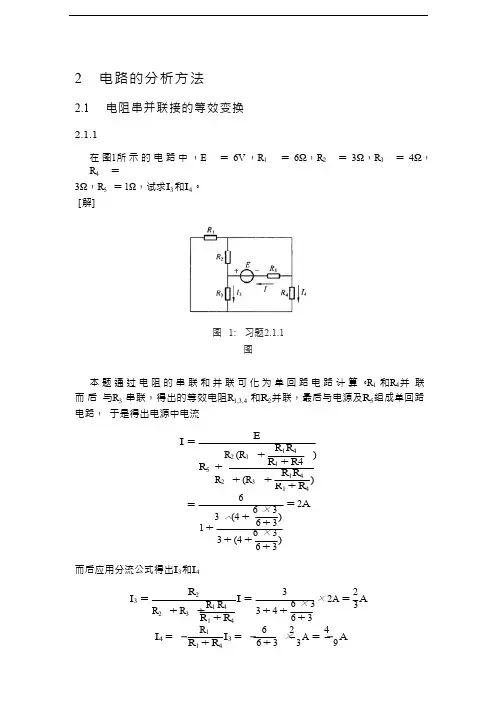
× R R R 2 电路的分析方法2.1 电阻串并联接的等效变换2.1.1在 图1所 示 的 电 路 中 ，E = 6V ，R 1 = 6Ω，R 2 = 3Ω，R 3 = 4Ω，R 4 =3Ω，R 5 = 1Ω，试求I 3 和I 4。

[解]图 1: 习题2.1.1图本 题 通 过 电 阻 的 串 联 和 并 联 可 化 为 单 回 路 电 路 计 算 。

R 1 和R 4并 联 而 后 与R 3 串联，得出的等效电阻R 1,3,4 和R 2并联，最后与电源及R 5组成单回路电路， 于是得出电源中电流EI =R 2 (R 3 +R 1R 4 )R 5 +R 1 + R 4R 1R 4R 2 + (R 3 +1 6) + R 4=3 (4 +6 × 3 )1 +6 + 3 6 × 3= 2A 3 + (4 + )6 + 3而后应用分流公式得出I 3和I 4I 3 =R 2R 1 R 4I = 36 × 3 2× 2A = 3 A R 2 + R 3 + 1+ R 4 3 + 4 + 6 + 3 R 16 2 4 I 4 = − 1 + R 4I 3 = − 6 + 3 × 3 A = − 9 AI4的实际方向与图中的参考方向相反。

2.1.2有 一 无 源 二 端 电 阻 网 络[图2（a ）]， 通 过 实 验 测 得 ： 当U = 10V 时 ，I =2A ；并已知该电阻网络由四个3Ω的电阻构成，试问这四个电阻是如何连接的？ [解]图 2: 习题2.1.2图 按题意，总电阻为U R = = I 10Ω = 5Ω2四个3Ω电阻的连接方法如图2（b ）所示。

2.1.3在图3中，R 1 = R 2 = R 3 = R 4 = 300Ω，R 5 = 600Ω，试求开关S 断开和闭和 时a 和b 之间的等效电阻。

[解]图 3: 习题2.1.3图 当开关S 断开时，R 1与R 3串联后与R 5 并联，R 2与R 4 串联后也与R 5并联，故U = × 5 = U = × 5 = 5 有R ab = R 5//(R 1 + R 3)//(R 2 + R 4 )1=1600 1 + +300 + 300 1 300 + 300= 200 Ω当S 闭合时，则有R ab = [(R 1//R 2) + (R 3//R 4 )]//R 51=1R +R 1 R 2 R 1 + R 2=1 +1 R 3 R 4 +R 3 + R 411 600 300 × 300 +300 × 300= 200 Ω300 + 300 300 + 3002.1.5[图4(a)]所示是一衰减电路，共有四挡。

图1: 习题1.5.1图I1 = −4A U1 = 140V U4 = −80V I2 = 6AU2 = −90V U5 =30VI3 = 10AU3 = 60V电工学秦曾煌课后答案全解 doc格式1 电路的基本概念与定律1.5 电源有载工作、开路与短路1.5.1在图1中,五个元件代表电源和负载。

电流和电压的参考方向如图中所示。

今通过实验测量得知1 试标出各电流的实际方向和各电压的实际极性。

2 判断哪些元件是电源？哪些是负载？3 计算各元件的功率，电源发出的功率和负载取用的功率是否平衡？[解]:2 元件1，2为电源；3，4，5为负载。

3 P1 = U1I1 = 140 ×(−4)W = −560WP2 = U2I2 = (−90) ×6W = −540WP3 = U3I3 = 60 ×10W = 600W P4 = U4I1 = (−80) ×(−4)W = 320W P5 = U5I2 =130 ×6W = 180WP1 + P2 = 1100W负载取用功率P = P3+ P4 + P5 = 1100W 两者平衡电源发出功率PE=1.5.2在图2中，已知I1= 3mA,I2 = 1mA.试确定电路元件3中的电流I3和其两端电压U3，并说明它是电源还是负载。

校验整个电路的功率是否平衡。

2[解] 首先根据基尔霍夫电流定律列出图2: 习题1.5.2图−I1 + I2 −I3= 0−3 + 1 −I3= 0可求得I3= −2mA, I3的实际方向与图中的参考方向相反。

根据基尔霍夫电流定律可得U3 = (30 + 10 ×103 ×3 ×10−3 )V = 60V 其次确定电源还是负载：1 从电压和电流的实际方向判定：电路元件380V元件30V元件电流I3从“+”端流出,故为电源;电流I2从“+”端流出，故为电源；电流I1从“+”端流出，故为负载。

电工学秦曾煌(第六版)上册_第二章主页目录第2章电路的分析方法2.12.22.32.42.52.6电阻串并联连接的等效变换电阻星型联结与三角型联结的等效变换电源的两种模型及其等效变换支路电流法结点电压法叠加原理2.7戴维宁定理与诺顿定理2.8受控源电路的分析第2章电路的分析方法本章要求：1.掌握支路电流法、叠加原理和戴维宁定理等电路的基本分析方法;2.了解实际电源的两种模型及其等效变换;3.了解非线性电阻元件的伏安特性及静态电阻、动态电阻的概念，以及简单非线性电阻电路的图解分析法。

退出2.1.1电阻的串联I2.1电阻串并联连接的等效变换2.1.2电阻的并联I+I1U–I+U–RI2R1R2(3)等效电阻的倒数等于各电阻倒数之和；111RR1R2(4)并联电阻上电流的分配与电阻成反比。

两电阻并联时的分流公式：特点:(1)各电阻联接在两个公共的结点之间；(2)各电阻两端的电压相同；应用：分流、调节电流等。

R2I1IR1R22.1.3电阻混联电路的计算例:电路如图,求U=解：211R'=—153+R"=—+441VU1–R'1–U1=——某412+R'=11VR"某U=3VU2=——2+R"11得U=——某U2=1V2+1R'2+1U2–2+1U–R"退出例1:图示为变阻器调节负载电阻RL两端电压的分压电路。

RL=50,U=220V中间环节是变阻器，其规格是100、3A。

今把它平分为四段，在图上用a,b,c,d,e点标出。

求滑动点分别在a,c,d,e四点时,负载和变阻器各段所通过的电流及负载电压,并就流过变阻器的电流与其额定电流比较说明使用时的安全问题。

解:(1)在a点：UL=0VIea+IL=0AU220A2.2ARea100U–edcbaIL+ULRL–退出解:(2)在c点：等效电阻R为Rca与RL并联，+e再与Rec串联，即ILdRcaRL5050Uc+RRec50bURRcaRL5050LaL––75U220Iec2.93AR752.93ILIca1.47A2ULRLIL501.4773.5V注意，这时滑动触点虽在变阻器的中点，解:(3)在d点：解:(4)在e点：U220Iea2.2ARea100U220IL4.4ARL50+UULU220V–edcbaIL+URLL–退出2.2电阻星形联结与三角形联结的等换ACDBAROCDROBIaRaIbIcaRcY-等效变换CIaaRabRbcRcabbRbIbIcC电阻Y形联结2.2电阻星形联结与三角形联结的等效变换IaIaRaaaRabRbcRcabIbIcbRcY-等效变换CRbIbIcC电阻Y形联结电阻形联结2.2电阻星形联结与三角形联结的等效变换IaIaRaaaRabRbcRcab IbIcbRcY-等效变换CRbIbIc电阻Y形联结条件电阻形联结据此可推出两者的关系2.2电阻星形联结与三角形联结的等效变换IaIaRaIbIcRabRbcRcaaRcY-等效变换CaRabRbcRcabRb YRaRbRbRcRcRaRcRaRbRbRcRcRaRaRaRbRbRcRcRaRbIbIcC退出2.2电阻星形联结与三角形联结的等效变换IaRaaIaaRabRbcRcab IbIcbRcY-等效变换CIbIcC对图示电路求总电阻R12例1:112R1221C212D10.8R120.422110.410.82.411.4R12R122.684由图：2例2:计算下图电路中的电流I1I14d4 a8I14d5aRaRccc5+–12Vb4Rbb+–12V解：例2:计算下图电路中的电流I1I14d4a8I14d5aRaRccc5+–12Vb4Rbb+–12V解：R(42)(51)Ω2Ω5Ω(42)(51)5112I1A1.2A42515退出+ER0I+理想电压源(恒压源)I+E_+U_ERLOUI2.3.2电流源模型电流源是由电流IS和内阻R0并联的电源的电路模型。

基础课程教学资料第二章习题2-1 图2-1所示的电路中，U S=1V，R1=1Ω，I S=2A.，电阻R消耗的功率为2W。

试求R的阻值。

2-2 试用支路电流法求图2-2所示网络中通过电阻R3支路的电流I3及理想电流源两端的电压U。

图中I S=2A，U S=2V，R1=3Ω，R2=R3=2Ω。

2-3 试用叠加原理重解题2-2.2-4再用戴维宁定理求题2-2中I3。

2-5 图2-3所示电路中,已知U S1=6V，R1=2Ω，I S=5A，U S2=5V，R2=1Ω，求电流I。

2-6 图2-4所示电路中，U S1=30V，U S2=10V，U S3=20V，R1=5kΩ，R2=2kΩ，R3=10kΩ，I S=5mA。

求开关S在位置1和位置2两种情况下，电流I分别为多少？2-7 图2-5所示电路中，已知U AB=0，试用叠加原理求U S的值。

2-8 电路如图2-6所示，试用叠加原理求电流I。

2-9 电路如图2-7所示，试用叠加原理求电阻R4上电压U的表达式。

2-10电路如图2-8所示,已知R1=Ω，R2=R3=2Ω，U S=1V，欲使I=0，试用叠加原理确定电流源I S的值。

2-11 画出图2-9所示电路的戴维宁等效电路。

2-12 图2-10所示的电路接线性负载时，U 的最大值和I的最大值分别是多少？2-13 电路如图2-11所示，假定电压表的内阻无穷大，电流表的内阻为零。

当开关S处于位置1时，电压表的读数为10V，当S处于位置2时，电流表的读数为5mA。

试问当S处于位置3SHI 4，电压表和电流表的读数各为多少？2-14 图2-12所示电路中，各电源的大小和方向均未知，只知每个电阻均为6Ω，又知当R=6Ω时，电流I=5A。

今欲使R支路电流I=3A，则R应该多大？2-15 图2-13所示电路中，N为线性有源二端网络，测得AB之间电压为9V，见图（a）；若连接如图（b）所示，可测得电流I=1A。

现连接如图（c）所示形式，问电流I为多少？2-16 电路如图2-14所示，已知R1=5Ω时获得的功率最大，试问电阻R是多大？本章小结1、支路电流法是分析和计算电路的基本方法，适用于任何电路。

本文由orca123456贡献pdf文档可能在WAP端浏览体验不佳。

建议您优先选择TXT，或下载源文件到本机查看。

目录第 2章章电路的分析方法第2.1.1题第2.1.2题第2.1.3题第2.1.5题第2.1.6题第2.1.7题第2.1.8题第2.3.1题第2.3.2题第2.3.4题第2.4.1题第2.4.2题第2.5.1题第2.5.2题第2.5.3题第2.6.1题第2.6.2题第2.6.3题第2.6.4题第2.7.1题第2.7.2题第2.7.5题第2.7.7题第2.7.8题第2.7.9题第2.7.10题第2.7.11题 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3 3 3 4 4 5 6 6 7 8 8 9 9 第2.1节电阻串并联接的等效变换 . . . . . . . . . . . . . . . . . . . . . 第2.3节电源的两种模型及其等效变换 . . . . . . . . . . . . . . . . . .第2.4节支路电流法 . . . . . . . . . . . . . . . . . . . . . . . . . . . .10 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .10 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .11 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .12 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .13 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .14 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .14 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .15 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .16 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .18 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .19 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .19 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .20 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .21 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .22 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .22 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .23 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 24第2.5节结点电压法 . . . . . . . . . . . . . . . . . . . . . . . . . . . .12 第2.6节叠加定理 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .14第2.7节戴维南定理与诺顿定理 . . . . . . . . . . . . . . . . . . . . . .19 1List of Figures1 习题2.1.1图 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .2 习题2.1.2图 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .3 习题2.1.3图 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .4 习题2.1.5图 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .5 习题2.1.7图 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .6 习题2.1.8图 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .7 习题2.3.1图 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .8 习题2.3.2图 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .9 习题2.3.4图 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .3 4 4 6 7 7 8 9 910 习题2.4.1图 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .10 11 习题2.4.2图 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .11 12 习题2.5.1图 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .13 13 习题2.5.2图 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .13 14 习题2.5.3图 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .14 15 习题2.6.1图 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .15 16 习题2.6.2图 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .16 17 习题2.6.3图 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .17 18 习题2.6.4图 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .18 19 习题2.6.4图 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .18 20 习题2.7.1图 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .19 21 习题2.7.2图 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .20 22 习题2.7.5图 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .20 23 习题2.7.7图 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .21 24 习题2.7.8图 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .22 25 习题2.7.9图 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .23 26 习题2.7.10图 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .23 27 习题2.7.11图 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .24222.12.1.1电路的分析方法电阻串并联接的等效变换在图1所示的电路中 ,E=6V ,R1=6,R2=3,R3=4,R4=3,R5=1,试求I3 和I4 . [解 ] 解图 1: 习题2.1.1图本题通过电阻的串联和并联可化为单回路电路计算 .R1 和R4 并联而后与R3 串联,得出的等效电阻R1,3,4 和R2 并联,最后与电源及R5 组成单回路电路, 于是得出电源中电流 I=E R2 (R3 + R1 R4 ) R1 + R4 R5 + R1 R4 ) R2 + (R3 + R1 + R4 6==2A 6×3 3 × (4 + )6+3 1+ 6×3 ) 3 + (4 + 6+3而后应用分流公式得出I3 和I4 I3=2 × 2A=A 6×3 R1 R4 3 3+4+ R2 + R3 + 6+3 R1 + R4 6 2 4 R1 I3=× A=A I4=R1 + R4 6+3 3 9 R2 I=3 I4 的实际方向与图中的参考方向相反. 32.1.2 有一无源二端电阻网络[图2(a)],通过实验测得:当U=10V 时,I=2A;并已知该电阻网络由四个3的电阻构成,试问这四个电阻是如何连接的? [解 ] 解图 2: 习题2.1.2图按题意,总电阻为 R=U 10==5 I 2四个3电阻的连接方法如图2(b)所示. 2.1.3 在图3中,R1=R2=R3=R4=300,R5=600,试求开关S断开和闭和时a和b之间的等效电阻. [解 ] 解图 3: 习题2.1.3图当开关S断开时,R1 与R3 串联后与R5 并联,R2 与R4 串联后也与R5 并联,故 4有 Rab=R5 //(R1 + R3 )//(R2 + R4 ) 1=1 1 1 + + 600 300 + 300 300 + 300=200 当S闭合时,则有 Rab=[(R1 //R2 ) + (R3 //R4 )]//R5=1 1 + R5 1 R1 R2 R3 R4 + R1 + R2 R3 + R4 1 1 1 + 300 × 300 300 × 300 600 + 300 + 300 300 + 300 ==2002.1.5 [图4(a)]所示是一衰减电路,共有四挡.当输入电压U1=16V 时,试计算各挡输出电压U2 . [解 ] 解 a挡: U2a=U1=16V b挡: 由末级看,先求等效电阻R [见图4(d)和(c)] R=同样可得 R=5 . U1 16 ×5=× 5V=1.6V 45 + 5 50 (45 + 5) × 5.5 275==5 (45 + 5) + 5.5 55.5于是由图4(b)可求U2b ,即 U2b=c挡:由图4(c)可求U2c ,即 U2c=d挡:由图4(d)可求U2d ,即 U2d=0.16 U2c ×5=× 5V=0.016V 45 + 5 50 5 U2b 1.6 ×5=× 5V=0.16V 45 + 5 50图 4: 习题2.1.5图 2.1.6 下图所示电路是由电位器组成的分压电路,电位器的电阻RP=270 ,两边的串联电阻R1=350 ,R2=550 .设输入电压U1=12V ,试求输出电压U2 的变化范围. [解 ] 解当箭头位于RP 最下端时,U2 取最小值 R2 U2min=U1 R1 + R2 + RP 550 × 12 350 + 550 + 270=5.64V=当箭头位于RP 最上端时,U2 取最大值 U2max==R2 + RP U1 R1 + R2 + RP 550 + 270 × 12 350 +550 + 270=8.41V 由此可得U2 的变化范围是:5.64 8.41V . 2.1.7 试用两个6V 的直流电源,两个1k的电阻和一个10k的电位器连接成调压范围为5V +5V 的调压电路. 6[解 ] 解图 5: 习题2.1.7图所联调压电路如图5所示. I=当滑动触头移在a点U=[(10 + 1) × 103 × 1 × 103 6]V=5V 当滑动触头移在b点 U=(1 × 103 ×1 × 103 6)V=5V2.1.8 在图6所示的电路中,RP 1 和RP 2 是同轴电位器,试问当活动触点a,b 移到最左端,最右端和中间位置时,输出电压Uab 各为多少伏? [解] 解 6 (6)=1 × 103 A=1mA (1 + 10 + 1) × 103图 6: 习题2.1.8图同轴电位器的两个电位器RP 1 和RP 2 的活动触点固定在同一转轴上,转动转轴时两个活动触点同时左移或右移.当活动触点a,b在最左端时,a点接电源正极,b点接负极,故Uab=E=+6V ;当活动触点在最右端时,a 点接电源负极,b点接正极,故Uab=E=6V ;当两个活动触点在中间位置时,a,b两点电位相等,故Uab=0. 72.32.3.1电源的两种模型及其等效变换在图7中,求各理想电流源的端电压,功率及各电阻上消耗的功率. [解 ] 解图 7: 习题2.3.1图设流过电阻R1 的电流为I3 I3=I2 I1=(2 1)A=1A (1) 理想电流源1 U1=R1 I3=20 × 1V=20V P1=U1 I1=20 × 1W=20W 因为电流从2 PR1=R1 I3=20 × 12 W=20W(取用)(发出)(4) 电阻R22 PR2=R2 I2=10 × 22 W=40W校验功率平衡: 80W=20W + 20W + 40W 8图 8: 习题2.3.2图 2.3.2 计算图8(a)中的电流I3 . [解 ] 解计算本题应用电压源与电流源等效变换最为方便,变换后的电路如图8(b)所示.由此得I=I3=2.3.4 计算图9中的电压U5 . [解 ] 解 2+1 3 A=A=1.2A 1 + 0.5 + 1 2.5 1.2 A=0.6A 2 图 9: 习题2.3.4图 R1,2,3=R1 + R2 R3 6×4=(0.6 + )=3 R2 + R3 6+4 将U1 和R1,2,3 与U4 和R4 都化为电流源,如图9(a)所示. 9 将图9(a)化简为图9(b)所示.其中 IS=IS1 + IS2=(5 + 10)A=15A R0=R1,2,3 R4 3 3 × 0.2==R1,2,3 + R4 3 + 0.2 16I5U53 R0 45=IS=16 × 15A=A 3 R0 + R5 19 +1 16 45=R5 I5=1 × V=2.37V 192.42.4.1支路电流法图10是两台发电机并联运行的电路.已知E1=230V ,R01=0.5 ,E2=226V ,R02=0.3 ,负载电阻RL=5.5 ,试分别用支路电流法和结点电压法求各支路电流. [解 ] 解图 10: 习题2.4.1图10(1) 用支路电流法 I1 + I2=IL E1=R01 I1 + RL IL E2=R02 I2 + RL IL 将已知数代入并解之,得 I1=20A, I2=20A, IL=40A (2) 用结点电压法 E1 E2 230 226 + + R01 R02 0.5 0.3 V=220V=1 1 1 1 1 1 + + + + R01 R02 RL 0.5 0.3 5.5 E1 U 230 220=A=20A R01 0.5 E2 U 226 220=A=20A R02 0.3 220 U=A=40A RL 5.5 U=I1=I2=IL=2.4.2试用支路电流法和结点电压法求图11所示电路中的各支路电流 , 并求三个电源的输出功率和负载电阻RL 取用的功率 . 两个电压源的内阻分别为0.8 和0.4 . [解 ] 解图 11: 习题2.4.2图 (1) 用支路电流法计算本题中有四个支路电流,其中一个是已知的,故列出三个方程即可,即 120 0.8I1 + 0.4I2 116=0 120 0.8I1 4I=0 11 I1 + I2 + 10 I=0 解之,得 I1 I2=9.38A=8.75AI=28.13A (2) 用结点电压法计算120 116 + + 10 0.4 V=112.5V Uab=0.8 1 1 1 + + 0.8 0.4 4 而后按各支路电流的参考方向应用有源电路的欧姆定律可求得 I1=I2 120 112.5 A=9.38A 0.8 116 112.5=A=8.75A 0.4 112.5 Uab=A=28.13A RL 4I=(3) 计算功率三个电源的输出功率分别为P1=112.5 × 9.38W=1055W P2=112.5 × 8.75W=984W P3=112.5 ×10W=1125W P1 + P2 + P3=(1055 + 984 + 1125)W=3164W 负载电阻RL 取用的功率为 P=112.5 × 28.13W=3164W 两者平衡.2.52.5.1结点电压法试用结点电压法求图12所示电路中的各支路电流. [解 ] 解 12图 12: 习题2.5.1图UO O=Ia=Ib=Ic=25 100 25 + + 50 50 50 V=50V 1 1 1 + + 50 50 50 25 50 A=0.5A 50 100 50 A=1A 50 25 50 A=0.5A 50Ia 和Ic 的实际方向与图中的参考方向相反. 2.5.2 用结点电压法计算图13所示电路中A点的电位. [解 ] 解图 13: 习题2.5.2图 1350 50 + 5 V=14.3V VA=10 1 1 1 + + 50 5 202.5.3 电路如图14(a)所示,试用结点电压法求电阻RL 上的电压U ,并计算理想电流源的功率. [解 ] 解图 14: 习题2.5.3图将与4A理想电流源串联的电阻除去(短接)和与16V 理想电压源并联的8电阻除去(断开),并不影响电阻RL 上的电压U ,这样简化后的电路如图14(b)所示,由此得 4+ U=16 4V=12.8V 1 1 1 + + 4 4 8 计算理想电流源的功率时,不能除去4电阻,其上电压U4=4 × 4V=16V ,并由此可得理想电流源上电压US=U4 + U=(16 +12.8)V=28.8V .理想电流源的功率则为 PS=28.8 × 4W=115.2W (发出功率)2.62.6.1叠加定理在图15中 ,(1)当将开关S合在a点时 , 求电流I1 ,I2 和I3 ;(2)当将开关S合在b点时,利用(1)的结果,用叠加定理计算电流I1 ,I2 和I3 . [解 ] 解 14图 15: 习题2.6.1图 (1) 当将开关S合在a点时,应用结点电压法计算: 130 120 + 2 2 V=100V U=1 1 1 + + 2 2 4 130 100 I1=A=15A 2 120 100 I2=A=10A 2 100 A=25A I3=4 (2) 当将开关S合在b点时,应用叠加原理计算.在图15(b)中是20V 电源单独作用时的电路,其中各电流为 I1=I2=4 × 6A=4A 2+4 20 A=6A 2×4 2+ 2+4 2 × 6A=2A 2+4I3=130V 和120V 两个电源共同作用(20V 电源除去)时的各电流即为(1)中的电流,于是得出 I1=(15 4)A=11A I2=(10 + 6)A=16A I3=(25 + 2)A=27A 2.6.2 电路如图16(a)所示,E=12V ,R1=R2=R3=R4 ,Uab=10V .若将理想 15 电压源除去后[图16(b)],试问这时Uab 等于多少? [解 ] 解图 16: 习题2.6.2图将图16(a)分为图16(b)和图16(c)两个叠加的电路,则应有 Uab=Uab + Uab 因 Uab=故 Uab=(10 3)V=7V 2.6.3 应用叠加原理计算图17(a)所示电路中各支路的电流和各元件(电源和电阻) 两端的电压,并说明功率平衡关系. [解 ] 解 (1) 求各支路电流电压源单独作用时[图17(b)]I2=I4=I3=E 10=A=2A R2 + R4 1+4 R3 1 E=× 12V=3V R1 + R2 + R3 + R4 4E 10=A=2A R3 5IE=I2 + I3=(2 + 2)A=4A 16图 17: 习题2.6.3图电流源单独作用时[图17(c)] I2=I4=R4 4 IS=×10A=8A R2 + R4 1+4 1 R2 IS=× 10A=2A R2 + R4 1+4IE=I2=8A I3=0 两者叠加,得 I2=I2 I2=(2 8)A=6A I3=I3 + I3=(2 + 0)A=2A I4=I4 + I4=(2 + 2)A=4A IE=IE IE=(4 8)A=4A 可见,电流源是电源,电压源是负载. (2) 求各元件两端的电压和功率电流源电压 US=R1 IS + R4 I4=(2 × 10 +4 × 4)V=36V 各电阻元件上电压可应用欧姆定律求得电流源功率 PS=USIS=36 × 10W=360W 电压源功率 PE=EIE=10 × 4W=40W 电阻R1 功率 PR1=电阻R2 功率 PR2=2 R1 IS 2 R2 I2 2(发出) (损耗) (损耗)(取用)=2 × 10 W=200W=1 × 62 W=36W 173 电阻R3 功率 PR3=R3 I3=5 × 22 W=20W 2 电阻R4 功率 PR4=R4 I4=4 ×42 W=64W(损耗) (损耗)两者平衡. 2.6.4 图18所示的是R 2RT 形网络,用于电子技术的数模转换中,试用叠加原理证明输出端的电流I为 I=[解 ] 解 UR (23 + 22 + 21 + 20 ) 3R × 24 图 18: 习题2.6.4图图 19: 习题2.6.4图本题应用叠加原理,电阻串并联等效变换及分流公式进行计算求证.任何一个电源UR 起作用,其他三个短路时,都可化为图19所示的电路.四个电源从右到左依次分别单独作用时在输出端分别得出电流: UR UR UR UR , , , 3R × 2 3R × 4 3R × 8 3R × 16 所以 I=UR UR UR UR + + + 3R ×21 3R × 22 3R × 23 3R × 24 UR=(23 + 22 + 21 + 20 ) 4 3R × 2 182.72.7.1戴维南定理与诺顿定理应用戴维宁定理计算图20(a)中1电阻中的电流. [解 ] 解图 20: 习题2.7.1图将与10A理想电流源串联的2电阻除去( 短接 ) , 该支路中的电流仍为10A;将与10V 理想电压源并联的5电阻除去(断开),该两端的电压仍为10V .因此,除去这两个电阻后不会影响1电阻中的电流I,但电路可得到简化[图20(b)],计算方便. 应用戴维宁定理对图20(b)的电路求等效电源的电动势(即开路电压U0 )和内阻R0 . 由图20(c)得U0=(4 × 10 10)V=30V 由图20(d)得 R0=4 所以1电阻中的电流 I=2.7.2 应用戴维宁定理计算图21中2电阻中的电流I. [解 ] 解 19 U0 30=A=6A R0 + 1 4+1 图 21: 习题2.7.2图求开路电压Uab0 和等效电阻R0 .由此得12 6 Uab0=Uac + Ucd + Udb=(1 × 2 + 0 + 6 + 3 × )V=6V 3+6 3×6 R0=(1 + 1 + )=4 3+6 I=6 A=1A 2+42.7.5 用戴维宁定理计算图22(a)所示电路中的电流I. [解 ] 解图 22: 习题2.7.5图 (1) 用戴维宁定理将图22(a)化为等效电源,如图22(b)所示. 20(2) 由图22(c)计算等效电源的电动势E,即开路电压U0 U0=E=(20 150 + 120)V=10V(3) 由图22(d)计算等效电源的内阻R0 R0=0 (4) 由图22(b)计算电流II=2.7.7 在图23中,(1)试求电流I;(2)计算理想电压源和理想电流源的功率,并说明是取用的还是发出的功率. [解 ] 解 E 10=A=1A R0 + 10 10 图 23: 习题2.7.7图 (1) 应用戴维宁定理计算电流I Uab0=(3 × 55)V=10V R0=3 10 I=A=2A 2+3 (2) 理想电压源的电流和功率 5 IE=I4I=( 2)A=0.75A 4 IE 的实际方向与图中相反,流入电压源的2.7.8 电路如图24(a)所示,试计算电阻RL 上的电流IL ;(1)用戴维宁定理;(2)用诺顿定理. [解 ] 解图 24: 习题2.7.8图 (1) 应用戴维宁定理求IL E=Uab0=U R3 I=(32 8 ×2)V=16V R0=R3=8 IL=(2) 应用诺顿定理求IL IS=IabS=IL=2.7.9 电路如图25(a)所示,当R=4时,I=2A.求当R=9时,I等于多少? [解 ] 解把电路ab以左部分等效为一个电压源,如图25(b)所示,则得 I=R0 由图25(c)求出,即 R0=R2 //R4=1 所以 E=(R0 + R)I=(1 + 4) × 2V=10V 当R=9时 I=10 A=1A 1+9 22 E R0 + R U 32 I=( 2)A=2A R3 8 E 16=A=0.5A RL + R0 24 + 8R0 8 × 2A=0.5A IS=RL + R0 24 + 8图 25: 习题2.7.9图 2.7.10 试求图26所示电路中的电流I. [解 ] 解图 26: 习题2.7.10图用戴维宁定理计算. (1) 求ab间的开路电压U0 a点电位Va 可用结点电压法计算 24 48 + 6 V=8V Va=6 1 1 1 + + 6 6 6 b点电位 12 24 + 3 V=2V Vb=2 1 1 1 + + 2 6 3 U0=E=Va Vb=[8 (2)]V=10V (2) 求ab间开路后其间的等效内阻R0 将电压源短路后可见,右边三个6电阻并联,左边2,6,3三个电阻 23也并联,而后两者串联,即得1 1 k=(2 + 1)k=3k R0=+ 1 1 1 1 1 1 + + + + 6 6 6 2 63 (3) 求电流I I=2.7.11 两个相同的有源二端网络N 和N 联结如图27(a)所示,测得U1=4V .若联结如图27(b)所示,则测得I1=1A.试求联结如图27(c)所示时电流I1 为多少? [解 ] 解 10 U0=A=2 × 103 A=2mA 3 R0 + R (3 + 2) × 10图 27: 习题2.7.11图有源二端网络可用等效电源代替,先求出等效电源的电动势E和内阻R0 (1) 由图27(a)可知,有源二端网络相当于开路,于是得开路电压 E=U0=4V (2) 由图27(b)可知,有源二端网络相当于短路,于是得短路电流I1=IS=1A 由开路电压和短路电流可求出等效电源的内阻 R0=(3) 于是,由图27(c)可求得电流I1 I1=4 A=0.8A 4+1 4 E==4 IS 12425111。

电工学（电子技术）习题答案第二部分第六版秦曾煌主编17.3典型例题.例17.1 一个负反馈放大电路其开环放大倍数A=1000,若要求电路的非线性失真从开.环状态的10％减小到闭环状态吼的1％，试计算该电路的负反馈系数F及闭环放大倍数.AF。

解：由于引入负反馈可使非线性失真减小1+AF倍，因此根据题意有.1?9, 则?F???0.009 ...10%1?*****...AF?A1?AF...?1000?1001?1000?0.009例17.2Rb1电路如例17.2图所示，试用瞬时极性法判断电路中级间反馈的极性。

+VccRc1Rc2C2UoUiC1T1Rf1*****2T2Ui+_A1R2R3_+A2Rf2UoRe1R1R e1Ce2R1Ce1_+Uf(a)(b)例17.2图解：正、负反馈的判断可用瞬时极性法。

反馈的结果使净输入量减小的反馈为负反馈，使净输入量增大的反馈为正反馈。

在图（a）所示电路中，电阻Rf1引入级间交、直反馈；由于C2的隔直作用，Rf2引入交流反馈。

在T1的基极加一对“地”的瞬时极性为正的信号，并标上“?”，第一级为一”共射组态，输出与输入反相，故T1的集电极信号电压对“地”的瞬时极性为负，并标上“○。

第二级也为共射组态，故T2集电极信号瞬时极性为“?”，一”瞬时极性为“○。

Ue2与Ub2同相，即发射极由于UUe2一”为“○，经电阻RRf1一”馈送至T1管发射极的信号瞬时极性也为“○，使T1管b、e间的净输入信号增加，故由于为“?”，经电阻Rf2f1引入的级间反馈为正反馈。

c2馈送至T1管发射极的信号瞬时极性也为“?”，使T1f2管b、e 间的净输入信号减弱，故R引入的级间反馈为负反馈。

在图（b）所示电路中，电阻R2引入级间交直流反馈。

运算放大器电路反馈极性的判断同样可采用瞬时极性法。

运放通常有两个输入端，即反相输入端U?和同相输入端U。

前者和输出U0相位相反，后者和输出U0相位相同。

第一章习题1－1 指出图1－1所示电路中A 、B 、C 三点的电位。

图1－1 题 1－1 的电路解：图（a ）中，电流 mAI 51226.=+=, 各点电位 V C = 0V B = 2×1.5 = 3V V A = (2+2)×1.5 = 6V图（b ）中，电流mAI 1246=+=， 各点电位 V B = 0V A = 4×1 = 4VV C =－ 2×1 = －2V图（c ）中，因S 断开，电流I = 0， 各点电位 V A = 6V V B = 6VV C = 0 图（d ）中，电流mAI 24212=+=， 各点电位 V A = 2×(4+2) =12VV B = 2×2 = 4V V C = 0图（e ）的电路按一般电路画法如图，电流mAI 12466=++=，各点电位 V A = E 1 = 6VV B = (－1×4)+6 = 2V V C = －6V1－2 图1－2所示电路元件P 产生功率为10W ，则电流I 应为多少? 解：由图1－2可知电压U 和电流I 参考方向不一致，P = －10W ＝UI 因为U ＝10V , 所以电流I ＝－1A图 1－2 题 1－2 的电路1－3 额定值为1W 、10Ω的电阻器，使用时通过电流的限额是多少？ 解：根据功率P = I 2 R A R P I 3160101.===1－4 在图1－3所示三个电路中，已知电珠EL 的额定值都是6V 、50mA ，试问哪个电珠能正常发光？图 1－3 题 1－4 的电路解：图（a ）电路，恒压源输出的12V 电压加在电珠EL 两端，其值超过电珠额定值，不能正常发光。

图（b ）电路电珠的电阻Ω=Ω==120120506K R .，其值与120Ω电阻相同，因此电珠EL 的电压为6V ，可以正常工作。

图（c ）电路，电珠与120Ω电阻并联后，电阻为60Ω，再与120Ω电阻串联，电珠两端的电压为V4126012060＝＋⨯小于额定值，电珠不能正常发光。