苏教版数学高一对数函数名师导学案

2019-2020学年高中数学 第三章《对数函数》第三课时导学案苏教版必修1【学习目标】（1）进一步理解对数函数的图象和性质；（2）熟练应用对数函数的图象和性质，解决一些综合问题；（3）通过例题和练习的讲解与演练，培养学生分析问题和解决问题的能力． 【学习重点】对数函数的图像与性质的综合运用。

【预习内容】对数函数的图像与性质。

【新知应用】例1、 求函数)78lg()(2-+-=x x x f 的定义域及值域．变式训练：（1）已知)13(log -a a 恒为正数，求a 的取值范围．（2）函数x y a log =在[2，4]上的最大值比最小值大1，求a 的值；（3）求函数)106(log 23++=x x y 的最小值．例2、已知x 满足20.50.52(log )7log 30x x ++≤ ，求函数22()(log )(log )24x x f x =的最值。

变式训练：已知)91(log 2)(3≤≤+=x x x f ，求函数[])()(22x f x f y +=的最大值和最小值。

例3、已知函数)1lg()(2++=x x x f（1） 求)(x f 的定义域；（2）求)(x f 的奇偶性；（3）判定)(x f 的单调性；（4）求)(x f 的值域。

【新知回顾】本节课主要是在学习对数函数图像与性质的基础之上进行简单的综合应用，同时对于含参问题要能进行正确地分析。

对数函数（3）作业1．函数x x f 3log )(=在区间],[b a 上的值域为]1,0[,则a b -的最小值为2. 函数2lg(2)y x x =-的定义域是 ,值域是 ，单调增区间是3.判断下列函数的奇偶性：)1ln()(2x x x f -+=4.（1）证明函数)1(log )(22+=x x f 在),0(+∞上是增函数。

（2）探究：函数)1(log )(22+=x x f 在)0,(-∞上是减函数还是增函数？5.求函数2lg lg )(2++=x x x f 在[]100,1内的最值。

【教学目标】1. 了解对数函数的概念及表示方法。

2. 掌握对数函数的图像特征、单调性、奇偶性等基本特征。

3. 学会进行对数函数的平移、伸缩和翻折等基本变形。

4. 理解对数函数在实际问题中的应用。

【教学重点】1. 掌握对数函数的图像特征、单调性、奇偶性等基本特征。

2. 学会进行对数函数的平移、伸缩和翻折等基本变形。

【教学难点】1. 学会进行对数函数的平移、伸缩和翻折等基本变形。

【教学过程】Step 1 导入（5分钟）通过举例让学生了解什么是对数，并引出对数函数的定义及表示方法。

Step 2 对数函数的定义及基本特征（10分钟）1. 对数函数的定义：对数函数是以一个正实数 a（a>0且a≠1）作为底数的函数。

loga x = y，则a的y次方等于x，可表示为a^y = x。

2. 对数函数的基本特征：（1）定义域：(0,+∞)，值域R。

（2）单调性：当a>1时，函数图像是单调递增的；当0<a时，函数图像是单调递减的。

（3）奇偶性：对数函数是奇函数，即f(-x)=-f(x)。

（4）渐近线：横轴是对数函数的水平渐近线。

Step 3 对数函数的图像特征（10分钟）1. a > 1 时，对数函数的图像是一条开口向右上方的单调递增的曲线。

2. 01 时，对数函数的图像是一条开口向右下方的单调递减的曲线。

3. 渐近线：横轴是对数函数的水平渐近线。

Step 4 对数函数的平移、伸缩和翻折等基本变形（20分钟）1. 平移：y=loga(x-h)+k2. 伸缩：（1）横向伸缩：y=loga(bx)（2）纵向伸缩：y=cloga(x)3. 翻折：y=-loga(1/x)Step 5 对数函数在实际问题中的应用（10分钟）通过举例让学生了解对数函数在实际问题中的应用，如pH值、声音强度等。

Step 6 练习（10分钟）练习对数函数的图像变形。

Step 7 总结（5分钟）总结本节课所学内容，重点难点，并解答疑惑。

宿迁中学高一数学(必修1) 课题：对数函数（一） 导学案班级_______学号________姓名________组内评价_____【三维目标】1. 知识与技能① 理解指数函数与对数函数之间的联系与区别。

② 理解对数函数的概念，能熟练的进行比较大小。

2. 过程与方法① 通过师生之间，学生与学生之间的合作交流，使学生学会与别人共同学习。

② 通过探究对数函数的概念，感受化归思想，培养学生数学的分析问题的意识。

3. 情感态度价值观① 通过对对数函数概念的学习，使学生认清基本概念的来龙去脉，加深对人类认识事物的一般规律的理解和认识，使学生体会知识之间的有机联系，感受数学的整体性，激发学生的学习兴趣。

② 通过学生的相互交流来加深理解对数函数概念，增强学生数学交流能力，培养学生倾听，接受别人建议的优良品质。

【教学重难点】1. 对数函数和指数函数之间的联系；2. 理解对数函数的概念，体会对数函数是一类重要的函数模型；3. 掌握对数函数的图像和性质，会求与对数函数有关的复合函数的定义域和值域【教具准备】多媒体课件，投影仪，打印好的作业。

【教学过程】一. 预习填空:1.一般地，把函数 叫做对数函数，其中 是自变量，函数的定义域是 ，值域 .（可从指数式和对数式的互化来理解）3.指数函数y=a x (a>0且a ≠1)和对数函数y = log a x (a>0且a ≠1)是关于 对称二、例题讲解例1.求下列函数的定义域(1).0.2log (4);y x =- (2).log 0,1)ay a a =>≠(3). 61log 13y x =- (4). 2lg(23)y x x =+-变式训练：①.求函数1log (164)x x y +=-的定义域②.已知函数2log ()a y a a =-,其中a>1，求它的定义域和值域例2.比较下列各组数中两个值的大小23.4log 3.82①.log 与 0.50.5②.log 1.8与log 2.1 65l o g 77③.log 与变式训练：比较大小36①.log 5与log 5 1.9 2.1②.(lgm)与(lgm)（m>1）三.巩固练习1.函数的定义域2.若log 2log 20a b <<，则a ，b 与0，1的大小关系3.若函数()y f x =的图像与函数ln y x =的图像关于直线y x =对称，则()f x =4.函数2log (6)y x =- (2)x ≥-的值域为5.设20.30.3,2,2a b c ===，则a ，b ，c 的大小关系6.对数函数图像过点P （8，3），则1()2f =7.函数1()log a f x x -=在其定义域上是减函数，则a 的取值范围8.3lg 40x +=四．总结：①本节课学习的知识点有：②本节课所用的思想方法有：五：课堂作业: 课本P70 习题2.3(2) 2 , 3 P69 练习4作业 对数函数(1)1. 已知函数()f x =M ，()ln(1)g x x =+的定义域为N ，则M N = 2. 若0<x<1,则0.2x 2log x （填>或<）3.函数2()lg(31)f x x =++的定义域是 4. 若函数(4)x y f =的定义域为[0,1],则函数2(log )y f x =的定义域为5. 若log (21)log (4)0a a a a +<<，则a 的取值范围是6．已知函数2()log (2)f x x =-的值域是[1,4]，那么函数()f x 的定义域是7.（2009全国卷Ⅱ文）设2lg ,(lg ),a e b e c ===a ，b ，c 的大小关系：8.对于函数2()lg(21)f x ax x =++.①若()f x 的定义域为R ，则a 的取值范围②若()f x 的值域为R ，则a 的取值范围9. 解下列不等式33log (4)2log x x ->+①. .2log (4)log (2)a a x x ->-②10. 对于函数124()lg 3x x a f x ++=. ①若()f x 在(,1)-∞上有意义，求a 的取值范围； ②若()f x 的定义域为(,1)-∞，求a 的值探究●拓展 ：已知函数222()log 3,[1,4],()()[()]f x x x g x f x f x =+∈=-，求：①函数()f x 的值域②()g x 的最大值以及相应的x 的值。

2019-2020学年高中数学 第三章《对数函数 对数》第一课时导学案苏教版必修1【学习目标】1.了解对数式的由来和含义，清楚对数式中各字母的取值范围及与指数式之间的关系．能认识到指数与对数运算之间的互逆关系，并根据概念进行指数与对数之间的互化。

2.会利用指数式的运算推导对数运算性质和法则，能用符号语言和文字语言描述对数运算法则，并能利用运算性质完成简单的对数运算．3.能运用旧知识去探索新知并渗透化归的思想，培养学生的逻辑思维能力．4.通过法则探究，激发学生学习的积极性，增强学生学习的兴趣以及培养大胆探索，实事求是的科学精神．【学习重点】对数的概念和对数的运算性质。

【预习内容】1．定义：若b a N =（__________），则b =__________．2．两个对数：⑴常用对数：_______； ⑵ 自然对数：__________．3．四条恒等式：⑴1的对数是______，即_____________；⑵底数的对数是______，即________________； ⑶=b a a log __________； ⑷=N a a log __________。

4、求值（1）log 636= _______（2）81log 2=_______（3）811log 27=_______ 【新知学习】一、复习旧知、引出新课问题1: 对于xa N =,回答(1)若已知a=4,x=3,求N.(2)若已知N=4,x=-2,求a.(3)若已知a=4,N=64,求x.思考:(1)和(2)是什么运算,如果没有给定具体的数值能否求出相应的值?并试着通过举出更多的例子来探索一下对于(3)一般的问题应该如何求解.问题2： 对数的定义是什么？指数式与对数式的关系是什么？二、给出概念、巩固新知对数的定义：【新知深化】问题3: (1)根据之前对指数的学习,回答为什么定义中要求a ＞0，a ≠1.(2)根据定义,指数与对数之间存在什么关系?(3)定义中各字母的取值范围.问题4： (1)是不是所有的实数都有对数？?1log )2(=a ?log )3(=a a三、例题讲解例1将下列指数式化为对数式162)1(4=；2713)2(3=-；205)3(=a ；45.0)21)(4(=b例2对数式化为指数式3125log )1(5=；23log )2(31-=；699.1log )3(10-=a两种对数：常用对数：我们通常将以10为底的对数叫做常用对数为了简便,N 的常用对数N 10log 简记作lgN 例如：5log 10简记作lg5 ; 5.3log 10简记作lg3.5.自然对数：在科学技术中常常使用以无理数e=2.71828……为底的对数，以e 为底的对数叫自然对数，为了简便，N 的自然对数N e log 简记作lnN 例如：3log e 简记作ln3 ; 10log e 简记作ln10例３求下列各式的值 ①12log 1= ；②ln e = ③2log 256= ； ④lg 0.01= ；⑤3log 81= ⑥64log 2=________⑦27log 9=____________【新知回顾】1.对数的定义： b N a =log ，a 叫做对数的底数，N 叫做真数。

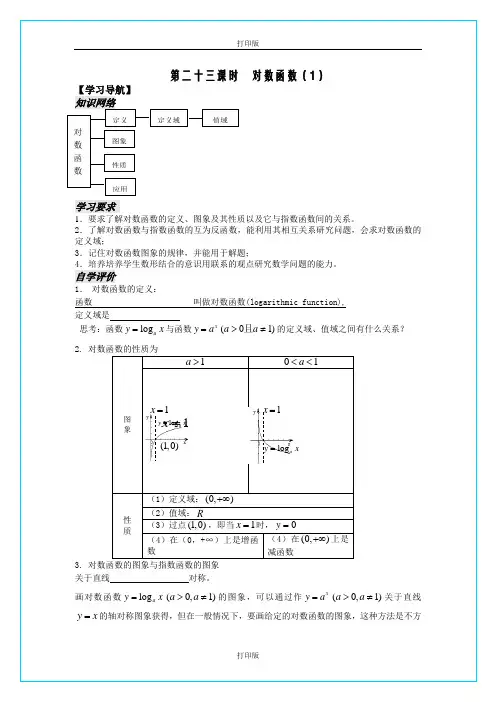
第二十三课时 对数函数（1）
【学习导航】
知识网络
学习要求
1．要求了解对数函数的定义、图象及其性质以及它与指数函数间的关系。

2．了解对数函数与指数函数的互为反函数，能利用其相互关系研究问题，会求对数函数的定义域；
3．记住对数函数图象的规律，并能用于解题；
4．培养培养学生数形结合的意识用联系的观点研究数学问题的能力。

自学评价
1． 对数函数的定义：
函数 叫做对数函数(logarithmic function),
定义域是
思考：函数log a y x =与函数x y a =)10(≠>a a 且的定义域、值域之间有什么关系？
2. 对数函数的性质为
图 象
1a >
01a <<
性
质 （1）定义域：(0,)+∞ （2）值域：R （3）过点(1,0)，即当1=x 时，0=y
（4）在（0，+∞）上是增函
数 （4）在(0,)+∞上是减函数
3. 对数函数的图象与指数函数的图象
关于直线 对称。

画对数函数log a y x =(0,1)a a >≠的图象，可以通过作x y a =(0,1)a a >≠关于直线
y x =的轴对称图象获得，但在一般情况下，要画给定的对数函数的图象，这种方法是不方
数 图象
性质
值域 定义域 定义 应用 对
函 数 (1,0)1x =1x =log a y x =log a y x = 1x =。

高中数学 对数函数（1）学案 苏教版必修1学习目标：1．理解对数函数的概念，能正确描绘对数函数的图象；2．掌握对数函数的性质，并能初步应用对数的性质解决简单问题。

学习重点：对数函数的定义、图象和性质；对数函数性质的初步应用。

学习难点：底数a 对对数函数性质的影响。

学习过程： 一、预习导学1.一般地，函数()log 0,1a y x a a =>≠叫做 ，其中x 叫做 ，函数的定义域是 。

2.对数函数的性质为图 象 1a > 01a <<性 质（1）定义域： （2）值域： （3）过点 （4）在（0，+∞）上是单调 函数 （4）在(0,)+∞上是单调 函数3.指数函数xy a =(0,1)a a >≠与 称为互为反函数。

指数函数的定义域和值域分别是对数函数的 和 。

它们的图象关于直线 对称。

二、课堂研习例1：利用对数函数的性质，比较大小。

（1）2log 3.4，2log 3.8；（2）7log 5，6log 7；（3）2log 1.1，2log 2.1（4）2log 3，4log 5，32例2：求下列函数的定义域（1）0.2log (4)y x =-； （2）2(21)log (23)x y x x -=-++； （3）2log (43)y x =-例3：解不等式（1）55log (3)log (21)x x <+； （2）()()()2log 4log 20,1a a x x a a ->->≠1x =1x =log ay x=log a y x =1x =对数函数（1）作业1.下列函数中是对数函数的是（其中1,0≠>a a ） 。

①)1(log +=x y a ②x y a 2log = ③x y a log 2= ④x y alog =2. 设x y lg =，则下列结论中错误 。

①1=x 时，0=y ； ②1>x 时，0>y ； ③100<<x 时，10<<y ； ④10=x 时，1=y3. 比较下列各题中两个值的大小： ①0.8log 1.5 0.8log 2；②ln 2 ln 2.7；③3log 7 5log 3；4 .设323log ,log log a b c π=== 按从小到大的顺序排列是 5. 函数f(x)= )1(log 1|2|2---x x 的定义域为6. 若函数()2xy f =的定义域为[]1,0-，则函数()2log y f x =的定义域为 。