纯剪切切应力互等定理剪切胡克定律

材料力学（一)轴向拉伸与压缩【内容提要】材料力学主要研究构件在外力作用下的变形、受力与破坏、失效的规律。

为设计既安全可靠又经济合理的构件,提供有关强度、刚度与稳定性分析的基本理论与方法。

【重点、难点】重点考察基本概念，掌握截面法求轴力、作轴力图的方法，截面上应力的计算。

【内容讲解】一、基本概念强度—-构件在外力作用下，抵抗破坏的能力，以保证在规定的使用条件下,不会发生意外的断裂或显著塑性变形.刚度-—构件在外力作用下，抵抗变形的能力，以保证在规定的使用条件下不会产生过分的变形。

稳定性--构件在外力作用下，保持原有平衡形式的能力，以保证在规定的使用条件下,不会产生失稳现象。

杆件——一个方向的尺寸远大于其它两个方向的尺寸的构件，称为杆件或简称杆。

根据轴线与横截面的特征，杆件可分为直杆与曲杆，等截面杆与变截面杆。

二、材料力学的基本假设工程实际中的构件所用的材料多种多样，为便于理论分析，根据它们的主要性质对其作如下假设。

(一）连续性假设-—假设在构件所占有的空间内均毫无空隙地充满了物质，即认为是密实的。

这样，构件内的一些几何量，力学量(如应力、位移）均可用坐标的连续函数表示,并可采用无限小的数学分析方法。

（二)均匀性假设——很设材料的力学性能与其在构件中的位置无关。

按此假设通过试样所测得的材料性能，可用于构件内的任何部位（包括单元体).(三)各向同性假设——沿各个方向均具有相同力学性能。

具有该性质的材料，称为各向同性材料。

综上所述，在材料力学中,一般将实际材料构件，看作是连续、均匀和各向同性的可变形固体。

三、外力内力与截面法（一）外力对于所研究的对象来说,其它构件和物体作用于其上的力均为外力，例如载荷与约束力.外力可分为:表面力与体积力;分布力与集中力；静载荷与动载荷等.当构件（杆件)承受一般载荷作用时，可将载荷向三个坐标平面（三个平面均通过杆的轴线，其中两个平面为形心主惯性平面）内分解，使之变为两个平面载荷和一个扭转力偶作用情况.在小变形的情况下，三个坐标平面内的力互相独立，即一个坐标平面的载荷只引起这一坐标平面内的内力分量,而不会引起另一坐标平面内的内力分量。

一、概述在力学中，胡克定律是描述弹性物体受力变形规律的基本定律之一。

它广泛应用于工程材料力学、结构设计和材料科学等领域。

胡克定律最常见的表达式是描述拉伸和压缩时的定律，即单向拉压。

然而，在一些特定情况下，物体可能同时受到拉力和压力，或者受到剪切力的作用。

本文将探讨单向拉压和纯剪切时胡克定律的表达式，旨在深入理解胡克定律在不同受力情况下的应用。

二、单向拉压时的胡克定律表达式1. 拉伸时的胡克定律表达式在拉伸情况下，弹性体的长度会发生变化，拉力会导致物体变形。

根据胡克定律，拉伸应力与拉伸应变之间存上线性关系，表达式如下：σ = Eε其中，σ表示拉伸应力，单位为帕斯卡（Pa）；E表示弹性模量，单位为帕斯卡（Pa）；ε表示拉伸应变，无量纲。

这个关系表明，对于弹性材料来说，拉伸应力与拉伸应变成正比，且比例系数为弹性模量。

2. 压缩时的胡克定律表达式在压缩情况下，弹性体的体积会发生变化，压力会导致物体变形。

根据胡克定律，压缩应力与压缩应变之间同样存上线性关系，表达式如下：σ = -Eε其中，σ表示压缩应力，单位为帕斯卡（Pa）；E表示弹性模量，单位为帕斯卡（Pa）；ε表示压缩应变，无量纲。

这个关系表明，对于弹性材料来说，压缩应力与压缩应变也呈线性关系，且比例系数同样为弹性模量。

三、纯剪切时的胡克定律表达式在纯剪切情况下，物体受到的是平行但大小相等的剪切力，从而导致物体的形状变化。

在这种情况下，胡克定律的表达式可以表示为：τ = Gγ其中，τ表示剪切应力，单位为帕斯卡（Pa）；G表示剪切模量，单位为帕斯卡（Pa）；γ表示剪切应变，无量纲。

这个表达式表明，在纯剪切情况下，剪切应力与剪切应变同样呈线性关系，并且比例系数为剪切模量。

四、结论通过以上讨论，我们可以看出胡克定律在单向拉压和纯剪切情况下的表达式分别为σ = Eε和τ = Gγ。

这些表达式揭示了物体受力时应力和应变之间的线性关系，为工程材料的力学性能和材料设计提供了重要依据。

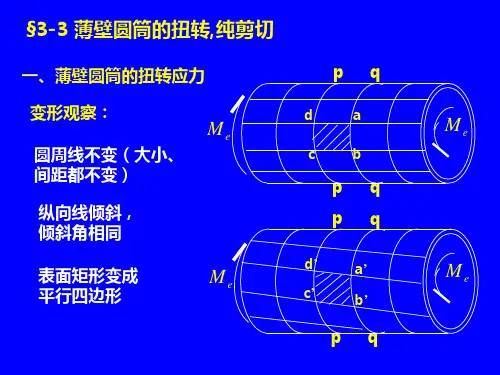
纯剪切① 纵向线倾斜了微小角度 γ；② 各圆周线的形状、大小及间距保持不变，只是绕轴线x 转动了不同的角度。

1.薄壁圆管（平均半径r ≥10δ）的扭转剪切变形：两个截面之间所有小矩形方格的左右两个侧面产生相对错动，矩形变成平行四边形。

l n n m mln n m m切应变：纵向线倾斜的角度 γ（矩形方格变形前后 直角的改变量）。

2. 薄壁圆管扭转时横截面切应力τ 的计算由于管壁很薄，认为切应力沿管壁均匀分布τ τδd φ e d Ar A M τ=⎰ed 2πA r A r r M ττδ==⎰e 22πM r τδ=3. ϕ 与 γ 的关系 d x d yδx y τ τ' z 纯剪切：单元体各截面上只有切应力而无正应力作用，这种应力状态叫做纯剪切应力状态。

4. 纯剪切 l l rγϕ=r l γϕ∴=切应力互等定理切应力互等定理：在相互垂直的两个平面上，切应力必然成对存在，且大小相等。

切应力的方向都垂直于两个平面的交线，且共同指向或共同背离这一交线。

''0y F ττ=→=∑0z M =∑'d d d d 0x y y x τδτδ-='ττ=''''0x F τττ=→==∑d x d y δ x yτ τ'z τ''' τ''剪切胡克定律o γ ττpτs A γτOA 段切应力不超过剪切比例极限 τp 时，切应力τ与切应变γ成正比，即 称为剪切胡克定律。

其中，比例常数G 称为切变模量。

常用单位GPa 。

研究薄壁圆管的扭转实验，得到材料纯剪切条件下的应力与应变关系:G τγ=对各向同性材料，弹性常数E 、G 、μ 存在关系：表明3个常数不是相互独立的。

2(1)E G μ=+。

第3章 扭转1、扭转的概念：杆件的两端个作用一个力偶，其力偶矩大小相等、转向相反且作用平面垂直于杆件轴线，致使杆件的任意两个横截面都发生绕轴线的相对转动，即为扭转变形。

2、外力偶矩的计算{}{}{}min /95491000602r KW m N e e n P M P M n=⇒⨯=⨯⨯⋅π 式中，e M 为外力偶矩。

又由截面法：e e M T M T =⇒=-0 T 称为n n -截面上的扭矩。

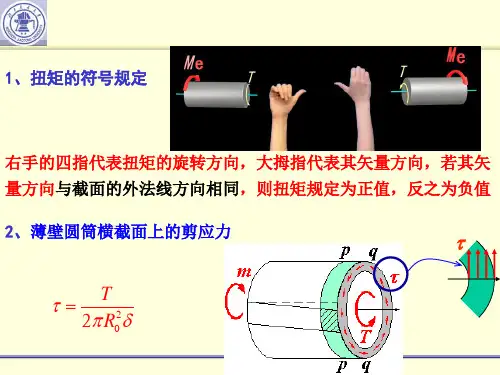
规定：若按右手螺旋法则把T 表示为矢量，当矢量方向与研究部分中截面的外法线的方向一致时，T 为正；反之为负。

3、纯剪切（1）薄壁圆筒扭转时的切应力 δπττδπ222r M r r M ee =⇒••=（2）切应力互等定理：在单元体相互垂直的两个平面上，切应力必然成对存在，且数值相等；两者都垂直于平面的交线，方向则共同指向或背离这一交线。

（3）切应变 剪切胡克定律：当切应力不超过材料的剪切比例极限时，切应变γ与切应力τ成正比。

γτG = G 为比例常数，称为材料的切变模量。

弹性模量E 、泊松比μ和切变模量G 存在关系：)1(2μ+=EG 4、圆轴扭转时的应力（1）变形几何关系：距圆心为ρ处的切应变为dxd ϕργρ=（2）物理关系：ρτ为横截面上距圆心为ρ处的切应力。

dxd G G ϕρτγτρρρ=⇒= （3）静力关系：内力系对圆心的力矩就是横截面的扭矩：dA d d GdA T AxA⎰⎰==2ρρτϕρ 以p I 表示上式右端的积分式：dA I Ap ⎰=2ρ p I 称为横截面对圆心O 点的极惯性矩（截面二次极矩）横截面上距圆心为ρ的任意点的切应力：pI T ρτρ=ρ最大时为R ，得最大切应力：pI TR =max τ引用记号RI W p t =t W 称为抗扭截面系数。

则tW T =max τp I 和t W 的计算（1）实心轴：3224420032D R d d dA I RAp ππθρρρπ====⎰⎰⎰16233D R RI W p t ππ===（2）空心轴：)1(32)(324444202/2/32αππθρρρπ-=-===⎰⎰⎰D d D d d dA I D d Ap)1(16)(164344αππ-=-==D d D DRI W p t5、圆轴扭转时的变形pGI Tl =ϕ ϕ为扭转角，l 为两横截面间的距离。