切应力互等定理
- 格式:pptx
- 大小:98.59 KB
- 文档页数:4



1、应力 全应力正应力切应力线应变 的大小; 外力偶矩当功率P 当功率拉压杆件横截面上只有正应力σ,且为平均分布,其计算公式为 N FAσ= 3-1式中N F 为该横截面的轴力,A 为横截面面积;正负号规定 拉应力为正,压应力为负; 公式3-1的适用条件:1杆端外力的合力作用线与杆轴线重合,即只适于轴向拉压杆件; 2适用于离杆件受力区域稍远处的横截面;3杆件上有孔洞或凹槽时,该处将产生局部应力集中现象,横截面上应力分布很不均匀; 4截面连续变化的直杆,杆件两侧棱边的夹角020α≤时 拉压杆件任意斜截面a 图上的应力为平均分布,其计算公式为全应力 cos p ασα= 3-2正应力 2cos ασσα=3-3切应力1sin 22ατα=3-4 式中σ为横截面上的应力;正负号规定:α 由横截面外法线转至斜截面的外法线,逆时针转向为正,反之为负;ασ 拉应力为正,压应力为负;ατ 对脱离体内一点产生顺时针力矩的ατ为正,反之为负;两点结论:1当00α=时,即横截面上,ασ达到最大值,即()max ασσ=;当α=090时,即纵截面上,ασ=090=0;2当045α=时,即与杆轴成045的斜截面上,ατ达到最大值,即max ()2αατ=1.2 拉压杆的应变和胡克定律 1变形及应变杆件受到轴向拉力时,轴向伸长,横向缩短;受到轴向压力时,轴向缩短,横向伸长;如图3-2;图3-2 轴向变形 1l l l ∆=- 轴向线应变 llε∆= 横向变形 1b b b ∆=- 横向线应变 bbε∆'=正负号规定 伸长为正,缩短为负; 2胡克定律当应力不超过材料的比例极限时,应力与应变成正比;即 E σε= 3-5 或用轴力及杆件的变形量表示为 N F ll EA∆=3-6 式中EA 称为杆件的抗拉压刚度,是表征杆件抵抗拉压弹性变形能力的量;公式3-6的适用条件:a 材料在线弹性范围内工作,即p σσ〈;b 在计算l ∆时,l 长度内其N 、E 、A 均应为常量;如杆件上各段不同,则应分段计算,求其代数和得总变形;即1ni ii i iN l l E A =∆=∑3-7 3泊松比 当应力不超过材料的比例极限时,横向应变与轴向应变之比的绝对值;即 ενε'=3-8强度计算许用应力 材料正常工作容许采用的最高应力,由极限应力除以安全系数求得; 塑性材料 σ=s s n σ ; 脆性材料 σ=b bn σ其中,s b n n 称为安全系数,且大于1;强度条件:构件工作时的最大工作应力不得超过材料的许用应力; 对轴向拉伸压缩杆件[]NAσσ=≤ 3-9 按式1-4可进行强度校核、截面设计、确定许克载荷等三类强度计算; 2.1 切应力互等定理受力构件内任意一点两个相互垂直面上,切应力总是成对产生,它们的大小相等,方向同时垂直指向或者背离两截面交线,且与截面上存在正应力与否无关;2.2纯剪切单元体各侧面上只有切应力而无正应力的受力状态,称为纯剪切应力状态; 2.3切应变切应力作用下,单元体两相互垂直边的直角改变量称为切应变或切应变,用τ表示; 2.4 剪切胡克定律在材料的比例极限范围内,切应力与切应变成正比,即 G τγ= 3-10式中G 为材料的切变模量,为材料的又一弹性常数另两个弹性常数为弹性模量E 及泊松比ν,其数值由实验决定;对各向同性材料,E 、 ν、G 有下列关系 2(1)EG ν=+ 3-112.5.2切应力计算公式横截面上某一点切应力大小为 p pT I ρτ=3-12 式中p I 为该截面对圆心的极惯性矩,ρ为欲求的点至圆心的距离;圆截面周边上的切应力为 max tTW τ=3-13 式中p t I W R=称为扭转截面系数,R 为圆截面半径;2.5.3 切应力公式讨论(1) 切应力公式3-12和式3-13适用于材料在线弹性范围内、小变形时的等圆截面直杆;对小锥度圆截面直杆以及阶梯形圆轴亦可近似应用,其误差在工程允许范围内; (2) 极惯性矩p I 和扭转截面系数t W 是截面几何特征量,计算公式见表3-3;在面积不变情况下,材料离散程度高,其值愈大;反映出轴抵抗扭转破坏和变形的能力愈强;因此,设计空心轴比实心轴更为合理;2.5.4强度条件圆轴扭转时,全轴中最大切应力不得超过材料允许极限值,否则将发生破坏;因此,强度条件为[]max maxt T W ττ⎛⎫=≤⎪⎝⎭ 3-14 对等圆截面直杆 []maxmax tT W ττ=≤ 3-15式中[]τ为材料的许用切应力; 3.1.1中性层的曲率与弯矩的关系1zMEI ρ=3-16 式中,ρ是变形后梁轴线的曲率半径;E 是材料的弹性模量;E I 是横截面对中性轴Z 轴的惯性矩; 3.1.2横截面上各点弯曲正应力计算公式 ZMy I σ=3-17 式中,M 是横截面上的弯矩;Z I 的意义同上;y 是欲求正应力的点到中性轴的距离最大正应力出现在距中性轴最远点处 max max max max z zM My I W σ=•= 3-18 式中,max z z I W y =称为抗弯截面系数;对于h b ⨯的矩形截面,216z W bh =;对于直径为D 的圆形截面,332z W D π=;对于内外径之比为d a D =的环形截面,34(1)32z W D a π=-; 若中性轴是横截面的对称轴,则最大拉应力与最大压应力数值相等,若不是对称轴,则最大拉应力与最大压应力数值不相等;3.2梁的正应力强度条件梁的最大工作应力不得超过材料的容许应力,其表达式为 []maxmax zM W σσ=≤ 3-19 对于由拉、压强度不等的材料制成的上下不对称截面梁如T 字形截面、上下不等边的工字形截面等,其强度条件应表达为[]maxmax 1l t z M y I σσ=≤ 3-20a []maxmax 2y c zM y I σσ=≤ 3-20b 式中,[][],t c σσ分别是材料的容许拉应力和容许压应力;12,y y 分别是最大拉应力点和最大压应力点距中性轴的距离;3.3梁的切应力 z z QS I bτ*= 3-21式中,Q 是横截面上的剪力;z S *是距中性轴为y 的横线与外边界所围面积对中性轴的静矩;z I 是整个横截面对中性轴的惯性矩;b 是距中性轴为y 处的横截面宽度; 3.3.1矩形截面梁切应力方向与剪力平行,大小沿截面宽度不变,沿高度呈抛物线分布;切应力计算公式 22364Q h y bh τ⎛⎫=- ⎪⎝⎭3-22最大切应力发生在中性轴各点处,max 32QAτ=; 3.3.2工字形截面梁切应力主要发生在腹板部分,其合力占总剪力的95~97%,因此截面上的剪力主要由腹板部分来承担;切应力沿腹板高度的分布亦为二次曲线;计算公式为 ()2222824z Q B b h H h y I b τ⎡⎤⎛⎫=-+-⎢⎥ ⎪⎝⎭⎣⎦3-23近似计算腹板上的最大切应力:dhFs 1max=τd 为腹板宽度 h 1为上下两翼缘内侧距3.3.3圆形截面梁横截面上同一高度各点的切应力汇交于一点,其竖直分量沿截面宽度相等,沿高度呈抛物线变化;最大切应力发生在中性轴上,其大小为 2max42483364z z d d Q QS Q d I b Adππτπ*⋅⋅===⨯ 3-25 圆环形截面上的切应力分布与圆截面类似;3.4切应力强度条件梁的最大工作切应力不得超过材料的许用切应力,即 []max max maxz z Q S I bττ*=≤ 3-26式中,max Q 是梁上的最大切应力值;max z S *是中性轴一侧面积对中性轴的静矩;z I 是横截面对中性轴的惯性矩;b 是maxτ处截面的宽度;对于等宽度截面,max τ发生在中性轴上,对于宽度变化的截面,max τ不一定发生在中性轴上; 4.2剪切的实用计算名义切应力:假设切应力沿剪切面是均匀分布的 ,则名义切应力为 AQ=τ 3-27 剪切强度条件:剪切面上的工作切应力不得超过材料的 许用切应力[]τ,即 []ττ≤=AQ3-285.2挤压的实用计算名义挤压应力 假设挤压应力在名义挤压面上是均匀分布的,则 []bsbs bs bsP A σσ=≤ 3-29 式中,bs A 表示有效挤压面积,即挤压面面积在垂直于挤压力作用线平面上的投影;当挤压面为平面时为接触面面积,当挤压面为曲面时为设计承压接触面面积在挤压力垂直面上的 投影面积;挤压强度条件挤压面上的工作挤压应力不得超过材料的许用挤压应力 []bs bsbs A Pσσ≤=3-30 1, 变形计算圆轴扭转时,任意两个横截面绕轴线相对转动而产生相对扭转角;相距为l 的两个横截面的相对扭转角为dx GI TlP⎰=0ϕ rad 4.4 若等截面圆轴两截面之间的扭矩为常数,则上式化为PGI Tl=ϕ rad 4.5 图4.2式中P GI 称为圆轴的抗扭刚度;显然,ϕ的正负号与扭矩正负号相同;公式4.4的适用条件:(1) 材料在线弹性范围内的等截面圆轴,即P ττ≤;(2) 在长度l 内,T 、G 、P I 均为常量;当以上参数沿轴线分段变化时,则应分段计算扭转角,然后求代数和得总扭转角;即 ∑==ni P i ii iI G l T 1ϕ rad 4.6 当T 、P I 沿轴线连续变化时,用式4.4计算ϕ; 2, 刚度条件扭转的刚度条件 圆轴最大的单位长度扭转角max 'ϕ不得超过许可的单位长度扭转角[]'ϕ,即[]''maxmax ϕϕ≤=PGI T rad/m 4.7 式 []'180'max max ϕπϕ≤⨯=︒P GI T m /︒ 4.82,挠曲线的近似微分方程及其积分在分析纯弯曲梁的正应力时,得到弯矩与曲率的关系EIM=ρ1对于跨度远大于截面高度的梁,略去剪力对弯曲变形的影响,由上式可得()()EIx M x =ρ1 利用平面曲线的曲率公式,并忽略高阶微量,得挠曲线的近似微分方程,即 ()EIx M =''ω 4.9 将上式积分一次得转角方程为 ()C dx EIx M +==⎰'ωθ 4.10再积分得挠曲线方程 ()D Cx dx dx EI x M ++⎥⎦⎤⎢⎣⎡=⎰⎰ω 4.11 式中,C,D 为积分常数,它们可由梁的边界条件确定;当梁分为若干段积分时,积分常数的确定除需利用边界条件外,还需要利用连续条件; 3,梁的刚度条件限制梁的最大挠度与最大转角不超过规定的许可数值,就得到梁的刚度条件,即 []ωω≤max ,[]θθ≤max 4.12 3,轴向拉伸或压缩杆件的应变能在线弹性范围内,由功能原理得 l F W V ∆==21ε 当杆件的横截面面积A 、轴力F N 为常量时,由胡克定律EAlF l N =∆,可得 EA l F V N 22=ε 4.14杆单位体积内的应变能称为应变能密度,用εV 表示;线弹性范围内,得 σεε21=V 4.15 4,圆截面直杆扭转应变能 在线弹性范围内,由功能原 ϕe r M W V 21== 将T M e =与P GI Tl =ϕ代入上式得 Pr GI lT V 22= 4.16图4.5根据微体内的应变能在数值上等于微体上的内力功,得应变能的密度r V : r V r τ21= 4.175,梁的弯曲应变能在线弹性范围内,纯弯曲时,由功能原理得 将M M e =与EIMl=θ代入上式得 EI l M V 22=ε 4.18图4.6横力弯曲时,梁横截面上的弯矩沿轴线变化,此时,对于微段梁应用式4.18,积分得全梁的弯曲应变能εV ,即()⎰=lEI dxx M V 22ε 4.192.截面几何性质的定义式列表于下:静 矩 惯性矩惯性半径惯性积 极惯性矩3.惯性矩的平行移轴公式静矩:平面图形面积对某坐标轴的一次矩,如图Ⅰ-1所示; 定义式: ⎰=Ay zdA S ,⎰=Az ydA S Ⅰ-1量纲为长度的三次方;由于均质薄板的重心与平面图形的形心有相同的坐标C z 和C y ;则由此可得薄板重心的坐标 C z 为 AS A zdA z yAC==⎰同理有 A S y zC =所以形心坐标 A S z y C =,ASy z C = Ⅰ-2或 C y z A S ⋅=,C z y A S ⋅=由式Ⅰ-2得知,若某坐标轴通过形心轴,则图形对该轴的静矩等于零,即0=C y ,0=z S ;0=C z ,则 0=y S ;反之,若图形对某一轴的静矩等于零,则该轴必然通过图形的形心;静矩与所选坐标轴有关,其值可能为正,负或零;如一个平面图形是由几个简单平面图形组成,称为组合平面图形;设第 I 块分图形的面积为 i A ,形心坐标为Ci Ci z y , ,则其静矩和形心坐标分别为 Ci i n i z y A S 1=∑=,Ci i ni y z A S 1=∑= Ⅰ-3∑∑====ni ini Cii z C AyA AS y 11,∑∑====ni ini cii y C AzA AS z 11 Ⅰ-4§Ⅰ-2 惯性矩和惯性半径惯性矩:平面图形对某坐标轴的二次矩,如图Ⅰ-4所示;⎰=Ay dA z I 2,⎰=Az dA y I 2 Ⅰ-5量纲为长度的四次方,恒为正;相应定义AI i y y =,AI i zz =Ⅰ-6 为图形对 y 轴和对 z 轴的惯性半径;组合图形的惯性矩;设 zi yi I I , 为分图形的惯性矩,则总图形对同一轴惯性矩为yi ni y I I 1=∑=,zi ni z I I 1=∑= Ⅰ-7若以ρ表示微面积dA 到坐标原点O 的距离,则定义图形对坐标原点O 的极惯性矩⎰=Ap dA I 2ρ Ⅰ-8因为 222z y +=ρ所以极惯性矩与轴惯性矩有关系 ()z y Ap I I dA z yI +=+=⎰22Ⅰ-9式Ⅰ-9表明,图形对任意两个互相垂直轴的轴惯性矩之和,等于它对该两轴交点的极惯性矩;下式 ⎰=Ayz yzdA I Ⅰ-10定义为图形对一对正交轴 y 、z 轴的惯性积;量纲是长度的四次方; yz I 可能为正,为负或为零;若 y ,z 轴中有一根为对称轴则其惯性积为零;§Ⅰ-3平行移轴公式由于同一平面图形对于相互平行的两对直角坐标轴的惯性矩或惯性积并不相同,如果其中一对轴是图形的形心轴()c cz ,y时,如图Ⅰ-7所示,可得到如下平行移轴公式⎪⎩⎪⎨⎧+=+=+=abA II A b I I Aa I I C C C C z y yzz z y y 22 Ⅰ-13 简单证明之: 其中⎰AC dA z 为图形对形心轴 C y 的静矩,其值应等于零,则得同理可证I-13中的其它两式;结论:同一平面内对所有相互平行的坐标轴的惯性矩,对形心轴的最小;在使用惯性积移轴公式时应注意 a ,b 的正负号;把斜截面上的总应力p 分解成与斜截面垂直的正应力n σ和相切的切应力n τ图222123n l m n σσσσ=++ 2222222123n n l m n τσσσσ=++-在以n σ为横坐标、n τ截面上的正应力n σ和切应力n τ区域图13.2中阴影中的一点;由图13.2显见。

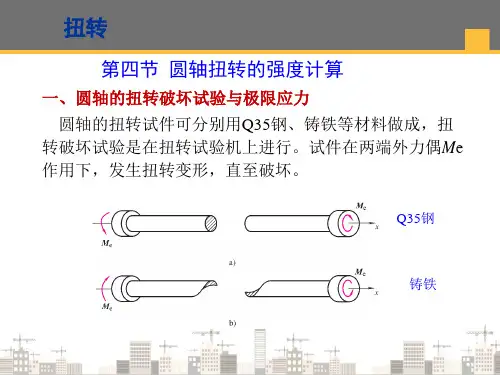
扭转切应力两类切应力扭转切应力弯曲切应力扭转切应力圆轴扭转时的应力变形特征圆轴扭转时横截面上的切应力分析矩形截面杆扭转切应力公式圆轴扭转时的应力变形特征外加力偶矩与功率和转速的关系变形特征横截面和纵截面都有切应力存在--切应力互等定理外加力偶矩与功率和转速的关系应用此公式时要注意单位。
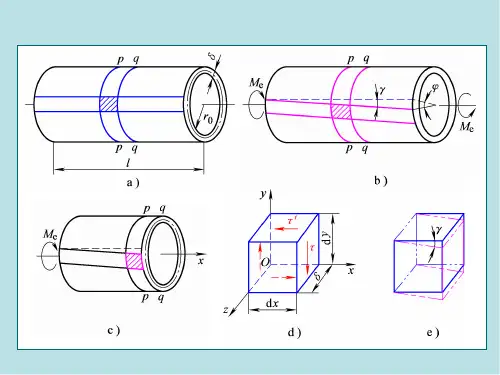
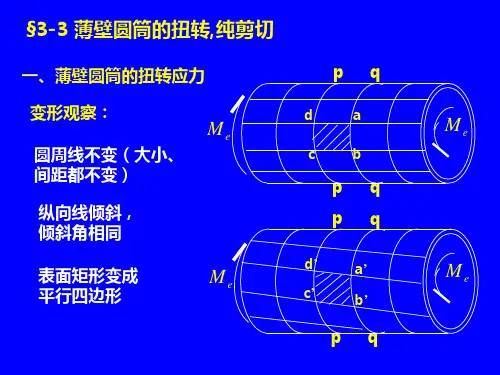
将圆轴表面如图划分为许多小方块,这些小方块可近似地看作矩形。
轴受扭以后,小方块就发生变形,变成菱形。
如图是放大后的情形。
产生这样的变形是因为在两个横截面上出现了切应力。
作用在AB、CD面上的切应力组成一个力偶,显然它是不能使这个微元平衡的,因此,在两个纵截面上也产生切应力。
通过应变知道横截面上有切应力,再通过平衡知道纵截面上也有切应力。
微元的直角改?横截面上和纵截面上的切应力有何关系?我们取出如图微元分析,横截面上的切应力τ乘以其作用面积dydz,再乘以力臂dx,组成一个力偶;纵截面上的切应力τ'也同样组成一个力偶,这两个力偶是大小相等,方向相反的。
最后消掉公因子dxdydz,就得到τ=τ'。
根据平衡的要求?圆轴扭转时横截面上的切应力根据变形特征和切应力互等定理,现在分析圆轴扭转时横截面上的切应力。
反对称分析论证平面保持平面由平面保持平面导出变形协调方程由物性关系得到应力分布切应力公式方法与过程反对称分析论证平面保持平面首先用反对称关系。
如图,对称圆轴两端作用一对反对称的力偶,横截面上C、D两点若不保持在原来的平面上,则从A端看,力偶是顺时针方向的,这两点背离观察者而去的;若从B端看,力偶也是顺时针方向的,C、D两点也背离观察者而去。
显然这是矛盾的,因此,C、D两点只能?第一个结论圆轴扭转时,横截面保持平面,平面上各点只能在平面内转动还可以用反对称关系作进一步分析这些平面上的点移动的规律。
观察截面上的一条直径,若发生扭曲,当分别从A、B两端看过去时,一次呈S形,一次呈反S形,同样产生矛盾的结论。
最终结论圆轴扭转时,横截面保持平面,并且只能发生刚性转动。


切应力互等定理的推导1. 引言切应力互等定理是固体力学中的一个重要定理,用于描述材料的切变变形与应力之间的关系。
它是基于切变应力和应变之间的线性关系推导出来的。
本文将对切应力互等定理的推导过程进行详细阐述。
2. 切变应力和应变的定义首先,我们需要明确切变应力和应变的定义。
在固体力学中,切变应力是指单位面积上的切向力,通常用符号τ表示。
而应变是指物体在受力作用下产生的形变程度,通常用符号γ表示。
3. 切应力互等定理的表达式切应力互等定理的表达式可以写作:τ = Gγ其中,τ表示切变应力,G表示剪切模量,γ表示应变。
切应力互等定理表明,在弹性范围内,切变应力和应变之间存在线性关系,且比例系数为剪切模量。
4. 推导过程为了推导出切应力互等定理,我们需要从基本原理出发,利用一些假设和已知条件,进行推导。
4.1 假设在推导过程中,我们需要做出以下假设: - 材料是均匀各向同性的; - 材料在弹性范围内变形,不发生塑性变形; - 材料的应力和应变是线性关系。
4.2 应变的定义根据应变的定义,我们可以将应变表示为位移的导数。
对于切变应变,它是由切变位移引起的,因此可以表示为:γ = du/dy其中,du表示位移的微小变化,dy表示与du相对应的微小切向位移。
4.3 应力的分析在推导过程中,我们需要对材料受力进行分析。
考虑一个矩形的微小体积元素,其边长分别为dx、dy和dz。
根据平衡条件,我们可以得到切向应力的表达式:τ = (σx - σx+dx)/dy其中,σx表示x方向上的应力。
4.4 应力的线性关系根据假设,材料的应力和应变是线性关系。
因此,我们可以将应力表示为应变的线性函数:σx = Eεx其中,σx表示x方向上的应力,E表示杨氏模量,εx表示x方向上的应变。
4.5 应变的微分形式将应变的定义代入应力的线性关系中,我们可以得到应变的微分形式:du/dy = (εx - εx+dx)/dy4.6 切应力的表达式将应力的线性关系和应变的微分形式代入切应力的表达式中,我们可以得到切应力的表达式:τ = (σx - σx+dx)/dy = (Eεx - E(εx+dx))/dy = E(εx - εx+dx)/dy4.7 切应力互等定理的推导根据切应力的表达式,我们可以得到切应力和应变之间的关系:τ = E(εx - εx+dx)/dy考虑到应变的定义,我们可以将其改写为:τ = E(du/dy - (du+dx)/dy)= E(du - du+dx)/dy= E(du - d(du+dx))/dy= E(du - ddu - dx)/dy= E(du - ddu)/dy - E(dx)/dy= E(du/dy - d(du/dy)) - E(dx/dy)根据微积分的基本知识,我们可以将上式化简为:τ = E(d²u/dy²) - E(dx/dy)最后,我们可以将切应力互等定理的表达式写作:τ = Gγ其中,G = E/dy表示剪切模量。

切应力互等定理概念切应力互等定理(Reciprocal theorem of shear stress)是固体力学中的一个重要概念,它描述了在弹性体中产生切应力时的相互关系。
本文将详细介绍切应力互等定理的概念、原理和应用。
1.概念切应力互等定理是指在一个弹性体内,两个相互作用的切应力具有互等的特性。
简而言之,如果一个切应力的分量在某一平面上施加于弹性体,则该平面上的相对切应力分量将会产生一个与之等大但方向相反的切应力。
2.原理切应力互等定理的原理基于弹性体的线性行为和能量守恒的原则。
根据弹性体的线性弹性理论,应力和应变之间存在线性关系。
而根据能量守恒原理,外力所做的功等于应变能的增量。
根据这两个原理,可以推导出切应力互等定理。
考虑一个弹性体,在其内部选择两个非共面的点A和B,并通过这两个点作一个平行于一块面的剪切力。
根据切应力互等定理,当在A点施加一个单位的切应力时,会在B点上产生相等但方向相反的切应力。
3.数学表达数学上,切应力互等定理可以通过向量和张量的形式进行表述。
设在平面x-y 上有一个剪切应力τxy作用于弹性体上,根据切应力互等定理,位于平面y-z上的剪切应力τyz将与τxy大小相等但方向相反。
对于一个三维弹性体,切应力互等定理可以表示为:τij=τji其中,τij表示位于平面i-j上的切应力分量,而τji表示位于平面j-i上的切应力分量。
4.应用切应力互等定理在固体力学中具有广泛的应用,尤其在结构力学、材料力学和地震工程等领域。
-结构力学:在结构设计中,切应力互等定理可用于计算和分析各种复杂结构的切应力分布和变形情况。
通过使用切应力互等定理,可以简化计算和分析过程,并提高结构设计的效率。
-材料力学:在材料的强度和韧性分析中,切应力互等定理可以用于推导材料的应变能密度和破坏准则。
通过将切应力互等定理与其他弹性常数和材料参数相结合,可以得到更准确的材料性能评估。
-地震工程:在地震工程中,切应力互等定理可以用于模拟和分析地震时产生的地表切应力分布。

切应力互等定理是固体力学中的重要概念,用于描述材料在受到切应力时的行为。
在适当的条件下,切应力互等定理可以帮助我们更好地理解材料的力学性质,并为工程设计和实际应用提供指导。
本文将就切应力互等定理的适用条件进行详细阐述,以便读者更好地理解这一概念。
1. 切应力互等定理的基本概念切应力互等定理是指在材料受到切应力时,材料内部不同方向上的切应力大小相等。
也就是说,如果材料在某一方向上受到一定大小的切应力,那么在与该方向垂直的另一方向上也会受到相同大小的切应力。
这一定理的提出,得益于对于材料内部微观结构的研究,通过将微观层面的知识与宏观力学行为进行通联,得出了这一定理。
2. 切应力互等定理的适用条件切应力互等定理在一定的条件下才能成立,主要的适用条件包括以下几点:2.1 材料是各向同性的各向同性是指材料的性质在各个方向上都是均匀的,不存在各向异性。
在各向同性的材料中,切应力在不同方向上的传播规律是一致的,所以切应力互等定理才能成立。
而在各向异性材料中,不同方向上的切应力传播规律会有所不同,因此切应力互等定理就不适用。
2.2 材料呈线弹性线弹性是指在应力未超出一定范围内,应变与应力成正比。
对于线弹性材料,切应力互等定理成立,因为各个方向上的切应变与切应力成正比。
而对于非线弹性材料,由于应力与应变的关系不再是简单的线性关系,在切应力传播过程中会出现一些非线性效应,因此切应力互等定理也不再适用。
3. 切应力互等定理的意义和应用切应力互等定理不仅在理论研究中有着重要的意义,也在工程设计和实际应用中具有指导作用。
通过切应力互等定理,我们可以更好地理解材料在受到切应力时的行为特点,从而为材料的设计和选择提供依据。
在工程实践中,切应力互等定理也可以用于分析材料的疲劳性能和断裂行为,为工程结构的可靠性评估提供支持。
4. 结语切应力互等定理在固体力学中具有着重要的地位,但要想正确理解和应用这一定理,就需要充分了解其适用条件。
切应力互等定理的推导摘要:一、引言二、切应力互等定理的概念与公式三、切应力互等定理的推导过程四、切应力互等定理的应用与意义五、结论正文:一、引言切应力互等定理是固体力学中的一个基本定理,它描述了在任意六面体单元体中,六个面上的切应力之间存在着特定的关系。
本文将从切应力互等定理的概念与公式出发,详细地介绍切应力互等定理的推导过程,以及其在实际应用中的意义。
二、切应力互等定理的概念与公式切应力互等定理指的是,在任意六面体单元体中,六个面上的切应力满足如下关系:任意两个相对面上的切应力大小相等,且它们的方向互相垂直。
用数学公式表示,可以写作:τ1 = τ2, τ1 = -τ3, τ1 = τ4, τ2 = -τ3, τ2 = τ4, τ3 = -τ4其中,τ1、τ2、τ3、τ4 分别表示六面体单元体的六个面上的切应力。
三、切应力互等定理的推导过程为了更好地理解切应力互等定理,我们先来了解一下六面体单元体的概念。
六面体单元体是一个虚拟的六面体,它由六个面组成,每个面代表一个力,这个力可以分解为三个互相垂直的力。
因此,在六面体单元体的每个面上,都有一个正应力和两个切应力。
接下来,我们通过假设和数学推导来证明切应力互等定理。
假设在六面体单元体中,有一个面上的切应力不为零,设为τ。
由于六面体单元体是一个封闭的体系,所以在其他面上必然存在一个与τ大小相等、方向相反的切应力,设为-τ。
根据切应力的平衡条件,这两个切应力在六面体单元体内部必须达到平衡。
因此,在六面体单元体的其他四个面上,必然存在四个切应力,它们的大小相等、方向互相垂直,分别与τ和-τ相平衡。
由此,我们得出了切应力互等定理。
四、切应力互等定理的应用与意义切应力互等定理在实际应用中具有重要意义。
它有助于我们更好地理解应力分布规律,为材料强度计算、结构设计及分析提供理论依据。
此外,切应力互等定理也为实验应力分析提供了依据,通过测量某个面上的切应力,可以推断出其他面上的切应力分布情况。
基本概念:(1)面力、体力与应力、应变、位移的概念及正负号规定(2)切应力互等定理:作用在两个互相垂直的面上,并且垂直于改两面交线的切应力是互等的(大小相等,正负号也相同)。
(3)弹性力学的基本假定:连续性、完全弹性、均匀性、各向同性和小变形。
(4)平面应力与平面应变;设有很薄的等厚度薄板,只在板边上受有平行于板面并且不沿厚度变化的面力或约束。
同时,体力也平行与板面并且不沿厚度方向变化。
这时,二z =0, Z =0,・zy =0,由切应力互等,二Z =0, * =0,・yz =0,这样只剩下平行于xy面的三个平面应力分量,即匚x,二y, xy二yx,所以这种问题称为平面应力问题。
设有很长的柱形体,它的横截面不沿长度变化,在柱面上受有平行于横截面且不沿长度变化的面力或约束,同时,体力也平行于横截面且不沿长度变化,由对称性可知,z^0, z^0,根据切应力互等,任=0,『=0。
由胡克定律,ZX =0, zy =0,又由于z方向的位移w处处为零,即;z = 0。
因此,只剩下平行于xy面的三个应变分量,即;x, ;y, xy,所以这种问题习惯上称为平面应变问题。
(5)一点的应力状态;过一个点所有平面上应力情况的集合,称为一点的应力状态。
(6)圣维南原理;(提边界条件)如果把物体的一小部分边界上的面力,变换为分布不同但静力等效的面力(主失相同,主矩也相同),那么,近处的应力分布将有显著的改变,但是远处所受到的影响可以忽略不计。
(7)轴对称;在空间问题中,如果弹性体的几何形状、约束情况,以及所受的外力作用,都是对称于某一轴(通过该轴的任一平面都是对称面),则所有的应力、变形和位移也就对称于这一轴。
这种问题称为空间轴对称问题。
平衡微分方程:(记:u(记)(1)平面问题的平衡微分方程;(2)平面问题的平衡微分方程(极坐标);——L+ - +—!-- +&P P P CT ptp^2!^ + cP P1、 平衡方程仅反映物体内部的平衡,当应力分量满足平衡方程,则物体内部是 平衡的。
材料力学(应力应变部分)→规定载荷作用下,强度要求,就是指构件应有足够的抵抗破坏的能力。
刚度要求,就是指构件应有足够的抵抗变形的能力。
→变形的基本假设:连续性假设,均匀性假设,各向同性假设。
→沿不同方向力学性能不同的材料,称为各向异性材料,如木材、胶合板和某些人工合成材料。
→ 分布力 表面力集中力(火车轮对钢轨压力,滚珠轴承对轴的反作用力) 体积力是连续分布于物体内各点的力,例如物体的自重和惯性力等。
→动载荷,静载荷→应力p 应分解为正应力σ ,切应力τ 。
→应力单位pa ,1pa=1N/m 2;常用Mpa ,1Mpa=106pa 。
第二章 拉伸、压缩与剪切2.2 轴向拉伸或压缩时横截面上的内力和应力→习惯上,把拉伸的轴力规定为正,压缩时的轴力规定为负。
→用横截面上的应力来度量杆件的受力程度。
→F N =σA ;σ(x)=F N (x)/A(x)2.3 直杆轴向拉伸或压缩时斜截面上的内力和应力 α轴向拉伸(压缩)时,在杆件的横截面上,正应力为最大值;在与杆件轴线成45°的斜截面上,切应力为最大值。
最大切应力在数值上等于最大正应力的二分之一。
此外,α=90°时,σα=τα=0 ,这表示在平行于杆件轴线的纵向截面上无任何应力。
(应力,p=F/A ,45°斜截面上,力→√22,面积→√22。
) 2.7 安全因数许用应力和安全因数的数值,可以在有关部门的一些规范中查到。
目前一般机械制造中,在静载的情况下,对塑性材料可取n s =1.2~2.5。
脆性材料均匀性较差,且断裂突然发生,有更大的危险性,所以取n b =2~3.5,甚至取到3~9。
2.8 轴向拉伸或压缩时的变形→胡克定律,当应力不超过材料的比例极限时,应力与应变成正比。
σ=Eε ,弹性模量E 的值随材料而不同。
∆l l=ε=σE =F AE ;∆l =FLAE即,对长度相同,受力相等的杆件,有EA 越大则变形Δl越小,所以称EA 为杆件的抗拉/压刚度。
第3章 扭转1、扭转的概念:杆件的两端个作用一个力偶,其力偶矩大小相等、转向相反且作用平面垂直于杆件轴线,致使杆件的任意两个横截面都发生绕轴线的相对转动,即为扭转变形。
2、外力偶矩的计算{}{}{}min /95491000602r KW m N e e n P M P M n=⇒⨯=⨯⨯⋅π 式中,e M 为外力偶矩。
又由截面法:e e M T M T =⇒=-0 T 称为n n -截面上的扭矩。
规定:若按右手螺旋法则把T 表示为矢量,当矢量方向与研究部分中截面的外法线的方向一致时,T 为正;反之为负。
3、纯剪切(1)薄壁圆筒扭转时的切应力 δπττδπ222r M r r M ee =⇒••=(2)切应力互等定理:在单元体相互垂直的两个平面上,切应力必然成对存在,且数值相等;两者都垂直于平面的交线,方向则共同指向或背离这一交线。
(3)切应变 剪切胡克定律:当切应力不超过材料的剪切比例极限时,切应变γ与切应力τ成正比。
γτG = G 为比例常数,称为材料的切变模量。
弹性模量E 、泊松比μ和切变模量G 存在关系:)1(2μ+=EG 4、圆轴扭转时的应力(1)变形几何关系:距圆心为ρ处的切应变为dxd ϕργρ=(2)物理关系:ρτ为横截面上距圆心为ρ处的切应力。
dxd G G ϕρτγτρρρ=⇒= (3)静力关系:内力系对圆心的力矩就是横截面的扭矩:dA d d GdA T AxA⎰⎰==2ρρτϕρ 以p I 表示上式右端的积分式:dA I Ap ⎰=2ρ p I 称为横截面对圆心O 点的极惯性矩(截面二次极矩)横截面上距圆心为ρ的任意点的切应力:pI T ρτρ=ρ最大时为R ,得最大切应力:pI TR =max τ引用记号RI W p t =t W 称为抗扭截面系数。
则tW T =max τp I 和t W 的计算(1)实心轴:3224420032D R d d dA I RAp ππθρρρπ====⎰⎰⎰16233D R RI W p t ππ===(2)空心轴:)1(32)(324444202/2/32αππθρρρπ-=-===⎰⎰⎰D d D d d dA I D d Ap)1(16)(164344αππ-=-==D d D DRI W p t5、圆轴扭转时的变形pGI Tl =ϕ ϕ为扭转角,l 为两横截面间的距离。