2019北师大版九年级数学上册第四章相似三角形性质导学案有答案语文

2019-2020学年九年级数学上册 4 图形的相似导学案（新版）北师大版【学习目标】1、学习相似图形，重点研究相似三角形。

2、是学生经历线段比、成比例线段、实力黄金分割，并通过图形相似的具体应用过程，掌握相似图形所应有的方法。

3、通过培养学生对问题的观察、思考、交流、类比、归纳等过程，发展学生的探索精神，合作意识，增强应用数学意识，加深对数学的人文价值的理解和认识。

【学习重点】1、主要概念—线段的比、成比例线段、相似三角形、相似多边形、相似比；2、利用数的比引申到三角形、多边形，进行特殊与一般的某些关系的比较。

【学习难点】灵活应用相似图形的概念解决实际问题。

学习过程： 典型问题分析：例1、设x 3 =y 5 =z 7 ，则x+y y =______，y+3z3y-2z =______.例2、如图，四边形EFGH 是ABC 内接正方形，BC=21cm ，高AD=15cm ，求内接正方形边长EF 。

例3、已知：平行四边形ABCD ，E 是BA 延长线上一点，CE 与AD 、BD 交于G 、F ， 求证：EF GF CF ⋅=2。

例4、如图，四边形ABCD与四边形D EFG都是矩形，顶点F在BA的延长线上，边DG与AF交于点H，AD=4，DH=5，EF=6，求FG的长．例5、如图，△ABC中，AD为∠BAC的平分线，AD的垂直平分线EF交BC的延长线于点F，连接AF．求证：∠B=∠CAF．例6、如图，晚上，小亮走在大街上。

他发现：当他站在大街边的两盏路灯之间，并且自己被两边路灯照在地上的两个影子成一直线时，自己右边的影子长为3米，左边的影子长为1.5米．又知自己身高1.80米，两盏路灯的高相同，两盏路灯之间的距离为12米，求路灯的高。

例7、如图，四边形ABCD中，AC平分∠DAB，∠ADC=∠ACB=90°，E为AB的中点，（1）求证：；（2）求证：CE∥AD；（3）若AD=4，AB=6，求的值．【拓展提升】1、如图，，又，点在同一条直线上。

2019-2020学年九年级数学上册 4.6 利用相似三角形测高导学案（新版）北师大版【学习目标】1、通过测量旗杆的高度的活动，巩固相似三角形有关知识，积累数学活动的经验．2、熟悉测量工具的使用技能，了解小镜子使用的物理原理【学习重难点】重点：综合运用相似三角形判定、性质解决实际问题难点：解决学生在操作过程中如何与课本中有关知识相联系．【学习过程】模块一预习反馈一、知识回顾1、相似三角形：对应角，对应边的三角形叫做相似三角形。

2、相似三角形的性质：对应角，对应边。

3、平行于三角形一边的直线与其它两边相交，截得的对应线段。

二、自主学习1、利用阳光下的影子来测量旗杆的高度原理：同一时刻，某物体的实际高度：某物体的影长=被测物体的实际高度：被测物体的影长。

如图，测得AB=a，BE=b,BD=c，求CD的高度。

2、标杆测量旗杆的高度原理：三点共线如图，测得AB=a，EF=b,BF=c，BD=d求CD的高度。

3、镜子的反射原理：入射角=反射角如图，测得AB=a，BE=b,BD=c，求CD的高度。

模块二合作探究1、小明欲测量一古塔的高度，他站在该塔的影子上前后移动，直到他本身影子的顶端正好与古塔的影子的顶端重叠，此时他距离古塔18m，已知小明的身高是1.6m，他的影长为2m，①△ABC与△ADE是否相似？为什么？②求古塔的高度。

2、如图，九年级（1）班课外活动小组利用标杆测量学校旗杆的高度，已知标杆高度CD=3m，标杆与旗杆的水平距离BD=15m，人的眼睛与地面的高度EF=1.6m，人与标杆CD的水平距离D F=2m，人的眼睛E、标杆顶点C和旗杆顶点A在同一直线，求旗杆AB的高度．模块三、小结反思讲一下你本节课学习了哪些新知识？用到了什么方法或数学思想？1.知识：2.方法：模块四形成提升1、小明为了测量一高楼MN 的高,在离N 点20m 处放了一个平面镜,小明沿NA 后退到C 点，正好从镜子中看到楼顶M ，若AC ＝1.5m,小明的眼睛离地面的高度为1.6m ，请你帮助小明计算一下楼房的高度。

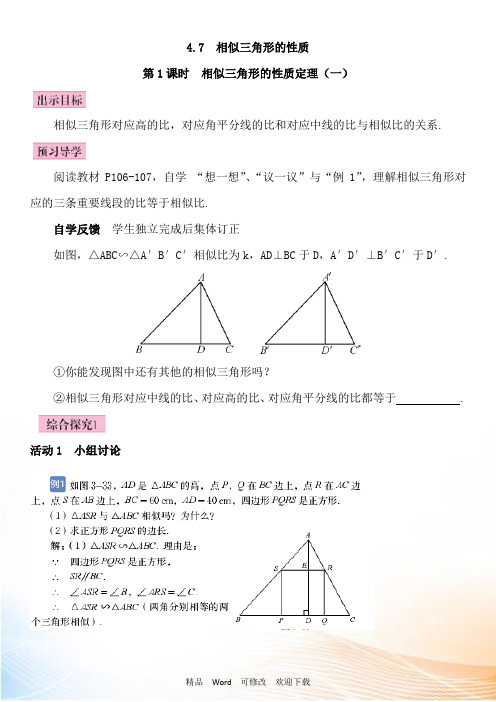
4.7 相似三角形的性质第1课时相似三角形的性质定理（一）相似三角形对应高的比，对应角平分线的比和对应中线的比与相似比的关系.阅读教材P106-107，自学“想一想”、“议一议”与“例1”，理解相似三角形对应的三条重要线段的比等于相似比.自学反馈学生独立完成后集体订正如图，△ABC∽△A′B′C′相似比为k，AD⊥BC于D，A′D′⊥B′C′于D′.①你能发现图中还有其他的相似三角形吗？②相似三角形对应中线的比、对应高的比、对应角平分线的比都等于 .活动1 小组讨论相似三角形的对应高的比、对应角平分线的比和对应中线的比都等于相似比.活动2 跟踪训练(独立完成后展示学习成果)1.如果两个相似三角形对应中线的比为8∶9，则它们的相似比为（）A. 8∶9B.9∶8C.64∶81D.22∶32.已知△ABC∽△DEF，且相似比为2：3，则△ABC与△DEF的对应高之比为（）A．2：3 B．3：2 C．4：9 D．9：43.如图，电灯P在横杆AB的正上方，AB在灯光下的影子为CD AB CD，∥，2mAB=，5mCD=，点P到CD的距离是3m，则点P到AB的距离是（）A．56m B．6m7C．6m5D．10m3AB F CD G E第3题图第4题图4.如图，DE∥BC，则△_______∽△_______.若AD＝3，BD＝2，AF⊥BC，交DE于点G，则AG∶AF＝_______∶_______，△AGE∽△AFC，且它们的相似比为________.5.若C B A ABC '''∆∆∽，且cm AB 2=，cm B A 311=''，则对应角平分线的比为_______. 6.已知C B A ABC '''∆∆∽,对应角平分线的比为22∶，且BC 边上的中线是25，则C B ''边上的中线是_______.7.若△ABC ∽△A ′B ′C ′.AD 、A ′D ′分别是△ABC 、△A ′B ′C ′的高，AD ∶A ′D ′＝3∶4，△A ′B ′C ′的一条中线B ′E ′＝16cm ，则△ABC 的中线BE ＝______ cm. 活动3 课堂小结本节课主要根据相似三角形的性质和判定推导出了相似三角形的性质：相似三角形的对应高的比、对应角平分线的比和对应中线的比都等于相似比.教学至此，敬请使用《名校课堂》相应课时部分.【预习导学】 自学反馈①△ABD ∽△A ′B ′D ′ △ADC ∽△A ′D ′C ′ ②相似比 相似比 【合作探究1】 活动2 跟踪训练1.A2.A3.C4.ADE ，ABC ， 3，5，3∶55.3：26.57.12第2课时 相似三角形的性质定理（二）1.相似三角形的周长比，面积比与相似比的关系.2.相似三角形的周长比，面积比在实际中的应用.阅读教材P109-110，自学，理解相似三角形周长的比等于相似比，面积比等于相似比的平方.自学反馈 学生独立完成后集体订正如图，△ABC ∽△A ′B ′C ′相似比为k ，AD ⊥BC 于D ，A ′D ′⊥B ′C ′于D ′.①你能发现图中还有其他的相似三角形吗？ ②△ABC 与△A ′B ′C ′中，ABC A B C C C '''= ,ABC A B C SS '''= . ③相似三角形周长的比等于 . ④相似三角形面积的比等于 .在运用相似三角形的性质时，要注意周长的比与面积的比之间的区别，不要混为一谈，另外面积的比等于相似比的平方，反过来相似比等于面积比的算术平方根.活动1 小组讨论例1 如图，D 、E 分别是△ABC 的边AB 、AC 的中点，M 是DE 的中点，CM 的延长线交AB 于点N ，则S △DMN ∶S 四边形ANME 的值为多少？解:连接DC.∵点D 、E 分别是AB 、AC 的中点， ∴DE ∥BC.∴△ADE ∽△ABC,△NDM ∽△NBC. ∴DE BC =AD AB =12,ADE ABCSS=(12)2=14,DMN NBCS S=(DM BC )2=(12DEBC)2=(14)2=116.设S △EMC =a,则S △DMC =S △EMC =a ， ∴S △EDC =2S △EMC =2a. 又∵BDC EDCSS=BCDE=2, ∴S △BDC =2S △EDC =4a.∴S 四边形DBCE =S △BDC +S △EDC =4a+2a=6a, S 四边形DBCM =S △BDC +S △DMC =5a. 由ADE ABCS S=14,由NDM NBC S S =116,得x S △ADE =2a ，S △NDM =13a.∴S 四边形ANME =S △ADE -S △DMN =2a-13a=53a. ∴S △DMN ∶S 四边形ANME =13a ∶53a=1∶5.解决本题要注意两个方面的问题:一是先求出小三角形与大三角形面积之间的关系；二是运用代数方法来解较好.活动2 跟踪训练(独立完成后展示学习成果)1.（2021·黔西南州）已知△ABC∽△A′B′C′且，则S△ABC：S△A'B'C′为（）A．1：2 B．2：1 C．1：4 D．4：12.（2021·贵阳）如果两个相似三角形对应边的比为2：3，那么这两个相似三角形面积的比是（）A．2：3 B．： C．4：9 D．8：273.已知，△ABC∽△DEF，△ABC与△DEF的面积之比为1：2，当BC=1，对应边EF的长是（）A． B．2 C．3 D．44.设两个相似多边形的周长比是3：4，它们的面积差为70，那么较小的多边形的面积是（）A．80 B．90 C．100 D．1205.（2021·东莞）若两个相似三角形的周长比为2：3，则它们的面积比是．6.如图，在正方形ABCD中，F是AD的中点，BF与 AC交于点G，则△FGA与△BGC的面积之比是 .7.已知△ABC∽△DEF，，△ABC的周长是12cm，面积是30cm2．（1）求△DEF的周长；（2）求△DEF的面积．活动3 课堂小结学生试述:这节课你学到了些什么？教学至此，敬请使用《名校课堂》相应课时部分.【预习导学】自学反馈①△ABD∽△A′B′D′△ADC∽△A′D′C′②kk2③相似比的平方相似比的平方④相似比【合作探究1】活动2 跟踪训练1.C2.C3.A4.B5. 4：96. 1：47.（1）∵，∴△DEF的周长=（cm）；（2）∵，∴△DEF的面积=（cm2）．。

第2课时两边成比例且夹角相等的两个三角形相似
学习目标：
1、掌握并会推导相似三角形的判定定理2.
2、会用相似三角形的判定定理2进行一些简单的判断、证明和计算.
学习重点：灵活运用相似三角形的判定定理2证明和解决有关问题．
预设难点：相似三角形的判定定理2的推导和应用.
☆预习导航☆
一、链接
1、三角形一边的直线与其他两边（或）相交，截得的三角形与原三角
形 .
2、如果一个三角形的两个角分别与另一个三角形的两个角，那么这两个三角形相似（可简单说成：）.
3、如果一个三角形的两条边分别与另一个三角形的两条边，并且夹角，那么这两个三角形全等（可简单说成：）.
二、导读
结合课本写一写相似三角形的判定定理2的证明过程.
☆合作探究☆
1、如图，在四边形ABCD中，∠A = ∠CBD，AB = 15cm，AD = 20cm，BD = 18cm，BC = 24cm,求CD的长.
2、如图，点C、D在线段AB上，△PCD是等边三角形.
（1）当AC 、CD 、BD 满足什么数量关系时，△ACP ∽△PDB?
（2）当△ACP ∽△PDB 时，求∠APB 的度数.
☆ 归纳反思 ☆
本节课你有哪些收获？还存在哪些困惑？
☆ 达标检测 ☆
1、如图，D 是△ABC 一边BC 上的一点，△ABC ∽△DBA 的条件是( )
A.AC AD BC BD =
B. AC AB BC AD
= C.AB 2＝CD ·BC D.2AB ＝BD ·BC
2、已知：如图，D 是△ABC 边AB 上的一点，且AC 2 =AD ·AB.
求证：∠ADC=∠ACB.。

新北师大版九年级数学上册4.4.探索三角形相似的条件导学案学 习目 标 1.熟练掌握相似三角形的定义； 2.熟练掌握三角形相似的判定方法；3.能灵活运用判定方法判断两个三角形是否相似。

. 重点：掌握相似三角形的判定定理难点：相似三角形判定定理在实际问题中的灵活运用知识链接：【回顾与思考】1．对应角相等，对应边也相等的两个三角形全等，你还记得三角形全等的其他判别条件吗？2．相似三角形的定义是什么？你认为判别两个三角形相似至少需要哪些条件？ 【合作学习】合作1 同学们观察我们的直角三角尺，直观上看它们是什么关系？如果两个三角形有若干个角对应相等，那么至少有几个角对应相等就能保证这两个三角形相似？ 合作2 与同伴合作，两个人分别画△ABC 和△A ′B ′C ′,使得∠A =∠A ′都等于∠α，∠B 和∠B ′都等于∠β，此时，∠C 与∠C ′相等吗？对应边的比C B BCC A AC B A AB '''''',,相等吗？这样的两个三角形相似吗？改变∠α，∠β的大小，再试一试.由此得到相似三角形的判定方法1：【例题学习】如图，D 、E 分别是△ABC 边AB 、AC 上的点，DE ∥B C ，AB =7，AD =5，DE =10，求BC 的长。

备注（教师复备栏及学生笔记）备注（教师复【巩固训练】1、如图D 、E 分别是△ABC 边AB 、AC 上的点，∠AED=∠C ，△ABC 与△ADE 相似吗？如果相似请写出证明过程AB C ED2、已知：如图，∠1=∠2=∠3，求证：△ABC ∽△ADE ．（二） 【知识回顾】 1，如图，12∠=∠，添加一个条件使得ADE ∆∽ACB ∆ . 2，两个三角形有两边成比例，它们一定相似吗？如果增加一角相等，你能说出有哪几种可能的情况吗？ ,【合作学习】1、（1）画△ABC 与△A ′B ′C ′，使∠A =∠A ′，B A AB ''和C A AC''都等于给定的值k .设法比较 ∠B 与∠B ′（或∠C 与∠C ′）的大小，△ABC 与△A ′B ′C ′相似吗？ （2）改变k 值的大小，再试一试.判定方法2： 2.如果△ABC 与△A ’B ’C ’两边成比例，且其中一边所对的角相等，那么这两个三角形一定相似吗？由此你能得到什么结论？ 备栏及学生笔记）备注（教师复备栏及学装订线21ED CB A结论：【例题学习】 例：如图，D ,E 分别是△ABC 的边AC ,AB 上的点，AE =1.5，AC =2，BC =3，且AD AB =34，求DE 的长.AB CE D（三） 【知识回顾】我们已经有哪些判别两三角形相似的方法？ 【合作学习】画△ABC 与△A ′B ′C ′，使B A AB ''、C B BC ''和A C CA''都等于给定的值k . （1）设法比较∠A 与∠A ′的大小； （2）△ABC 与△A ′B ′C ′相似吗？说说你的理由.改变k 值的大小，再试一试.判定方法3：例：如图在△ABC 和△ADE 中，AB AD =BC DE =ACAE ，∠BAD=20°，求∠CAE 的度数.生笔记备注（教师复备栏及学生笔记【巩固练习】1、如图，AB•AE=AD•AC ，且∠1=∠2，求证：△ABC ∽△ADE ．2、依据下列条件，证明△ABC 与△A ′B ′C ′相似.AB =10 cm,BC =8cm,AC=16cm,A ′B ′=16cm,B ′C ′=12.8 cm ，A′C ′=25.6cm ，【拓展运用】如图△ABC 与△ADE 有公共点A ，∠DAB=∠CAE ，试添加一个条件，使△ABC ∽△ADE ，并加以证明.ABCDE【归纳小结】250°) EDF1.650°)4ABC3.2。

第四章图形的相似§4.4探索相似三角形的条件 知识点1.相似三角形判定定理1（1）相似三角形的定义相似三角形的定义:三角对应______，三边对应___________的两个三角形叫相似三角形. 相似三角形的表示方法:△ABC 与△DEF 相似,记作______________.（2）相似三角形判定定理1：____________________对应相等的两个三角形相似.（3）三角形相似常见图形⑴ 已知：DE ∥BC则相似的三角形:______________________________,相等的角:____________________________________,成比例的边:___________________________________.⑵ 已知:∠B=∠AED 则相似的三角形:______________________________,相等的角:____________________________________,成比例的边:___________________________________.⑶ 已知：∠ADC=∠ACB则相似的三角形:______________________________,相等的角:____________________________________,成比例的边:___________________________________.⑷ 已知：AB ∥DE B EB则相似的三角形:______________________________,相等的角:____________________________________,成比例的边:___________________________________.⑸已知:∠B=∠E则相似的三角形:______________________________,相等的角:____________________________________,成比例的边:___________________________________.⑹已知：在Rt△ABC中，∠ACB=90°CD⊥AB于D互余的角:_______________________________相等的角:_____________________________________相似的三角形:_______________________________等积式:_______________________________.典型例题【例1】．如图，有三个三角形，其中相似的是（）A．（1）和（2）B．（2）和（3）C．（1）和（3）D．（1）（2）（3）三个都相似【例2】如图10，口ABCD中，E是边BC上的点，AE交BD于点F，如果BEBC＝23，那么BFDF＝．B D【例3】．如图，E 是▱ABCD 的边CD 延长线上一点，连接BE ，交AC 于点O ，交AD 于F ，则图中的相似三角形（不包括全等）共有（ ）A ．7对B ．6对C ．5对D ．4对【例4】．如图，D 是△ABC 中BC 边上的一点，E 为AD 边上的一点，若∠DAC ＝∠B ，CD ＝CE ．试说明△ACE ∽△BAD ．【例5】．如图，在□ABCD 中，过点A 作AE 丄BC 于点，连接DE ,F 为线段DE 上一点，且∠AFE＝∠B ．(1)求证：△ADF ∽△DEC ；⑵若AB ＝8，AD ＝63，AF ＝43，求AE 的长．D知识点2.相似三角形的判定方法2两边______________且_________________的两个三角形相似【例1】 如图1，要使△ACD ∽△ABC ，需要补充的条件是( )A ．B ．C ．DB AD CD ⋅=2 D ．AB AD AC ⋅=2 【例2】. 如图,等腰三角形ABC 中,AB=AC,D 为CB 延长线上一点,E 为BC 延长线上点,且满足AB 2=DB· CE.求证:△ADB ∽△EAC.BC AB CD AC =AC BC AD CD =【例3】：如图,P为正方形ABCD的边BC上的点,BP=3PC,Q是CD中点,求证:△ADQ∽△QCP.【例4】. 如图，已知△ABC、△DCE、△FEG是三个全等的等腰三角形，底边BC、CE、EG在同一直线上，且AB=，BC=1，连接BF，分别交AC、DC、DE于点P、Q、R．求证：△BFG∽△FEG，并求出BF的长；知识点3.相似三角形的判定方法3_______________________________的两个三角形相似【例1】. 如图，小正方形的边长均为1，则下列图中的三角形(阴影部分)与△ABC 相似的是( )【例2】. 如图，在△ABC 和△ADE 中，AE ACDE BCAD AB==，∠BAD=20°，求∠CAE 的度数.【例3】. 如图，四边形ABCD、CDEF、EFGH都是正方形．（1）求证：△ACF∽△GCA；（2）求∠1+∠2的度数．【例4】已知：如图，AD是△ABC的高，E、F分别是AB、AC的中点．求证：△DFE∽△ABC．综合题【例1】．下列各组三角形中，两个三角形能够相似的是( )A．△ABC中，AB＝8，AC＝4，∠A＝105°，△A'B'C'中，A'B'＝16，B'C＝8，∠A'＝100°B．△ABC中，AB＝18，BC＝20，CA＝35，△A'B'C'中，A'B'＝36，B'C'＝40，CA'＝70C ．△ABC 和△A'B'C'中，有''''AB BC A B B C =，∠C ＝∠C' D ．△ABC 中，∠A ＝42°，∠B ＝118°，△A'B'C'，中，∠A'＝118°，∠B'＝15°【例2】．如图，在△ABC 中，D 、E 分别是边BC 、AB 的中点，AD ，CE 相交于G ．试说明13GE GD CE AD ==【例3】．如图，在△ABC 中，CE ⊥AB 于E ，BF ⊥AC 于F ，试说明：(1)△ABF ∽△ACE ．(2)△AEF ∽△ACB ．【例4】．如图，在△ABC中，CD⊥AB，DE⊥AC，DF⊥BC，垂足分别为D、E、F．(1) CA·CE与CB·CF相等吗？为什么？(2)连接EF，交CD于点O，线段OC、OF、OE、OD成比例吗？【例5】．已知如图，AB⊥DB于点B，CD⊥DB于点D，AB=6，CD=4，BD=14．则在DB上是否存在点P，使得以C、D、P为顶点的三角形与P、B、A为顶点的三角形相似，如果存在求出DP的长，如果不存在，说明理由．【例6】．如图△ABC中，AB=8，AC=6，如果动点D以每秒2个单位长的速度，从点B出发沿BA方向向点A运动，同时点E以每秒1个单位的速度从点A出发沿AC方向向点C运动，设运动时间为t（单位：秒），问t为何值时△ADE与△ABC相似．【例7】．如图，已知直线y＝－12x＋2与x轴交于点A，与y轴交于点B，在x轴上有一点C，使B、O、C三点构成的三角形与△AOB相似，求此时点C的坐标．。

4题图 5题图 北师大版九年级数学上册《图形的相似》导学案相似三角形的性质（第二课时）【学习目标】1.进一步掌握相似三角形的性质定理及其证明方法；2.能运用相似三角形性质定理解决问题；3.通过相似三角形性质定理及应用的学习，培养学生类比思想、归纳思想及特殊到一般的认识规律，拓展学生思维.【知识梳理】1.相似三角形周长的比等于 .2.相似三角形面积的比等于 .3.相似多边形的性质： .【典型例题】 知识点一 相似三角形周长的比等于相似比.1.两个相似三角形的一对对应边长分别是24cm 和12cm ．(1)若它们的周长和是120cm ，则这两个三角形的周长分别为 和 ；(2)若它们的面积差是420cm 2，则这两个三角形的面积分别为 和 ．2.(内蒙古赤峰期末)两个相似三角形面积比是4∶9，其中一个三角形的周长为18，则另一个三角形的周长是( )A ．12B ．12或24C ．27D ．12或27知识点二：相似三角形面积的比等于相似比的平方3. 已知△ABC ∽△DEF,且△ABC 与△DEF 的面积比为9∶4,△ABC 的最短边为4.5 cm,则△DEF 的最短边为( )A 6 cmB 2 cmC 3 cmD 4 cm4.如图,四边形ABCD 为平行四边形,E,F 为CD 边的两个三等分点,连接AF,BE 交于点G,则S △EFG ∶S △BAG 等于( )(A)1∶3 (B)3∶1(C)1∶9 (D)9∶1 5.将△ABC 沿BC 的方向平移得到△DEF,△ABC 与△DEF 重叠部分的面积是△ABC 的面积的一半,已知BC=2,△ABC 平移的距离为 .【巩固训练】1．若△ABC ∽△DEF ，且S △ABC ：S △DEF ＝5：4，则△ABC 与△DEF 的周长比为（ ）A ．5：4B ．4：5C ．2：D ．：2 2.△ABC 中，DE ∥FG ∥BC ，AD ＝DF ＝FB ，则S △ADE :S 四边形DFGE :S 四边形=C B A B CD EF G2题图 5题图 3题图O AD 3S 2S 1S 3图T R N M P C B A 6题图3.在梯形ABCD 中，AD ∥BC ，AC 、BD 交于O 点AD ∶BC ＝3∶7，则AO ∶OC ＝ ， ∶＝ ，∶＝ .4.两个相似三角形面积之差为9cm 2，对应的高线的比是∶，这两个三角形的面积分别是 .5.如图，在△ABC 中，D 、E 分别是AB 、BC 上的点，且DE ∥AC ，若S △BDE ：S △CDE =1：4 则S △BDE ：S △ACD = .6. 如图，已知P 为△ABC 内一点，过P 点分别作直线平行于△ABC 的各边，形成小三角形的面积1S 、2S 、3S ，分别为4、9、49，则△ABC 的面积为 .7. 如图，在梯形ABCD 中，AD ∥BC ，AC 与BD 相交于 点E ，S △ADE ：S △BCE =4：9，求S △ABD ：S △ABC=【拓展延伸】8. 如图，已知点D 、E 分别在△ABC 的边AC 、BC 上，线段BD 与AE 交于点F ，且CD ⋅CA =CE ⋅CB ．（1）求证：∠CAE =∠CBD ；（2）若BE EC =AB AC ，求证：AB ⋅AD =AF ⋅AE ．AOD S ∆BOC S ∆AOD S ∆AOB S ∆23E D BA7题图。