2012版步步高高考数学考前三个月抢分训练25：函数

专题限时集训(二十)[第20讲 分类与整合思想和化归与转化思想](时间：10分钟＋35分钟)2012二轮精品提分必练2012二轮精品提分必练3．已知α∈⎝ ⎛⎭⎪⎫π2，π，sin α＝35，则tan ⎝⎛⎭⎪⎫α＋π4等于( ) A.17B ．7C ．－17D ．－7 4．设0<a <1，函数f (x )＝log a (a 2x －3a x ＋3)，则使f (x )>0的x 的取值范围是( )A ．(－∞，0)B ．(0，＋∞)C ．(log a 2,0)D ．(log a 2，＋∞)2012二轮精品提分必练1．已知M ＝{x |x －a ＝0}，N ＝{x |ax －1＝0}，若M ∩N ＝N ，则实数a 的值为( )A ．1B ．－1C ．1或－1D ．0或1或－12．设a >0，a ≠1，函数f (x )＝log a x 在区间[a,2a ]上的最大值与最小值之差小于1，则a 的取值范围是( )A ．(0,1)∪(1，＋∞)B.⎝ ⎛⎭⎪⎫0，12∪(2，＋∞) C.⎝ ⎛⎭⎪⎫12，1∪(2，＋∞) D ．(1，＋∞)3．设一直角三角形两直角边的长均是区间(0,1)内的随机数，则斜边的长小于34的概率为( )A.9π64B.964C.9π16D.9164．若sin x ＋cos x ＝13，x ∈(0，π)，则sin x －cos x 的值为( ) A ．±173 B ．－173C.13D.1735．如果函数y ＝a sin x ＋b 的最小值是－1，最大值是3，则a －b ＝________.6．已知直线kx －y ＋1＝0与圆C ：x 2＋y 2＝4相交于A ，B 两点，若点M 在圆C 上，且有OM →＝OA →＋OB →(O 为坐标原点)，则实数k ＝________.7.设函数f (x )＝x －2m sin x ＋(2m －1)sin x cos x(m为实数)在(0，π)上为增函数，试求m的取值范围．8．设函数f(x)＝x2－2x＋a ln x.(1)若函数f(x)是定义域上的单调函数，求实数a的取值范围；(2)求函数f(x)的极值点．专题限时集训(二十)【基础演练】1．D 【解析】 当0<a <1时，log a 2<1⇔log a 2<log a a ⇒a <2，故0<a <1；若a >1，则log a 2<1⇔log a 2<log a a ⇒2<a ，故a >2.所以a 的取值范围是(0,1)∪(2，＋∞)．2．B 【解析】 当a >0时，a 2＋2a ≥2a 2·2a＝2； 当a <0时，a 2＋2a ＝－⎣⎢⎡⎦⎥⎤⎝ ⎛⎭⎪⎫－a 2＋⎝ ⎛⎭⎪⎫－2a ≤ －2⎝ ⎛⎭⎪⎫－a 2·⎝ ⎛⎭⎪⎫－2a ＝－2. 3．A 【解析】 由α∈⎝ ⎛⎭⎪⎫π2，π，sin α＝35，可得tan α＝－34，对tan ⎝ ⎛⎭⎪⎫α＋π4进行恒等变形化为1＋tan α1－tan α，把tan α＝－34代入计算得17. 4．C 【解析】 根据对数函数的性质可得不等式0<a 2x －3a x ＋3<1，换元后转化为一元二次不等式求解．令t ＝a x ，则0<t 2－3t ＋3<1，因为Δ＝(－3)2－4×3＝－3<0，故t 2－3t＋3>0恒成立，只要解不等式t 2－3t ＋3<1即可，即解不等式t 2－3t ＋2<0，解得1<t <2，故1<a x <2，取以a 为底的对数，根据对数函数性质得log a 2<x <0.正确选项为C.【提升训练】1．D 【解析】 M ∩N ＝N ⇔N ⊆M .当a ＝0时，N ＝∅，符合要求，当a ≠0时，只要a ＝1a，即a ＝±1即可．2．B 【解析】 当a >1时，函数f (x )＝log a x 在区间[a,2a ]上的最大值与最小值分别为log a 2a ＝log a 2＋1，log a a ＝1，它们的差为log a 2<1，即log 2a >1，故a >2；当0<a <1时，函数f (x )＝log a x 在区间[a,2a ]上的最大值与最小值分别为log a a ＝1，log a 2a ＝log a 2＋1，它们的差为－log a 2<1，即log a 2>－1，即log 2a <－1，即a <12.正确选项为B. 3．A 【解析】 设两直角边的长度分别是x ，y ，则0<x <1,0<y <1，随机事件“斜边的长小于34”满足x 2＋y 2<⎝ ⎛⎭⎪⎫342.把点(x ，y )看作平面上的点，则基本事件所在的区域的面积是1，随机事件所在的区域的面积是14π⎝ ⎛⎭⎪⎫342＝9π64. 4．D 【解析】 由sin x ＋cos x ＝13得1＋2sin x cos x ＝19，∴sin2x ＝－89<0，∴x ∈⎝ ⎛⎭⎪⎫π2，π， ∵(sin x －cos x )2＝1－sin2x ＝179且sin x >cos x ， ∴sin x －cos x ＝173.故选D. 5．1或－3 【解析】 当a >0时，函数y ＝a sin x ＋b 的最小值是－a ＋b ，最大值是a ＋b ，由－a ＋b ＝－1，a ＋b ＝3，解得a ＝2，b ＝1，此时a －b ＝1；a ＝0不符合要求；当a <0时，函数y ＝a sin x ＋b 的最小值是a ＋b ，最大值是－a ＋b ，由a ＋b ＝－1，－a ＋b ＝3，解得a ＝－2，b ＝1，此时a －b ＝－3.6．0 【解析】 结合图形可知，当A ，B ，M 均在圆上时，平行四边形OAMB 的对角线OM ＝2，此时四边形OAMB 为菱形，故问题等价于圆心到直线kx －y ＋1＝0的距离等于1.d ＝1k 2＋1＝1，解得k ＝0. 7．【解答】 ∵f (x )在区间(0，π)上是增函数，∴f ′(x )＝1－2m cos x ＋2⎝ ⎛⎭⎪⎫m －12cos2x ＝2[(2m －1)cos 2x －m cos x ＋1－m ]＝2(cos x －1)[(2m －1)cos x ＋(m －1)]>0在(0，π)上恒成立，令cos x ＝t ，则－1<t <1， 即不等式(t －1)[(2m －1)t ＋(m －1)]>0在(－1,1)上恒成立， ①若m >12，则t <1－m 2m －1在(－1,1)上恒成立，则只需1－m 2m －1≥1，即12<m ≤23； ②当m ＝12时，则0·t ＋12－1<0，在(－1,1)上显然成立； ③若m <12，则t >1－m 2m －1在(－1,1)上恒成立，则只需1－m 2m －1≤－1，即0≤m <12. 综上所述，所求实数m 的取值范围是⎣⎢⎡⎦⎥⎤0，23. 8．【解答】 (1)f ′(x )＝2x －2＋a x ＝2x 2－2x ＋a x，若函数f (x )是定义域上的单调函数，则只能f ′(x )≥0在(0，＋∞)上恒成立，即2x 2－2x ＋a ≥0在(0，＋∞)上恒成立，令g (x )＝2x 2－2x ＋a ，则函数g (x )图象的对称轴方程是x ＝12，故只要Δ＝4－8a ≤0恒成立，即只要a ≥12. (2)由(1)知当a ≥12时，f ′(x )＝0的点是导数不变号的点，故a ≥12时，函数无极值点； 当a <12时，f ′(x )＝0的根是x 1＝1－1－2a 2，x 2＝1＋1－2a 2， 若a ≤0，1－2a ≥1，此时x 1≤0，x 2>0，且在(0，x 2)上f ′(x )<0，在(x 2，＋∞)上f ′(x )>0，故函数f (x )有唯一的极小值点x 2＝1＋1－2a 2； 当0<a <12时，0<1－2a <1，此时x 1>0，x 2>0，f ′(x )在(0，x 1)，(x 2，＋∞)都大于0，f ′(x )在(x 1，x 2)上小于0，此时f (x )有一个极大值点x 1＝1－1－2a 2和一个极小值点x 2＝1＋1－2a 2. 综上可知，a ≤0时，f (x )在(0，＋∞)上有唯一的极小值点x 2＝1＋1－2a 2； 0<a <12时，f (x )有一个极大值点x 1＝1－1－2a 2和一个极小值点x 2＝1＋1－2a 2； a ≥12时，函数f (x )在(0，＋∞)上无极值点.。

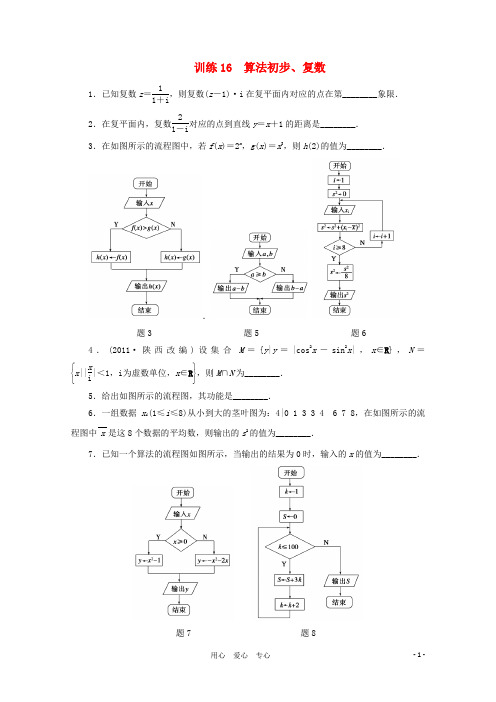
训练16 算法初步、复数1．已知复数z ＝11＋i ，则复数(z －1)·i 在复平面内对应的点在第________象限．2．在复平面内，复数21－i 对应的点到直线y ＝x ＋1的距离是________．3．在如图所示的流程图中，若f (x )＝2x，g (x )＝x 3，则h (2)的值为________．．题3 题5 题64．(2011·陕西改编)设集合M ＝{y |y ＝|cos 2x －sin 2x |，x ∈R }，N ＝⎩⎨⎧⎭⎬⎫x ||xi |＜1，i 为虚数单位，x ∈R ，则M ∩N 为________．5．给出如图所示的流程图，其功能是________．6．一组数据x i (1≤i ≤8)从小到大的茎叶图为：4|0 1 3 3 4 6 7 8，在如图所示的流程图中x 是这8个数据的平均数，则输出的s 2的值为________．7．已知一个算法的流程图如图所示，当输出的结果为0时，输入的x 的值为________．题7 题88．执行如图所示的流程图，则输出的S ＝________.9.若复数z 1＝4＋29i ，z 2＝6＋9i ，其中i 是虚数单位，则复数(z 1－z 2)i 的实部为________．10．已知集合A ＝⎩⎨⎧⎭⎬⎫12i，i 2，|5i 2|，＋2i，－i 22，则集合A ∩R ＋的子集个数为________．11．(2010·北京)在复平面内，复数2i1－i 对应的点的坐标为______．12．阅读如图所示的流程图，运行相应的程序，输出的结果是________．题12 题13 题1413．某地区为了解70岁～80岁的老人的日平均睡眠时间(单位：h)，随机选择了50位老人进行调查，下表是这50位老人睡眠时间的频率分布表：14．若如图所示的算法流程图中输出y 的值为0，则输入x 的值可能是________(写出所有可能的值)． 答案1．四 2.223．8 4.[)0，1 5．求|a－b|的值 6．7 7．－2或18．7 500 9．－20 10．8 11．(－1,1) 12．8 13．6.42 14．0，－3,1。

第7练 抓重点——函数性质与分段函数[题型分析·高考展望] 函数单调性、奇偶性、周期性是高考必考内容，以分段函数为载体是常考题型.主要以选择题或填空题的形式考查，难度为中档偏上.二轮复习中，应该重点训练函数性质的综合应用能力，收集函数应用的不同题型，分析比较异同点，排查与其他知识的交汇点，找到此类问题的解决策略，通过训练提高解题能力.常考题型精析题型一 函数单调性、奇偶性的应用1.常用结论：设x 1、x 2∈[a ，b ]，则(x 1－x 2) [f (x 1)－f (x 2)]>0⇔f (x 1)－f (x 2)x 1－x 2>0⇔f (x )在[a ，b ]上递增.(x 1－x 2)[f (x 1)－f (x 2)]<0⇔f (x 1)－f (x 2)x 1－x 2<0⇔f (x )在[a ，b ]上递减.2.若f (x )和g (x )都是增函数，则f (x )＋g (x )也是增函数，－f (x )是减函数，复合函数的单调性根据内函数和外函数同增异减的法则判断.3.定义域不关于原点对称的函数一定是非奇非偶函数.4.奇偶性相同的两函数的积为偶函数，奇偶性相反的两函数的积为奇函数.例1 (1)(2014·湖北)已知函数f (x )是定义在R 上的奇函数，当x ≥0时，f (x )＝12(|x －a 2|＋|x －2a 2|－3a 2).若∀x ∈R ，f (x －1)≤f (x )，则实数a 的取值范围为( ) A.[－16，16]B.[－66，66]C.[－13，13]D.[－33，33] (2)(2014·课标全国Ⅱ)已知偶函数f (x )在[0，＋∞)上单调递减，f (2)＝0.若f (x －1)>0，则x 的取值范围是________.点评 (1)奇偶性：具有奇偶性的函数在关于原点对称的区间上其图象、函数值、解析式和单调性联系密切，研究问题时可转化到只研究部分(一半)区间上，这是简化问题的一种途径.尤其注意偶函数f (x )的性质：f (|x |)＝f (x ).(2)单调性：可以比较大小，求函数最值，解不等式，证明方程根的唯一性.变式训练1 (1)(2015·天津)已知定义在R 上的函数f (x )＝2|x -m |－1(m 为实数)为偶函数，记a ＝f (log 0.53)，b ＝f (log 25)，c ＝f (2m )，则a ，b ，c 的大小关系为( ) A.a ＜b ＜c B.c ＜a ＜b C.a ＜c ＜bD.c ＜b ＜a(2)(2015·北京)下列函数中为偶函数的是( ) A.y ＝x 2sin x B.y ＝x 2cos x C.y ＝|ln x |D.y ＝2-x题型二 函数的周期性与对称性的应用重要结论：1.若对于定义域内的任意x ，都有f (a －x )＝f (a ＋x )，则f (x )关于x ＝a 对称. 2.若对于任意x 都有f (x ＋T )＝f (x )，则f (x )的周期为T .例2 (1)已知函数f (x )是(－∞，＋∞)上的奇函数，且f (x )的图象关于直线x ＝1对称，当x ∈[－1,0)时，f (x )＝－x ，则f (2 015)＋f (2 016)＝________.(2)定义在R 上的函数f (x )满足f (x ＋6)＝f (x ).当－3≤x <－1时，f (x )＝－(x ＋2)2；当－1≤x <3时，f (x )＝x ，则f (1)＋f (2)＋f (3)＋…＋f (2 016)＝________.点评 利用函数的周期性、对称性可以转化函数解析式、图象和性质，把不在已知区间上的问题，转化到已知区间上求解.变式训练2 已知定义在R 上的偶函数满足：f (x ＋4)＝f (x )＋f (2)，且当x ∈[0,2]时，y ＝f (x )单调递减，给出以下四个命题：①f (2)＝0；②x ＝－4为函数y ＝f (x )图象的一条对称轴；③函数y ＝f (x )在[8,10]上单调递增；④若方程f (x )＝m 在[－6，－2]上的两根为x 1，x 2，则x 1＋x 2＝－8. 则所有正确命题的序号为________. 题型三 分段函数例3 已知函数f (x )＝⎩⎨⎧－x 2＋2x ，x >0，0，x ＝0，x 2＋mx ，x <0是奇函数.(1)求实数m 的值；(2)若函数f (x )在区间[－1，a －2]上单调递增，求实数a 的取值范围.点评 (1)分段函数是一个函数在其定义域的不同子集上，因对应关系的不同而分别用几个不同的式子来表示的.分段函数的定义域等于各段函数的定义域的并集，其值域等于各段函数的值域的并集，分段函数虽由几个部分组成，但它表示的是一个函数.(2)在求分段函数f (x )解析式时，一定要首先判断x 属于定义域的哪个子集，然后再代入相应的关系式.变式训练3 (2014·浙江)设函数f (x )＝⎩⎨⎧x 2＋x ，x <0，－x 2，x ≥0. 若f (f (a ))≤2，则实数a 的取值范围是________.高考题型精练1.(2015·安徽)下列函数中，既是偶函数又存在零点的是( ) A.y ＝ln x B.y ＝x 2＋1 C.y ＝sin xD.y ＝cos x2.(2015·陕西)设f (x )＝⎩⎨⎧1－x ，x ≥0，2x，x ＜0，则f (f (－2))等于( )A.－1B.14 C.12D.323.(2014·山东)函数f (x )＝1(log 2x )2－1的定义域为( )A.⎝⎛⎭⎫0，12 B.(2，＋∞)C.⎝⎛⎭⎫0，12∪(2，＋∞) D.⎝⎛⎦⎤0，12∪[2，＋∞) 4.(2014·江西)已知函数f (x )＝⎩⎪⎨⎪⎧a ·2x ，x ≥0，2-x ，x <0(a ∈R )，若f [f (－1)]＝1，则a 等于( ) A.14 B.12 C.1D.25.下列函数f (x )中，满足“∀x 1，x 2∈(0，＋∞)，且x 1≠x 2，(x 1－x 2)[f (x 1)－f (x 2)]<0”的是( ) A.f (x )＝1x －xB.f (x )＝x 3C.f (x )＝ln xD.f (x )＝2x6.函数y ＝f (x －1)的图象关于直线x ＝1对称，当x ∈(－∞，0)时，f (x )＋xf ′(x )<0成立，若a ＝20.2·f (20.2)，b ＝ln 2·f (ln 2)，c ＝(log 1214)·f (log 1214)，则a ，b ，c 的大小关系是( )A.a >b >cB.b >a >cC.c >a >bD.a >c >b7.设函数g (x )＝x 2－2(x ∈R )，f (x )＝⎩⎨⎧g (x )＋x ＋4，x <g (x )，g (x )－x ，x ≥g (x )， 则f (x )的值域是( )A.[－94，0]∪(1，＋∞)B.[0，＋∞)C.[－94，＋∞)D.[－94，0]∪(2，＋∞)8.(2015·青岛模拟)对实数a 和b ，定义运算“⊗”：a ⊗b ＝⎩⎪⎨⎪⎧a ，a －b ≤1，b ，a －b >1.设函数f (x )＝(x 2－2)⊗(x－x 2)，x ∈R .若函数y ＝f (x )－c 的图象与x 轴恰有两个公共点，则实数c 的取值范围是( ) A.(－∞，－2]∪(－1，32)B.(－∞，－2]∪(－1，－34)C.(－1，14)∪(14，＋∞)D.(－1，－34)∪[14，＋∞)9.(2014·安徽)若函数f (x )(x ∈R )是周期为4的奇函数，且在[0,2]上的解析式为f (x )＝⎩⎨⎧x (1－x )，0≤x ≤1，sin πx ，1<x ≤2，则f ⎝⎛⎭⎫294＋f ⎝⎛⎭⎫416＝________. 10.对于任意实数a ，b ，定义min{a ，b }＝⎩⎪⎨⎪⎧a ，a ≤b ，b ，a >b .设函数f (x )＝－x ＋3，g (x )＝log 2x ，则函数h (x )＝min{f (x )，g (x )}的最大值是________.11.已知函数f (x )＝⎩⎨⎧x －[x ]，x ≥0，f (x ＋1)，x <0其中[x ]表示不超过x 的最大整数.若直线y ＝k (x ＋1)(k >0)与函数y ＝f (x )的图象恰有三个不同的交点，则实数k 的取值范围是____________. 12.已知函数y ＝f (x )，x ∈R ，有下列4个命题：①若f (1＋2x )＝f (1－2x )，则f (x )的图象关于直线x ＝1对称； ②y ＝f (x －2)与y ＝f (2－x )的图象关于直线x ＝2对称；③若f (x )为偶函数，且f (2＋x )＝－f (x )，则f (x )的图象关于直线x ＝2对称； ④若f (x )为奇函数，且f (x )＝f (－x －2)，则f (x )的图象关于直线x ＝1对称. 其中正确命题的序号为________.答案精析第7练 抓重点——函数性质与分段函数常考题型精析 例1 (1)B (2)(－1,3)解析 (1)因为当x ≥0时，f (x )＝12(|x －a 2|＋|x －2a 2|－3a 2)，所以当0≤x ≤a 2时，f (x )＝12(a 2－x ＋2a 2－x －3a 2)＝－x ；当a 2<x <2a 2时，f (x )＝12(x －a 2＋2a 2－x －3a 2)＝－a 2；当x ≥2a 2时，f (x )＝12(x －a 2＋x －2a 2－3a 2)＝x －3a 2.综上，函数f (x )＝12(|x －a 2|＋|x －2a 2|－3a 2)在x ≥0时的解析式等价于f (x )＝⎩⎪⎨⎪⎧－x ，0≤x ≤a 2，－a 2，a 2<x <2a 2，x －3a 2，x ≥2a 2.因此，根据奇函数的图象关于原点对称作出函数f (x )在R 上的大致图象如下，观察图象可知，要使∀x ∈R ，f (x －1)≤f (x )，则需满足2a 2－(－4a 2)≤1，解得－66≤a ≤66. (2)∵f (x )是偶函数， ∴图象关于y 轴对称.又f (2)＝0，且f (x )在[0，＋∞)单调递减，则f (x )的大致图象如图所示，由f (x －1)>0，得－2<x －1<2，即－1<x <3. 变式训练1 (1)B (2)B解析 (1)由函数f (x )＝2|x －m |－1为偶函数，得m ＝0，∴f (x )＝2|x |－1，当x ＞0时，f (x )为增函数，log 0.53＝－log 23，∴log 25＞|－log 23|＞0，∴b ＝f (log 25)＞a ＝f (log 0.53)＞c ＝f (2m )＝f (0)， 故选B.(2)由f (－x )＝f (x )，且定义域关于原点对称，可知A 为奇函数，B 为偶函数，C 定义域不关于原点对称，D 为非奇非偶函数. 例2 (1)1 (2)336解析 (1)由f (x )是(－∞，＋∞)上的奇函数且f (x )的图象关于直线x ＝1对称，知f (x )的周期为4， f (2 015)＝f (3)＝f (－1)＝1， f (2 016)＝f (4)＝f (0)＝0. ∴f (2 015)＋f (2 016)＝1＋0＝1.(2)由f (x ＋6)＝f (x )可知，函数f (x )的一个周期为6，所以f (－3)＝f (3)＝－1，f (－2)＝f (4)＝0，f (－1)＝f (5)＝－1，f (0)＝f (6)＝0，f (1)＝1，f (2)＝2，所以在一个周期内有f (1)＋f (2)＋…＋f (6)＝1＋2－1＋0－1＋0＝1，所以f (1)＋f (2)＋…＋f (2 016)＝[f (1)＋f (2)＋…＋f (6)]×336＝336. 变式训练2 ①②④解析 令x ＝－2，得f (2)＝f (－2)＋f (2)，f (－2)＝0，又函数f (x )是偶函数，故f (2)＝0，①正确； 根据①可得f (x ＋4)＝f (x )，可得函数f (x )的周期是4，由于偶函数的图象关于y 轴对称，故x ＝－4也是函数y ＝f (x )图象的一条对称轴，②正确； 根据函数的周期性可知，函数f (x )在[8,10]上单调递减，③不正确； 由于函数f (x )的图象关于直线x ＝－4对称，故如果方程f (x )＝m 在区间[－6，－2]上的两根为x 1，x 2，则x 1＋x 22＝－4，即x 1＋x 2＝－8，④正确.故正确命题的序号为①②④.例3 解 (1)∵函数f (x )是奇函数，∴f (－x )＝－f (x ). 当x >0时，－x <0，有(－x )2－mx ＝－(－x 2＋2x )， 即x 2－mx ＝x 2－2x . ∴m ＝2.(2)由(1)知f (x )＝⎩⎪⎨⎪⎧－x 2＋2x ，x >0，0，x ＝0，x 2＋2x ，x <0，如图.当x >0时，f (x )＝－x 2＋2x ＝－(x －1)2＋1， ∴当x ∈[1，＋∞)时，f (x )单调递减； 当x ∈(0,1]时，f (x )单调递增.当x <0时，f (x )＝x 2＋2x ＝(x ＋1)2－1， ∴当x ∈(－∞，－1]时，f (x )单调递减； 当x ∈[－1,0)时，f (x )单调递增. 综上知：函数f (x )在[－1,1]上单调递增. 又函数f (x )在区间[－1，a －2]上单调递增.∴⎩⎪⎨⎪⎧a －2>－1，a －2≤1，解得1<a ≤3. 故实数a 的取值范围是(1,3]. 变式训练3 a ≤ 2解析 f (x )的图象如图，由图象知，满足f (f (a ))≤2时，得f (a )≥－2，而满足f (a )≥－2时，得a ≤2.高考题型精练1.D [对数函数y ＝ln x 是非奇非偶函数；y ＝x 2＋1为偶函数但没有零点；y ＝sin x 是奇函数；y ＝cos x 是偶函数且有零点，故选D.]2.C [∵f (－2)＝2－2＝14＞0，则f (f (－2))＝f ⎝⎛⎭⎫14＝1－14＝1－12＝12，故选C.] 3.C [由题意知⎩⎪⎨⎪⎧x >0，(log 2x )2>1，解得x >2或0<x <12.故选C.]4.A [由题意得f (－1)＝2－(－1)＝2，f [f (－1)]＝f (2)＝a ·22＝4a ＝1，∴a ＝14.]5.A [“∀x 1，x 2∈(0，＋∞)，且x 1≠x 2，(x 1－x 2)·[f (x 1)－f (x 2)]<0”等价于在(0，＋∞)上f (x )为减函数，易判断f (x )＝1x－x 符合.]6.B [因为函数y ＝f (x －1)的图象关于直线x ＝1对称，所以y ＝f (x )关于y 轴对称. 所以函数y ＝xf (x )为奇函数. 因为[x f (x )]′＝f (x )＋xf ′(x )，所以当x ∈(－∞，0)时，[x f (x )]′＝f (x )＋xf ′(x )<0， 函数y ＝xf (x )单调递减，从而当x ∈(0，＋∞)时，函数y ＝xf (x )单调递减. 因为1<20.2<2,0<ln 2<1，log 1214＝2， 从而0<ln 2<20.2<log 1214，所以b >a >c .]7.D [由x <g (x )得x <x 2－2， ∴x <－1或x >2；由x ≥g (x )得x ≥x 2－2，∴－1≤x ≤2.∴f (x )＝⎩⎪⎨⎪⎧x 2＋x ＋2，x <－1或x >2，x 2－x －2，－1≤x ≤2.即f (x )＝⎩⎨⎧(x ＋12)2＋74，x <－1或x >2，(x －12)2－94，－1≤x ≤2.当x <－1时，f (x )>2；当x >2时，f (x )>8.∴当x ∈(－∞，－1)∪(2，＋∞)时，函数的值域为(2，＋∞). 当－1≤x ≤2时，－94≤f (x )≤0.∴当x ∈[－1,2]时，函数的值域为[－94，0].综上可知，f (x )的值域为[－94，0]∪(2，＋∞).]8.B [f (x )＝⎩⎪⎨⎪⎧x 2－2，x 2－2－(x －x 2)≤1，x －x 2，x 2－2－(x －x 2)>1，即f (x )＝⎩⎨⎧x 2－2，－1≤x ≤32，x －x 2，x <－1或x >32，f (x )的图象如图所示，由图象可知B 正确.]9.516解析 ∵f (x )是以4为周期的奇函数， ∴f ⎝⎛⎭⎫294＝f ⎝⎛⎭⎫8－34＝f ⎝⎛⎭⎫－34， f ⎝⎛⎭⎫416＝f ⎝⎛⎭⎫8－76＝f ⎝⎛⎭⎫－76.∵当0≤x ≤1时，f (x )＝x (1－x )， ∴f ⎝⎛⎭⎫34＝34×⎝⎛⎭⎫1－34＝316. ∵当1<x ≤2时，f (x )＝sin πx ， ∴f ⎝⎛⎭⎫76＝sin 7π6＝－12. 又∵f (x )是奇函数，∴f ⎝⎛⎭⎫－34＝－f ⎝⎛⎭⎫34＝－316， f ⎝⎛⎭⎫－76＝－f ⎝⎛⎭⎫76＝12.11 ∴f ⎝⎛⎭⎫294＋f ⎝⎛⎭⎫416＝－316＋12＝516. 10.1解析 依题意，得h (x )＝⎩⎪⎨⎪⎧log 2x ，0<x ≤2，－x ＋3，x >2.当0<x ≤2时，h (x )＝log 2x 是增函数；当x >2时，h (x )＝3－x 是减函数，∴h (x )在x ＝2时取得最大值h (2)＝1.11.⎣⎡⎭⎫14，13解析 根据[x ]表示的意义可知，当0≤x <1时，f (x )＝x ，当1≤x <2时，f (x )＝x －1，当2≤x <3时，f (x )＝x －2，以此类推，当k ≤x <k ＋1时，f (x )＝x －k ，k ∈Z ，当－1≤x <0时，f (x )＝x ＋1，作出函数f (x )的图象如图，直线y ＝k (x ＋1)过点(－1,0)，当直线经过点(3,1)时恰有三个交点，当直线经过点(2,1)时恰好有两个交点，在这两条直线之间时有三个交点，故k ∈⎣⎡⎭⎫14，13.12.①②④解析 1＋2x ＋1－2x 2＝1，故函数y ＝f (x )的图象关于直线x ＝1对称，故①正确；对于②，令t ＝x －2，则问题等价于y ＝f (t )与y ＝f (－t )图象的对称问题，显然这两个函数的图象关于直线t ＝0对称，即函数y ＝f (x －2)与y ＝f (2－x )的图象关于直线x －2＝0即x ＝2对称，故②正确；由f (x ＋2)＝－f (x )，可得f (x ＋4)＝－f (x ＋2)＝f (x )，我们只能得到函数的周期为4，即只能推得函数y ＝f (x )的图象关于直线x ＝4k (k ∈Z )对称，不能推得函数y ＝f (x )的图象关于直线x ＝2对称，故③错误；由于函数f (x )为奇函数，由f (x )＝f (－x －2)，可得f (－x )＝f (x ＋2)，由于－x ＋x ＋22＝1，可得函数y ＝f (x )的图象关于直线x ＝1对称，故④正确.。

训练15 概率与统计1．一个篮球运动员投篮一次得3分的概率为a ，得2分的概率为b ，不得分的概率为c (a 、b 、c ∈(0,1))，已知他投篮一次得分的数学期望为1(不计其他得分的情况)，则ab 的最大值为________．2．已知某一随机变量X 的概率分布表如下，且E (X )＝6.3，则a 的值为________.3.1、2、3、4、5、6)，骰子朝上的面的点数分别为x 、y ，则log 2x y ＝1的概率为________．4．已知函数f (x )＝x 2＋bx ＋c ，其中0≤b ≤4,0≤c ≤4，记函数f (x )满足条件⎩⎪⎨⎪⎧f (2)≤12f (－2)≤4为事件A ，则事件A 发生的概率为________．5．甲、乙两人进行围棋比赛，比赛采取五局三胜制，无论哪一方先胜三局则比赛结束，假定甲每局比赛获胜的概率均为23，则甲以3∶1的比分获胜的概率为________． 6．如果ξ～B ⎝⎛⎭⎫15，14，则使P (ξ＝k )取最大值的k 值为________． 7．(2011·锦州模拟)甲射击命中目标的概率是12，乙命中目标的概率是13，丙命中目标的概率是14.现在三人同时射击目标，则目标被击中的概率为________． 8．(2011·辽宁)从1,2,3,4,5中任取2个不同的数，事件A ＝“取到的2个数之和为偶数”，事件B ＝“取到的2个数均为偶数”，则P (B |A )＝________.9.甲、乙两人进行5场比赛，每场甲获胜的概率为23，乙获胜的概率为13，如果有一人胜了三场，比赛即告结束，那么比赛以乙获胜3场负2场而结束的概率是________．10．(2010·福建)某次知识竞赛规则如下：在主办方预设的5个问题中，选手若能连续正确回答出两个问题，即停止答题，晋级下一轮．假设某选手正确回答每个问题的概率都是0.8，且每个问题的回答结果相互独立，则该选手恰好回答了4个问题就晋级下一轮的概率为________．11．已知样本容量为30，在样本频率分布直方图中，各小长方形的高的比从左到右依次为2∶4∶3∶1，则第2组的频率和频数分别是________．12．学校为了调查学生在课外读物方面的支出情况 ，抽取了一个容量为n 的样本，其频率分布直方图如图所示，其中支出在[50,60)的同学有30人，若想在这n 个人中抽取50个人，则在[50,60)之间应抽取的人数为________．13．在如图所示的“茎叶图”表示的数据中，众数和中位数分别为________________.14.(2010·福建)将容量为n的样本中的数据分成6组，绘制频率分布直方图，若第一组至第六组数据的频率之比为2∶3∶4∶6∶4∶1，且前三组数据的频数之和等于27，则n＝________.答案1.1242．7 3.112 4.12 5.8276．3或4 7.348.149.88110．0.12811．0.4,12 12．15 13．31,26 14．60。

第 7 练抓要点——函数性质与分段函数[ 题型剖析·高考展望 ]函数单一性、奇偶性、周期性是高考必考内容，以分段函数为载体是常考题型．主要以填空题的形式考察，难度为中档偏上．二轮复习中，应当要点训练函数性质的综合应用能力，采集函数应用的不一样题型，剖析比较异同点，排查与其余知识的交汇点，找到此类问题的解决议略，经过训练提升解题能力．体验高考1 ． (2015 山·东改编 )设函数f(x)＝3x－ 1， x＜ 1，f(f(a)) ＝ 2f(a)的 a 的取值范围是则知足2x， x≥1，________ ．答案2，＋∞3分析由 f(f( a)) ＝ 2f(a)得， f(a) ≥1.2 2 当 a<1 时，有 3a－1≥1，∴ a≥，∴≤a<1.3 3 当 a≥1时，有 2a≥1，∴ a≥0，∴ a≥ 1.2综上， a≥ .32． (2015 山·东改编 )设函数 f(x)＝3x－b， x＜ 1，5＝ 4，则 b 等于 ________．x若 f f2 ， x≥1.6答案1 2分析由题意，得 f 555－ b. 6＝ 3× － b＝62535b1.当－ b≥1，即 b≤时，22＝ 4，解得 b＝222当52－ b＜ 1，即 b＞32时， 3×52－ b － b＝4，7解得 b＝8( 舍去 )．1因此 b＝ .23x －3x， x≤a，3． (2016 ·京北 )设函数 f(x)＝－2x，x＞a.(1)若 a＝ 0，则 f(x)的最大值为 ________；(2)若 f(x)无最大值，则实数 a 的取值范围是 ________．答案 (1)2 (2)(－∞，－ 1)3x － 3x， x≤0，分析(1)当 a＝0 时， f(x)＝－2x，x＞ 0.若 x≤0， f′(x)＝ 3x2－3＝ 3(x2－ 1)．由 f′(x)＞ 0 得 x＜－ 1，由 f′(x)＜0 得－ 1＜x≤0.因此 f( x)在 (－∞，－ 1)上单一递加；在 (－ 1,0] 上单一递减，因此 f( x)的最大值为 f(－ 1)＝ 2.若 x＞ 0， f(x)＝－ 2x 单一递减，因此f(x)＜ f(0)＝ 0.因此 f( x)的最大值为 2.(2)f(x)的两个函数在无穷制条件时的图象如图．由 (1) 知，当 a≥－ 1 时， f(x)获得最大值2.当 a＜－ 1 时， y＝－ 2x 在 x＞ a 时无最大值，且－ 2a＞ 2.因此 a＜－ 1.1－ x， x≥0，则 f(f(－ 2))等于 ________．4． (2015 陕·西改编 )设 f(x)＝x2 ， x＜ 0，答案1 2分析∵ f(－ 2)＝ 2－2＝1＞ 0，则 f(f(－ 2))＝ f1＝1－1＝ 1－1＝1.444225． (2016 四·川 )已知函数 f(x)是定义在 R 上的周期为 2 的奇函数，当0<x<1 时， f(x)＝ 4x，则f－5＋ f(1) ＝________.2答案－ 2分析因为 f(x)是周期为 2 的函数，因此 f( x)＝ f(x＋ 2)．而 f(x)是奇函数，因此 f( x)＝－ f(－ x)．因此 f(1) ＝ f(－ 1)， f(1)＝－ f(－ 1)，即 f(1) ＝0，又 f －5＝ f －1＝－ f1， f11＝42＝ 2，222255故 f －2＝－ 2，进而 f －2＋ f(1) ＝－ 2.高考必会题型题型一函数单一性、奇偶性的应用1．常用结论：设x1、 x2∈ [a， b]，则(x1－ x2) [f(x1)－ f(x2)]>0 ?f(x1)－ f(x2)>0 ? f(x)在[ a， b] 上x1－ x2单一递加． (x1－x2)[f( x1)－ f(x2)]<0 ?f(x1 )－ f(x2)<0? f(x)在 [a， b]上单一递减．x1－ x22．若 f(x)和 g(x)都是增函数，则 f(x)＋ g(x)也是增函数，－ f(x)是减函数，复合函数的单一性依据内函数和外函数同增异减的法例判断．3．定义域不对于原点对称的函数必定是非奇非偶函数．4．奇偶性同样的两函数的积为偶函数，奇偶性相反的两函数的积为奇函数．例 1 (1) 假如函数f(x)＝ ax2＋ 2x－3 在区间 (－∞， 4)上是单一递加的，则实数 a 的取值范围是 ________．(2 － a) x＋1， x＜ 1，(2) 已知 f(x)＝知足对随意 x1≠x2，都有f(x1)－f( x2)＞ 0 建立，那么 a 的取a x， x≥1x1－ x2值范围是 ________．答案(1)[－1， 0] (2)[3， 2) 42分析(1)当 a＝0 时， f(x)＝2x－ 3，在定义域 R 上是单一递加的，故在(－∞，4)上单一递加；当 a≠0时，二次函数f( x)的对称轴为x＝－1a.因为 f( x)在 (－∞，4) 上单一递加，因此 a＜ 0，且－1a≥4，解得－14≤a＜0.综合上述得，－14≤a≤0. (2)由已知条件得 f(x)为增函数，2－ a＞0，∴a＞ 1，(2 －a) ×1＋ 1≤a，解得3≤a＜ 2，∴ a 的取值范围是 [3， 2)．22评论(1) 奇偶性：拥有奇偶性的函数在对于原点对称的区间上其图象、函数值、分析式和单一性联系亲密，研究问题时可转变到只研究部分( 一半 )区间上，这是简化问题的一种途径．特别注意偶函数f(x)的性质： f(|x|)＝ f(x)．(2)单一性：能够比较大小，求函数最值，解不等式，证明方程根的独一性．变式训练1若 f(x)＝－ x2＋ 2ax 与g( x)＝a在区间[1,2] 上都是减函数，则 a 的取值范围是x＋1________ ．答案(0,1]分析由 f(x)＝－ x2＋ 2ax 在 [1,2] 上是减函数可得[1,2] ? [a，＋∞)，∴ a≤ 1.∵y＝1在 ( －1，＋∞)上为减函数，x＋ 1a∴由 g(x)＝在[1,2]上是减函数可得a＞0，故 0＜ a≤1.题型二函数的周期性与对称性的应用重要结论： 1.若对于定义域内的随意x，都有 f(a－ x)＝ f(a＋ x)，则函数＝ a 对称．2．若对于随意x，都有 f(x＋ T)＝ f(x)，则 f(x)为周期函数，且它的周期为例 2 (1) 已知函数f(x)是 (－∞，＋∞)上的奇函数，且 f(x)的图象对于直线f(x)的图象对于直线xT.x＝ 1 对称，当 x∈ [ －1,0)时， f(x)＝－ x，则 f(2015) ＋ f(2016) ＝ ________.(2) 定义在 R 上的函数 f(x)知足 f(x＋ 6)＝ f( x)．当－ 3≤x＜－ 1 时， f(x)＝－ (x＋ 2)2；当－ 1≤x＜3时， f(x)＝ x，则 f(1) ＋ f(2)＋ f(3) ＋＋ f(2016) ＝ ________.答案 (1)1 (2)336分析(1)由 f(x)是( －∞，＋∞)上的奇函数且f(x) 的图象对于直线x＝ 1 对称，知 f(x)的周期为4，∴f(2015) ＝f(3) ＝ f(－ 1)＝ 1，f(2016) ＝ f(4)＝ f(0) ＝ 0.∴f(2015) ＋f(2016) ＝1＋ 0＝ 1.(2) 由 f(x＋ 6)＝ f(x)可知，函数 f(x)的一个周期为 6，因此 f(－ 3)＝ f(3) ＝－ 1， f(－ 2)＝ f(4) ＝ 0，f(－1)＝ f(5)＝－ 1，f(0) ＝ f(6)＝ 0，f(1) ＝ 1，f(2)＝ 2，因此在一个周期内有 f(1) ＋f(2) ＋＋f(6)＝1＋ 2－ 1＋ 0－ 1＋0＝ 1，因此 f(1) ＋ f(2)＋＋ f(2016) ＝ [f(1) ＋f(2)＋＋f(6)] ×336＝ 336.评论利用函数的周期性、对称性能够转变函数分析式、图象和性质，把不在已知区间上的问题，转变到已知区间上求解．变式训练2已知函数y＝ f(x)是定义在R 上的奇函数，? x∈ R，f(x－ 1)＝ f(x＋ 1)建立，当f(x2)－ f(x1)x∈ (0,1)且 x1≠x2时，有＜0，给出以下命题：①f(1)＝ 0；②f(x)在 [ － 2,2] 上有 5 个零点；③点 (2014,0) 是函数 y＝ f(x)图象的一个对称中心；④直线 x＝2014 是函数 y＝ f(x)图象的一条对称轴．则正确命题的序号是________．答案①②③分析在 f(x－ 1)＝ f(x＋ 1)中令x＝ 0，得f(－1)＝ f(1)，又f(－ 1)＝－ f(1)，∴ 2f(1)＝ 0，∴ f(1)＝ 0，故①正确；由 f(x － 1)＝ f(x ＋ 1)，得 f(x)＝ f( x ＋2) ，∴ f(x)是周期为 2 的周期函数，∴ f(2)＝ f(0)＝ 0，又当 x ∈ (0,1)且 x 1≠x 2 时，有 f(x 2)－f(x 1)＜0，x 2－x 1 ∴函数在区间 (0,1)上单一递减，可作函数的简图如图．由图知②③也正确，④不正确．因此正确命题的序号为①②③ .题型三 分段函数例 3(1)(2016 ·江苏 )设 f(x)是定义在R 上且周期为 2 的函数，在区间[ － 1,1)上， f( x)＝x ＋ a ，－ 1≤x ＜ 0，592此中 a ∈ R.若 f－ 2 ＝ f 2 ，则 f(5a)的值是 ________．5－ x ， 0≤x ＜ 1，(2)(2016 青·岛模拟 )对实数 a 和 b ，定义运算 “?”： a?b ＝a ， a －b ≤1，设函数 f(x)＝ (x 2－ 2)?b ， a －b ＞ 1.( x －x 2)， x ∈ R.若函数 y ＝ f(x)－ c 的图象与 x 轴恰有两个公共点，则实数 c 的取值范围是________ ．答案(1)－2(2)( － ∞，－ 2]∪ (－ 1，－ 3)54分析(1)由已知 f －5＝ f － 5＋ 2 ＝ f －12 2 21＝－ ＋ a ，f 9＝ f 9－4 ＝ f 1 ＝ 2－1＝1222 5 210.又∵ f －52 ＝f 92 ，则－ 12＋ a ＝ 101， a ＝ 35，3 2 ∴ f(5a)＝ f(3)＝ f(3 －4)＝ f(－ 1)＝－ 1＋ ＝－ .55x 2－ 2， x 2－ 2－ (x －x 2)≤1，(2) f(x)＝x － x 2， x 2－ 2－ (x － x 2)＞ 1，23x － 2，－ 1≤x ≤ ，2即 f(x)＝x － x 2， x ＜－ 1或 x ＞32.3f(x)的图象如下图，由图象可知c 的范围是 (－ ∞，－ 2]∪ (－ 1，－ 4)．评论(1) 分段函数是一个函数在其定义域的不一样子集上，因对应关系的不一样而分别用几个不一样的式子来表示的． 分段函数的定义域等于各段函数的定义域的并集， 其值域等于各段函数的值域的并集，分段函数虽由几个部分构成，但它表示的是一个函数．(2) 在求分段函数 f(x)的分析式时，必定要第一判断 x 属于定义域的哪个子集，而后再代入相应的关系式．变式训练 3 已知函数 f(x)＝x 2＋ 1， x ≥0，则知足不等式 f(1 －x 2)＞f(2x)的 x 的取值范围是1， x ＜0，________ ． 答案(－ 1， 2－ 1)2分析x ＋ 1， x ≥0，画出 f(x)＝的图象如图．1， x ＜ 0由图象可知，若f(1－ x 2)＞ f(2x)，1－ x 2＞ 0， 则1－ x 2＞ 2x ，－ 1＜ x ＜ 1，即－ 1－ 2＜ x ＜－ 1＋ 2，得 x ∈ (－ 1， 2－ 1)．高考题型精练1．设函数 f(x)为偶函数，对于随意的 x ＞0，都有 f(2＋ x)＝－ 2f(2－ x)，已知 f( － 1)＝ 4，那么f(－ 3)等于 ______．答案－ 8分析∵ f(x)为偶函数，∴f(1)＝ f(－ 1)＝ 4， f(－ 3)＝ f(3) ，当x＝ 1 时， f(2＋ 1)＝－ 2·f(2 － 1) ，∴f(3)＝－ 2×4＝－ 8，∴f(－ 3)＝－ 8.2．已知函数 f( x)为 R 上的减函数，则知足 f 1＜ f(1)的实数 x 的取值范围是 ________．x答案(－ 1,0)∪(0,1)分析由 f(x)为 R 上的减函数且 f 1，＜f(1)x1得x＞ 1，即 |x|＜ 1，x≠0，x≠ 0.∴－ 1＜ x＜0 或 0＜ x＜ 1.3．设函数 f(x)＝－ x2＋4x， x≤4，若函数 y＝ f(x)在区间 (a，a＋ 1)上单一递加，则实数 a 的log 2x， x＞4，取值范围是 ________．答案(－∞，1]∪[4，＋∞)分析如图，－ x2＋ 4x， x≤4，y＝f(x)在区间 (a， a＋ 1)上单一递加，则 a 画出 f( x)＝的图象，若使函数log 2x，x＞ 4＋ 1≤2或 a≥4，解得实数 a 的取值范围是 (－∞， 1]∪ [4，＋∞)．4． (2015 课·标全国Ⅱ改编 )设函数 f(x)＝ ln(1 ＋ |x|)－12，则使得 f(x) ＞f(2x－ 1)建立的 x 的1＋ x 取值范围是 ________．答案1，131分析由 f(x)＝ ln(1 ＋ |x|)－1＋x2，知 f(x) 为 R 上的偶函数，于是 f(x)＞ f(2x－ 1)即为 f(|x|)＞ f(|2x － 1|)．当 x＞ 0 时， f(x)＝ ln(1＋ x)－12，f′(x)＝ 1 ＋2x 22＞0，因此f(x)在[0，＋∞)上是增函1＋ x1＋ x(1＋ x )数，则由f(|x|)＞ f(|2x－ 1|)得 |x|＞ |2x－ 1|，平方得3x2－ 4x＋ 1＜ 0，解得1＜ x＜ 1. 35．已知函数f(x)是定义在R 上的奇函数，当数 a 的取值范围是________．答案(－ 2,1)x≥0时， f(x)＝ x2＋ 2x，若f(2－ a2)＞ f(a)，则实分析∵ f(x)是奇函数，∴当 x＜0 时， f(x) ＝－ x2＋ 2x.作出函数 f(x)的大概图象如图中实线所示，联合图象可知 f(x)是 R 上的增函数，由 f(2－ a2)＞ f( a) ，得 2－ a2＞ a，解得－ 2＜a＜ 1.6．函数 y＝ f(x－ 1)的图象对于直线 x＝ 1 对称，当x∈ (－∞， 0)时， f(x)＋ xf′(x)<0 建立，若 a＝ 20.2·f(20.2)， b＝ ln2 f(ln2)·，c (log11) f (log11) ，则a，b，c的大小关系是________．2424答案b>a>c分析因为函数 y＝ f(x－ 1)的图象对于直线x＝ 1 对称，因此 y＝ f( x)对于 y 轴对称．因此函数 y＝ xf(x)为奇函数．因为当 x∈ (－∞，0) 时， [xf(x)] ＝′f(x)＋ xf′(x)<0 ，因此函数y＝ xf(x)在 (－∞， 0)上单一递减，进而当 x∈ (0，＋∞)时，函数y＝xf(x)单一递减．因为 1<2 0.2<2,0<ln2<1 ，log11＝2，24进而 0<ln2<2 0.2< log211 ，4因此 b>a>c.7．(2016 四·川改编 )某企业为激励创新，计划逐年加大研发资本投入．若该企业2015 年整年投入研发资本 130 万元．在此基础上，每年投入的研发资本比上一年增加12%，则该企业全年投入的研发资本开始超出200 万元的年份是 ________．( 参照数据： lg1.12＝ 0.05， lg1.3＝ 0.11， lg2 ＝ 0.30)答案2019分析设第 x 年的研发资本为 200 万元，则由题意可得 130×(1＋ 12%)x＝ 200，∴ 1.12x＝20，∴ x＝ log1.1220＝ log 1.1220－ log 1.1213 1313＝l g20 － lg13lg1.12 lg1.12＝(lg2 ＋lg10) － (lg1.3 ＋ lg10)lg1.120.3＋ 1－ 0.11－ 1≈＝3.8.0.05即 3 年后不到 200 万元，第 4 年超出 200 万元，即 2019 年超出 200 万元．8．已知函数 f( x)在实数集 R 上拥有以下性质：①直线 x ＝1 是函数 f(x)的一条对称轴；② f(x ＋ 2)＝－ f(x)；③当 1≤x 1＜x 2≤3时， (f( x 2)－ f(x 1 )) (x ·2－ x 1)＜ 0，则 f(2015) ， f(2016) ， f(2017) 从大到小的次序为____________________ ．答案 f(2017) ＞ f(2016) ＞ f(2015)分析由 f(x ＋ 2)＝－ f(x)，得 f(x ＋ 4)＝ f(x)，因此函数 f( x)的周期是 4.因此 f(2015) ＝ f(3) ， f(2016) ＝ f(0)， f(2017) ＝ f(1) ，又直线 x ＝1 是函数 f(x)的一条对称轴，因此 f(2016) ＝ f(0) ＝ f(2)．由当 1≤x 1＜x 2≤3时， (f( x 2)－ f(x 1 )) (x ·2－ x 1)＜ 0，可知当 1≤x 1＜ x 2≤3时，函数单一递减，因此 f(1) ＞ f(2)＞ f(3) ，故 f(2017) ＞ f(2016) ＞ f(2015) ．9．已知函数 f(x)＝ x － [ x] ， x ≥0，此中 [x]表示不超出 x 的最大整数． 若直线 y ＝ k(x ＋ 1)(k>0)f(x ＋ 1)， x<0 的图象与函数 y ＝ f(x)的图象恰有三个不一样的交点，则实数 k 的取值范围是 ____________ ．答案1，14 3分析 依据 [x]表示的意义可知，当 0≤x<1 时， f(x)＝ x ，当 1≤x<2 时， f(x) ＝x － 1，当 2≤x<3时， f(x)＝ x － 2，以此类推，当 k ≤x<k ＋ 1 时， f(x) ＝x － k ， k ∈ Z 且 k ＞0.当－ 1≤x<0 时， f(x) ＝ x ＋ 1，作出函数 f( x)的图象如图．直线 y ＝ k(x ＋ 1)过点 (－ 1,0)，当直线经过点 (3,1)时恰有三个交点，当直线经过点(2,1) 时恰巧有两个交点，在这两条直线之间时有三个交点，故1 1 k ∈ 4， 3 .10．已知函数y ＝ f(x)， x ∈ R ，有以下 4 个命题：①若f(1＋ 2x)＝ f(1 －2x)，则f(x)的图象对于直线x ＝ 1 对称；② y ＝ f( x －2)与y ＝ f(2－ x)的图象对于直线x ＝2 对称；③若f( x)为偶函数，且f(2＋x)＝－ f(x)，则f(x)的图象对于直线x ＝2 对称；④若 f( x)为奇函数，且f(x)＝ f(－ x－ 2)，则 f(x)的图象对于直线x＝ 1 对称．此中正确命题的序号为________．答案①②④分析1＋2x＋1－2x＝ 1，故函数 y＝ f(x)的图象对于直线 x＝1对称，故①正确；对于②，令2t ＝ x－2，则问题等价于y＝f(t)与 y＝ f( －t)图象的对称问题，明显这两个函数的图象对于直线t ＝ 0 对称，即函数 y＝ f(x－ 2)与 y＝ f(2－ x)的图象对于直线x－ 2＝ 0 即 x＝ 2 对称，故②正确；由 f(x＋ 2)＝－ f(x)，可得 f(x＋ 4)＝－ f(x＋ 2)＝ f(x)，我们只好获得函数的周期为4，即只好推得函数 y＝ f(x)的图象对于直线对称，故③错误；因为函数x＝ 4k(k∈ Z) 对称，不可以推得函数y＝ f(x)的图象对于直线x＝2f(x)为奇函数，且f(x)＝f(－ x－ 2)，可得f(－ x)＝ f(x＋ 2)，因为－x＋ x＋ 2＝ 1，可得函数 y＝ f(x)的图象对于直线x＝1对称，故④正确．211．设函数 f(x)是定义在 R 上的奇函数，且对随意实数x，恒有 f(x＋ 2)＝－ f(x)，当 x∈ [0,2]时， f(x)＝ 2x－ x2.(1)求证： f(x)是周期函数；(2)当 x∈[2,4] 时，求 f(x)的分析式；(3)计算 f(0)＋ f(1) ＋f(2)＋＋ f(2016) ．(1)证明∵ f(x＋ 2)＝－ f( x)，∴f(x＋ 4)＝－ f(x＋ 2)＝f(x)，∴f(x)是周期为 4 的周期函数．(2) 解∵ x∈ [2,4]，∴－ x∈ [ － 4，－ 2]，∴ 4－ x∈ [0,2] ，∴f(4－x)＝2(4－ x)－ (4－ x)2＝－ x2＋ 6x－ 8，又 f(4 －x)＝ f(－ x)＝－ f(x)，∴－ f(x)＝－ x2＋6x－ 8，即 f(x)＝ x2－ 6x＋8， x∈ [2,4] ．(3)解∵ f(0) ＝ 0， f(1)＝ 1， f(2) ＝ 0， f(3)＝－ 1，又 f(x)是周期为 4 的周期函数，∴ f(0)＋ f(1)＋ f(2) ＋ f(3)＝f(4)＋ f(5)＋ f(6) ＋ f(7)＝＝ f(2012) ＋ f(2013) ＋ f(2014) ＋ f(2015)＝0，∴ f(0)＋ f(1)＋ f(2) ＋＋ f(2016)＝f(2016) ＝f(0) ＝ 0.a12．已知函数f(x)＝ lg(x＋x－2) ，此中 a 是大于 0 的常数．【步步高】高考数学江苏(理)考前三个月配套练习：3.2函数性质与分段函数(含答案分析)(1)求函数 f(x)的定义域；(2)当 a∈ (1,4)时，求函数 f( x)在 [2，＋∞)上的最小值；(3)若对随意 x∈ [2，＋∞)，恒有 f(x)＞ 0，试确立 a 的取值范围．解 (1)由 x＋a－2＞ 0，得x2－2x＋ a＞ 0，x x当 a＞ 1时， x2－ 2x＋ a＞ 0 恒建立，定义域为(0，＋∞)；当 a＝ 1时，定义域为 { x|x＞ 0且 x≠1}；当 0＜ a＜1 时，定义域为 { x|0＜ x＜ 1－1－ a或 x＞ 1＋ 1－ a} ．a a＝x2－ a＞ 0 恒建立，(2) 设 g(x)＝ x＋－ 2，当 a∈ (1,4)， x∈[2，＋∞)时， g′(x)＝ 1－22x x xa因此 g(x)＝ x＋－2 在 [2，＋∞)上是增函数，因此 f( x)＝ lg x＋a－ 2在 [2，＋∞)上是增函数，xa－ 2在 [2，＋∞)上的最小值为f(2) ＝ lga因此 f( x)＝ lg x＋x2.a(3) 对随意 x∈ [2，＋∞)，恒有 f(x)＞ 0，即 x＋x－2＞ 1 对 x∈[2 ，＋∞)恒建立，因此 a＞ 3x－ x2对 x∈ [2，＋∞)恒建立．令 h(x) ＝3x－ x2，2329而 h(x) ＝3x－ x＝－x－2＋4在[2，＋∞)上是减函数，因此h(x)max＝ h(2) ＝ 2，因此 a＞ 2.。

训练26 三角函数(推荐时间：75分钟)1．已知sin α＝55，α∈(0，π2)，tan β＝13. (1)求tan α的值；(2)求tan (α＋2β)的值．2．在△ABC 中，角A 、B 、C 所对的边分别为a 、b 、c ，且1－c2a ＝B －CB ＋C，求 cos B2的值．3．若函数f (x )＝sin 2ax －sin ax cos ax (a ＞0)的图象与直线y ＝m (m 为常数)相切，并且切点的横坐标依次成公差为π2的等差数列．(1)求m 的值；(2)若点A (x 0，y 0)是y ＝f (x )图象的对称中心，且x 0∈[0，3π4]，求点A 的坐标．4.已知△ABC 的三个内角A 、B 、C 所对的边分别为a 、b 、c .m ＝(1,1)，n ＝⎝ ⎛⎭⎪⎫32－sin B sin C ，cos B cos C ，且m ⊥n . (1)求A 的大小；(2)若a ＝1，b ＝3c .求S △ABC .5．设函数f (x )＝2sin x cos2φ2＋cos x sin φ－sin x (0＜φ＜π)，在x ＝π处取最小值．(1)求φ的值；(2)在△ABC 中，a 、b 、c 分别是角A 、B 、C 的对边，已知a ＝1，b ＝2，f (A )＝32，求角C .6．(·福建)某港口O 要将一件重要物品用小艇送到一艘正在航行的轮船上，在小艇出发时，轮船位于港口O 北偏西30°且与该港口相距的A 处，并正以30海里/时的航行速度沿正东方向匀速行驶．假设该小艇沿直线方向以v 海里/时的航行速度匀速行驶，经过t 时与轮船相遇．(1)若希望相遇时小艇的航行距离最小，则小艇航行速度的大小应为多少？(2)假设小艇的最高航行速度只能达到30海里/时，试设计航行方案(即确定航行方向和航行速度的大小)，使得小艇能以最短时间与轮船相遇，并说明理由．答案1．解 (1)∵sin α＝55，α∈(0，π2)， ∴cos α＝1－sin 2α＝1－15＝255. ∴tan α＝sin αcos α＝55255＝12.(2)∵tan β＝13，∴tan 2β＝2tan β1－tan 2β＝2×131－132＝34. ∴tan (α＋2β)＝tan α＋tan 2β1－tan αtan 2β＝12＋341－12×34＝2.2．解 由已知得 2a －c2a ＝B －Csin A，∴2sin A －sin C2sin A＝B －Csin A，∴2sin A －sin C ＝2sin (B －C )， ∴2sin (B ＋C )－sin C ＝2sin (B －C )， 2sin B cos C ＋2cos B sin C －sin C ， ＝2sin B cos C －2cos B sin C ， ∴4cos B sin C ＝sin C ， 又sin C ≠0，∴cos B ＝14.B 为锐角．∴cos B2＝1＋cos B 2＝1043．解 (1)f (x )＝12(1－cos 2ax )－12sin 2ax＝－12(sin 2ax ＋cos 2ax )＋12＝－22sin (2ax ＋π4)＋12∵y ＝f (x )的图象与y ＝m 相切． ∴m 为f (x )的最大值或最小值． 即m ＝1＋22或m ＝1－22.(2)又因为切点横坐标依次成公差为π2的等差数列，所以f (x )最小正周期为π2.又T ＝2π|2a |＝π2，a ＞0，所以a ＝2. 即f (x )＝－22sin ⎝⎛⎭⎪⎫4x ＋π4＋12 令sin ⎝⎛⎭⎪⎫4x ＋π4＝0，则4x 0＋π4＝k π(k ∈Z )x 0＝k π4－π16.由0≤k π4－π16≤34π及k ∈Z . 得k ＝1,2,3，因此对称中心点A 的坐标为⎝ ⎛⎭⎪⎫316π，12、⎝ ⎛⎭⎪⎫716π，12、⎝ ⎛⎭⎪⎫1116π，12.4．解 因为m ⊥n ，所以32－sin B sin C ＋cos B cos C ＝0， 所以cos (B ＋C )＝－32，即cos A ＝32， 因为A 为△ABC 的内角，所以0<A <π， 所以A ＝π6.(2)若a ＝1，b ＝3c .由余弦定理得b 2＋c 2－a 2＝2bc cos A ，所以得c 2＝1，所以S △ABC ＝12bc ·sin A ＝34c 2＝34.5．解 (1)∵f (x )＝2sin x cos 2 φ2＋cos x sin φ－sin x＝2sin x ·1＋cos φ2＋cos x sin φ－sin x＝sin x ＋sin x cos φ＋cos x sin φ－sin x＝sin x cos φ＋cos x sin φ＝sin (x ＋φ) 又∵f (x )在x ＝π处取最小值． ∴sin (π＋φ)＝－1. 又∵0＜φ＜π，∴φ＝π2.(2)由(1)知f (x )＝sin (x ＋π2)＝cos x . ∵f (A )＝32，∴cos A ＝32. 又∵A 是三角形的内角，∴A ＝π6.又∵a ＝1，b ＝2，∴由正弦定理得sin B ＝b sin Aa＝2×121＝22. 又∵a ＜b ，∴B ＝π4或B ＝3π4，当B ＝π4时，C ＝7π12；当B ＝3π4时，C ＝π12.∴C ＝π12或7π12.6．解 方法一 (1)如图(1)，设相遇时小艇航行的距离为S 海里，则S ＝900t 2＋400－2×30t－＝900t 2－600t ＋400图(1)＝t －132＋300.故当t ＝13时，S min ＝103，此时v ＝10313＝30 3.即小艇以30 3 海里/时的速度航行，相遇时小艇的航行距离最小． (2)设小艇与轮船在B 处相遇，则v 2t 2＝400＋900t 2－2×0t ×cos(90°－30°)，故v 2＝900－600t ＋400t2.∵0<v ≤30，∴900－600t ＋400t2≤900，即2t 2－3t ≤0，解得t ≥23. 又t ＝23时，v ＝30.故v ＝30时，t 取得最小值，且最小值为23.此时，在△OAB 中，有OA ＝OB ＝AB ＝可设计航行方案如下：航行方向为北偏东30°，航行速度为30海里/时，小艇能以最短时间与轮船相遇．图(2)方法二 (1)若相遇时小艇的航行距离最小，又轮船沿正东方向匀速行驶，则小艇航行方向为正北方向．设小艇与轮船在C 处相遇(如图(2)．在Rt△OAC 中，OC ＝s 30°＝103，AC ＝n 30°＝10. 又AC ＝30t ，OC ＝vt .此时，轮船航行时间t ＝1030＝13，v ＝10313＝30 3.即小艇以30 3 海里/时的速度航行，相遇时小艇的航行距离最小．图(3)(2)猜想v ＝30时，小艇能以最短时间与轮船在D 处相遇，此时AD ＝DO ＝30t . 又∠OAD ＝60°，∴AD ＝DO ＝OA ＝解得t ＝23.据此可设计航行方案如下：航行方向为北偏东30°，航行速度的大小为30海里/时．这样，小艇能以最短时间与轮船相遇．证明如下：如图(3)，由(1)得OC ＝103，AC ＝10，故OC >AC ，且对于线段AC 上的任意点P ，有OP ≥OC >AC .而小艇的最高航行速度只能达到30海里/时，故小艇与轮船不可能在A ，C 之间(包含C )的任意位置相遇．设∠COD ＝θ(0°<θ<90°)，则在Rt△COD 中，CD ＝103tan θ，OD ＝103cos θ. 由于从出发到相遇，轮船与小艇所需要的时间分别为t ＝10＋103tan θ30和t ＝103v cos θ，∴10＋103tan θ30＝103v cos θ.由此可得，v ＝153θ＋. 又v ≤30，故sin(θ＋30°)≥32. 从而，30°≤θ＜90°.由于θ＝30°时，tan θ取得最小值，且最小值为33. 于是，当θ＝30°时，t ＝10＋103tan θ30取得最小值，且最小值为23.图(4)方法三 (1)同方法一或方法二．(2)设小艇与轮船在B 处相遇．依据题意得：v 2t 2＝400＋900t 2－2·0t ·cos(90°－30°)， (v 2－900)t 2＋600t －400＝0. ①若0<v <30，则由Δ＝360 000＋1 600(v 2－900) ＝1 600(v 2－675)≥0， 得v ≥15 3.从而，t ＝－300±20v 2－675v 2－900，v ∈[153，30)．当t ＝－300－20v 2－675v 2－900时，令x ＝v 2－675，则x ∈[0,15)，t ＝－300－20x x 2－225＝－20x －15≥43，当且仅当x ＝0，即v ＝153时等号成立． 当t ＝－300＋20v 2－675v 2－900时，同理可得23<t ≤43. 综上得，当v ∈[153，30)时，t >23.②若v ＝30，则t ＝23.综合①②可知，当v ＝30时，t 取最小值，且最小值等于23.此时，在△OAB 中，OA ＝OB ＝AB ＝可设计航行方案如下：航行方向为北偏东30°，航行速度为30海里/时，小艇能以最短时间与轮船相遇．。

专题限时集训(十)[第10讲 数列求和及数列应用](时间：10分钟＋35分钟)2012二轮精品提分必练1．等比数列{a n }首项与公比分别是复数i ＋2(i 是虚数单位)的实部与虚部，则数列{a n }的前10项的和为( )A ．20B ．210－1 C ．－20 D ．－2i2012二轮精品提分必练2012二轮精品提分必练1．设数列{a n }是等差数列，且a 2＝－8，a 15＝5，S n 是数列{a n }的前n 项和，则( ) A ．S 10＝S 11 B ．S 10>S 11 C ．S 9＝S 10 D ．S 9<S 10 2．等比数列{a n }的前n 项和为S n ，若S 1，S 3，S 2成等差数列，则{a n }的公比q 等于( )A ．1 B.12C ．－12D ．23．已知数列{a n }的通项公式a n ＝log 3nn ＋1(n ∈N *)，设其前n 项和为S n ，则使S n <－4成立的最小自然数n 等于( )A ．83B ．82C ．81D ．804．“神七升空，举国欢庆”，据科学计算，运载“神七”的“长征二号”F 火箭，在点火第一秒钟通过的路程为2 km ，以后每秒钟通过的路程都增加2 km ，在达到离地面240 km 的高度时，火箭与飞船分离，则这一过程需要的时间大约是( )A ．10秒钟B ．13秒钟C ．15秒钟D ．20秒钟5．过圆x 2－5x ＋y 2＝0内点P ⎝ ⎛⎭⎪⎫52，32有n 条弦，这n 条弦的长度依次成等差数列{a n }，其中最短弦长为a 1，最长的弦长为a n ，且公差d ∈⎝ ⎛⎭⎪⎫15，12，那么n 的取值集合为( ) A ．{5,6} B ．{4,5}C ．{3,4,5}D ．{3,4,5,6}6．{a n }为等差数列，若a 11a 10<－1，且它的前n 项和S n 有最大值，那么S n 取得最小正值时，n 的值为( )A ．11B ．17C ．19D ．217．已知数列{a n }的前n 项和S n ＝n 2＋2n －1，则a 1＋a 3＋a 5＋…＋a 25＝________.8．在计算“11×2＋12×3＋…＋1n n ＋(n ∈N *)”时，某同学学到了如下一种方法：先改写第k 项：1k k ＋＝1k －1k ＋1，由此得，11×2＝11－12，12×3＝12－13，…，1n n ＋＝1n －1n ＋1，相加，得11×2＋12×3＋…＋1n n ＋＝1－1n ＋1＝nn ＋1.类比上述方法，请你计算“11×2×3＋12×3×4＋…＋1n n ＋n ＋(n ∈N *)”，其结果为________________．9．已知以1为首项的数列{a n }满足：a n ＋1＝⎩⎪⎨⎪⎧a n ＋n 为奇数，a n2n 为偶数(n ∈N *)．(1)写出a 2，a 3，a 4，并求数列{a n }的通项公式；(2)设数列{a n }的前n 项和S n ，求数列{S n }的前n 项和T n .10．设数列{a n }满足：a 1＋2a 2＋3a 3＋…＋na n ＝2n (n ∈N *)． (1)求数列{a n }的通项公式；(2)设b n ＝n 2a n ，求数列{b n }的前n 项和S n .专题限时集训(十)【基础演练】1．A 【解析】 根据复数实部和虚部的概念求出这个等比数列的首项和公比，按照等比数列的求和公式进行计算．该等比数列的首项是2，公比是1，故其前10项之和是20.2．A 【解析】 由a n ＋1＝3S n ⇒S n ＋1－S n ＝3S n ⇒S n ＋1＝4S n ，所以数列{S n }是首项为1，公比为4的等比数列，所以S n ＝4n －1，所以a 6＝S 6－S 5＝45－44＝3×44，所以选择A.3．A 【解析】 a 1＋a 2＋…＋a 10＝－1＋4－7＋10＋…＋(－1)10·(3×10－2)＝(－1＋4)＋(－7＋10)＋…＋[(－1)9·(3×9－2)＋(－1)10·(3×10－2)]＝3×5＝15.故选A.4．D 【解析】 从实际问题中考虑将树苗放在最中间的坑旁边，则每个人所走的路程和最小，一共20个坑，为偶数，在中间的有两个坑为10和11号坑，故答案选D.【提升训练】1．C 【解析】 设公差为d ，则d ＝5＋815－2＝1，所以a n ＝n －10，因此S 9＝S 10是前n 项和中的最小值，选择C.2．C 【解析】 依题意，由2S 3＝S 1＋S 2得2(a 1＋a 1q ＋a 1q 2)＝a 1＋a 1＋a 1q ，解得q ＝－12，选择C.3．C 【解析】 S n ＝log 31－log 32＋log 32－log 33＋…＋log 3n －log 3(n ＋1)＝－log 3(n＋1)<－4，解得n >34－1＝80.4．C 【解析】 设每一秒钟通过的路程依次为a 1，a 2，a 3，…，a n ，则数列{a n }是首项a 1＝2，公差d ＝2的等差数列，由求和公式得na 1＋n n －d2＝240，即2n ＋n (n －1)＝240，解得n ＝15.故选C.5．B 【解析】 已知圆的圆心为Q ⎝ ⎛⎭⎪⎫52，0，半径r ＝52.又|PQ |＝32，∴a 1＝2r 2－|PQ |2＝4，a n ＝2r ＝5，∴d ＝a n －a 1n －1＝1n －1∈⎝ ⎛⎭⎪⎫15，12，∴n ∈(3,6)，∴n ＝4或n ＝5.6．C 【解析】 等差数列的前n 项和有最大值，则其公差为负值，数列单调递减，根据a 11a 10<－1可知一定是a 10>0，a 11<0，由此得a 11<－a 10，即a 11＋a 10<0，S 19＝a 1＋a 192×19＝19a 10>0，S 20＝a 1＋a 202×20<0，由于S n 在取得最大值后单调递减，根据已知S n 在[11，＋∞)上单调递减，所以使得S n 取得最小正值的n 值为19.7．350 【解析】 a n ＝⎩⎪⎨⎪⎧2，n ＝1，2n ＋1，n ≥2，所以a 1＋a 3＋a 5＋…＋a 25＝(a 1＋1)＋a 3＋a 5＋…＋a 25－1＝＋2×13－1＝350.8.n 2＋3n n ＋n ＋ 【解析】 裂项1n n ＋n ＋＝121n n ＋－1n ＋n ＋，相消得结果为n 2＋3n n ＋n ＋.9．【解答】 (1)a 2＝2，a 3＝1，a 4＝2，a n ＝3＋－n2.(2)S n ＝3n 2＋12·－－－n]2＝3n 2－14＋14(－1)n， ∴T n ＝32·n n ＋2－14n ＋14·－[1－－n]1＋1＝34n 2＋12n ＋18·(－1)n－18(也可分奇数和偶数讨论解决)． 10．【解答】 (1)∵a 1＋2a 2＋3a 3＋…＋na n ＝2n，①∴n ≥2时，a 1＋2a 2＋3a 3＋…＋(n －1)a n －1＝2n －1，② ①－②得na n ＝2n －1，a n ＝2n －1n(n ≥2)，在①中令n ＝1，得a 1＝2，∴a n ＝⎩⎪⎨⎪⎧n ＝，2n －1nn ，(2)∵b n ＝⎩⎪⎨⎪⎧n ＝，n ·2n －1n ，则当n ＝1时，S 1＝2；当n ≥2时，S n ＝2＋2×2＋3×22＋…＋n ·2n －1，③则2S n ＝4＋2×22＋3×23＋…＋(n －1)·2n －1＋n ·2n，④④－③得S n ＝n ·2n －(2＋22＋23＋…＋2n －1)＝(n －1)2n＋2(n ≥2)，又S 1＝2满足上式，∴S n ＝(n －1)·2n ＋2(n ∈N *)．。

训练4 不等式1．“a >0且b >0”是“a ＋b2≥ab ”成立的________条件．2．(2010·江西改编)对于实数a ，b ，c ，“a ＞b ”是“ac 2＞bc 2”的________条件． 3．若实数x ，y 满足1x 2＋1y2＝1，则x 2＋2y 2的最小值为________．4．不等式x 2－4>3|x |的解集是________．5．(2011·天津)已知集合A ＝{x ∈R ||x ＋3|＋|x －4|≤9}，B ＝{x ∈R |x ＝4t ＋1t－6，t ∈(0，＋∞)}，则集合A ∩B ＝________.6．已知p ：关于x 的不等式|x －2|＋|x ＋2|>m 的解集为R ；q ：关于x 的不等式x 2＋mx ＋4>0的解集为R .则p 成立是q 成立的________条件．7．设a ＞b ＞0，则a 2＋1ab ＋1a a －b的最小值是________．8．(2011·大纲全国)若变量x ，y 满足约束条件⎩⎪⎨⎪⎧x ＋y ≤6，x －3y ≤－2，x ≥1，则z ＝2x ＋3y 的最小值为________．9．已知关于x 的不等式组⎩⎪⎨⎪⎧x 2－x －2>0，2x 2＋k ＋x ＋5k <0的解集是M ，若M ∩Z ＝∅，则常数k的取值范围是________．10．若关于x 的不等式(a ＋b )x ＋2a －3b <0的解集是⎩⎨⎧⎭⎬⎫x |x <－13，则(a －3b )x ＋b －2a >0的解集是________．11．(2010·江苏)已知函数f (x )＝⎩⎪⎨⎪⎧x 2＋1，x ≥0，1，x <0，则满足不等式f (1－x 2)>f (2x )的x的取值范围是________．12．若不等式|3x －b |<4的解集中的整数有且仅有1,2,3，则b 的取值范围为________． 13．若关于x 的不等式(2x －1)2<ax 2的解集中整数恰好有3个，则实数a 的取值范围是__________．14．(2011·四川改编)某运输公司有12名驾驶员和19名工人，有8辆载重量为10吨的甲型卡车和7辆载重量为6吨的乙型卡车．某天需送往A 地至少72吨的货物，派用的每辆车需满载且只运送一次，派用的每辆甲型卡车需配2名工人，运送一次可得利润450元；派用的每辆乙型卡车需配1名工人，运送一次可得利润350元．该公司合理计划当天派用两类卡车的车辆数，可得最大利润为________．答案1．充分不必要 2．必要不充分 3．3＋2 2 4．(－∞，－4)∪(4，＋∞) 5．{x |－2≤x ≤5} 6．必要不充分 7．4 8．5 9．2≤k ≤310．{x |x <－3} 11．(－1，2－1) 12．5<b <7 13.⎝ ⎛⎦⎥⎤259，4916 14．4 900元。

二.函数与导数 高频考点整合 函数单调性：若0（X ）MO, /（ r ）为增函 数；若（x ）WO /（；）为减函数 〔（1）求导数.＜（；£） （2） 求方程f 3=0的根 （3） 检查/（ Q 在方程根左右的 值的符号，女口果左正右负，那 么「（」：）取得极大值；如果左 负右正，那么f （.Q 取得极小值函数在闭区间上的最值：将在区间内取得的极值与边界值比较，得到最值映射T 函数图象 常见函数的图象 函数图象的变换 概念 函数的定义 导数的概念: 导数的几何意义 基本导数公式 导数的运算 两个函数和、差、积、商的导数 复合函数的导数 导数的 应基础回扣训练1.已知函数/(x)=^=+(x-l)°的定义域为M,g(x)=ln (2 —x)的定义域为N,则出门"={刘一2<丫<2 IlxHl} .解析由函数—c== +(X - 1)°有意义可知，2 +x>0 \]2+ x且X - 1H0, M=[x\x> -2,且力工1}；同理N= {xlv<2}. :.MQN= {x\-2<x<2且xHl}.2.曲线y = e条在点(4, e?)处的切线与坐标轴所围三角形的面积为e? .解析・・・f (心昇"，・・・曲线在点(4, e?)处的切线的斜率为£=f (4)=芬,切线方程为y- e2 =^e2(x- 4),即^e2x-y-e2 = 0,切线与兀轴和y轴的交点坐标分别为A(2,0)、3(0, -e2),则切线与坐标轴围成的三角形043 的面积为^X2Xe2 = e2.3.定义在R上的函数/（x）既是奇函数，又是周期函数，T 是它的一个正周期.若将方程/（兀）=0在闭区间［一八T］上的根的个数记为小则〃至少为5 •解析由于/U）是R上的奇函数，则夬0） = 0.又yu）是以丁为周期的周期函数，则=/（o）=x-n = o.头為=4. ____________________________________________ 幕函数当。