下载文档原格式
几何非线性力学中的定解问题研究几何非线性力学是以物体的形状和变形为主要研究对象，涉及到多个学科的交叉，如数学、力学、材料科学等。
其中，定解问题是研究重要的方向之一。
本文旨在简要介绍几何非线性力学中的定解问题研究。
一、定解问题概述定解问题是研究微分方程的重要领域，从物理学的角度来讲，定解问题是描述力学系统的运动规律，因此在几何非线性力学中，定解问题也是研究物体受力时的变形与运动规律的重要工具。
在几何非线性力学中，一般研究以下两类定解问题：1.初值问题初值问题是指在某一时刻，物体的形状与位置已知，要求预测在后续时间内的形状和位置的变化情况。
这类问题通常用泰勒级数来进行近似求解，但是要求计算过程中不受舍入误差的影响，也需要对误差进行估计和控制。
2.边值问题边值问题是指在一个密闭区域内，物体受到一定约束力的情况下，求解物体的形状与运动规律。
这类问题通常需要建立较为复杂的数学模型，涉及到微分方程、变分原理等多种数学工具。
二、定解问题的数学模型与求解方法几何非线性力学中的定解问题，有时需要建立复杂的非线性微分方程，因此需要借助于数值计算方法来进行求解。
目前常用的数值计算方法有以下几类：1.差分法差分法是一种离散化求解微分方程的方法，将空间和时间分为若干个网格，根据物体的受力情况，利用有限差分法来逼近微分方程的解。
这种方法简单易行，在一些简单的模型中表现良好。
2.有限元法有限元法是一种将物体分割成有限个单元，建立每个单元的形状函数和位移函数，从而建立起整个物体的数学模型。
这种方法具有一定的通用性，在处理非线性问题时有很好的效果。
3.辛普森法辛普森法是一种以积分为基础的数值计算方法，通过对微分方程的积分逼近来求解方程的解。
辛普森法具有高精度和高效率的特点，但在处理非线性问题时，需要对误差进行较为精细的控制。
三、应用与展望几何非线性力学中的定解问题广泛应用于材料科学、工程力学、地质力学等各个领域，在地震预测、纳米器件设计等领域具有重要的应用价值。
非线性力学问题的求解研究引言随着科技的发展和人类对自然规律的深入探索，研究非线性力学问题的重要性日益凸显。
非线性力学问题的求解研究，是指对非线性物理系统进行建模和计算，以确定其动力学特性、稳定性和响应。
本文将介绍非线性力学问题的求解方法和研究现状。
一、非线性力学问题的简介非线性力学问题是指系统动力学方程中包含非线性项的问题。
最常见的非线性方程是二次方程、三次方程、指数方程等。
非线性问题通常较为复杂，其解析解常难以求得，一般需要采用数值计算方法或近似方法来求解。
非线性力学问题可以涉及多个学科领域，如物理学、数学、工程学等。
在物理学中，非线性问题的出现常常与热力学、流体力学、固体力学等领域密不可分。
同时，非线性物理系统的性质和现象也是各学科的热点研究方向，例如地震学、气象学、生物学等。
二、非线性力学问题的求解方法1. 数值计算方法数值计算方法是求解非线性力学问题最常用的方法之一。
该方法将非线性方程转化为数字表示，采用数值逼近和迭代计算的方式求解。
常见的数值计算方法包括有限差分法、有限元方法、边界元方法等。
有限差分法通过对函数在有限步长上的差分近似，将微积分方程转化为代数方程，在计算机上实现数值计算。
有限元方法则通过对物理体系的分割，并在分割区域上建立简化模型，将物理问题转换为数学问题，通过求解矩阵方程得到数值计算解。
边界元方法是一种求解偏微分方程的数值计算方法。
该方法将偏微分方程转化为边界上的积分方程，通过迭代计算逼近方程解。
2. 近似方法非线性方程解析解难以求得，因此近似方法成为另一种常用的求解方法。
近似方法是将非线性方程进行逼近或拟合，以得到近似解。
常见的近似方法包括变分法、微扰法、双曲正切方法等。
变分法是一种优化问题的数学方法。
它将问题转化为优化问题，通过最小化泛函来求解方程解或波函数的近似解。
微扰法是将非线性方程进行分解，采用初值近似解来进行迭代求解的方法。
双曲正切方法是一种通过非线性函数的双曲正切函数逼近进行求解的方法。
固体力学非线性课程报告一、结构非线性载荷与变形曲线之间呈非线性的关系，也即显示了非线性结构的基本特征—变化的结构钢性。
引起结构非线性变化的原因有很多，主要是三种类型：1）状态变化（包括接触）；许多普通的结构表现出一种与状态有关的非线性行为，如电缆的松弛与紧绷，轴套的接触与非接触，这些系统的结构刚度都是由于状态的改变而突然变化。
状态的改变可能和载荷有关，也可能与某种外部原因有关。
其中接触问题很典型，它的特点是：属于边界非线性问题，边界条件不在是定解条件，而是待求结果，两接触体之间的接触面积与压力随外载荷的变化而变化，并且与接触体的刚性有关。
其中接触模式可以分为三类：点对点，点对面，面对面。
目前对这类问题的求解主要是引用经典理论，借助有限元数值方法进行研究。
2）几何非线性几何非线性就是位移与应变呈非线性（微分)关系,这是因为在几何非线性条件下，物体或结构会发生较大的位移或转动（也叫有限变形），此时不同时刻的物体具有差别不能忽略的不同构型，其单元刚度矩阵会发生改变或者是单刚阵在向总刚阵变换时发生改变，它的位移的导数的二次项不能忽略。
对于大变形问题，连续介质力学理论对经历大变形后的变形，依据不同的参考对象（初始构型与现时构型）有严格的定义，在此基础上定义的应变有两种：格林应变张量（以初始构型为参考），它是客观的、不随刚体转动而变换的对称张量；另一种为阿尔曼斯应变张量（以现时构型为参考）在大变形分析中经常用到它们的增量形式，均有线性部分和非线性部分构成。
3）材料非线性应力与应变之间呈现非线性的关系。
材料的非线性行为异常丰富，有非线性弹性行为，塑性行为，粘弹性行为。
非线性弹性行为：当材料由于应力达到某种临界值而出现应力与应变间的非线性变化关系；塑性行为：当物体由于载荷超过某个临界值（弹性极限）而产生的永久变形，即有不可恢复的应变产生；粘弹性行为（包括松弛和蠕变）：具有介于弹性和黏性液体之间的材料性质，其形变不仅和当时作用力的大小有关，而且和温度的改变、力的作用时间以及加载历史都有关，同时应变速率、应力速率对应变也有影响。
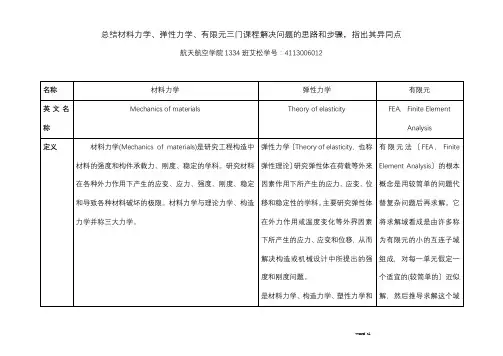
总结材料力学、弹性力学、有限元三门课程解决问题的思路和步骤，指出其异同点航天航空学院1334班艾松学号：4113006012线性关系，这类问题称为几何非线性问题。
③物理非线性问题。
在这类问题中，材料内的变形和内力之间〔如应变和应力之间〕不满足线性关系，即材料不服从胡克定律。
在几何非线性问题和物理非线性问题中，叠加原理失效。
解决这类问题可利用卡氏第一定理、克罗蒂－恩盖塞定理或采用单位载荷法等。
在许多工程构造中，杆件往往在复杂载荷的作用或复杂环境的影响下发生破坏。
例如，杆件在交变载荷作用下发生疲劳破坏,在高温恒载条件下因蠕变而破坏,或受高速动载荷的冲击而破坏等。
这些破坏是使机械和工程构造丧失工作能力的主要原因。
所以，材料力学还研究材料的疲劳性能、蠕变性能和冲击性能。
材料力学根本公式〔解决问题方法〕： 一、应力与强度条件 拉压：[]σσ≤=maxmax AN平衡微分方程〔1〕几何方程〔2〕物理方程〔3〕成由各变量或其导数的节点值与所选用的插值函数组成的线性表达式，借助于变分原理或加权余量法，将微分方程离散求解。
采用不同的权函数和插值函数形式，便构成不同的有限元方法。
有限元方法最早应用于构造力学，后来随着计算机的开展慢慢用于流体力学的数值模拟。
在有限元方法中，把计算域离散剖分为有限个互不重叠且相互连接的单元，在每个剪切：[]ττ≤=AQ max挤压：[]挤压挤压挤压σσ≤=AP圆轴扭转：[]ττ≤=W tTmax 平面弯曲： ①[]σσ≤=maxzmax W M②[]max t max t maxmax σσ≤=y I M z t max c max maxy I Mzc =σ[]cnax σ≤ ③[]ττ≤⋅=bI S Q z *max z max max斜弯曲：[]σσ≤+=maxyyz z max W M W M拉〔压〕弯组合：[]σσ≤+=maxmax zW MA N[]t max t z max t σσ≤+=y I M A N z []c max c z z max c σσ≤-=ANy I M 圆轴弯扭组合： ① 第三强度理论[]στσσ≤+=+=z2n2w2n 2w r34W M M(1)式中的σx 、σy 、σz 、τyz=τzy 、τxz=τzx 、τxy=τyx 为应力分量，X 、Y 、Z 为单位体积的体力在三个坐标方向的分量；(2)式中的u 、v 、w 为位移矢量的三个分量〔简称位移分量〕，εx 、εy 、εz 、γyz 、γxz 、γxy 为应变分量；(3)式中的E 和v 分别表示杨氏弹性模量和泊松比。
固体力学中的非线性问题与分岔的开题报告摘要：固体力学中的非线性问题与分岔是当前研究热点之一，本文主要介绍了非线性问题与分岔的概念、应用领域及其重要性，以及常见的数学方法和数值模拟方法，最后提出了未来的研究方向和建议。
1.引言固体力学是研究固体物体的形变、应力、应变和能量变化等基本规律的学科，具有广泛的理论基础和应用价值。
然而，在材料、结构和装备的设计和使用过程中，往往会遇到非线性问题和分岔现象的挑战，导致其力学性能难以预测和控制，因此非线性问题和分岔的研究具有重要的理论和实践意义。
2.非线性问题与分岔的概念及应用领域非线性问题指的是当系统的输入或输出变化超过某个临界值时，系统的响应不再是线性的，而是表现出明显的非线性特征。
分岔是指系统中的某些参数改变时，稳态解的数量或性质发生改变的现象。
非线性问题和分岔通常会导致电力系统失稳、材料强度降低、结构破坏等问题。
在工程实践中，非线性问题和分岔的应用领域非常广泛，例如在材料工程中，非线性问题和分岔对于材料的疲劳寿命和塑性变形行为的预测和控制具有重要的意义；在结构工程中，非线性问题和分岔对于结构的稳定性、屈曲承载力以及振动特性的分析和设计也具有重要的作用。
3.常用数学方法和数值模拟方法常用的数学方法包括：分岔理论、幂函数展开法、双曲正切法等。
其中，分岔理论是研究分岔现象及其机制的基本方法，它将系统的稳态解的数量和质量建立在系统参数的单值函数关系上，从而得到分岔形成和稳定性的解析表达式。
幂函数展开法和双曲正切法则是处理非线性微分方程的一种有效方法，能够求得系统的某些特殊解。
数值模拟方法包括：有限元法、边界元法、网格方法、蒙特卡罗方法等。
其中，有限元方法是一种数值求解偏微分方程的常用方法，适用于任意复杂的结构体系，能够精确得出结构的应力、变形和稳定性等信息。
边界元方法则是一种针对边界值问题的数值求解方法，能够求解出系统表面的应力和位移分布等信息。
4.未来的研究方向和建议未来的研究方向和建议包括：(1)开展材料的非线性力学实验研究，加深对材料非线性变形及其与强度之间本质联系的理解。
细观尺度下应变率对单晶铜动态力学行为的影响柳占立由小川庄茁1)(清华大学航天航空学院工程力学系，北京 100084)本文发展了一个耦合连续介质有限元与离散位错动力学的多尺度方法，并运用该方法研究了细观尺度下单晶铜动态力学行为。
一方面，基于位错滑移的离散位错动力学程序计算动态变形中的塑性变形，以代替常规有限元计算中使用的本构关系；另一方面，通过FE程序计算动态变形中的位移场和应力场。
我们把该多尺度框架以用户子程序的形式植入到Abaqus/Standard中。
在该框架下，我们研究了动态变形中加载速率对单晶铜屈服强度及位错微结构形态的影响。
随着应变率的提高，单晶铜的屈服强度迅速提高，并且对给定尺寸和初始位错源的单晶铜，存在一个临界应变率，低于这个临界应变率时，屈服强度将对应变率相对不太敏感。
随应变率的增加，位错图案从非均一化向均一化转变，并且集中在某个滑移系内，形成滑移带的形式。
滑移带内部的剪应力明显高于外部区域，变形带的宽度随应变率的增加而增加，它们往往是进一步发生破坏的位置。
关键词多尺度，位错动力学，变形带，流动应力车身外覆盖件表面缺陷产生机理的仿真研究2)付争春*郑国君*胡平+，3)*(吉林大学汽车动态模拟国家重点实验室车身与模具工程研究所，长春 130025)+(大连理工大学汽车工程学院，大连 116024)剧烈的市场竞争驱使汽车制造商从各方面来设法提高其轿车质量，轿车的“A”级表面（即车身外覆盖件的暴露面）要求一辆车的整个外观必须是光洁无瑕的。
然而，像模具压痕、拉延线、滑移线、松料、凹陷、畸变等缺陷在制造过程中会常常出现在“A”级表面上。
为了消除这些缺陷，就要费时耗资来返修模具或者需要手工精修这些覆盖件。
在轿车的“A”级表面上表面凹陷和畸变是两类主要的表面缺陷。
基于板料成形仿真分析软件KMAS/incremental，结合KMAS/Spring-back，首先研究了在车身外覆盖件成形时，在“A”级表面和特征形状区域不产生大的缺陷（如起皱和破裂）所需特征形状的尺寸变量，在此基础上深入研究了几种特征形状的不同尺寸变量与表面凹陷、畸变这两种缺陷的几何关系，分析了表面凹陷和畸变这两类缺陷产生的机理。
两种拉格朗日法T.L和U.L.几何非线性计算对比分析作者：张凯庆李永刘张璇赖建聪来源：《科技创新与应用》2016年第19期摘要：文章针对材料几何非线性特性，选取周边固支受均布载荷作用的圆板，分别利用两种拉格朗日法T.L和U.L.进行计算，最后进行对比分析。
通过对比发现，两种计算方法相差很小。
关键词：几何非线性拉格朗日法；TL法；UL法1 计算工况周边固支受均布载荷作用的圆板，其几何参数为：R=50.0cm，h=1cm，E=2.0E6kg/cm2（或2.56E6kg/cm2），v=0.3，？滓s=17.32kg/cm2，圆板大挠度理论解公式：wc/h+A（wc/h）3=Bq（a/h）4/E，将计算模型划分为15个单元，按15个等增量步计算中心点的载荷-位移曲线。
2 数值解计算与对比划分模型如图1所示。
单元划分及节点信息单元划分：径向划分15个8结点等参单元；结点总数：78；R向位移约束数：6；Z向位移约束数：3；均布力数：15。
边界条件：上边界作用均布力15；下边界自由；左边界简支；右边界固支根据几何非线性程序计算，可以得到TL和UL两种方法的中心点载荷位移曲线。
TL法结果如表1所示，UL方法结果如表2所示。
两种方法所得到的位移曲线比较如图2所示。
参考文献[1]李元媛，淡勇，蔡睿贤.理想塑性轴对称平面问题的解析解[J].机械工程学报，2009，7：270-273+277.[2]张年文，童根树.平面框架几何非线性分析的修正拉格朗日-协同转动联合法[J].工程力学，2009，8：100-106+130.[3]J.E.Barradas Cardoso，Nuno M.B. Benedito，Aníbal J.J. Valido.考虑翘曲变形的复合材料叠合梁几何非线性的有限元分析[J].钢结构，2009，10：82-83.[4]周凌远，李乔.基于UL法的CR列式三维梁单元计算方法[J].西南交通大学学报，2006，6：690-695.。
