第9章 系综理论
- 格式:ppt
- 大小:524.50 KB
- 文档页数:34





热力学中的双状态系统与系综理论在物理学中,热力学是研究温度和能量转移的学科。
它主要关注系统和它的环境之间的热力学关系。
热力学中的双状态系统与系综理论是热力学的基础之一。
热力学中的双状态系统指的是具有两个状态的物理系统。
在这两种状态之间,它们的热力学性质有所不同。
最常见的双状态系统是衣架,衣架上可以悬挂衣物,也可以没有衣物。
当衣物悬挂在衣架上时,衣架的能量会发生变化,因此它的热力学性质也会发生变化。
热力学中的双状态系统可以通过系综理论来描述。
系综理论是热力学中的一种理论,用于研究大量处于同一温度下的分子系统。
系综理论主要包括三个概念:微正则系综,正则系综和巨正则系综。
微正则系综是一种系统,它的能量、体积和粒子数都是固定的。
这种系综是一种封闭的系统,它的能量是恒定的,因为不与外界发生热交换。
微正则系综的特点是各状态的概率是等价的。
正则系综是一种系统,它的体积和粒子数是恒定的,而能量可以发生变化。
正则系综是一种开放的系统,能够与外界交换热量。
由于能量可以变化,因此它们可以在不同的能量状态下存在。
正则系综的特点是各状态的概率取决于体系的能量和温度,通常是玻尔兹曼分布。
巨正则系综是一种系统,它的能量、体积和粒子数都可以变化。
巨正则系综是一种对数系综,它描述的是粒子数与能量的关系。
巨正则系综的特点是各状态的概率取决于体系的化学势、温度和粒子数。
热力学中的双状态系统可以通过这些系综理论来研究。
对于双状态系统,微正则系综通常用于描述它们在两种状态之间的变化。
而对于更复杂的系统,如分子系统,正则系综和巨正则系综则更为适用。
总之,热力学中的双状态系统与系综理论在研究热力学基本问题和一些物理问题中都有着重要的意义。
通过深入了解这些理论,我们可以更好地理解物理学,同时也可以将它应用于生产和生活中的一些实际问题中。



课程设计题目:系综理论的讨论及运用学院:电子与信息工程学院专业:物理学师范姓名:学号:指导老师: 时间: 系综理论的讨论及运用姓名:摘要系综是处在相同的给定宏观条件下的大量结构完全相同的系统的集合。
它是统计物理的一个想象中的工具,而不是实际客体。
本文从概念开始讨论系综理论内容和运用。
关键词概念;系综理论;正则分布;关系;运用系综理论的基本观点是,宏观量是相应微观量的时间平均,而时间平均等价于系综平均。
系综的一个基本假设是各态历经假说:只要等待足够长的时间,宏观系统必将经历和宏观约束相应的所有可达微观态。
1 概念系统的一种可能的运动状态,可用相与中的一个相点表示,随着时间的推移,系统的运动状态改变了,相应的相点在相宇中运动,描绘出一条轨迹,由大量系统构成的系综则可表为相宇中大量相点的集合,随着时间的推移,各个相点分别沿各自的轨迹运动,类似于流体的流动。
若系统具有s个自由度,则相宇是以s个广义坐标p (详写为p、p2 ••…ps)和s个广义动量q(详写为q1、q2 ••…qs)为直角坐标构成的2s 维空间。
在相宇内任一点(p,q )附近单位相体积元内的相点数目D (p , q ,t )称为密度函数。
D(p,q,t)在整个相宇的积分等于全部相点数,即等于系综所包含的全部系统数N ,与时间t无关。
定义P p,q,t)=D(p,q,t)/N ,称为系综的概率密度函数。
P(p ,q, t) dpdq表示在t时刻出现在(p, q)点附近相体积元dpdq 内的相点数在全部相点数中所占的比值,即表示任一系统在t 时刻其运动状态处于(p,q )附近的相体积元dpdq内的概率。
显然,概率密度函数p( p, q , t)满足归一化条件/p(p,q,t ) dpdq=1 。
统计物理学的认为系统的任意宏观量I (t)是相应微观量L (p , q )在一定宏观条件下对系统一切可能的微观运动状态的统计平均值,即I(t )=几(p , q) p(p , q , t) dpdq。

第一章概念1.系统:孤立系统、闭系、开系与其他物体既没有物质交换也没有能量交换的系统称为孤立系;与外界没有物质交换,但有能量交换的系统称为闭系;与外界既有物质交换,又有能量交换的系统称为开系;2.平衡态平衡态的特点:1.系统的各种宏观性质都不随时间变化;2。
热力学的平衡状态是一种动的平衡,常称为热动平衡;3.在平衡状态下,系统宏观物理量的数值仍会发生或大或小的涨落;4.对于非孤立系,可以把系统与外界合起来看做一个复合的孤立系统,根据孤立系统平衡状态的概念推断系统是否处在平衡状态.3.准静态过程和非准静态过程准静态过程:进行得非常缓慢的过程,系统在过程汇总经历的每一个状态都可以看做平衡态。
非准静态过程,系统的平衡态受到破坏4.内能、焓和熵内能是状态函数.当系统的初态A和终态B给定后,内能之差就有确定值,与系统由A到达B所经历的过程无关;表示在等压过程中系统从外界吸收的热量等于态函数焓的增加值。
这是态函数焓的重要特性克劳修斯引进态函数熵.定义:5.热容量:等容热容量和等压热容量及比值定容热容量:定压热容量:6.循环过程和卡诺循环循环过程(简称循环):如果一系统由某个状态出发,经过任意一系列过程,最后回到原来的状态,这样的过程称为循环过程。
系统经历一个循环后,其内能不变。
理想气体卡诺循环是以理想气体为工作物质、由两个等温过程和两个绝热过程构成的可逆循环过程。
7.可逆过程和不可逆过程不可逆过程:如果一个过程发生后,不论用任何曲折复杂的方法都不可能使它产生的后果完全消除而使一切恢复原状。
可逆过程:如果一个过程发生后,它所产生的后果可以完全消除而令一切恢复原状.8.自由能:F和G定义态函数:自由能F,F=U-TS定义态函数:吉布斯函数G,G=U-TS+PV,可得GA-GB-W1定律及推论1.热力学第零定律-温标如果物体A和物体B各自与外在同一状态的物体C达到热平衡,若令A与B进行热接触,它们也将处在热平衡.三要素:(1)选择测温质;(2)选取固定点;(3)测温质的性质与温度的关系。

《 热力学统计物理》复习提纲21、考试时间:120分钟2、考试题型有:简答题、单项选择题、填空题、计算题、证明题、(或判断题)3、分数分布:25、20、25、18、12/124、复习思考题0、重点和难点:(六)近独立粒子的最概然分布:粒子运动状态的经典描述,量子描述,系统微观运动状态,三种分布。
(6学时)重点:三种分布。
难点:系统微观运动状态。
(七)Boltzman 统计:热力学量的统计表达式,理想气体的物态方程,Maxwell 速度分布律,能量均分定理。
(6学时)重点:热力学量的统计表达式。
难点:Maxwell 速度分布律。
(八)Bose 和Fermi 统计:热力学量的统计表达式。
(2学时)重点:热力学量的统计表达式。
(九)系综理论:相空间,Liuvil 定理,微正则分布,微正则分布的热力学公式,正则分布,正则分布的热力学公式,巨正则分布,热力学公式。
(8学时)重点:微正则、正则和巨正则分布热力学公式。
难点:相空间。
(十)涨落理论:涨落的准热力学理论。
(2学时)重点:涨落的准热力学理论。
难点:布朗运动。
一、填空题1、根据费米分布,温度为T 时处在能量为ε的一个量子态上的平均电子数为 。
2、若过程进行的每一中间态都是平衡态,则此过程称为 过程。
3、最大功定理指的是 。
4、盐的水溶液、水蒸气和冰三相平衡共存时,=ϕ ,=f ,溶液的冰点和饱和蒸气压都取决于盐的浓度x5、理想玻色气体出现凝聚的临界条件为 。
6、盐的水溶液与水蒸气平衡时,=ϕ ;=f ,水蒸气的饱和蒸气压随温度和盐的浓度而变,说明只有温度T 和浓度x 两个独立变量。
7、双原子分子能量中,如果有五个平方项,当温度为T 时,则分子数为N 的双原子分子理想气体的内能=U ;定压热容量=p C 。
9、粒子在三维空间运动,它的自由度为 ,粒子的质量为m ,粒子在任一时刻运动的动量为xm p x =,y m p y =,z m p z =,则此自由粒子的动能:=ε 。
第三章统计系综3.1 引言宏观性质B 应是系统辗转经历各种微观态时所表现的该性质的时间平均值。
∫=τττ0),(1d p r B B i i Gibbs 系综方法:系统性质对时间的平均等价于大量标本系统性质的平均。
这些标本系统的集合称之为系综(ensemble)。
r i (t ), p i (t ) 为质点的坐标和动量i = 1, 2, 3…N (~1024)需知,,6N 个一阶微分方程。
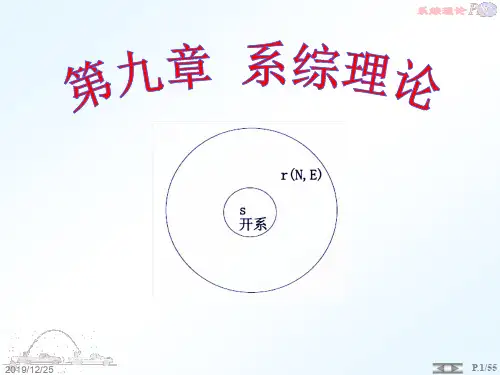
dtdp dt dr ii ,3.2 正则系综一、正则系综定义:若有一个体积为V,粒子数为N的热力学系统,置于一温度为T的大热浴中(保持恒温),为计算这个恒温封闭系统的热力学性质,需设计一个如下图的系综。
T, V, N指定的标本系统将大量(数目为)的体积为V,粒子N数为N,温度为T的标本系统堆积在一起,这些标本系统之间有导热壁隔开,可以彼此传递热量但不许粒子通过,这样的样本系统集合称之为正则系综,系综由绝热壁所包围。
一、正则分布EE n N n ii i ==∑∑(1)(2)设这些标本体系能够取得的能量状态为:E 1,, E 2,, E 3,,…E i …处于各能量状态(即量子态,包括了简并度)的相应体系数目为:n 1 ,n 2, n 3, …n i …设整个系综的总能量为E ,则限制条件为:由于系综中每一个标本系统彼此可以辨别,所以给出系综的一个分布n 1 ,n 2, n 3, …n i …的排列方法数-即系综的微观状态数Ω为:)!!...!/(!21i n n n N =Ω举例说明上式:abcd箱2bcd acd abd abc 箱14321排列序号共4种,即:4!1!3/!4==Ω(3)将a ,b ,c ,d 四个粒子放入两个箱中的方法各种各样,现求出n 1 = 3, n 2= 1这种方法的数目:(3)式可产生各种分布{n i },当最可几分布时,愈易出现Ωn i * n i(3)式两边首先取对数,并应用Stirling 公式,ln !ln ,ln ln ln i iiN N N N N N n n =−Ω=−∑则(5)则Ω或ln Ω应为极值(4)ln ln i i i i i i in n n n ⎛⎞⎛⎞=−⎜⎟⎜⎟⎝⎠⎝⎠∑∑∑由式(1)与(2)可知,求最可几分布问题是一个求条件极值问题,按照求条件极值的拉格朗日(Lagrange)未定乘数法将式(1)左端乘以因子-α,式(2)左端乘以因子-β,再与式(5)相加,最后对n i 求导可得:ln 0,1,2i i i i i i n n E i n αβ∂⎛⎞Ω−−==⎜⎟∂⎝⎠∑∑Lln ln 0i i i i i i i i i i i i in n n n n n E n αβ⎛⎞∂⎛⎞⎛⎞−−−=⎜⎟⎜⎟⎜⎟∂⎝⎠⎝⎠⎝⎠∑∑∑∑∑ln 1ln 10i i i i n n E αβ⎡⎤⎛⎞+−−−−=⎢⎥⎜⎟⎝⎠⎣⎦∑(6)(7)(8)iE i i i ee N n E n N βαβα−−=∴=−−−0ln ln (10)将式(10)代入式(1)中,可消去α,得:∑−=iE iee βα(11)∑−−=iE E i iiee N n ββ(12)∑−−==iE E i i iiee Nn p ββ(13)(9)∴式(10)变为:∴一个体系取能量状态E i 的几率为:即亦称状态和)(),,(∑−=iE ieN V T Z β(14)∑==iii p E E U (15)N i i iii V E P P p P P ⎟⎠⎞⎜⎝⎛∂∂−===∑(17)三、正则配分函数定义正则配分函数Z 为:下面求β的意义:由前述的力学量的时间平均等于系综平均的假定,热力学中的内能相当于系综的平均能量<E>,即压力对于压力来说,(16)将式(15)微分:i i i i i ii ii i i i i i i N i i idU d E p E dp p dE E E dp p dVV E dp P dV⎛⎞==+⎜⎟⎝⎠∂⎛⎞=+⎜⎟∂⎝⎠=−∑∑∑∑∑∑(18)与(19)对比得:∑=iii dp E S Td (19)(20)(18)dU Td S P dV=−Q把(21)代入式(20)中,得:()Z p E Z E p i i i i ln ln 1ln ln +−=∴−−=ββ(21)()()∑∑+−=+−=ii i i ii iZdp dp p dp Z p S Td ln ln 1ln ln 1ββ(22)将式(13)取对数得:由(23)式可见,β与热力学温度T成反比⎟⎠⎞⎜⎝⎛−=−=∴=∴=∑∑∑∑i i i iiiii i p p d dp p S Td dp p ln 1ln 11(1iββ),几率和为ΘkT1=β∑−=∴ikTE i eZ /(23)(24)k 为比例常数,即Boltamann 常数3.2正则配分函数与热力学函数的关系()/ln ln /ln ln i E kTi i i iii i i iiS k p p k p eZ p E Uk p Z k k Z kT T−=−=−=+=+∑∑∑∑(26)(27)/ln /−∂⎛⎞===⎜⎟∂⎝⎠∑∑2i E kTi i i iiVZ U E p E eZ kT T 由式(23)得:由式(15)得:,,ln T V T VF Z kT N N μ∂∂⎛⎞⎛⎞==−⎜⎟⎜⎟∂∂⎝⎠⎝⎠(29)(30)ln F U TS kT Z=−=−ln T TF Z P kT V V ∂∂⎛⎞⎛⎞=−=⎜⎟⎜⎟∂∂⎝⎠⎝⎠(28)作业:已知VDW 方程:求范德华型配分函数。
理论物理专业硕士研究生培养方案一、培养目标培养符合国家建设需要, 为祖国和人民服务的, 具有良好道德品质和科学素质的, 具有集体主义精神, 实事求是, 追求真理, 献身科学教育事业的, 具有扎实基础知识和良好科研能力的理论物理专门人才和高等院校师资.获得本专业硕士学位的研究生应掌握理论物理学科坚实、宽厚的基础知识,较全面和深入的专业知识,熟悉本专业研究方向的发展前沿和热点. 硕士论文选题时,应对国内外研究现状进行较全面的调研和分析,在此基础上,完成具有创造性的研究成果。
熟练掌握一门外语, 包括专业阅读和写作,以及能用外语进行简单的学术交流。
二、本专业总体概况、优势与特色理论物理是研究物质结构、性质及其相互作用的基本规律的一门基础学科。
本学科于1990年获得硕士学位授予权,1996年成为湖南省重点学科,1999年其中的“非线性物理”成为“211工程”重点学科,1995年起招收博士生,2000年获得博士学位授予权。
该学科现已形成四个稳定的研究方向。
其特色在于抓住当前和未来高技术领域中的关键问题和物理学中的基本问题开展基础研究,把基础研究与高技术问题的探索相结合,在多个学科前沿领域的交叉点寻找突破。
三、本专业研究方向及简介本学科分四个方向,方向一:光与物质的的相互作用物理。
方向二:原子分子理论。
方向三:非线性理论。
方向四:引力与相对论天体物理。
五、专业课程开设具体要求课程编号:001课程名称:高等量子力学英文名称:Advanced Quantum Mechancs教学内容:第一章:量子态的描述;第二章:量子力学与经典力学的关系;第三章:路径积分;第四章:量子力学中的相位;第五章:二次量子化;第六章:角动量理论;第七章:量子体系的对称性;第八章:时空反演;第九章:散射理论;第十章:相对论量子力学预修课程:大学本科物理专业课程主要教材及参考文献:1、曾谨言.量子力学(卷Ⅱ) [M].2、余寿绵.高等量子力学[M].3、P.Roman, Advanced Quantum Theory[M].4、J.Bjorken etal.Relativistic Quantum Mechanics[M].课程编号:002课程名称:群论英文名称:Group Theory教学内容:第一章:群的基本知识10学时,第二章:群的线性表示10学时;第三章:对称群及其表示10学时;第四章:点群及其表示10学时;第五章:连续群和李代数10学时;第六章:转动群的表示论10学时;第七章:Lorentz群的表示论10学时。