系综理论-课件(PPT·精·选)

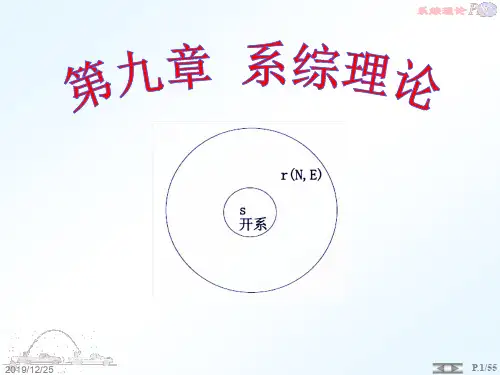
为子相空间。

其中N个点对应相空间的关系可以这样考虑：相空间与相空间。

在某些条件下，发，用整个系统的广义坐标和广义动量所张开的空间来描述系统的状态，这个相空间称为μΓΓμΓμΓ处理粒子间有强相互作用这类问题，不能用分子(相空间，而要用系统(两者都表示一个运动状态，后者是前者的集合。

))相空间。

直接从整个系统状态出相空间的一个点；ΓNr 2Γ空间：以描述系统状态的广义坐标和广义动量为轴构成系统在某一时刻的运动状态，可用称为系统运动状态的代表点。

的笛卡尔坐标空间。

（此空间有个维数）空间中的一点表示，空间。

系统任意时刻的运动状态可以用维的空间就是上述提到的个广义坐标Nr f =二、两种统计平均（1）时间平均（2）系综平均比如在经典力学的范畴内，一个由N个粒子组成的，有相互作用的经典系统的自由度数目，r f f q q L 1f P P L 1f q q L 1f P P L 1f 2ΓΓΓ这样一个经典系统在任意时刻的运动状态可以由该时刻的，以及与之共轭的广义动量来描述。

以，构成的一点来描述，这即是运动状态的代表点。

当系统的运动状态随时间改变时，其代表点就在随时间变化从而划出一条轨道，这个轨道称为系统的相轨道。

为一个粒子的自由度，空间的空间中根据外部条件的不同可以将系综分为三类：（1）微正则系综：孤立系统N、E、V不变（2）正则系综：N、V、T不变，设想与大热源接触μ不变，设想与热源、粒子源接触。

（3）巨正则系综：V、T、之间的一个窄范围内，系统不可能有处在这个能量范围之外的微观状态。

在一宏观条件：孤立系统:N 、E 、V 保持不变（对连续问题，E 在一个能壳范围内）一、微正则分布：ρE E E Δ+E E E Δ+孤立系统的能量具有确定值，更精确地说能量在和和的微观状态数是大量的，而且每一个可能的微观状态出现的概率都相等，这称为等概率原理，即等几原理。

等概率原理：对于平衡态的孤立系统（属于同一能量和相同粒子数），系统的一切微观态出现的概率是相等的。

第九章系综理论第一节刘维尔定理第节相空间第节微正则分布第二节第三节微正则分布的热力学公式第四节正则分布第五节正则分布的热力学公式第九章近独立粒子的最概然分布Boltzmann统计，玻色统计和费米统计。

玻耳兹曼系统：粒子可以分辨，每一个个体量子玻耳兹曼系统粒子可以分辨每个个体量子态能够容纳的粒子数不受限制。

玻色系统：粒子不可分辨，每一个个体量子态能够容纳的粒子数不受限制。

够容纳的粒子数不受限制费米系统：粒子不可分辨，每一个个体量子态最多能够容纳一个粒子。

玻耳兹曼统计是假设系统由大量全同近独立的粒子组成，具有确定的粒子数，能量，体积N E .V 能级：，，，简并度: ，，，1E 2E lE 1ω2ωl ω离子数:，，，1a 2a l a E α=−则在能级上的粒子数为，系数与由与确定。

ll l e a βω=αβN a l =∑E E a l l =∑ll定域系统（由定域粒子组成的系统）与满足经典极限条件的玻色（费米）系统（，或者对于所的1>>αe ,l 1<<l a 又叫做非简并条件）都遵从玻耳兹曼分布。

不满足上述条件的系统遵从玻色统计分布或者费米统计l ω分布。

玻色统计分布满足，费米统计分1−=+l E l l e a βαω布满足。

系数与由与1+=+lE l l e a βαωαβN a ll =∑确定。

E E a l l l=∑9.19.1相空间刘维尔定理目的：说明系综理论的适用范围。

介绍相空间的概念。

给出并且证明刘维尔定理。

内容如下：1系综理论的适用范围是研究相互作用粒子组成的系统1. 系综理论的适用范围是研究相互作用粒子组成的系统。

2. 相空间的概念：设系统在任意时刻的运动状态由个广义坐标和相应的个广义动量在该时刻的数值确定，系统的自由度为。

那末这维空间就是相空间或者叫f q q q ,...,21f fp p p ,...,21f 个变量构成的维空间就是相空间，或者叫空间f f 2f2Γ3.刘维尔定理如下：设有大量结构完全相同的系统，这些系统的运动状态的代表点将在相空间中形成个分布代表点将在相空间中形成一个分布,用表示相空间中的一个体积元。