第二章 第一节 圆曲线半径

第二章圆曲线要素及计算公式
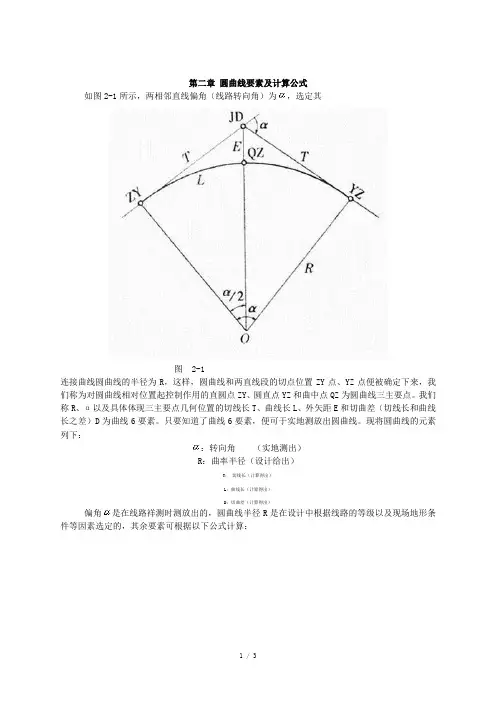
如图2-1所示，两相邻直线偏角（线路转向角）为，选定其
图2-1
连接曲线圆曲线的半径为R，这样，圆曲线和两直线段的切点位置ZY点、YZ点便被确定下来，我们称为对圆曲线相对位置起控制作用的直圆点ZY、圆直点YZ和曲中点QZ为圆曲线三主要点。

我们称R、α以及具体体现三主要点几何位置的切线长T、曲线长L、外矢距E和切曲差（切线长和曲线长之差）D为曲线6要素。

只要知道了曲线6要素，便可于实地测放出圆曲线。

现将圆曲线的元素列下：
：转向角（实地测出）
R：曲率半径（设计给出）
T：切线长（计算得出）
L：曲线长（计算得出）
D：切曲差（计算得出）
偏角是在线路祥测时测放出的，圆曲线半径R是在设计中根据线路的等级以及现场地形条件等因素选定的，其余要素可根据以下公式计算：
温馨提示：最好仔细阅读后才下载使用，万分感谢！。

第十章 曲线测设曲线测设是施工测量中的常用方法，是测量工作的一项重要技术。

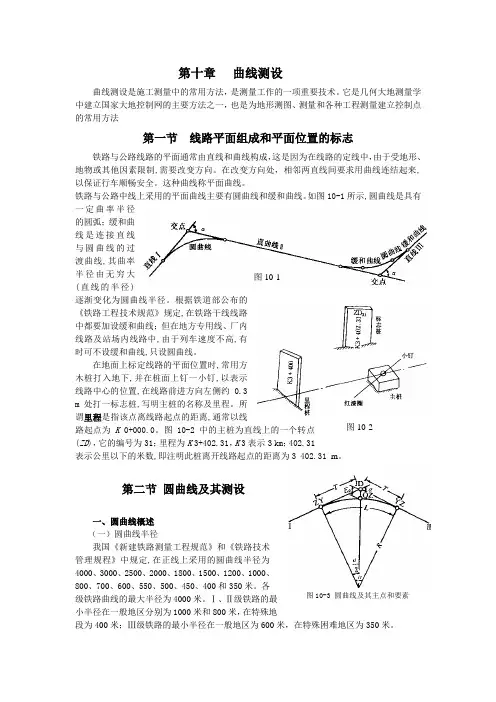
它是几何大地测量学中建立国家大地控制网的主要方法之一，也是为地形测图、测量和各种工程测量建立控制点的常用方法第一节 线路平面组成和平面位置的标志铁路与公路线路的平面通常由直线和曲线构成，这是因为在线路的定线中，由于受地形、地物或其他因素限制,需要改变方向。

在改变方向处，相邻两直线间要求用曲线连结起来,以保证行车顺畅安全。

这种曲线称平面曲线。

铁路与公路中线上采用的平面曲线主要有圆曲线和缓和曲线。

如图10-1所示,圆曲线是具有一定曲率半径的圆弧；缓和曲线是连接直线与圆曲线的过渡曲线,其曲率半径由无穷大(直线的半径)逐渐变化为圆曲线半径。

根据铁道部公布的《铁路工程技术规范》规定,在铁路干线线路中都要加设缓和曲线；但在地方专用线、厂内线路及站场内线路中,由于列车速度不高,有时可不设缓和曲线,只设圆曲线。

在地面上标定线路的平面位置时,常用方木桩打入地下,并在桩面上钉一小钉,以表示线路中心的位置,在线路前进方向左侧约0.3 m 处打一标志桩,写明主桩的名称及里程。

所谓里程是指该点离线路起点的距离,通常以线路起点为K 0+000.0。

图10-2中的主桩为直线上的一个转点(ZD )，它的编号为31；里程为K 3+402.31，K 3表示3 km ；402.31 表示公里以下的米数,即注明此桩离开线路起点的距离为3 402.31 m 。

第二节 圆曲线及其测设一、圆曲线概述 （一）圆曲线半径我国《新建铁路测量工程规范》和《铁路技术管理规程》中规定,在正线上采用的圆曲线半径为4000、3000、2500、2000、1800、1500、1200、1000、800、700、600、550、500、450、400和350米。

各级铁路曲线的最大半径为4000米。

Ⅰ、Ⅱ级铁路的最小半径在一般地区分别为1000米和800米，在特殊地段为400米；Ⅲ级铁路的最小半径在一般地区为600米，在特殊困难地区为350米。

2021-2022年高中数学第二章综合曲线与方程知识精讲文北师大版选修1－1一、教学内容选修1－1 曲线与方程二、教学目标1、理解曲线与方程的概念及进一步认识坐标法的应用。

2、能用直译法、定义法、相关点法等方法求简单的曲线方程。

3、进一步培养学生对数学思想方法的应用能力、推理能力、计算能力。

三、知识要点分析1、曲线的方程与方程的曲线在平面直角坐标系中，曲线C上的点与二元方程f（x，y）=0的实数解建立如下关系：（1）曲线上的点的坐标x，y都是方程f（x，y）=0的解。

（2）以方程f（x，y）=0的解x，y为坐标的点（x，y）都在曲线C上。

则曲线C叫方程f（x，y）=0的曲线，方程f（x，y）=0叫曲线C的方程。

2、求曲线方程的步骤：（1）建系——建立适当的坐标系。

（2）设点——设轨迹上任意点P（x，y）（3）列式——写出满足某种条件的动点P（x，y）的关系式。

（4）代换——将动点P（x，y）转化为f（x，y）=0并化简。

（5）证明——证明所求的方程为符合条件的动点轨迹方程。

3、求曲线轨迹方程的几种常用的方法：求曲线的轨迹方程常采用的方法有直译法、定义法、代入法、参数法。

（1）直译法：是将动点满足的几何条件或者等量关系，直接坐标化，列出等式化简即得动点轨迹方程。

（2）定义法：若动点轨迹的条件符合某一基本轨迹的定义（如椭圆、双曲线、抛物线、圆等），可用定义直接探求。

（3）相关点法：根据相关点所满足的方程，通过转换而求动点的轨迹方程。

【典型例题】考点一：用直译法求曲线的轨迹方程例1：已知A、B为两定点，动点M到A与到B的距离比为正的常数λ，求点M的轨迹方程。

【思路分析】可设|AB|=2a（a>0），然后建立如图所示的坐标系，此时A（－a，0），B （a，0），设M的坐标为（x，y），表示出|MA|，|MB|，根据已知条件得：，然后再化简。

解：建立坐标系如图所示，设M （x ，y ）是轨迹上任意一点。

圆曲线要素及计算公式前言《礼记》有云：大学之道，在明德，在亲民。

在提笔撰写我的毕业设计论文的时候，我也在向我的大学生活做最后的告别仪式。

我不清楚过去的一切留给现在的我一些什么，也无从知晓未来将赋予我什么，但只要流泪流汗，拼过闯过，人生才会少些遗憾！非常幸运能够加入水利工程这个古老而又新兴的行业，即将走向工作岗位的时刻，我仿佛感受到水利行业对我赋予新的历史使命，水利是一项以除害兴利、趋利避害，协调人与水、人与大自然关系的高尚事业。

水利工作，既要防止水对人的侵害，更要防止人对水的侵害；既要化解自然灾害对人类生命财产的威胁，又要善待自然、善待江河、善待水，促进人水和谐，实现人与自然和谐相处。

这种使命，更让我用课堂中的知识用于实际生产中来。

特别是这两个月来的毕业设计，我越发感觉到学会学精测量基础知识对于我贡献水利是多么的重要。

所以，我越发不愿放弃不多的大学时光，努力提高自己的实践动手能力，而本学期的毕业设计，为我提供了绝好的机会，我又怎能放弃？刚刚从老师那里得到毕业设计的题目和任务时，我的心里真的没底。

作为毕业设计的主体工作，我们主要运用电子水准仪对某幢建筑物进行变形观测与计算，布设控制点进行平面控制测量和高程控制测量；用全站仪进行了中心多边行角度和距离的测量，并用条件平差原理进行平差，通过控制点的放样来计算土的挖方量，还有圆曲线的计算与测设。

而我研究的毕业课题是圆曲线测设。

大学的最后一个学期过得特别快，几乎每天扛着仪器，奔走在校园的每个角落，生活亦很有节奏。

今天我提笔写毕业论文，我的毕业设计也接近尾声。

不管成果如何，毕竟心里不再是没底了，挑着两个多月的辛苦换来的数据和成果，并不断的完善他们，心里感觉踏实多了。

在本次毕业设计论文的设计中要感谢水利系为我们的工作提供了测量仪器，还有各指导老师的教导和同学的帮助。

摘要：在公路、铁路的路线圆曲线测设中，一般是在测设出曲线各主点后，随之在直圆点或圆直点进行圆曲线详细测设。

简述圆曲线半径的类型及适用条件在数学和物理学中，圆曲线是一种常见的曲线形式。

圆曲线半径的类型和适用条件是圆曲线研究的重要内容。

本文将对圆曲线半径的类型和适用条件进行简述。

下面是本店铺为大家精心编写的3篇《简述圆曲线半径的类型及适用条件》，供大家借鉴与参考，希望对大家有所帮助。

《简述圆曲线半径的类型及适用条件》篇1一、圆曲线半径的类型圆曲线半径是指圆曲线上某一点的曲率半径。

根据圆曲线的曲率性质，圆曲线半径可以分为以下几种类型:1. 常数半径圆曲线：其半径为一个常数，即在圆曲线上所有点的曲率半径都相等。

2. 变量半径圆曲线：其半径为一个变量，即在圆曲线上不同点的曲率半径不同。

3. 径向变量半径圆曲线：其半径是一个径向变量，即在圆曲线上不同点的曲率半径与该点到圆心的距离有关。

4. 切向变量半径圆曲线：其半径是一个切向变量，即在圆曲线上不同点的曲率半径与该点处的切线方向有关。

二、圆曲线半径的适用条件圆曲线半径的适用条件主要取决于圆曲线的曲线形式和应用场景。

以下是一些常见的适用条件:1. 常数半径圆曲线适用于圆形、椭圆形等曲线，其半径为一个常数，适用于各种曲线形式。

2. 变量半径圆曲线适用于一些复杂的曲线形式，如螺旋线、花瓣曲线等，其半径随着曲线的变化而变化。

3. 径向变量半径圆曲线适用于一些具有径向对称性的曲线形式，如行星轨道、太阳系天体运动等，其半径随着距离圆心的距离的变化而变化。

4. 切向变量半径圆曲线适用于一些具有切向对称性的曲线形式，如涡旋、龙卷风等，其半径随着切线方向的变化而变化。

圆曲线半径的类型和适用条件是圆曲线研究的重要内容。

《简述圆曲线半径的类型及适用条件》篇2圆曲线半径是一种用于描述圆曲线的参数，它通常用于计算机图形学、数学和物理学等领域。

圆曲线半径有多种类型，每种类型都有其适用条件。

1. 常数半径：常数半径是指在圆曲线上，所有点的半径都相等的情况。

常数半径适用于圆曲线上的点是等距离分布的情况，例如圆形、正多边形等。

注：括号值为路拱大于2%时的不设超高最小半径
新的路线设计规范要求超高应该按照运行速度进行选取。

在进行运行速度计算后，根据这个公式反算
R=V2/127（f+i）
式中：V—运行速度(km/h)；
f—路面与轮胎间的横向力系数；
i—路面超高横坡度。

超高过渡段长度按下式计算：
LC = B △i/P
式中：LC —超高过渡段长度(m)；
B —旋转轴至行车道(设路缘带时为路缘带)外侧边缘的宽度(m)；
△i—超高坡度与路拱坡度的代数差(%)；
P —超高渐变率，即旋转轴与行车道(设路缘带时为路缘带) 外侧边缘线之间的相对坡度，其值如表7.5.4。

根据上式求得过渡段长度，应凑整成5m的倍数，并不小于20m的长度。

圆曲线半径
圆曲线半径是数学中最重要的概念之一，它有着深远的意义，影响着许多方面的计算和问题的解决。

为了更有效地利用圆曲线半径，本文将详细阐述它的定义、特性、计算方法以及一些实际应用。

从数学的角度来看，圆曲线半径定义为圆曲线中总长度与上下限（即有限范围）之比。

这意味着，当我们在一个有限的范围内，给定一条圆曲线，我们可以通过以下计算，求出这条圆曲线的圆曲线半径：首先，求出圆曲线上下限之间的总长度，然后将其除以上下限之比，得到的即是此圆曲线的半径。

圆曲线半径具有多种特征，其中最重要的是它可以指示出圆曲线的大小和形状。

换句话说，圆曲线半径可以用来衡量圆曲线的复杂度，例如，若一条圆曲线具有较大的圆曲线半径，则表明此圆曲线更加复杂，反之则简单。

此外，圆曲线半径也可用来比较圆曲线的长度，从而提供有效的圆曲线相似性检测的基础。

此外，圆曲线半径还可以用于计算问题及其答案的解决方案。

例如，如果要解决一个复杂的数学问题，我们可以通过寻找具有较大半径的圆曲线，从而求出问题的解决方案。

此外，圆曲线半径还可用于计算任意轨迹的圆心，而这些轨迹的圆心也可以用于求解更加复杂的问题。

此外，圆曲线半径还有广泛的实际应用，例如在机器视觉领域，它可以用于检测和识别图像特征；在机械设计领域，它可用于求解机械零件的外形形状；在视频服务器端，它可以用于提高视频流质量，
以便更好地进行视频流媒体服务。

综上所述，圆曲线半径是一个重要的数学概念，它在数学领域有着重要的意义，同时也有许多实际应用。

通过本文的介绍，可以更有效地利用圆曲线半径，从而实现一系列理想的结果。