圆曲线半径
- 格式:pptx
- 大小:466.57 KB
- 文档页数:4

圆曲线切线长公式
在几何学中,圆曲线的切线长是曲线在某一点的切线长度。
在道路设计和施工等许多领域,圆曲线切线长是一个重要的参数。
本文将介绍圆曲线切线长的计算公式。
首先,我们需要知道圆曲线的半径R和圆心角θ。
圆心角通常用弧度表示,它描述了曲线偏离直线的程度。
圆曲线切线长的计算公式为:T=R×θ
其中T为圆曲线切线长,R为圆曲线半径,θ为圆心角(弧度)。
这个公式简单明了,易于理解和应用。
为了更好地理解这个公式,我们可以看一个具体的例子。
假设一条道路转弯处的圆曲线半径为30米,圆心角为60度(弧度),那么圆曲线切线长就是:T=30×(60/180)π=10π≈31.4米
这个结果告诉我们,在这个转弯处,道路的直线部分应该至少有31.4米的长度,才能平滑地过渡到圆曲线上。
在实际应用中,圆曲线切线长的计算还需要考虑其他因素,如道路宽度、车辆速度、交通流量等。
因此,在设计道路时,我们需要根据实际情况对圆曲线切线长进行精细化计算,以确保道路的安全性和舒适性。
总之,圆曲线切线长的计算公式是T=R×θ,其中T为圆曲线切线长,R为圆曲线半径,θ为圆心角(弧度)。
这个公式简单实用,是道路设计中的重要工具。

一、概述圆曲线是道路、铁路等工程中常见的曲线形式,其设计和计算对工程建设具有重要意义。
在圆曲线中,曲线元素的计算是一项关键工作,而主点里程公式则是计算圆曲线主点里程的重要方法之一。
本文将对圆曲线元素计算和主点里程公式进行介绍和分析。
二、圆曲线元素计算圆曲线的设计和建设需要对其曲率、切线角等曲线元素进行精确的计算。
曲线元素的计算是通过复杂的数学方法和公式进行的,主要包括以下几个步骤:1. 曲率半径的计算圆曲线的曲率半径是曲线的一个重要参数,它反映了曲线的弯曲程度。
曲率半径的计算是通过测量曲线的实际弧长以及曲线的夹角来完成的,具体的计算方法是利用三角函数公式来求解。
2. 切线角的计算在圆曲线的设计中,切线角是一个重要的参量,它可以影响车辆或列车在曲线上行驶时的安全性和稳定性。
切线角的计算是通过测量曲线的实际弧长和曲线的曲率半径来完成的,具体的计算方法同样是利用三角函数公式来求解。
3. 圆曲线上任意点的坐标计算在实际的工程设计中,常常需要知道圆曲线上任意点的坐标,以便进行进一步的设计和施工。
圆曲线上任意点的坐标计算是通过数学方法和几何原理进行的,其中涉及到参数方程、极坐标等数学概念和公式。
三、主点里程公式主点里程是指在道路或铁路设计中,与特定主要参考点(如桥梁、隧道等)相对应的里程值。
在圆曲线设计中,计算主点里程是确保设计和施工准确性的重要步骤。
主点里程的计算可以通过主点里程公式来完成,其具体表达式如下:主点里程 = 基准点里程 + 曲线长度 * (1 + (曲线长度 / 2 * 曲线半径)) / 2在这个公式中,基准点里程是从起始点到基准点的里程值,曲线长度是圆弧的长度,曲线半径是圆曲线的曲率半径。
四、总结圆曲线元素计算和主点里程公式是圆曲线设计中两个重要的计算方法。
通过精确的曲线元素计算和主点里程计算,可以确保圆曲线设计的精准性和可靠性。
在实际工程中,工程师和设计人员需要注意这些计算方法的细节和技巧,以保证工程建设的高质量和安全性。

一级公路最小圆曲线半径稿子一:嗨,朋友们!今天咱们来聊聊一级公路最小圆曲线半径这个话题。
你们知道吗,这最小圆曲线半径啊,就像是公路的小脾气,可得好好琢磨。
它可不是随便定的,那是有讲究的!想象一下,要是这半径太小了,司机开车在上面拐来拐去,多吓人呀!就像坐过山车一样,心里直突突。
而且车也容易失控,多危险呐!那为啥要有个最小的限制呢?这就好比咱们跑步,弯道太急,是不是容易摔跟头?公路也一样,半径太小,车辆转弯的难度就大,速度不好控制,事故就容易找上门。
所以啊,设计师们在规划一级公路的时候,得把这个最小圆曲线半径考虑得妥妥的。
要让司机们开得顺顺当当,安安全全的。
再说啦,这半径大小还和地形有关系呢。
要是在山区,路本来就不好修,那半径可能就得稍微大一些,不然车在山上转来转去,司机的小心脏可受不了。
呢,一级公路最小圆曲线半径可不是个小事情,关系着咱们的出行安全和舒适。
大家以后在路上开车,也可以留意留意这些弯弯绕绕,感受一下公路设计的巧妙之处哟!稿子二:亲爱的小伙伴们,今天咱们来扯扯一级公路最小圆曲线半径!哎呀,一说这个,是不是感觉有点专业?别担心,听我慢慢道来。
其实啊,这就好比咱们玩的赛车游戏,赛道上的弯道大小可重要啦!一级公路也一样,圆曲线半径不能太小。
要是太小了,车子拐起来费劲不说,还容易跑偏。
你想啊,一辆大货车呼呼地开着,突然遇到个小半径的弯道,那不得吓出一身冷汗!而且哦,这半径还影响着咱们坐车的感受。
太小的话,左摇右晃,能把人给晃晕喽!设计师们在定这个最小半径的时候,那可是费了不少心思。
要考虑车流量、车速,还得看看周围的环境。
比如说,在平坦的地方,半径可以稍微小一点,但也不能太过分。
要是在河边或者悬崖边,那可得大大地放大半径,保证安全第一。
另外呀,不同的车型对这个半径的要求也不一样。
小汽车灵活点,能适应稍微小一点的半径,可大货车、大客车就不行啦,得给它们留出足够的空间。
呢,一级公路最小圆曲线半径可关系着咱们的出行,大家多了解了解,以后在路上也能更明白为啥路是这样修的啦!。

缓和曲线、竖曲线、圆曲线、匝道(计算公式)一、缓和曲线上的点坐标计算已知:①缓和曲线上任一点离ZH点的长度:l②圆曲线的半径:R③缓和曲线的长度:l0④转向角系数:K(1或-1)⑤过ZH点的切线方位角:α⑥点ZH的坐标:xZ,yZ计算过程:说明:当曲线为左转向时,K=1,为右转向时,K=-1,公式中n的取值如下:当计算第二缓和曲线上的点坐标时,则:l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与计算第一缓和曲线时相反xZ,yZ为点HZ的坐标切线角计算公式:二、圆曲线上的点坐标计算已知:①圆曲线上任一点离ZH点的长度:l②圆曲线的半径:R③缓和曲线的长度:l0④转向角系数:K(1或-1)⑤过ZH点的切线方位角:α⑥点ZH的坐标:xZ,yZ计算过程:说明:当曲线为左转向时,K=1,为右转向时,K=-1,公式中n的取值如下:当只知道HZ点的坐标时,则:l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与知道ZH点坐标时相反xZ,yZ为点HZ的坐标三、曲线要素计算公式公式中各符号说明:l——任意点到起点的曲线长度(或缓曲上任意点到缓曲起点的长度)l1——第一缓和曲线长度l2——第二缓和曲线长度l0——对应的缓和曲线长度R——圆曲线半径R1——曲线起点处的半径R2——曲线终点处的半径P1——曲线起点处的曲率P2——曲线终点处的曲率α——曲线转角值四、竖曲线上高程计算已知:①第一坡度:i1(上坡为“+”,下坡为“-”)②第二坡度:i2(上坡为“+”,下坡为“-”)③变坡点桩号:SZ④变坡点高程:HZ⑤竖曲线的切线长度:T⑥待求点桩号:S计算过程:五、超高缓和过渡段的横坡计算已知:如图,第一横坡:i1第二横坡:i2过渡段长度:L待求处离第二横坡点(过渡段终点)的距离:x 求:待求处的横坡:i解:d=x/Li=(i2-i1)(1-3d2+2d3)+i1六、匝道坐标计算已知:①待求点桩号:K②曲线起点桩号:K0③曲线终点桩号:K1④曲线起点坐标:x0,y0⑤曲线起点切线方位角:α0⑥曲线起点处曲率:P0(左转为“-”,右转为“+”)⑦曲线终点处曲率:P1(左转为“-”,右转为“+”) 求:①线路匝道上点的坐标:xy②待求点的切线方位角:αT计算过程:注:sgn(x)函数是取符号函数,当x0。


圆曲线(偏角法,切线支距法,极坐标法一、圆曲线测量方法(一)偏角法1. 原理- 偏角法是以曲线起点(或终点)至曲线上任一点的弦线与切线之间的弦切角(偏角)和弦长来确定待放点的位置。
- 设圆曲线半径为R,弧长为l,对应的圆心角为φ(弧度制),则φ=(l)/(R)。
偏角δ=(φ)/(2)(因为弦切角等于圆心角的一半)。
2. 计算步骤- 首先计算圆曲线的要素,如切线长T = Rtan(α)/(2)(α为圆曲线的转角),曲线长L = Rα(α为弧度制),外矢距E = R(sec(α)/(2)-1)。
- 然后将曲线按一定的弧长l进行分段(一般为等分段),计算每段弧长对应的偏角δ_i。
- 对于第i段弧长l_i,偏角δ_i=(l_i)/(2R)(弧度制),换算为度分秒形式方便测量。
- 根据起点(或终点)的切线方向,依次拨出偏角δ_i,并量取相应的弦长c_i = 2Rsinδ_i,从而确定曲线上各点的位置。
(二)切线支距法1. 原理- 切线支距法是以曲线起点(或终点)为坐标原点,以切线为x轴,过原点的半径为y轴,建立直角坐标系。
曲线上任一点P的位置用坐标(x,y)表示,根据圆曲线的方程来计算坐标值。
- 圆曲线的方程为y = R(1 - cosφ),x = Rsinφ,其中φ为圆心角(从起点到该点所对应的圆心角)。
2. 计算步骤- 同样先计算圆曲线的要素。
- 将曲线按一定的圆心角Δφ进行分段(一般为等分段)。
- 对于第i段圆心角φ_i = iΔφ,计算该点的坐标x_i = Rsinφ_i,y_i = R(1 - cosφ_i)。
- 根据计算出的坐标值,从原点沿切线方向量取x值,再垂直于切线方向量取y 值,从而确定曲线上各点的位置。
(三)极坐标法1. 原理- 极坐标法是在已知控制点的基础上,以控制点为极点,以某一方向为极轴,通过测量待定点相对于极点的极径ρ和极角θ来确定待定点的位置。
- 在圆曲线测量中,一般以曲线起点(或终点)附近的控制点为极点,以切线方向为极轴方向。

速公路的一些线路坐标、高程计算公式(缓和曲线、竖曲线、圆曲线、匝道) 一、缓和曲线上的点坐标计算已知:①缓和曲线上任一点离ZH点的长度:l②圆曲线的半径:R③缓和曲线的长度:l④转向角系数:K(1或-1)⑤过ZH点的切线方位角:α⑥点ZH的坐标:xZ ,yZ计算过程:说明:当曲线为左转向时,K=1,为右转向时,K=-1,公式中n的取值如下:当计算第二缓和曲线上的点坐标时,则:l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与计算第一缓和曲线时相反x Z ,yZ为点HZ的坐标切线角计算公式:二、圆曲线上的点坐标计算已知:①圆曲线上任一点离ZH点的长度:l②圆曲线的半径:R③缓和曲线的长度:l④转向角系数:K(1或-1)⑤过ZH点的切线方位角:α⑥点ZH的坐标:xZ ,yZ计算过程:说明:当曲线为左转向时,K=1,为右转向时,K=-1,公式中n的取值如下:当只知道HZ点的坐标时,则:l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与知道ZH点坐标时相反x Z ,yZ为点HZ的坐标三、曲线要素计算公式公式中各符号说明:l——任意点到起点的曲线长度(或缓曲上任意点到缓曲起点的长度)l1——第一缓和曲线长度l2——第二缓和曲线长度l——对应的缓和曲线长度R——圆曲线半径R1——曲线起点处的半径R 2——曲线终点处的半径P——曲线起点处的曲率1——曲线终点处的曲率P2α——曲线转角值四、竖曲线上高程计算已知:①第一坡度:i(上坡为“+”,下坡为“-”)1(上坡为“+”,下坡为“-”)②第二坡度:i2③变坡点桩号:SZ④变坡点高程:HZ⑤竖曲线的切线长度:T⑥待求点桩号:S计算过程:五、超高缓和过渡段的横坡计算已知:如图,第一横坡:i1第二横坡:i2过渡段长度:L待求处离第二横坡点(过渡段终点)的距离:x 求:待求处的横坡:i解:d=x/Li=(i2-i1)(1-3d2+2d3)+i1六、匝道坐标计算已知:①待求点桩号:K②曲线起点桩号:K③曲线终点桩号:K1④曲线起点坐标:x0,y⑤曲线起点切线方位角:α⑥曲线起点处曲率:P(左转为“-”,右转为“+”)⑦曲线终点处曲率:P(左转为“-”,右转为“+”)1求:①线路匝道上点的坐标:x,y②待求点的切线方位角:αT计算过程:注:sgn(x)函数是取符号函数,当x<0时sgn(x)=-1,当x>0时sgn(x)=1,当x=0时sgn(x)=0。

一、圆曲线范围公式
已知:半径R.转向角β
1、切线长T=Rtan(β/2)
2、曲线长L=(Rπβ)/180
3、外矢距E=R(1/cos(β/2)-1)
4、切曲差q=2T-L
偏角公式δ=180C/2Rπ注C为所点弧长
二、缓和曲线范围公式
1、缓和曲线切线角βn=90Ln2/RπLs Ln为所点n到直缓或缓直点曲线长Ls---缓和曲线长
2、缓和曲线偏角公式:
δn=30 Ln2/RπLs
3、切线长T=m+(R+P)tan(β/2)
4、曲线长:
L=(Rπ(β-2β0))/180+2Ls
5、外矢距E=(R+P)/cos(β/2)-R
6、切曲差q=2T-L
7、切垂距m=Ls/2-Ls3/240R2
8、内移距P=Ls2/24R- Ls4/2688R3
9、缓和曲线数学坐标公式:
X=Ls-Ln5/40R2Ls2
Y= Ln3/6RLs- Ln7/336 R3Ls3
10、缓和曲线偏角公式:
δn=tan-1(y/x)
11、缓和曲线弦长公式:Ci=√(x2+y2) Cc=Ln-Ln3/90R2+Ln5/3888 R4(代数式综合曲线中圆曲线范围坐标公式:Xi=m+Li-Ls/2-(Li-Ls/2)3/6R2
Yi=p+(Li- Ls/2)2/2R-(Li- Ls/2)4/24R3注:Li为圆曲线上任意点到ZH或
HZ的曲线长(用于计算偏移值)三、竖曲线计算公式
Y=X2/2R。

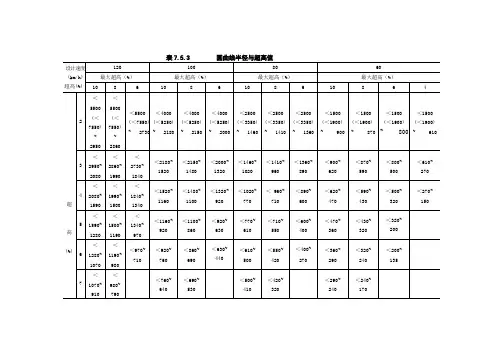
注:括号值为路拱大于2%时的不设超高最小半径
新的路线设计规范要求超高应该按照运行速度进行选取。
在进行运行速度计算后,根据这个公式反算
R=V2/127(f+i)
式中:V—运行速度(km/h);
f—路面与轮胎间的横向力系数;
i—路面超高横坡度。
超高过渡段长度按下式计算:
LC = B △i/P
式中: LC —超高过渡段长度(m);
B —旋转轴至行车道(设路缘带时为路缘带)外侧边缘的宽度(m);
△i—超高坡度与路拱坡度的代数差(%);
P —超高渐变率,即旋转轴与行车道(设路缘带时为路缘带) 外侧边缘线之间的相对坡度,其值如表7.5.4。
根据上式求得过渡段长度,应凑整成5m的倍数,并不小于20m的长度。
(注:本资料素材和资料部分来自网络,仅供参考。
请预览后才下载,期待您的好评与关注!)。
注:括号值为路拱大于2%时的不设超高最小半径新的路线设计规范要求超高应该按照运行速度进行选取。
在进行运行速度计算后,根据这个公式反算
R=V2/127(f+i)
式中:V—运行速度(km/h);
f—路面与轮胎间的横向力系数;
i—路面超高横坡度。
超高过渡段长度按下式计算:
LC = B △i/P
式中:LC —超高过渡段长度(m);
B —旋转轴至行车道(设路缘带时为路缘带)外侧边缘的宽度(m);
△i—超高坡度与路拱坡度的代数差(%);
P —超高渐变率,即旋转轴与行车道(设路缘带时为路缘带) 外侧边缘线之间的相对坡度,其值如表7.5.4。
根据上式求得过渡段长度,应凑整成5m的倍数,并不小于20m的长度。
第二章圆曲线要素及计算公式
如图2-1所示,两相邻直线偏角(线路转向角)为,选定其
图 2-1
连接曲线圆曲线的半径为R,这样,圆曲线和两直线段的切点位置ZY点、YZ点便被确定下来,我们称为对圆曲线相对位置起控制作用的直圆点ZY、圆直点YZ和曲中点QZ为圆曲线三主要点。
我们称R、α以及具体体现三主要点几何位置的切线长T、曲线长L、外矢距E和切曲差(切线长和曲线长之差)D为曲线6要素。
只要知道了曲线6要素,便可于实地测放出圆曲线。
现将圆曲线的元素列下:
:转向角(实地测出)
R:曲率半径(设计给出)
T:切线长(计算得出)
L:曲线长(计算得出)
D:切曲差(计算得出)
偏角是在线路祥测时测放出的,圆曲线半径R是在设计中根据线路的等级以及现场
地形条件等因素选定的,其余要素可根据以下公式计算:。
横净距圆曲线半径概述说明以及解释1. 引言1.1 概述在道路设计与规划中,横净距和圆曲线半径是两个重要的概念。
横净距指的是道路两侧各种设施或障碍物(如护栏、建筑物、广告牌等)离车行道边缘的水平距离。
而圆曲线半径则是指圆弧形状道路中心线所组成的圆,该圆的半径即为圆曲线半径。
1.2 文章结构本文将首先对横净距和圆曲线半径进行定义和解释,明确其含义和作用。
接着探讨横净距和圆曲线半径分别受到哪些因素的影响,以便更好地理解其设计原则和应用。
针对这些因素,我们还将介绍相应的设计与验算方法。
然后,在文章的最后一部分中,我们将对整个内容进行概述说明,总结横净距和圆曲线半径之间的关系,并提出相关设计原则与指导要点,同时通过实际案例分析和经验总结验证这些原则及应用。
最后,在结论部分,我们将对本文主要观点进行总结,对未来发展进行展望,并提出研究局限及后续研究方向的建议。
1.3 目的本文的目的在于全面阐述横净距和圆曲线半径这两个道路设计中关键要素的概念、作用以及相关设计与计算方法,为道路规划与设计人员提供明确的指导和参考依据。
同时,通过案例分析和经验总结,本文旨在揭示实际应用中可能遇到的问题,并提供解决方案。
2. 横净距2.1 定义与解释横净距是指在道路设计中,两个行车方向相邻的车道之间的垂直距离。
通常情况下,横净距是通过将两个相邻车道之间的中心线竖直延长来测量得到的。
2.2 影响因素横净距的大小受多种因素影响。
主要的影响因素包括以下几点:- 道路类型:不同类型的道路对横净距有着不同的要求。
例如,城市快速道路和高速公路通常需要较大的横净距,以提供更安全和顺畅的交通环境。
- 车辆尺寸:不同类型和尺寸的车辆对横净距有着不同的需求。
大型卡车需要更宽敞的空间来转弯,因此需要更大的横净距。
- 车流量:高流量道路需要更宽阔的横净距以容纳更多车辆并保证交通安全。
- 道路曲率:曲线半径小于一定数值时,会对横净距产生限制。
较小的曲率半径会限制车辆在弯道上的行驶速度和转弯半径。
公路最大圆曲线半径
公路的最大圆曲线半径取决于许多因素,包括设计标准、道路类型、车辆行驶速度和地形条件等。
一般来说,公路的最大圆曲线半径会根据以下几个方面进行确定:
1. 设计标准:每个国家或地区都有自己的道路设计标准,这些标准包括了曲线半径的最小要求,以确保行车安全。
这些标准会基于车辆的行驶速度和设计车型等因素来确定最大圆曲线半径。
2. 道路类型:不同类型的道路(如高速公路、城市道路、乡村道路等)对于曲线半径的要求也不同。
高速公路往往会有较大的曲线半径,以确保车辆在高速行驶时的稳定性和安全性。
3. 车辆行驶速度:车辆的行驶速度也是确定曲线半径的重要因素之一。
行驶速度越高,需要更大的曲线半径来确保车辆的稳定。
4. 地形条件:道路所处的地形条件也会影响曲线半径的大小。
在山区或坡地上,由于地形的限制,曲线半径可能相对较小。
因此,公路的最大圆曲线半径是一个复杂的问题,取决于多个因素的综合考虑。
具体数值会根据实际情况而有所不同。
横净距圆曲线半径全文共四篇示例,供读者参考第一篇示例:横净距是指圆曲线外侧路肩边缘到曲线中心线的水平距离,也就是曲线外侧的路肩到曲线内侧的线段长度。
圆曲线半径则是指圆曲线的半径,是偏曲路段中的一个重要参数。
在道路设计中,两者都是非常重要的指标,对道路的安全性、舒适性和运行效率都有着重要的影响。
横净距和圆曲线半径的设定需要考虑到多方面的因素,包括道路的等级、交通量、车速、曲线情况等等。
在一般道路设计中,横净距通常会根据车辆类型和速度等因素进行设定,以确保车辆在过曲线时有足够的空间进行横向移动,同时还需要考虑到安全性和舒适性的要求。
而圆曲线半径则会受到交通流量、车速、曲线长度等因素的影响,需要根据实际情况进行合理的选择。
在道路设计中,横净距和圆曲线半径的设定是非常重要的,对道路的安全性和舒适性有着直接的影响。
如果横净距设置不当,可能会导致车辆过曲线时存在碰撞风险或者舒适性不佳;而圆曲线半径太小,则可能会导致车辆在过曲线时需要减速过慢,影响交通效率。
在道路设计中,需要充分考虑到这些因素,合理设置横净距和圆曲线半径,以确保道路的安全性和舒适性。
横净距和圆曲线半径的设计也需要考虑到未来交通需求的变化。
随着城市化进程的加快,交通需求也在不断增加,道路的设计需要预留一定的发展空间。
在设定横净距和圆曲线半径时,需要考虑到未来的交通量和车速可能的变化,以确保道路在未来仍然具有良好的运行效率和安全性。
在道路改建和升级中,也需要对现有的道路横净距和圆曲线半径进行评估和优化。
有时候,由于交通流量的增加或者车速的提高,现有的横净距和圆曲线半径可能已经无法满足当前的交通需求,需要对其进行调整。
在进行道路改建和升级时,需要充分考虑到横净距和圆曲线半径的优化,以确保道路在未来仍然能够满足交通需求。
第二篇示例:横净距和圆曲线半径是道路设计中重要的概念,它们直接影响着道路的舒适性、安全性和实用性。
在道路建设计划中,根据交通流量、车速等因素,需要对横净距和圆曲线半径进行合理的设计,以确保车辆在道路上行驶时平稳、安全,并减少交通事故的发生。