圆曲线超高率取值计算

圆曲线超高率取值计算摘要：论述了超高率和摩擦系数的分配方法，分析了各种分配方法的优缺点。

提出了超高率取值设计的计算方法并探讨了纵坡对超高的影响，提出了超高率的取值应根据公路纵坡进行调整。

关键词：公路工程超高率摩擦系数纵坡影响1概述近年来，随着我国的公路建设的迅猛发展，灵活性设计理念已深入人心，超高计算取值则是其中的一个重要体现。

本文在超高率和摩擦系数抵消车辆在曲线路段上行驶时所产生的离心力的分配原则为基础，对公路圆曲线上超高率的取值进行了定量与定性相结合的分析。

2超高率和横向摩擦系数在曲线范围内的分配2.1分配的方法对某一既定的设计速度，可采用超高或横向摩擦系数或同时采用两者，以平衡车辆行驶在曲线上时所受的离心力，具体有以下五种方法[1]如图1所示。

方法①：超高e和横向摩擦系数f与平曲线曲率成正比（即在1/R=0和1/R=1/Rmax之间的直线关系）。

方法②：以设计速度行驶的汽车在未达到fmax的曲线上时，其离心力完全由横向摩擦力平衡。

当曲线曲率增大时，待摩擦力达到fmax并保持不变，剩余的离心力则由超高来平衡，直至e达到emax。

方法③：以设计速度行驶的汽车在未达到emax的曲线上，其离心力完全由曲线的超高来平衡。

当曲率再大时，超高达到emax并保持不变，这时剩余的离心力是由正比于曲率的横向摩擦力来平衡，直至f达到fmax。

方法④：以运行速度代替设计速度，其余与方法③相同。

方法⑤：认为超高率和横向摩擦系数与曲率成曲线关系，它们的值是介于方法①和方法③所得到的值。

2.2各方法分析比较方法①得出的超高率与曲率的直线关系，计算简单，具有相当的价值而又合乎逻辑。

但该分配方法要求车流中的每辆汽车都是以均速状态行驶，虽然大多数驾驶员都希望以均速行驶，但是只有在交通量不大，设计得很好的公路上才能实现均速行驶，而实际的道路状况往往不是这样，在实际中采用的超高率往往比此方法确定的e值要大，另外使用这种方法，在相当一部分曲线范围内是不用设置最大超高的。

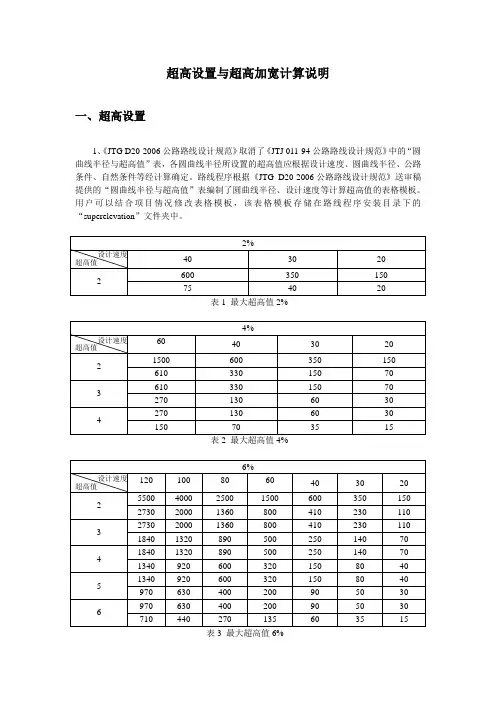
超高设置与超高加宽计算说明一、超高设置1、《JTG D20-2006公路路线设计规范》取消了《JTJ 011-94公路路线设计规范》中的“圆曲线半径与超高值”表，各圆曲线半径所设置的超高值应根据设计速度、圆曲线半径、公路条件、自然条件等经计算确定。

路线程序根据《JTG D20-2006公路路线设计规范》送审稿提供的“圆曲线半径与超高值”表编制了圆曲线半径、设计速度等计算超高值的表格模板。

用户可以结合项目情况修改表格模板，该表格模板存储在路线程序安装目录下的“superelevation”文件夹中。

表5 最大超高值10%2、在超高自动计算前，用户可以先进行超高设置，程序中的命令：[数据处理]→[超高分段] →[超高值设置]，设置窗体如图1图1 超高值设置3、路线程序根据最大超高值自动选用相应的表，若用户需要修改表格模板可点击“浏览”按钮弹出表格模板，然后修改表格模板。

点击“确定”按钮后，程序就会把用户设置的超高值存入数据库，超高自计算就会以用户设置的超高值进行计算。

若用户不进行超高设置，程序会按程序内默认的超高值进行计算。

4、表格模板格式不能修改，只能修改模板中的数据。

二、超高计算命令：[数据处理]→[超高分段] →[自动计算]图2 超高自动计算1、超高自动计算窗体说明(如图2)1、1 当选中窗体中的“全缓和曲线范围内超高”，程序不考虑渐变率计算的超高缓和长度，默认超高在缓和曲线上完成；反之考虑渐变率计算的超高缓和长度。

1、2 当选中窗体中的“S型曲线YH(HY)全超高”，程序认为S型曲线YH（HY）刚好达到全超高，然后向GQ点推；反之由GQ点向YH（HY）推。

1．3 当选中窗体中的“S型曲线公切点横坡0%”，则公切点超高为0%，若未选中，则公切点为正常路拱。

2、超高自动计算时，线元划分成如下单元进行计算：2、1直线——圆曲线和圆曲线——直线（1）中间没有缓和曲线，超高缓和长度直线和圆曲线上各一半。

渐向双坡阶段终点B过渡过程中的一点）。
根据超高渐变规律：AC/AB=X/ L 1
超高值计算方法——双坡断面（x≤L 1）
AB
2i1
(
b 2
a)
(2a
b)i1
AC
xAB L1
x L1
(2a
b)i1
hw
x L1
(2a
b)i1
a(i2
i1)
hzh

ai2
b 2
i1
h 内= a i 2-（a+b jx）i 1
ai2
b 2 i1
h外 a(i2 i1) (2a b)i1 (a b)i1 ai2
x b jx Lc b j
超高值计算方法——旋转断面（X＞L 1）
ix
x Lc
ib
hw ai2 (a b)ix
hzh
ai2
b 2
ix
hn ai2 (a bjx )ix
x b jx Lc b j
超高值计算方法——起始段面
①起始断面：在超高缓和段起终点处，经提肩后， 形成的双坡断面：
h 中=a i 2+b i 1/ 2
h 内= h 外= a（ i 2- i 1）
超高值计算方法——双坡断面（x≤L 1）
缓和段上任意一点离开起点的距离为x，路肩边 缘由A升到C。（c点为超高渐变过程中从起始断面的A点逐
把路肩横坡度抬高到与路面相同的横坡， 即使路基顶面变成简单的双向横坡。
超高形成过程——双坡阶段
双坡阶段：
从进入超高缓和段开始，先保持路面内侧不 动，外侧绕路中线向上旋转到与内侧同坡，
这一过程称为双坡阶段。其所需的长度为双
坡阶段长度L1，根据超高渐变的要求，路拱 坡度变化也是按离开缓和段起点的距离呈正

铁路曲线超高计算例题铁路曲线通常由圆曲线和缓和曲线两部分组成，其中圆曲线主要用于转弯处，而缓和曲线则用于连接直线段与圆曲线。

超高是指列车在曲线中行驶时车身与轨道之间的垂直距离差，计算超高是铁路设计中的一项重要工作。

下面举一个例题进行计算：一条铁路线路，限速120公里/小时，列车长度200米，弯曲半径800米。

计算该曲线的超高值。

解题思路：根据铁路设计规定，车辆在曲线上行驶时需要满足一定的超高限制，以确保列车安全稳定。

为了计算出该曲线的超高值，首先需要确定列车在曲线的最大超高值。

1. 确定最大超高限制首先，根据铁路行车规定，列车在曲线上的最大超高值应为铁路限速值除以25，再加上1.5米。

因此，在本题中最大超高值为：MaxH = 120 / 25 + 1.5 = 6.5米2. 确定最大列车超高其次，需要根据列车长度和弯曲半径计算出列车在曲线上可能出现的最大超高值，以便确定超高是否符合安全要求。

根据铁路设计公式，列车在圆曲线上行驶时的最大超高可以用以下公式计算：Maxh = (L^2 / 24R) + (R/2)其中，L是列车长度，R是弯曲半径。

带入数据可得：Maxh = (200^2 / (24×800)) + (800/2) = 3.47米因此，该曲线上可能出现的最大超高值是3.47米。

3. 确定实际超高值最后，根据弯曲半径和曲线长度的关系，可以利用铁路设计公式计算出该曲线的实际超高值：H = (L/2) × (L/(24×R))带入数据可得：H = (200/2) × (200/(24×800)) = 0.65米因此，该曲线的超高值为0.65米，低于最大允许超高值6.5米，符合安全要求。

结论：通过计算，我们得出该曲线的超高值为0.65米，符合安全要求。

因此，该曲线可以使用，列车可以在曲线上正常通行。

（1）K17+525 缓和曲线（<HY，>ZH）
ZH = K17+512.895 HY = K 17+587.895
双坡阶段长度： x0iiG hL c00..001775 51.0 67
QZ = K17+626.273 YH = K17+664.651 HZ = K17+739.651
p 1iG x0 B0 .0 1.0 1 67 .7 50 .7 % 0 .3 %
路堑边坡坡度：应根据当地自然条件、土石种类及其结构、边坡高度 和施工方法等确定。
▪ 一般情况下，土质(包括粗粒土)挖方边坡坡度参照表5.4.8选用。一 般土质挖方边坡高度不宜超过30m。
5.5 道路建筑限界与道路用地范围
5.5.1 道路用地范围
1．公路用地范围： 填方地段为公路路堤两侧排水沟外边缘(无排水沟时为路堤或护坡道坡
ho1
(2 x x0
1)b1i1
ho2(2xx01)b (1b2)i1 ho3(2xx01)b (1b2b3)i1
旧《规范》：硬路肩宽度≥2.25m时，外侧路肩按向外侧倾斜。
h o 2 h o 1 b 2 i 2 , h o 3 h o 2 b 3 i 3
新《规范》：外侧土路肩按向外侧倾斜：ho3ho2b3i3
脚)以外、挖方地段为路堑坡顶截水沟外边缘(无截水沟为坡顶)以外，不小 于1m的土地为公路用地范围。
在有条件的地段，高速公路、一级公路不少于3m，二级公路不少于2m 的土地为公路用地范围。
高填深挖路段：应根据边坡稳定计算确定用地范围。 2．城市道路用地：
城市道路用地范围为城市道路红线宽度。
5.5 道路建筑限界与道路用地范围

-------------
-------------
注：括号值为路拱大于2%时的不设超高最小半径新的路线设计规范要求超高应该按照运行速度进行选取。

在进行运行速度计算后，根据这个公式反算
R=V2/127（f+i）
式中：V—运行速度(km/h)；
f—路面与轮胎间的横向力系数；
i—路面超高横坡度。

超高过渡段长度按下式计算：
LC = B △i/P
式中：LC —超高过渡段长度(m)；
-------------
B —旋转轴至行车道(设路缘带时为路缘带)外侧边缘的宽度(m)；
△i—超高坡度与路拱坡度的代数差(%)；
P —超高渐变率，即旋转轴与行车道(设路缘带时为路缘带) 外侧边缘线之间的相对坡度，其值如表7.5.4。

根据上式求得过渡段长度，应凑整成5m的倍数，并不小于20m的长度。

-------------。

～ 360 ～ 105 <360 ～ 230 <230 ～ 150 <150 ～ 90 <90 ～ 60 <105 ～ 70 <70 ～ 55 <55 40 <40 ～ 30 <30 ～ 20 <20 ～ 15
3
～ 2160 ～ 1290 ～ 1220 ～ 1050 <2160 <1290 <1220 ～ 950 <950 ～ 770 <770 ～ 650 <650 ～ 560 <560 ～ 500 <500 ～ 440 <440 ～ 400 <1050 ～ 760 <760 ～ 550 <550 ～ 400
(2)有中间带的公路
①绕中间带的中心线旋转。如图3－10 （a） 。 先将外侧行车道绕中间带的中心旋转，待达到与内侧行车道构成单向横坡后， 整个断面一同绕中心线旋转，直至超高横坡值。此时，中央分隔带呈倾斜状。采 用窄中间带的公路可选用此方式，或中间带宽度小于4.5m的可采用此种方式。 ②绕中央分隔带边缘旋转。如图3－10 （b） 。 将两侧行车道分别绕中央分隔带边缘旋转，使之各自成为独立的单向超高断 面，此时中央分隔带维持原水平状态。各种宽度不同的中间带均可选用此种方式。
B、 绕 中 线 旋 转 。 简 称 中 轴 旋 转 。 如 图 3－ 8。 在 超 高 缓 和 段 之 前 ， 先 将 路 肩 横 坡 逐 渐 变 为 路 拱 横 坡 ， 再 以 路 中 线 为 旋 转 轴 ， 使 外 侧 车 道 和 内 侧 车 道 变 为 单 向 的 横 坡 度 后 ，整 个 断 面 一 同 绕 中 线 旋 转 ，使 单 坡 横 断 面 直 至 达 到 超 高 横 坡 度 为 止 。 一 般 改 建 公 路 常 采 用 此 种 方 式 。

道路定线圆曲线计算公式
道路定线圆曲线是道路工程中常见的设计要素，它用于在道路
设计中确定道路的水平和垂直曲线。

在道路定线圆曲线设计中，我
们通常会用到以下几个公式：
1. 圆曲线半径（R）的计算公式：
R = (V^2) / (1279 f)。

其中，V为设计车速（单位，km/h），f为超高（单位，m）。

2. 圆曲线长度（L）的计算公式：
L = (R θ)。

其中，R为圆曲线半径（单位，m），θ为圆曲线的圆心角（单位，弧度）。

3. 圆曲线的过渡曲线长度（Ls）的计算公式：
Ls = (V^2) / (254 e)。

其中，V为设计车速（单位，km/h），e为过渡曲线的超高差（单位，m）。

这些公式是在道路设计中常用的计算公式，它们可以帮助工程师确定道路定线圆曲线的设计参数，确保道路的安全性和舒适性。

在实际应用中，还需要考虑到道路的地形、交通量、设计标准等因素，综合运用这些公式进行道路设计。

希望这些信息能够对你有所帮助。

曲线超高计算公式为:h=V⒉/Rh——外轨超高量.V——通过曲线时的列车速度km／h；R——曲线半径m;实际设置超高时,取其整数到5毫米,最大超高为150毫米.单线上下行速度悬殊时,不超过125毫米.计算公式适用于改建铁路;新建铁路推荐使用以下公式：h=⒉/R问题来了,原来的为什么变成了,那么这个新建铁路推荐公式是否可用还有个问题,缓和曲线内怎么顺完超高,例如现在有R=600,l=100缓和曲线长,L=曲线长,设计速度大概是60km/h吧,那么超高应该是多少,缓和曲线超高分段应该多少米我正矢是这么做的,圆曲线正矢Fc=50000/R=50000/600=83mm缓和曲线正矢递减率fs=Fc/n=83/10=8mm缓和曲线长l=100m,所以我n=10m,求出fzh=fhz=fs /6=1mm,中间点正矢=对应点fs;我现对你提出2个的问题分别作答,不对之处请斧正：1、实际上列车通过曲线的各次列车不尽相同,故准确表达式应为h=R为了反映不同行驶速度和不同牵引力重量的列车对外轨超高值的不同要求,均衡内外轨的垂直磨耗,平均速度V=√∑NGV2/∑NG其中N-每昼夜通过列车的相同速度和牵引重量的列车次数；G-列车总重;在新建线设计和施工中,采用的平均速度V′由下式确定V=Max故有： h=Max∧2/R mm其中VMax-预计该地段最大行车速度,以Km/h计;2、不知道其他地方是怎么处理的,沪宁线的缓和曲线段内的超高设置相对比较简单,因为公式中R在缓和曲线段一直是变化的且R均比较大,所以设计院为了简化这个问题,一般采用从直线段0超高到圆曲线段超高即超高最大,直线渐变的形式处理,即缓和曲线上i点的超高 hi =h′Li/L其中Li-i点所在位置的曲线长L-缓和曲线长h′-圆曲线段超高值希望能对你有所帮助。

1
2
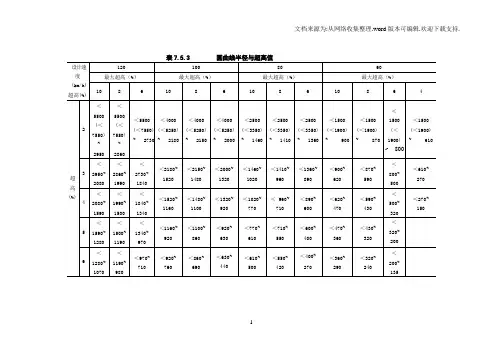
注：括号值为路拱大于2%时的不设超高最小半径
新的路线设计规范要求超高应该按照运行速度进行选取。

在进行运行速度计算后，根据这个公式反算
R=V2/127（f+i）
式中：V—运行速度(km/h)；
f—路面与轮胎间的横向力系数；
i—路面超高横坡度。

超高过渡段长度按下式计算：
LC = B △i/P
式中：LC —超高过渡段长度(m)；
B —旋转轴至行车道(设路缘带时为路缘带)外侧边缘的宽度(m)；
△i—超高坡度与路拱坡度的代数差(%)；
P —超高渐变率，即旋转轴与行车道(设路缘带时为路缘带) 外侧边缘线之间的相对坡度，其值如表根据上式求得过渡段长度，应凑整成5m的倍数，并不小于20m的长度。

3。

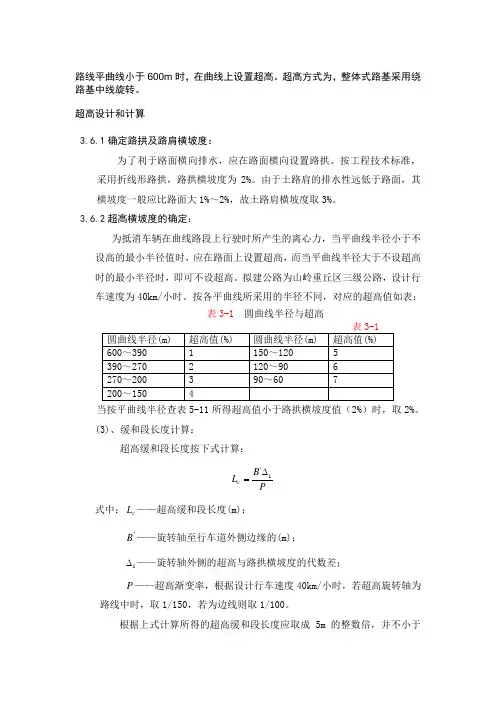
路线平曲线小于600m 时，在曲线上设置超高。

超高方式为，整体式路基采用绕路基中线旋转。

超高设计和计算3.6.1确定路拱及路肩横坡度：为了利于路面横向排水，应在路面横向设置路拱。

按工程技术标准，采用折线形路拱，路拱横坡度为2%。

由于土路肩的排水性远低于路面，其横坡度一般应比路面大1%～2%，故土路肩横坡度取3%。

3.6.2超高横坡度的确定：为抵消车辆在曲线路段上行驶时所产生的离心力，当平曲线半径小于不设高的最小半径值时，应在路面上设置超高，而当平曲线半径大于不设超高时的最小半径时，即可不设超高。

拟建公路为山岭重丘区三级公路，设计行车速度为40km/小时。

按各平曲线所采用的半径不同，对应的超高值如表： 表3-1 圆曲线半径与超高 圆曲线半径(m) 超高值(%) 圆曲线半径(m) 超高值(%) 600～390 1 150～120 5 390～270 2 120～90 6 270～200 3 90～60 7 200～150 4 当按平曲线半径查表5-11所得超高值小于路拱横坡度值（2%）时，取2%。

(3)、缓和段长度计算：超高缓和段长度按下式计算：PB L c i'∆=式中：c L ——超高缓和段长度(m)；'B ——旋转轴至行车道外侧边缘的(m)； i ∆——旋转轴外侧的超高与路拱横坡度的代数差；P ——超高渐变率，根据设计行车速度40km/小时，若超高旋转轴为路线中时，取1/150，若为边线则取1/100。

根据上式计算所得的超高缓和段长度应取成5m 的整数倍，并不小于10m 的长度。

拟建公路为无中间带的三级公路，则上式中各参数的取值如下：绕行车道中心旋转：z y i i BB +=∆=i ' , 2绕边线旋转：y i B B =∆=i ' ,式中：B ——行车道宽度(m)； y i ——超高横坡度； z i ——路拱横坡度。

(4)、超高缓和段的确定：超高缓和段长主要从两个方面来考虑：一是从行车舒适性来考虑，缓和段长度越长越好；二是从排水来考虑，缓和段越短越好，特别是路线纵坡度较小时，更应注意排水的要求。

1超高的设计有几种，有的按渐变率确定超高渐变段的长度的;有的设计是按内插法计算超高横坡，有的是按三次抛物线计算超高横坡.据我个人的经验，珠三角地区一般都有三次抛物线的超高设计出现，但上面的计算方法它会列出计算的公式.
2下面这种方法可能叫超高渐变率
B是旋转轴到行车道外侧边缘的宽度。

ix=(ig+ih)*x/Lc-ig。

ig为路拱横坡值，ih为超高横坡度，x为超高缓和段中任意一点至超高缓和段起点的距离。

Lc为最下超高过渡段长度。

路线上每个缓和曲线都换有个超高渐变率，L（要求点到直缓点的距离）i1（直线段横坡），i2（圆曲线上的超高横坡）i（要求点横坡），i=i1+LP，P（超高渐变率）=（i2-i1）/l，l（缓和曲线上度）
3,4800超高计算程序
Lbl 1:”N(1-2)”:A”I1”:B”I2“：C”K1“：D”K2“：{K｝：K>D=＞Goto 9△K<C=＞Goto 9△
N=1=＞Goto 3△N=2=＞Goto 2△
Lbl 2:X=K-C:L=D-C
I=A+（2X÷L-3）×（（A-B）X2÷L2
Goto 4
Lbl 3：E=（B-A）÷（D-C）
D<0=＞E=-E△
I=A+(K-C)E
Lbl 4:”I=”:I◢
Goto 1
Lbl 9:”END”
给条程序给你4800的，
（1-2）。

1线型。

2三次抛物线
I1。

起点横坡
I2。

终点横坡
K1。

起点桩号
K2。

终点桩号K。

所求桩号。

公路等级地区计算车速超高1超高2超高3超高4超高5超高6超高7超高8超高9超高10半径超高差绕中线超高渐变率行车道+硬路肩缓和曲线最小长度高速公路最大超高10%120550029502080159012801070910790680570400041/25011.75117.5高速公路最大超高8%1205500286019901500119098079065000高速公路最大超高6%12055002730184013409707100000高速公路积雪冰冻地区120550027801910141010708100000高速公路最大超高10%1004000218015201160920760640540450360高速公路最大超高8%100400021501480110086069053040000高速公路最大超高6%1004000200013209206304400000高速公路积雪冰冻地区10040002090141010407705650000高速公路最大超高10%80250014601020770610500410340280220高速公路最大超高8%802500141096071055042032025000高速公路最大超高6%80250013608906004002700000高速公路积雪冰冻地区80250013909406804903600000一级公路最大超高10%1004000218015201160920760640540450360一级公路最大超高8%100400021501480110086069053040000一级公路最大超高6%1004000200013209206304400000一级公路积雪冰冻地区10040002090141010407705650000一级公路最大超高10%80250014601020770610500410340280220一级公路最大超高8%802500141096071055042032025000一级公路最大超高6%80250013608906004002700000一级公路积雪冰冻地区80250013909406804903600000一级公路最大超高10%601500900620470360290240190150115一级公路最大超高8%60150087059043032024017012500一级公路最大超高6%6015008005003202001350000一级公路最大超高4%601500610270150000000一级公路积雪冰冻地区6015008605704102902050000二级公路最大超高10%80250014601020770610500410340280220二级公路最大超高8%802500141096071055042032025000二级公路最大超高6%80250013608906004002700000二级公路积雪冰冻地区80250013909406804903600000二级公路最大超高10%601500900620470360290240190150115二级公路最大超高8%6015008705904303202401701250040071/175898.0二级公路最大超高6%6015008005003202001350000二级公路最大超高4%601500610270150000000二级公路积雪冰冻地区6015008605704102902050000三级公路最大超高8%4060047031022016012080550032851/150 3.526.3三级公路最大超高6%4060041025015090600000三级公路最大超高4%4060033013070000000三级公路最大超高2%406007500000000三级公路积雪冰冻地区40600430280190130900000三级公路最大超高8%30350250170120906040300030101/125 3.543.8三级公路最大超高6%303502301408050350000三级公路最大超高4%303501506035000000三级公路最大超高2%303504000000000三级公路积雪冰冻地区3035027018012090550000四级公路最大超高8%20150140907050403015006071/100 3.524.5四级公路最大超高6%20150110704030150000四级公路最大超高4%20150703015000000四级公路最大超高2%201502000000000四级公路积雪冰冻地区20150120806040250000缓和曲线最小长度155.1184.857.8115.580.9。

路线平曲线小于600m时，在曲线上设置超高。

超高方式为，整体式路基采用绕路基中线旋转。

超高设计和计算361确定路拱及路肩横坡度：为了利于路面横向排水，应在路面横向设置路拱。

按工程技术标准，采用折线形路拱，路拱横坡度为2%由于土路肩的排水性远低于路面，其横坡度一般应比路面大1%-2%故土路肩横坡度取3%362超高横坡度的确定：为抵消车辆在曲线路段上行驶时所产生的离心力，当平曲线半径小于不设高的最小半径值时，应在路面上设置超高，而当平曲线半径大于不设超高时的最小半径时，即可不设超高。

拟建公路为山岭重丘区三级公路，设计行车速度为40km/小时。

按各平曲线所采用的半径不同，对应的超高值如表：表3-1圆曲线半径与超高表3-1当按平曲线半径查表5-11所得超高值小于路拱横坡度值(2%时，取2%(3)、缓和段长度计算：超高缓和段长度按下式计算：,B，\L cP式中：L c——超高缓和段长度(m);B ------ 旋转轴至行车道外侧边缘的(m);i――旋转轴外侧的超高与路拱横坡度的代数差；P——超高渐变率，根据设计行车速度40km/小时，若超高旋转轴为路线中时，取1/150，若为边线则取1/100根据上式计算所得的超高缓和段长度应取成5m的整数倍，并不小于10m的长度。

拟建公路为无中间带的三级公路，则上式中各参数的取值如下：绕行车道中心旋转：B‘ = B ,冷=i y i z2绕边线旋转：B^B , . ^-i y式中：B ――行车道宽度(m)；i y ――超高横坡度；i z ――路拱横坡度。

(4)、超高缓和段的确定：超高缓和段长主要从两个方面来考虑：一是从行车舒适性来考虑，缓和段长度越长越好；二是从排水来考虑，缓和段越短越好，特别是路线纵坡度较小时，更应注意排水的要求。

3.6.3确定缓和段长度时应考虑以下几点：⑴、一般情况下，取缓和段长度和缓和曲线长相等，即L c = L s，使超高过渡在缓和曲线全长范围内进行。

注：括号值为路拱大于2%时的不设超高最小半径
新的路线设计规范要求超高应该按照运行速度进行选取。

在进行运行速度计算后，根据这个公式反算
R=V2/127（f+i）
式中：V—运行速度(km/h)；
f—路面与轮胎间的横向力系数；
i—路面超高横坡度。

超高过渡段长度按下式计算：
LC = B △i/P
式中：LC —超高过渡段长度(m)；
B —旋转轴至行车道(设路缘带时为路缘带)外侧边缘的宽度(m)；
△i—超高坡度与路拱坡度的代数差(%)；
P —超高渐变率，即旋转轴与行车道(设路缘带时为路缘带) 外侧边缘线之间的相对坡度，其值如表7.5.4。

根据上式求得过渡段长度，应凑整成5m的倍数，并不小于20m的长度。

半径 灵 活地设 置超 高数 值 。
ｆ ＜ ０ ． １ ０时 ， 不感 到有曲线存在 ， 很平稳 ；
ｆ ＝ ０ ． １ ５时 ， 略感 到 有 曲线 存在 ， 但 尚平稳 ； ｆ ＝ ０ ． ２ ０时 ， 已感 到 有 曲线 存 在 ， 并 感到 不平 稳 ；
ｆ ＝ ０ ． ３ ５时 ， 感 到有 曲线存 在 ， 并感 到不平 稳 ；
笔 者 近年 来 查 阅 国 内的相 关 论文 与书 籍 ， 并 没
有找到平 曲线半径与超高数值的对应计算关系。但
是在 国外 的相 关 资料 中 ， 有 关 于 圆 曲线 半 径 与 超 高 值 的计算 方法 ， 本论 文将 介绍 《 Ａ Ｐ ｏ ｌ ｉ ｃ ｙ ｏ ｎ Ｇ ｅ ｏ ｍｅ ｔ ｉ ｒ ｃ Ｄ ｅ ｓ ｉ ｇ ｎ ｏ ｆ Ｈ ｉ ｇ ｈ ｗ ａ ｙ ｓ ａ ｎ ｄ Ｓ ｔ ｒ ｅ ｅ ｔ ｓ ｝（ Ａ Ａ Ｓ Ｈ Ｔ Ｏ ２ ０ ０ １ ） 中
时， 横 向力 系数与乘 客感 觉 的关 系如下 ：
４ ｅ或 ｆ 在 曲线 范 围的分 配 对 于某 一既 定 的设 计 速度 ， 采 用 ｅ或 ｆ 或 两 者
来 抵消行 驶 在 曲线 上 的离心 力 ， 共 有 ５中方 法 ， 得 出
２ ０ １ ４年
第１ ０期
卢艳 坤 ： 公路设计 中圆曲线超高值 的计算方 法分 析
（ １ ） 方 法一 ： 图 １ 各 图 中所 示 的① 表 超 高或 ０ 鲁 ｏ 暑 ＞ 主 ～ ａ ｄ ｊ ∞ 量童 ， 口 ０ 示 ｕ Ｊ Ｐ ｌ ｓ ●
／
／ ／
，
’
／
，
ａ ｔ ｄ ｅ ｓ ｊ 嚣 船
５
一 ，
，
一 加

圆曲线半径与超高值表7.5.3圆曲线半径与超高值
注：括号值为路拱大于2%时的不设超高最小半径新的路线设计规范要求超高应该按照运行速度进行选取。

在进行运行速度计算后，根据这个公式反算
R=V2/127（f+i）
式中：V—运行速度(km/h)；
f—路面与轮胎间的横向力系数；
i—路面超高横坡度。

超高过渡段长度按下式计算：
LC = B △i/P
式中：LC —超高过渡段长度(m)；
B —旋转轴至行车道(设路缘带时为路缘带)外侧边缘的宽度(m)；
△i—超高坡度与路拱坡度的代数差(%)；
P —超高渐变率，即旋转轴与行车道(设路缘带时为路缘带) 外侧边缘线之间的相对坡度，其值如表7.5.4。