圆曲线半径与超高值

铁路曲线超高计算例题铁路曲线通常由圆曲线和缓和曲线两部分组成，其中圆曲线主要用于转弯处，而缓和曲线则用于连接直线段与圆曲线。

超高是指列车在曲线中行驶时车身与轨道之间的垂直距离差，计算超高是铁路设计中的一项重要工作。

下面举一个例题进行计算：一条铁路线路，限速120公里/小时，列车长度200米，弯曲半径800米。

计算该曲线的超高值。

解题思路：根据铁路设计规定，车辆在曲线上行驶时需要满足一定的超高限制，以确保列车安全稳定。

为了计算出该曲线的超高值，首先需要确定列车在曲线的最大超高值。

1. 确定最大超高限制首先，根据铁路行车规定，列车在曲线上的最大超高值应为铁路限速值除以25，再加上1.5米。

因此，在本题中最大超高值为：MaxH = 120 / 25 + 1.5 = 6.5米2. 确定最大列车超高其次，需要根据列车长度和弯曲半径计算出列车在曲线上可能出现的最大超高值，以便确定超高是否符合安全要求。

根据铁路设计公式，列车在圆曲线上行驶时的最大超高可以用以下公式计算：Maxh = (L^2 / 24R) + (R/2)其中，L是列车长度，R是弯曲半径。

带入数据可得：Maxh = (200^2 / (24×800)) + (800/2) = 3.47米因此，该曲线上可能出现的最大超高值是3.47米。

3. 确定实际超高值最后，根据弯曲半径和曲线长度的关系，可以利用铁路设计公式计算出该曲线的实际超高值：H = (L/2) × (L/(24×R))带入数据可得：H = (200/2) × (200/(24×800)) = 0.65米因此，该曲线的超高值为0.65米，低于最大允许超高值6.5米，符合安全要求。

结论：通过计算，我们得出该曲线的超高值为0.65米，符合安全要求。

因此，该曲线可以使用，列车可以在曲线上正常通行。

公路平曲线设计中的超高设计作者：王敬一刘亚来源：《科技资讯》 2011年第26期摘要：本文结合商丘市内连接飞机场的二级公路改建工程，对公路超高计算过程进行了详细的说明，着重分析了超高值、超高缓和段长度及计算参数等的确定方法，阐明了设计计算的过程。

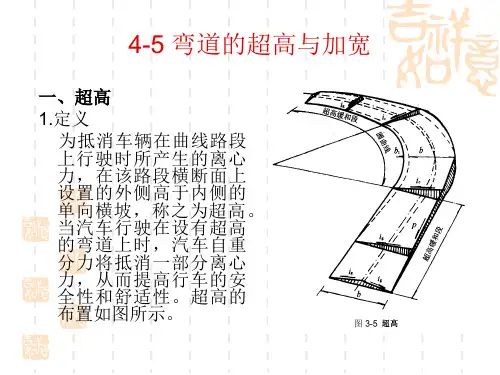
关键词：超高超高渐变率超高缓和段在弯道上，当车辆行驶在双向横坡的车道外侧时，车重的水平分力将增大车辆的横向侧滑力，所以当采用的圆曲线半径小于不设超高的最小半径时，为抵消车辆在曲线路段上行驶时所产生的离心力，保证车辆的稳定性和舒适性，将曲线段上的路面做成外侧高于内侧的单向横坡的形式以全部或部分抵消车辆所受的离心力，这就是路面超高。

超高的设计包括超高值的确定、超高过渡方式、缓和段的长度及超高渐变率的取值等关键问题。

本文将结合商丘市内一连接飞机场的二级公路改造工程对超高设计计算中的一些具体环节进行说明。

1 工程概况本项目为旧路改造工程，原有道路为县乡道路，为三、四级公路，路基宽度10，路面宽度7ｍ，改建后其技术标准为双向单车道二级公路，设计速度采用80m/h，路基宽度15m，路面宽度12m，路拱横坡为2%，土路肩横坡为3%，无中央分隔带。

由于需要，需在处设置超高，超高值确定为4%，圆曲线半径为800m。

2 超高值的确定本项目路线按照二级路标准设计，设计车速为80Km/h，路线设计时采用的圆曲线半径为800m，小于规范规定的不设超高的最小半径2500m，因此在此段需要设置超高。

需要采用的超高值按照下式计算确定。

式中：——计算行车速度（Km/h），本文采用设计车速80Km/h；——圆曲线半径（m），本文采用800m；——横向力系数公式中的和都好确定，就不再做赘述。

这里主要讲一下横向力系数μ的取值。

影响μ取值的因素比较多，不同教材上对其取值的计算方法也有多种，不尽相同。

本文兼顾计算的方便性和结果与规范的一致性，决定利用规范给出的三组特征半径和μ的对应值进行拟合，得到任意半径值下的μ的计算公式。

-------------
-------------
注：括号值为路拱大于2%时的不设超高最小半径新的路线设计规范要求超高应该按照运行速度进行选取。

在进行运行速度计算后，根据这个公式反算
R=V2/127（f+i）
式中：V—运行速度(km/h)；
f—路面与轮胎间的横向力系数；
i—路面超高横坡度。

超高过渡段长度按下式计算：
LC = B △i/P
式中：LC —超高过渡段长度(m)；
-------------
B —旋转轴至行车道(设路缘带时为路缘带)外侧边缘的宽度(m)；
△i—超高坡度与路拱坡度的代数差(%)；
P —超高渐变率，即旋转轴与行车道(设路缘带时为路缘带) 外侧边缘线之间的相对坡度，其值如表7.5.4。

根据上式求得过渡段长度，应凑整成5m的倍数，并不小于20m的长度。

-------------。

《公路设计》超高问题基本流程：超高一般的设计过程是:第一,确定超高的横坡坡度;第二,查《路线规范》超高渐变率表试定超高渐变率;第三,按照公式Lc = B Δi / p 计算超高缓和段长度;第四,将凑整后的超高缓和段长度代入上式,反算超高渐变率。

以一道例题作为计算例子：一、相关技术指标1．二级公路，设计速度60 km/h ；2．行车道宽2×4.5 m ，土路肩2×0.50 m ；3．行车道路拱横坡度1.5%，土路肩路拱横坡度2.5%；4．不设超高的圆曲线最小半径1500m ；圆曲线最大超高值8%；5．超高过渡方式：绕内侧车道边缘旋转。

二、超高过渡段长度计算公式p i B L c D = ()c c c g c Bi L p B i i L p ì=ïïí+ï=ïî绕边轴旋转绕中线旋转 （1） 式中：c L ——最小超高过渡段长度（m ）；B ——旋转轴至行车道（设路缘带时为路缘带）外侧边缘的宽度（m ）；i D ——超高横坡度与路拱横坡度的代数差（%）；p ——超高渐变率（m ）；c i ——超高横坡度（%）；g i ——路拱横坡度（%）。

三、超高过渡段长度的确定1．计算最小超高过渡段长度c c Bi L p= （1251=p ，m B 9=） 用计算出的c L 与回旋线长度s L 比较，由于平面设计时已经考虑了超高过渡的需要，所以一般情况下计算出的s c L L £，故先取s c L L =；否则应考虑修改平面线形或采取其他措施。

2．计算横坡由双向路拱横坡（-1.5%）过渡到单向超高横坡（1.5%）时的超高渐变率p由公式（1）反算：()''002g g g B i i B i p x x éù--×ëû== （绕中线旋转，m B 5.4'=， 1.5%g i =） 0g c ci x L i = （临界断面） 3．超高过渡段长度的确定（1）若3301³p ，则取s c L L =，即超高过渡在缓和曲线全长范围内进行； （2）若3301<p ，按以下两种方法处理： 1）在缓和曲线部分范围内超高即超高过渡起点可从缓和曲线起点（¥=R ）至缓和曲线上不设超高的最小半径之间的任一点开始，至缓和曲线终点结束。

曲线超高计算公式为:h=V⒉/Rh——外轨超高量.V——通过曲线时的列车速度km／h；R——曲线半径m;实际设置超高时,取其整数到5毫米,最大超高为150毫米.单线上下行速度悬殊时,不超过125毫米.计算公式适用于改建铁路;新建铁路推荐使用以下公式：h=⒉/R问题来了,原来的为什么变成了,那么这个新建铁路推荐公式是否可用还有个问题,缓和曲线内怎么顺完超高,例如现在有R=600,l=100缓和曲线长,L=曲线长,设计速度大概是60km/h吧,那么超高应该是多少,缓和曲线超高分段应该多少米我正矢是这么做的,圆曲线正矢Fc=50000/R=50000/600=83mm缓和曲线正矢递减率fs=Fc/n=83/10=8mm缓和曲线长l=100m,所以我n=10m,求出fzh=fhz=fs /6=1mm,中间点正矢=对应点fs;我现对你提出2个的问题分别作答,不对之处请斧正：1、实际上列车通过曲线的各次列车不尽相同,故准确表达式应为h=R为了反映不同行驶速度和不同牵引力重量的列车对外轨超高值的不同要求,均衡内外轨的垂直磨耗,平均速度V=√∑NGV2/∑NG其中N-每昼夜通过列车的相同速度和牵引重量的列车次数；G-列车总重;在新建线设计和施工中,采用的平均速度V′由下式确定V=Max故有： h=Max∧2/R mm其中VMax-预计该地段最大行车速度,以Km/h计;2、不知道其他地方是怎么处理的,沪宁线的缓和曲线段内的超高设置相对比较简单,因为公式中R在缓和曲线段一直是变化的且R均比较大,所以设计院为了简化这个问题,一般采用从直线段0超高到圆曲线段超高即超高最大,直线渐变的形式处理,即缓和曲线上i点的超高 hi =h′Li/L其中Li-i点所在位置的曲线长L-缓和曲线长h′-圆曲线段超高值希望能对你有所帮助。

1
2
注：括号值为路拱大于2%时的不设超高最小半径
新的路线设计规范要求超高应该按照运行速度进行选取。

在进行运行速度计算后，根据这个公式反算
R=V2/127（f+i）
式中：V—运行速度(km/h)；
f—路面与轮胎间的横向力系数；
i—路面超高横坡度。

超高过渡段长度按下式计算：
LC = B △i/P
式中：LC —超高过渡段长度(m)；
B —旋转轴至行车道(设路缘带时为路缘带)外侧边缘的宽度(m)；
△i—超高坡度与路拱坡度的代数差(%)；
P —超高渐变率，即旋转轴与行车道(设路缘带时为路缘带) 外侧边缘线之间的相对坡度，其值如表根据上式求得过渡段长度，应凑整成5m的倍数，并不小于20m的长度。

3。

公路圆曲线半径与超高值
公路圆曲线的半径和超高值之间存在一定的关系。

在公路设计中，圆曲线的半径是决定超高值的重要因素之一。

一般来说，圆曲线的半径越小，超高值就越大。

这是因为当半径较小时，车辆在曲线行驶时需要更大的向心力来平衡离心力，因此需要更高的超高值来确保车辆行驶的稳定性和安全性。

另外，超高值的设计还需要考虑公路等级、所处区域等因素。

不同的公路等级和区域会有不同的超高值规定。

例如，在积雪冰冻地区，圆曲线的最大超高值通常为6%，而在一般地区则为8%。

在超高值的设计过程中，还需要考虑横向摩阻力的影响。

横向摩阻力是影响车辆行驶稳定性和舒适性的重要因素之一。

因此，在超高值的设计中，需要将横向摩阻力减至最低程度，以确保车辆行驶的稳定性和舒适性。

总之，公路圆曲线的半径和超高值之间存在密切的关系，需要根据公路等级、所处区域等因素进行综合考虑和设计。

路线平曲线小于600m时，在曲线上设置超高。

超高方式为，整体式路基采用绕路基中线旋转。

超高设计和计算361确定路拱及路肩横坡度：为了利于路面横向排水，应在路面横向设置路拱。

按工程技术标准，采用折线形路拱，路拱横坡度为2%由于土路肩的排水性远低于路面，其横坡度一般应比路面大1%-2%故土路肩横坡度取3%362超高横坡度的确定：为抵消车辆在曲线路段上行驶时所产生的离心力，当平曲线半径小于不设高的最小半径值时，应在路面上设置超高，而当平曲线半径大于不设超高时的最小半径时，即可不设超高。

拟建公路为山岭重丘区三级公路，设计行车速度为40km/小时。

按各平曲线所采用的半径不同，对应的超高值如表：表3-1圆曲线半径与超高表3-1当按平曲线半径查表5-11所得超高值小于路拱横坡度值(2%时，取2%(3)、缓和段长度计算：超高缓和段长度按下式计算：,B，\L cP式中：L c——超高缓和段长度(m);B ------ 旋转轴至行车道外侧边缘的(m);i――旋转轴外侧的超高与路拱横坡度的代数差；P——超高渐变率，根据设计行车速度40km/小时，若超高旋转轴为路线中时，取1/150，若为边线则取1/100根据上式计算所得的超高缓和段长度应取成5m的整数倍，并不小于10m的长度。

拟建公路为无中间带的三级公路，则上式中各参数的取值如下：绕行车道中心旋转：B‘ = B ,冷=i y i z2绕边线旋转：B^B , . ^-i y式中：B ――行车道宽度(m)；i y ――超高横坡度；i z ――路拱横坡度。

(4)、超高缓和段的确定：超高缓和段长主要从两个方面来考虑：一是从行车舒适性来考虑，缓和段长度越长越好；二是从排水来考虑，缓和段越短越好，特别是路线纵坡度较小时，更应注意排水的要求。

3.6.3确定缓和段长度时应考虑以下几点：⑴、一般情况下，取缓和段长度和缓和曲线长相等，即L c = L s，使超高过渡在缓和曲线全长范围内进行。

注：括号值为路拱大于2%时的不设超高最小半径
新的路线设计规范要求超高应该按照运行速度进行选取。

在进行运行速度计算后，根据这个公式反算
R=V2/127（f+i）
式中：V—运行速度(km/h)；
f—路面与轮胎间的横向力系数；
i—路面超高横坡度。

超高过渡段长度按下式计算：
LC = B △i/P
式中：LC —超高过渡段长度(m)；
B —旋转轴至行车道(设路缘带时为路缘带)外侧边缘的宽度(m)；
△i—超高坡度与路拱坡度的代数差(%)；
P —超高渐变率，即旋转轴与行车道(设路缘带时为路缘带) 外侧边缘线之间的相对坡度，其值如表7.5.4。

根据上式求得过渡段长度，应凑整成5m的倍数，并不小于20m的长度。

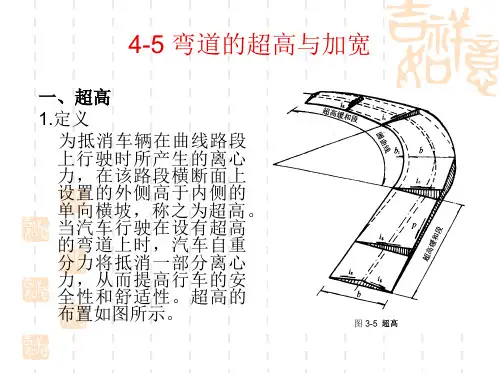
位于曲线上的行车道、硬路肩，均应根据设计速度、圆曲线半径、自然条件等按表7.5.3规定设置超高表7.5.3 圆曲线半径与超高值表7.5.3 (续)圆曲线半径与超高值超高过渡段由直线段的双向路拱横断面逐渐过渡到圆曲线段的全超高单向横断面，其间必须设置超高过渡段。

超高过渡段长度按公式（7.5.4）计算：B △ iL C =（7.5.4）P式中：L C —超高过渡段长度（m ）；B —旋转轴至行车道（设路缘带时为路缘带）外侧边缘的宽度（m ）；△ i —超高坡度与路拱坡度的代数差（％）；P —超高渐变率，即旋转轴与行车道（设路缘带时为路缘带）外侧边缘线之间的相对坡度，其值如表 根据上式求得过渡段长度，应凑整成 5m 的倍数，并不小于20m 的长度。

7.5.47.5.4。

7.5.5 超高过渡方式1 无中间带的公路（1）超高横坡度等于路拱坡度时，将外侧车道绕路中线旋转，直至超高横坡度。

（2）超高横坡度大于路拱坡度时，可分别采用以下三种过渡方式：1）绕车道内侧边缘旋转（见图7.5.5-1a）先将外侧车道绕路中线旋转，待达到与内侧车道构成单向横坡后，整个断面再绕未加宽前的内侧车道边缘旋转，直至超高横坡度一般新建工程应采用此种方式。

2）绕路中线旋转（见图7.5.5-1b）先将外侧车道绕路中线旋转，待达到与内侧车道构成单向横坡后，整个断面一同绕路中线旋转，直至超高横坡度。

一般改建工程应采用此种方式。

3）绕车道外侧边缘旋转（见图7.5.5-1c）先将外侧车道绕车道外侧边缘旋转，与此同时，内侧车道随中线的降低而相应降坡，待达到单向横坡后，整个断面继续绕外侧车道边缘旋转，直至超高横坡度。

此种方式可在特殊设计（如强调路容美观）时采用。

7.5.6 超高的过渡应在回旋线全长范围内进行。

当回旋线较长时，应采取以下措施予以处理：1 超高过渡段设在回旋线的某一区段内，其超高起点宜设在曲率半径大于不设超高半径处，全超高断面宜设在缓圆点和圆缓点处2 超高过渡段的纵向渐变率不得小于1/330 。

圆曲线超高率取值计算摘要：论述了超高率和摩擦系数的分配方法，分析了各种分配方法的优缺点。

提出了超高率取值设计的计算方法并探讨了纵坡对超高的影响，提出了超高率的取值应根据公路纵坡进行调整。

关键词：公路工程超高率摩擦系数纵坡影响1概述近年来，随着我国的公路建设的迅猛发展，灵活性设计理念已深入人心，超高计算取值则是其中的一个重要体现。

本文在超高率和摩擦系数抵消车辆在曲线路段上行驶时所产生的离心力的分配原则为基础，对公路圆曲线上超高率的取值进行了定量与定性相结合的分析。

2超高率和横向摩擦系数在曲线范围内的分配2.1分配的方法对某一既定的设计速度，可采用超高或横向摩擦系数或同时采用两者，以平衡车辆行驶在曲线上时所受的离心力，具体有以下五种方法[1]如图1所示。

方法①：超高e和横向摩擦系数f与平曲线曲率成正比（即在1/R=0和1/R=1/Rmax之间的直线关系）。

方法②：以设计速度行驶的汽车在未达到fmax的曲线上时，其离心力完全由横向摩擦力平衡。

当曲线曲率增大时，待摩擦力达到fmax并保持不变，剩余的离心力则由超高来平衡，直至e达到emax。

方法③：以设计速度行驶的汽车在未达到emax的曲线上，其离心力完全由曲线的超高来平衡。

当曲率再大时，超高达到emax并保持不变，这时剩余的离心力是由正比于曲率的横向摩擦力来平衡，直至f达到fmax。

方法④：以运行速度代替设计速度，其余与方法③相同。

方法⑤：认为超高率和横向摩擦系数与曲率成曲线关系，它们的值是介于方法①和方法③所得到的值。

2.2各方法分析比较方法①得出的超高率与曲率的直线关系，计算简单，具有相当的价值而又合乎逻辑。

但该分配方法要求车流中的每辆汽车都是以均速状态行驶，虽然大多数驾驶员都希望以均速行驶，但是只有在交通量不大，设计得很好的公路上才能实现均速行驶，而实际的道路状况往往不是这样，在实际中采用的超高率往往比此方法确定的e值要大，另外使用这种方法，在相当一部分曲线范围内是不用设置最大超高的。