当前位置：文档之家 › 数学建模实例ppt课件

数学建模实例ppt课件

  • 格式：ppt
  • 大小：1.24 MB
  • 文档页数：66

下载文档原格式

  / 66

合集下载

数学建模-第四篇-典型案例分析课件

数学建模-第四篇-典型案例分析课件

问题
☞ (1)请制定一个主管道钢管的订购和运输计 划, 使总费用最小（给出总费用).
☞ (2)请就(1)的模型分析: 哪个钢厂钢管的销 价的变化对购运计划和总费用影响最大，哪个 钢厂钢管的产量的上限的变化对购运计划和总 费用的影响最大，并给出相应的数字结果.
☞ (3)如果要铺设的管道不是一条线, 而是一 个树形图, 铁路、公路和管道构成网络, 请就 这种更一般的情形给出一种解决办法, 并对图 二按(1)的要求给出模型和结果.
§2.4 流量估计 1. 拟合水位~时间函数.
2. 确定流量~时间函数.
3. 一天总用水量的估计.
§2.5 算法设计与编程
1．拟合第1.2时段的水位，并导出流量.
2. 拟合供水时段的流量.
3. 一天总用水量的估计. 4. 流量及总用水量的检验.
Watertower.m
32Biblioteka 302826
24
22
20
★ 空气阻力的影响 对不同出手速度和出手高度的出手角度和入射角度
v(m/s）
8.0 8.5 9.0
h (m)
1.8 1.9 2.0 2.1
1.8 1.9 2.0 2.1
1.8 1.9 2.0 2.1
1度
2度
60.7869 61.6100 62.3017 62.9012
43.5424 41.5693 39.7156 37.9433
§1.2 问题的分析 d
d
球心偏前
0
△x
0 D
篮球入框
D
☞不考虑篮球和篮框大小,讨论球心命中框心的条件 ☞考虑篮球和篮框大小,讨论球心命中框心且入框条件 ☞保证球入框,出手角度和出手速度允许的最大偏差 ☞考虑空气阻力的影响

数学建模入门PPT课件

数学建模入门PPT课件
y
•
a
o
•
•
b
x
CHENLI
19
4 模型求解
证明： 将椅子转动 ，对角线互换，由
2
g(0)0,f(0)0,可得
f()0,g()0,
2
2
令 h ( ) f ( ) g ( )则 , h ( 0 ) f ( 0 ) g ( 0 ) 0 ,
4）按建立模型的数学方法（或所属数学分支）分类： 初等模型、几何模型、线性代数模型、微分方程模型、 图论模型、马氏链模型、运筹学模型等。
CHENLI
13
5）按建模目的分类： 描述性模型、分析模型、预报模型、优化模型、 决策模型、控制模型等。
6）按对模型结构的了解程度分类：
白箱模型：其内在机理相当清楚的学科问题，包括 力学、热学、电学等。
优决策控制等。
6）模型检验： 把模型分析的结果“翻译”回到实 际对象中，用实际现象、数据等检验模型的合理性 和适应性检验结果有三种情况：符合好，不好，阶 段性和部分性符合好。 7）模型应用：应用中可能发现新问题，需继续完善。
CHENLI
11
模型的分类
1）按变量的性质分类：
离散模型 确定性模型 线性模型 单变量模型 连续模型 随机性模型 非线性模型 多变量模型
•要有严密的数学推理，模型本身要正确；
•要有足够的精确度。
4）模型求解：可以包括解方程、画图形、证明定理
以及逻辑运算等。会用到传统的和近代的数学方
法，计算机技术（编程或软件包）。特别地近似计
算方法（泰勒级数，三角级数，二项式展开、代数
近似、有效数字等）。
CHENLI
10
5）模型分析：结果分析、数据分析。 变量之间的依赖关系或稳定性态；数学预测；最

《数学建模案例》课件

《数学建模案例》课件
《数学建模案例》PPT课 件
本课程将带你深入了解数学建模的基本概念、流程和方法，并通过真实案例 解析，帮助你实战体验数学建模的魅力。
数学建模的基本概念
定义
数学建模是用数学工具和方法研究现实问题，提出数学模型、进行分析和求解的过程。
意义
数学建模可以帮助我们理解和解决复杂实际问题，并为决策提供科学依据。
存在的问题和挑战
数学建模面临数据获取、模型不确定性和求解难 题等挑战。
重要性
数学建模是培养创新思维、科学素养和解决实际 问题的重要途径。
发展的趋势
随着信息技术的发展，数学建模将更加智能化、 复杂化和实用化。
数学建模实战体验
1
选
2
从多个问题选择一个感兴趣的项目进行
研究。
3
结果报告
4
呈现研究结果和解决方案，并与其他团 队交流讨论。
组队
与同学们组队，合作解决真实问题。
模型的建立、求解、验证、优化
学习并实践数学建模的全过程，通过团 队协作完成项目。
总结
意义和应用价值
数学建模在科学研究、工程技术和决策分析等领 域具有广泛的应用和重要的价值。
特点
数学建模具有抽象性、理论性和实际可行性的特点，Байду номын сангаас一个综合运用数学、科学、技术和经 济知识的过程。
数学建模的流程和方法
1
模型的求解
2
利用数学分析和计算工具，求解数学模
型得到问题的解。
3
模型的优化
4
根据问题的要求和实际情况，对数学模 型进行改进和优化。
模型的建立
根据问题的具体情况，选择适当的数学 工具和方法，构建数学模型。
模型的验证
通过与现实数据和观察结果的比较，验 证数学模型的有效性。

《数学建模》PPT课件

《数学建模》PPT课件

( x2
x1)
f
f (x2 ) (x2 ) f
2 1 ( x1) 22
1
f
( x1 )
f
(x2 )
3
f
( x1 ) x1
f (x2 ) x2
2 (12 f (x1)f (x2 ))1/2
如函数的导数容易求得，一般首先考虑使用三次插值
法，因为它具有较高效率。对于只需要计算函数值的方
法中，二次插值法是一个很好的方法，它的收敛速度较
优化模型
（2）多项式近似法 该法用于目标函数比较复杂的情 况。此时寻找一个与它近似的函数代替目标函数，并用 近似函数的极小点作为原函数极小点的近似。常用的近 似函数为二次和三次多项式。
二次内插涉及到形如下式的二次函数数据拟合问题：
mq() a2 b c
其中步长极值为：
b
2a
完整版课件ppt
求解单变量最优化问题的方法有很多种，根据目标函 数是否需要求导，可以分为两类，即直接法和间接法。 直接法不需要对目标函数进行求导，而间接法则需要用 到目标函数的导数。
完整版课件ppt
4
优化模型
1、直接法 常用的一维直接法主要有消去法和近似法两种： （1）消去法 该法利用单峰函数具有的消去性质进行
反复迭代，逐渐消去不包含极小点的区间，缩小搜索区 间，直到搜索区间缩小到给定允许精度为止。一种典型 的消去法为黄金分割法(Golden Section Search）。黄金 分割法的基本思想是在单峰区间内适当插入两点，将区 间分为三段，然后通过比较这两点函数值的大小来确定 是删去最左段还是最右段，或同时删去左右两段保留中 间段。重复该过程使区间无限缩小。插入点的位置放在 区间的黄金分割点及其对称点上，所以该法称为黄金分 割法。该法的优点是完整算版课法件p简pt 单，效率较高，稳定性好5 。

数学建模讲座PPT课件

数学建模讲座PPT课件

决策~ 每一步(此岸到彼岸或彼岸到此岸)船上的人员 要求~在安全的前提下(两岸的随从数不比商人多),经有 限步使全体人员过河
模型构成
xk~第k次渡河前此岸的商人数 xk, yk=0,1,2,3; yk~第k次渡河前此岸的随从数 k=1,2, sk=(xk , yk)~过程的状态 S ~ 允许状态集合
航行问题建立数学模型的基本步骤
• 作出简化假设（船速、水速为常数）； • 用符号表示有关量（x, y表示船速和水速）； • 用物理定律（匀速运动的距离等于速度乘以
时间）列出数学式子（二元一次方程）； • 求解得到数学解答（x=20, y=5）；
• 回答原问题（船速每小时20公里）。
数学模型 (Mathematical Model) 和 数学建模（Mathematical Modeling)
3
法 允许状态S ~ 10个 点
允许决策D ~ 移动1或2格; 2
k奇,左下移; k偶,右上移.
d1, d11给出安全渡河方案
1 d11
s1
d1
评注和思考
0sn+1 1
2
3x
规格化方法, 易于推广 考虑4名商人各带一随从的情况
习题
• 模仿这一案例，作下面一题： 人带着猫、鸡、米过河，船除需要
人划之外，至多能载猫、鸡、米三者之 一，而当人不在场时猫要吃鸡、鸡要吃 米。试设计一安全过河方案，并使渡河 次数尽量地少。
越来越受到人们的重视。
数学建模
如虎添翼
计算机技术
知识经济
建模示例 椅子能在不平的地面上放稳吗？
问题 椅子能在不平的地面上放稳吗？
模 1.椅子四条腿一样长，椅脚与地面接触处可视为一人点，四
型 假

数学建模简单13个例子[优质ppt]

数学建模简单13个例子[优质ppt]

出，黄灯起的是警告的作用，意思是马上
要转红灯了，假如你能停住，请立即停车。
停车是需要时间的，在这段时间内，车辆
仍将向前行驶一段距离 L。这就是说，在
离街口距离为 L处存在着一条停车线（尽
管它没被画在地上），见图。对于那些黄
D
灯亮时已过线的车辆，则应当保证它们仍 能穿过马路。
L
马路的宽度D是容易测得的，问题的关键在于L的确定。
一般思维：
3 6 1 8 1 0 4 2 1 1 9 8 5 2 1 1 36 2 2222
逆向思维： 每场比赛淘汰一名失败球队，只有一名冠军，即 就是淘汰了36名球队，因此比赛进行了36场。
返回
7、气象预报问题
在气象台A的正西方向300 km处有一台风中心，它以 40 km/h的速度向东北方向移动；根据台风的强度，在距 其中心250 km以内的地方将受到影响，问多长时间后气象 台所在地区将遭受台风的影响?持续时间多长?
i1
于是，我们有了该问题的数学语言表达——数学模型
求解： 用反证法容易证明本问题的解不存在。
返回
3、相遇问题
某人平时下班总是按预定时间到达某处，然
然后他妻子开车接他回家。有一天，他比平时提早
了三十分钟到达该处，于是此人就沿着妻子来接他
的方向步行回去并在途中遇到了妻子，这一天，他
比平时提前了十分钟到家，问此人共步行了多长时
因为圆的方程为：
直线BC的方程为：
当台风中心处于圆内时，有：
其中参数t 为时间(单 位为h)。
解得
所以，大约在2h以后气象台A所在地区将会 遭受台风的影响，持续时间大约为6．6h。
8、黄灯应当亮多久
交通灯在绿灯转换成红灯时，有一个过渡状态— —亮一段时间的黄灯。请分析黄灯应当亮多久。

建模方法示例--华东理工大学数学建模课件.ppt

建模方法示例--华东理工大学数学建模课件.ppt

p1 / n1 p2 / n2 rA (n1 , n2 ) ~ 对A的相对不公平度 p2 / n2
类似地定义 rB(n1,n2)
公平分配方案应 使 rA , rB 尽量小
将一次性的席位分配转化为动态的席位分配, 即 设A, B已分别有n1, n2 席，若增加1席，问应分给A, 还是B 不妨设分配开始时 p1/n1> p2/n2 ，即对A不公平
定义 Qi
2 pi
否则, 该席给B
ni (ni 1)
, i 1,2, 该席给Q值较大的一方
2 pi
推广到m方 分配席位
2019/4/24
计算 Qi
ni (ni 1)
, i 1,2， , m
该席给Q值最大的一方 数学建模
Q 值方法
三系用Q值方法重新分配 21个席位
按人数比例的整数部分已将19席分配完毕
2019/4/24 数学建模
2.2 录像机计数器的用途
问 题
经试验，一盘标明180分钟的录像带 从头走到尾，时间用了184分，计数 器读数从0000变到6061。
在一次使用中录像带已经转过大半，计数器读数为
4450，问剩下的一段还能否录下1小时的节目？
思考
要求
2019/4/24
计数器读数是均匀增长的吗？
p1/n1– p2/n2=5 虽二者的绝对 不公平度相同
p1=1050, n1=10, p1/n1=105 p2=1000, n2=10, p2/n2=100
p1/n1– p2/n2=5 但后者对A的不公平 程度已大大降低! 数学建模
2019/4/24
“公平”分配方 法
将绝对度量改为相对度量
若 p1/n1> p2/n2 ，定义

数学建模的简单实例省名师优质课赛课获奖课件市赛课一等奖课件

数学建模的简单实例省名师优质课赛课获奖课件市赛课一等奖课件

(1)
将方桌旋转 ， 即有 2
f
(
2
)
g(0)
0
g
(
2
)
f (0) 0
于是有
h(
2
)
f
(
2
)
g(
2
)
g(0)
f
(0)
f
(0)
0
(2)
综合(1)(2)两式可见
h(
)在闭区间[0,
2
]上满足零点定理的全部
条件
于是存在 (a, b)使h( ) f ( ) g( ) 0 又由已知有f ( ) g( ) 0
xi (i 1,2,3,4,5)表示第i个槽中所装弹子的个数
A中的元素可表示为( x1 , x2 , x3 , x4 , x5 )
xi 应满足 xi1 xi 4
i 1,2,3,4
锁具问题的数学模型
A
(
x1
,
x2
,
x3
,
x4
,
x5
)
xi xi
1,2,3,4,5,6, xi1 4, i
i
求证 : 存在， 使f ( ) g( ) 0
证明： 为确定起见， 无妨设g(0) 0
1、 若f (0) 0， 取 0， 即得证。 2、 若f (0) 0, 构造函数h( ) f ( ) g( )
由f ( )和g( )的连续性知h( )是连续函数且
h(0) f (0) g(0) f (0) 0
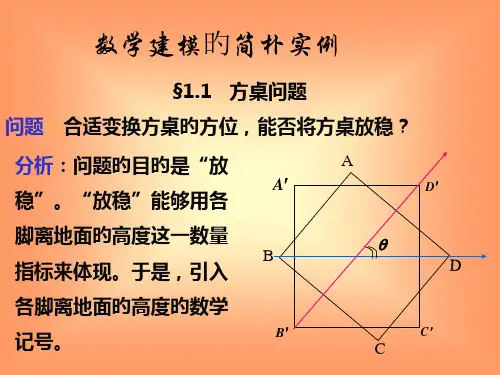
BD位置 记转过的角度为 B
则四脚离地面的高度均 可由
唯一确定。 于是这四个高度均
可视为的函数
B
若置放方桌的地面为连 续曲面,
C

数学建模 小组专题PPT-铅球投掷模型

数学建模 小组专题PPT-铅球投掷模型

• 2.2 模型假设
• 假设1：以水平面为参考系，设运动员的出 手高度为h，出手角度为θ，出手速度为 V。，铅球达到最高点时经历时间为t1，从 最高点下落到水平面的时间为t2，在总时 间T=t1+t2内铅球水平方向经过的路程即为 S。
• 假设2.铅球在空气中所受的阻力对其运动 影响甚小，忽略不计。
• 假设3.不考虑运动员推铅球时用力展臂的 动作。
g
⑤铅球水平方向经过的路程： S vx t1 t2
联立以上5个方程最后可得掷远距离S与出手速度、出手角
度、出手高度的函数关系式：
S
2hv02 cos2 (v02 sin 2 )2 v02 sin 2
g
2g
2g
（因为对出手高度没有要求，可设出手高度 h=1.8m ,g为重力加速度，取 9.8m/s^2 ）
9102 铅球掷远数学建模
小组成员：邹琪涛、林景煌、卓红滨
1 背景及问题的提出
• 铅球掷远比赛的场地是直径2.135m的圆，要求运动员从场地中将7.257kg重的铅球掷在45°的扇形区域内，如图1 。 观察运动员的比赛录像发现，他们的投掷角度变化较大，一般在38°~45°，有的高达55° ， 建立模型讨论以下问题：
2.3 模型建立
如图2为铅球斜抛运动简易图，对铅球的运动求解：
vx v0 cos ,
①将出手速度V。在水平及竖直方向分解：vy ②铅球从开始抛出到最高点经历时间： t1
v v0 y g
sin
③铅球最高点处到抛出位置的垂直高度:
t h1
1 2
g
2
1
④铅球从最高点落到水平面的时间： t2
2h h1
s(0) 0, s(0) v0 cos

数学建模优化建模实例课件

数学建模优化建模实例课件

6米钢管根数 0 1 0 2 1 3 0
8米钢管根数 0 0 1 0 1 0 2
余料(米) 3 1 3 3 1 1 3
为满足客户需要，按照哪些种合理模式，每种模式
切割多少根原料钢管，最为节省？
两种 1. 原料钢管剩余总余量最小 标准 2. 所用原料钢管总根数最少
18
决策 变量 xi ~按第i 种模式切割的原料钢管根数(i=1,2,…7) 目标1（总余量） Min Z1 3x1 x2 3x3 3x4 x5 x6 3x7
模型建立
xij--第i 种货物装入第j 个货舱的重量
目标 函数 (利润)
Max Z 3100(x11 x12 x13) 3800(x21 x22 x23) 3500(x31 x32 x33) 2850(x41 x42 x43)
货舱 x11 x21 x31 x41 10 重量 x12 x22 x32 x42 16
3
货机装运
模型建立
xij--第i 种货物装入第j 个货舱的重量
约束
平衡 要求
x11 x21 x31 x41 10
x12 x22 x32 x42 16
10； 6800
16； 8700
8； 5300
条件
x13 x23 x33 x43 8
货物 供应
x11 x12 x13 18 x21 x22 x23 15
如何装运， 使本次飞行 获利最大？
1
货机装运
模型假设
每种货物可以分割到任意小； 每种货物可以在一个或多个货舱中任意分布； 多种货物可以混装，并保证不留空隙；
模型建立
决策 xij--第i 种货物装入第j 个货舱的重量(吨） 变量 i=1,2,3,4, j=1,2,3 (分别代表前、中、后仓)

数学建模思想及案例分析PPT课件

数学建模思想及案例分析PPT课件
16
如何准备
三个人都需要 –学习－交流－再学习 –以往年论文为线索，逐篇学习交流 –不要浅谈辙止，要深入 –有问题要追根问底 –把自己当成一个科研工作者
17
如何准备
程序员 –了解Matlab的各种功能 –熟悉m文件结构 –读文章时认认真真编写每个程序 –注意提高编程效率
18
学习总结
经常不断地学习,你就什么都知道。你知道得越多,你就越有力量 Study Constantly, And You Will Know Everything. The More
到生活中去
3
什么是数学模型（二）
问题
问题
新问题
提炼归纳得 到数学结论
延伸，推导
数学方法
解决问题 解决问题
解决问题
4
怎样建立一个数学模型
数学建模所需具备的能力
细心观察 平时积累 扎实基础 高效编程 流畅文笔
在身边寻找问题，勤于思考 学习他人如何数学建模 扎实，娴熟的数学基础 高效，可靠的程序保障求解过程 条理清晰，点到为止
20
好的科技论文具备的要素
行文流畅
简明扼要
条理清晰
结构明朗
切忌拖沓
注意对象
10
什么样的模型是一个好模型（一）
正确性 简要性 创新性 稳定性
11
正确性
模型的正确性是模型存在的基础
建模的目的在于正确的解决实际问题
宁可牺牲创新性，也要保证正确性。 正确性的标准
能够较好的解决或合理的解释实际问题
本质的正确性
简要性包含两层意思：
对实际问题进行简化，是实际问题的一个近似。 抓住主要矛盾，去掉次要矛盾，抓本质
物理定律的提出是模型简要性的典范例子

数学建模实例ppt课件

数学建模实例ppt课件

B
的化学物质Z已泻入湖中，初步估计Z的量在5~20m3之间。 建立一个模型，通过它来估计湖水污染程度随时间的变化
并估计：
（1）湖水何时到达污染高峰；
（2）何时污染程度可降至安全水平(<0.05%)
28
湖泊污染问题分析
设湖水在t时的污染程度为C(t)， X
即每立方米受污染的水中含有Cm3 A
的化学物质和(1-C)m3的清洁水。用
23
几何关系
dy tg y at
dx
x
即 x dy y at dx
24
如何消去时间t?
1、求导：
2、速度与路程的关系： x 得：
（这里有负号是因为s随x的减小而增大） 4、将第2、3步代入第1步，可得模型
25
追线模型：
x
d2y dx2
k
1 dy 2 dx
由已知，T (0) 37 , T (t) 29 , T (t 1) 27 可得微分方程的特解：
T (t) 16 4 t 21 3
由T (t) 29，代入解得 t 2.4094
因此死者大约是在前一天的夜晚10:35被害的。
图1 尸体的温度
下降曲线
4
建立微分方程的常用方法
1、按变化规律直接列方程，如： 利用人们熟悉的力学、数学、物理、化学等学科中的规律，
19
（1）问题分析与模型的建立
1、放射性衰变的这种性质还可描述为“放射性物 质在任意时刻的衰变速度都与该物质现存的数量 成比例”。而C14的比例数为每年八千分之一。
2、碳14年代测定可计算出生物体的死亡时间；所
以，我们问题实际上就是：“这人死去多久了？”
若设t为死后年数，y(t)为比例数，则y(t)=C14/C12

数学建模方法ppt课件

数学建模方法ppt课件

微
了很大作用。
分
方
应用实例：
程 模
单种群模型(Malthus Logistic )
型
两种群模型
传染病模型（SI SIS SIR）
作战模型
商品销售模型
回归分析是研究变量间统计规律的方法，属于”黑 箱“建模中常用的方法，根据自变量的数值和变化， 估计和预测因变量的相应数值和变化。有线性回归和 非线性回归。
点击添加文本
)点b2击添加文本
ax1m,1x点x21 ,击添a,m加x2nx文2本0 amnxn (, )bn
点击添加文本
建模步骤：
1.建立模型：找出目标函数及相应的限定条件
2.模型的求解：可利用Lin点go击软添件加进文行本求解模型。
3.结果分析
4.灵敏度分析：改变个别相关系数观察最优解是否会
min{D( p, k), D(q, k)}
点击添加文本
点击添加文本
步骤4：重复步骤2和步骤3，直至满足聚类为止。
对于不确定性问题，又可分为随机不确定性与模 糊不确定性两类。模糊数学就是研究属于不确定性， 而又具有模糊性量的变化规律的一种数学方法。
模
点击添加文本
糊
数 学
原理关键词： 模糊集 隶属函数 模糊关系 模糊矩阵
yi 0 1xi1 2 xi2 p xip , i 1,2,, n
其中， i 是随机误差，相互独立且满足E(i ) 0, var(i ) 2
一般非线性模型的形式： 其中， f 是一般的非线性函数， 是 p维参数向量， 是一随机 误差变量，E( ) 0, var( ) 2
，把 Gp 和 Gq 合并
步骤3：计算新类与其他类的距离 点击添加文本
D(r, k) min{d (r, k) r Gr , k Gk , k r} min{d ( j, k) j Gp Gq , k Gk , k j}
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
转换成脂肪量＝1300 – 16W（cal）
3、体重的变化／天＝
W t
(千克／天) dW
t0 dt
10
1、翻译或转化： 2、配备物理单位： 3、建立表达式： 4、确定条件：
11
单位匹配
有些量是用能量(cal)的形式给出的，而另外 一些量是用重量的形式(cal)给出，考虑单位 的匹配，利用
1kg cal 10000
如牛顿第二定律，放射性物质的放射规律等。对某些实际问题 直接列出微分方程． 2、利用微元分析方法建模
根据已知的规律或定理，通过寻求微元之间的关系式得出 微分方程。 3、模拟近似法，如：
在生物、经济等学科中，许多现象所满足的规律并不很清 楚，而且现象也相当复杂，因而需根据实际资料或大量的实验 数据，提出各种假设，在一定的假设下，给出实际现象所满足 的规律，然后利用适当的数学方法得出微分方程。
12
1、翻译或转化： 2、配备物理单位： 3、建立表达式： 4、确定条件：
13
建立表达式
（1）当0 t 3 时，每天体重的变化：
dW (25001200) 16W
dt
10000
积分后可求得其通解为：
W
(t)
81.25
C e0.0016t 1
初始条件为：W0 57.1526 ，代入解出 C1 24.0974
微分方程模型
一、微分方程建模简介 二、微分方程模型 三、微分方程案例分析 四、微分方程的MATLAB求解 五、微分方程综合案例分析
1
一、微分方程模型简介
微分方程是研究变化规律的有力工具，在科 技、工程、经济管理、生态、环境、人口和 交通各个领域中有广泛的应用。 不少实际问题当我们采用微观眼光观察时都 遵循着下面的模式： 净变化率＝输入率－输出率（守恒原理）
则 W (t) 81.25 24.0974e0.0016t
W (3) 57.26799kg
14
（2）当3 t 4 时，每天体重的变化：
dW (3500 1200) 16W
dt
10000
积分后可求得其通解为：
W
(t)
143.75
C e0.0016t 2
初始条件为：W (3) 57.26799，代入解出
现回答上述问题
（1）t 6 代入对应方程，求得
W (6) 57.48247kg
（2）要满足体重不增，即dW (b 16W ) /10000 0
dt
所以b 16W 1657.1256 914 (cal)
因此每天总卡路里摄取量是1200+914＝2114cal
（3）由于每天不摄取能量，所以
dW dt
5
二、微分方程模型
微分方程的建模步骤
1、翻译或转化：
在实际问题中许多表示导数的常用词，如
“速率”、‘增长”(在生物学以及人口问题研究中)，
“衰变”(在放射性问题中)，以及“边际的”(在经
济学中)等．
2、建立瞬时表达式：根Βιβλιοθήκη 自变量有微小改变△t时，因变量的增
量△W，建立起在时段△t上的增量表达式，令
0.0016W
解得 W (t) W (0)e0.0016t 57.1526e0.0016t
因此，n周后的体重为W (7n) 57.1526e0.0011687n
案例2 在一个巴基斯坦洞穴里，发现了具有古代 尼安德特人特征的人骨碎片，科学家们把它们带 到实验室，作碳14年代测定。分析表明C14与C12的 比例仅仅是活组织内的6.24％，此人生活在多少年 前？
由已知，T (0) 37 , T (t) 29 , T (t 1) 27 可得微分方程的特解：
T (t) 16 4 t 21 3
由T (t) 29，代入解得 t 2.4094
因此死者大约是在前一天的夜晚10:35被害的。
图1 尸体的温度
下降曲线
4
建立微分方程的常用方法
1、按变化规律直接列方程，如： 利用人们熟悉的力学、数学、物理、化学等学科中的规律，
案例1：一位女士每天摄入2500cal食物，1200cal 用于基本新陈代谢(即自动消耗)，并以每千克体重 消耗16cal用于日常锻炼，其他的热量转变为身体 的脂肪（设10000cal可转换成1kg脂肪）。星期天 晚上，该女士的体重是57.1526kg，星期四那天她 饱餐了一顿，共摄入了3500cal的食物，要求建立 一个通过时间预测体重的数学模型，并用它估计： （1）星期六该女士的体重？ （2）为了不增重，每天她最多的摄入量是多少？ （3）若不进食，N周后她的体重是多少？
C2 86.89812
则 W (t) 81.25 86.89812e0.0016t
W (4) 57.40625kg
15
（2）当t 4 时，食物的摄入量恢复正常
dW (2500 1200) 16W
dt
10000
积分后可求得其通解为：
W
(t
)
81.25
C e0.0016t 3
初始条件为：W (4) 57.40625，代入解出
C3 23.9968
则 W (t) 81.25 23.9968e0.0016t
16
最后得到不同阶段的微分方程是：
81.25 24.0974e0.0016t ,
W
(t
)
143.75
86.8981e0.0016t
,
81.25 23.9968e0.0016t ,
0t 3 3t 4 t4
17
2
引例一
在凌晨1时警察发现一具尸体，测得尸体温度是 29oC，当时环境的温度是21oC。1h后尸体温度下 降到27oC，若人体的正常温度是37oC，估计死者 的死亡时间。
解：设T(t)为死者在被杀害后t时刻尸体的温度；k 为比例系数。由牛顿冷却定律，得
则通解为
dT dt k(T T0 )
T Cekt 21 3
△t →0，即得到 dW 的表达式．
dt
6
3、配备物理单位： 在建模中应注意每一项采用同样的物理单位．
4、确定条件： 这些条件是关于系统在某一特定时刻或边界
上的信息，它们独立于微分方程而成立，用以确 定有关的常数。为了完整充分地给出问题的数学 陈述，应将这些给定的条件和微分方程一起列出。
7
二、微分方程案例分析
8
解
1、翻译或转化： 2、配备物理单位： 3、建立表达式： 4、确定条件：
9
1、“每天”：体重的变化＝输入一输出 其中输入指扣除了基本新陈代谢之后的净重量 吸收；输出是进行健身训练时的消耗．
2、上述陈述更好的表示结构式： 取天为计时单位，记W(t)为t天时体重(kg)，则： 每天的净吸收量＝2500 – 1200 ＝1300（cal) 每天的净输出量＝16(cal)×W＝16W(cal)