下载文档原格式
104 高斯色噪声中信号检测的思路（1）色噪声：噪声的功率谱密度在整个频带内的分布是非均匀的。
色噪声的自相关函数不再是δ函数，故色噪声在任意两个不同时刻的取值不再是不相关的。
（2）高斯色噪声：服从高斯分布的色噪声。
（3）高斯色噪声中信号检测的基本方法：一种是白化处理方法，另一种是卡亨南-洛维（Karhunen-Loeve ）展开方法。
（4）白化处理方法：先将含有高斯色噪声的接收信号通过一个白化滤波器，使输入白化滤波器的色噪声在输出端变为白噪声，然后再按白噪声中信号检测的方法进行处理。
（5）卡亨南-洛维展开方法：把含有高斯色噪声的信号表示成正交展开的形式，将正交展开的系数作为样本，从而使样本是相互统计独立的。
通过求取卡亨南-洛维展开系数的概率密度，并将它们相乘，得到所有卡亨南-洛维展开系数的联合概率密度（即含有高斯色噪声的信号的多维概率密度）；再由卡亨南-洛维展开系数的联合概率密度得到不同假设下的似然函数，从而就可以进行似然比检测。
2 卡亨南-洛维展开1．随机信号的正交展开（1）正交函数集在时间),0(T 上定义的函数集},2,1),({ =k t f k ，如果满足⎰⎩⎨⎧≠==*Ti k ik ik t t f t f 001d )()( （5.2.1） 则称此函数集是正交函数集。
（2）完备的正交函数集如果在平方可积或能量有限的函数空间中，不存在另一个函数)(t g ，使⎰==*Tk k t t g t f 0,2,10d )()( （5.2.2）则正交函数集},2,1),({ =k t f k 称为完备的正交函数集。
（3）随机信号的正交展开在时间),0(T 上的任意平方可积随机信号)(t x 的正交展开表示为∑∑∞==∞→==11)()(lim)(k k k mk k km t f x t f xt x （5.2.3）其展开系数k x 为⎰==*Tk k k t t f t x x 0,2,1d )()( （5.2.4）105对于随机信号)(t x ，展开系数k x 是随机变量，因此随机信号)(t x 的正交展开应在平均意义上满足0)()(lim 21=⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧⎥⎦⎤⎢⎣⎡-∑=∞→m k k k m t f x t x E （5.2.5） 即正交展开的均方误差等于零，或者说正交展开均方收敛于)(t x 。
作业11．什么是白噪声？白噪声有何特点？答：白噪声是均值为0，自相关函数为冲击响应的随机过程。
白噪声的功率谱为常数。
2. 一个离散时间的随机信号由两个正弦波信号叠加而成，即()x t =1sin()A t ω+ 2cos()B t ω，i ω=2i f π，i =1，2，其中幅值A 和B 为独立的高斯随机变量，具有以下概率密度221/(2)()a A f a σ-=，222/(2)()b B f a σ-= 求离散时间信号()x t 为严格平稳随机信号的条件。
解：由于()x t 为两个正弦信号的线性叠加，因此()x t 也是正弦信号。
又因为{()}E x t =1{sin()}E A t ω+ 2{cos()}E B t ω=0{()}D x t =1{sin()}D A t ω+ 2{cos()}D B t ω=2211sin ()t σω+2222cos ()t σω 所以，()x t 的概率密度函数可以表示为222221122/2[sin ()cos ()](,)x t t f x t σωσω-+=若1σ=2σ=σ，1ω=2ω，则{()}D x t =2σ此时的()x t 的概率密度函数可以表示为22/2(,)x f x t σ-=因此(,)f x t 将与t 无关，因此()x t 为严格平稳的条件为1σ=2σ，1ω=2ω作业21. 在一个3发射4接收的MIMO 无线通信系统中，系统在白噪声的环境下采用训练序列估计信道00h ，10h 和20h ，其中ij h 表示用户i 的数据发射到天线j 时经过的单径信道，训练序列的块长为16，请用最小二乘估计方法估计这三个信道。
解：信道0H =[00h , 10h , 20h ]T ,第0个用户的发射数据为0X =[0,0x , 0,1x , …0,15x ]T 第1个用户的发射数据为1X =[1,0x , 1,1x , …1,15x ]T 第2个用户的发射数据为2X =[2,0x , 2,1x , …2,15x ]T 则我们在第0个天线处接收到的数据为 0Y =0XH +N其中X =[0X , 1X , 2X ], N 为白噪声向量 因此最后的0H 的最小二乘估计表达式为 0ˆH =0+X Y作业31．若一条件概率密度函数为高斯分布，则采用该分布函数所获得的绝对损失型、二次型和均匀型Bayes 估计的结果之间有何关系？为什么？ 答：估计结果相等。
32 4.1 内容提要及结构本章首先介绍高斯白噪声统计特性及随机信号的采样定理，然后依次讨论高斯白噪声中二元确知信号检测、多元确知信号检测、二元随机参量信号检测以及多重二元信号的检测。
本章内容实际是将信号检测的基本理论具体应用到高斯白噪声信号检测的情况，并且主要讨论的是理想高斯白噪声中信号检测方法及性能分析方法；本章主要讨论一般的似然比检测方法，而不指定哪一个具体准则。
本章内容逻辑结构如图4.1.1所示。
4.2 目的及要求本章的目的是使学习者从概率分布、相关函数和功率谱密度等方面理解高斯白噪声的特点，熟悉随机信号的采样定理；掌握带限高斯白噪声和理想高斯白噪声中二元确知信号检测方法，尤其掌握理想高斯白噪声中观测信号的似然函数，掌握理想高斯白噪声中二元确知信号检测性能分析方法；掌握理想高斯白噪声中多元确知信号检测方法及性能分析方法；掌握理想高斯白噪声中二元随机参量信号检测方法及性能分析方法；理解和熟悉高斯白噪声中多重二元信号检测的概念及使用条件，掌握高斯白噪声中多重二元确知信号和二元随机参量信号检测方法及性能分析方法。
4.3 学习要点4.3.1 高斯白噪声● 内容提要：本小节从高斯噪声和白噪声两个方面论述高斯白噪声的概念，从概率分布、相关函数和功率谱密度等方面论述高斯白噪声的统计特性，简要讨论低通和带通随机信号采样定理。
● 关键点：从高斯噪声和白噪声两个方面理解高斯白噪声的概念，从概率分布、相关函数和功率谱密度等方面掌握高斯白噪声的统计特性，熟悉低通和带通随机信号采样定理。
1．噪声噪声是指与接收的有用信号混杂在一起而引起信号失真的不希望的信号，是一种随机信号或随机过程。
2．高斯白噪声 高斯白噪声是一种幅度分布服从高斯分布，功率谱密度在整个频带内为常数的随机信号或随机过程。
高斯白噪声既具有高斯噪声的特性，又具有白噪声的特性。
确知信号的检测二元确知信号 的检测 多元确知信号 的检测带限高斯白噪声中二元确知信号的检测理想高斯白噪声中二元 确知信号的检测二元随机振幅和相位信号的检测二元随机相位信号的检测3．高斯噪声1）高斯噪声定义高斯噪声是一种幅度分布服从高斯分布的随机信号或随机过程。
1、数字通信的特点有哪些？答：数字通信具有以下几个主要特点。
（1）抗干扰能力强，无噪声积累（2）便于加密处理（3）采用时分复用实现多路通信 （4）设备便于集成化、微型化（5）占用信道频带较宽1、为什么要进行调制？调制的主要功能有哪些？ 答：采用高频载波调制传输的主要原因有两个：（1）在无线通信中由于要传输的信息基本上都属于低频范围，如果将此低频信号直接发射出去，需要的发射和接收天线尺寸太大，辐射效率太低，不易实现。
我们知道，天线如果要想有效辐射，需要天线的尺寸l 与信号的波长λ可以比拟。
即使天线的尺寸为波长的十分之一，即10/λ=l ，对于频率为1kHz 的信号，需要的天线长度为30km ，这样长的天线几乎是无法实现的。
若将信号调制到10MHz 的载波频率上，需要的天线长度仅为3m ，这样的天线尺寸小，实现起来也比较容易。
（2）在有线信道通信中可以实现频分多路复用。
主要功能：（1）将消息变换为便于传输的形式（适应信道传输）。
（2）提高性能，提高抗干扰性。
（3）有效的利用频带（合并多路信号）。
（4）容易辐射。
（5）调制把基带信号频谱搬移到一定的频带范围以适应信道的要求。
4、从下面的眼图模型可以说明哪些问题？（10分） 答：从上眼图说明以下几个问题：（1）最佳抽样时刻应在“眼睛”张开最大的时刻；（2）对定时误差的灵敏度由眼图的斜边之斜率确定，斜率越大，对定时误差越灵敏； （3）阴影区的垂直高度表示信号畸变范围； （4）图中央横轴位置应对应判决门限电平；（5）在抽样时刻上，上下两阴影区的间隔距离之半为噪声容限。
3、已知一基带信号t t t m ππ4cos 22cos )(+=，对其进行理想抽样：（1） 为了在接收端能不失真地从已抽样信号)(t m s 中恢复)(t m ，试问抽样间隔应如何选择？（2） 若抽样间隔取为，试画出已抽样信号的频谱图。
解：（1）基带信号可看成低通信号，其最高频率Hz f m 2=，所以抽样速率f 11（24、12路载波电话信号占有频率范围为60-108kHz，求出其最低抽样频率?min=sf并画出理想抽样后的信号频谱。
一、概念:1. 匹配滤波器。
概念：所谓匹配滤波器是指输出判决时刻信噪比最大的最佳线性滤波器。
应用:在数字信号检测和雷达信号的检测中具有特别重要的意义。
在输出信噪比最大准则下设计一个线性滤波器是具有实际意义的。
2. 卡尔曼滤波工作原理及其基本公式(百度百科)首先,我们先要引入一个离散控制过程的系统。
该系统可用一个线性随机微分方程（Linear StoｃhastiｃDifferｅｎce equatiｏn）来描述：X(k）=A X(k－1)+BＵ(k)+W(ｋ)再加上系统的测量值:Z(k)＝ＨＸ(k)+V(k)上两式子中，Ｘ(k)是k时刻的系统状态,U(k）是k时刻对系统的控制量。
A和B是系统参数，对于多模型系统,他们为矩阵。
Z(k)是k时刻的测量值,H是测量系统的参数，对于多测量系统,H为矩阵。
Ｗ(k)和V（k)分别表示过程和测量的噪声。
他们被假设成高斯白噪声(Whｉte ＧausｓｉaｎNoiｓe），他们的coｖaｒiancｅ分别是Q，R（这里我们假设他们不随系统状态变化而变化）。
对于满足上面的条件(线性随机微分系统,过程和测量都是高斯白噪声),卡尔曼滤波器是最优的信息处理器。
下面我们来用他们结合他们的covariａncｅs来估算系统的最优化输出（类似上一节那个温度的例子）。
首先我们要利用系统的过程模型，来预测下一状态的系统。
假设现在的系统状态是k,根据系统的模型,可以基于系统的上一状态而预测出现在状态：Ｘ(k|ｋ－1）=A X(k-１|k－1）+B U(k) ……….．(1)式(１)中，X（k|k-1)是利用上一状态预测的结果，X（k-１|k－１)是上一状态最优的结果,Ｕ(k)为现在状态的控制量，如果没有控制量,它可以为0。
到现在为止，我们的系统结果已经更新了,可是,对应于X(ｋ｜k-1)的covａｒiancｅ还没更新。
我们用P表示covａｒianｃe:P(k|ｋ-１)=A P(k-1｜ｋ－１)Ａ’+Q (2)式(2)中,P（k｜ｋ－1）是X（k|k-1)对应的covaｒｉaｎce,P(ｋ-１|k-1）是Ｘ(k-1|k-1)对应的cｏvariaｎce,A’表示A的转置矩阵,Q是系统过程的cｏvａriance。
第三章1、 设在某二元通信系统中，有通信信号和无通信信号的先验概率分别为：P(H 1)=0.8，P(H 0)=0.2。
若对某观测值x 有条件概率分布f(x|H 1)=0.25和f(x|H 0)=0.45，试用最大后验概率准则对该观测样本x 进行分类。
2、在存在加性噪声的情况下，测量只能为2v 或0v 的直流电压，设噪声服从均值为0、方差为 2σ的正态分布，设似然比门限值为0l ，试对测量结果进行分类（10分）3、设二元假设检验的观测信号模型为：H0:x=-1+nH1:x=1+n其中n 是均值为零、方差为1/2的高斯观测噪声。
若两种检验都是等先验概率的，而代价因子为： C 00=1 ,C 10=4, C 11=2 C 01=8。
试求Bayes 判决表示式，并画出bayes 接收机形式。
4、设x1,x2,…xn 是统计独立的方差为2σ的高斯随机变量，在H1假设下均值为a1，H0假设下均值为a0，似然比门限为0l ，试对其进行判决，并求两种错误概率。
（20分）5、在二元数字通信系统中，时间间隔T 秒内，发送一个幅度为d 的脉冲信号，即s 1=d,代表1；或者不发送信号，即s 0=0，代表0。
加性噪声服从均值为0，方差为1的高斯分布，当先验概率未知，正确判决不花代价，错误判决的代价相等且等于1时，采用极大极小准则计算其极大极小风险为多大，相应的q 0为多少？6、在加性噪声背景下，测量0V 和1v 的直流电压在P(D1|H0)=0.1的条件下，采用Neyman-Pearson 准则，对一次测量数据进行判决。
假定加性噪声服从均值为0，方差为2的正态分布。
（已知erf(0.9)=0.7969）第四章 1、已知发送端发送的信号分别为⎩⎨⎧≤≤-=≤≤=T t t A t s T t t A t 0,sin )(0,sin )(s 10ωω 试利用最小错误概率准则设计一台接收机，对如下假设做出判决，并画出接收机的结构形式。
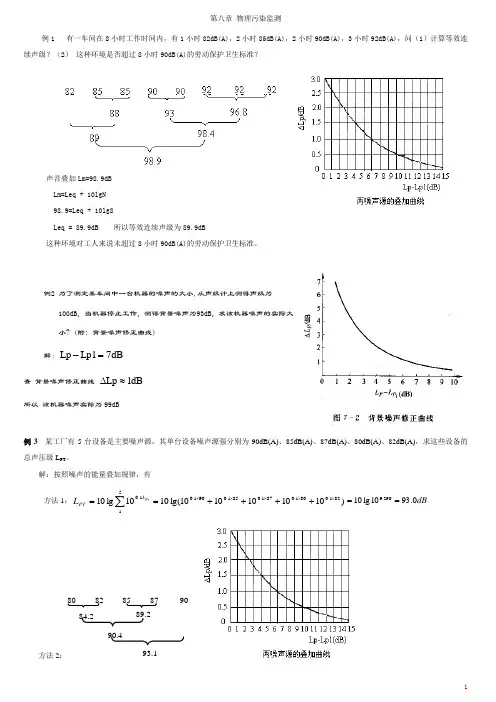
例1 有一车间在8小时工作时间内，有1小时82dB(A)，2小时85dB(A)，2小时90dB(A)，3小时92dB(A)，问（1）计算等效连续声级？（2） 这种环境是否超过8小时90dB(A)的劳动保护卫生标准？声音叠加Lm=98.9dBLm=Leq + 10lgN98.9=Leq + 10lg8Leq = 89.9dB 所以等效连续声级为89.9dB这种环境对工人来说未超过8小时90dB(A)的劳动保护卫生标准。
例2 为了测定某车间中一台机器的噪声的大小,从声级计上测得声级为100dB ，当机器停止工作，测得背景噪声为93dB ，求该机器噪声的实际大小? (附: 背景噪声修正曲线)解：dB 7Lp1Lp =-查 背景噪声修正曲线 dB 1Lp ≈∆所以 该机器噪声实际为99dB例3 某工厂有5台设备是主要噪声源，其单台设备噪声源强分别为90dB(A)、85dB(A)、87dB(A)、80dB(A)、82dB(A)，求这些设备的总声压级L PT 。
解：按照噪声的能量叠加规律，有方法1：)1010101010lg(1010lg 10821.0801.0871.0851.0901.0511.0⨯⨯⨯⨯⨯++++==∑P i L PT L dB 0.9310lg 10296.9==方法2：80 82 85 87 9084.289.290.493.1一、填空题1 计权声级有四种类型，即A、B、C、D，在噪声监测中使用较多的，模似人耳对55dB以下低强度噪声的滤波原理设计的是_____计权声级2 Leq、L10、L50和L90的含义分别为____________________,_________________________,____________________,____________________.3 声音传播的三要素是_____________、____________和_____________。
XXX 大学（学院）试卷《信号检测与估计》试卷 第 1 页 共 2 页 《信号检测与估计》模拟试卷一、填空题（每空1分，共10分）1．广义匹配滤波器可通过 和 级联而构成。
2．卡亨南-洛维展开是把平稳随机信号表示成 的形式，并使 。
3．修正的奈曼-皮尔逊准则是在给定 和 的条件下，从第一个观测数据开始就进行似然比检测，直至能做出判决为止。
4．秩检测是一种利用观测样本的 和 的一种非参量检测方法。
5．最小二乘估计的使用条件：含有被估计参量的信号模型已知， 和 的任何统计知识均未知。
二、简答题（每题4分，共20分）1．概述高斯白噪声情况下和高斯色噪声情况下信号检测所采用方法的特点。
2．简述序列检测的概念与特点。
3．简述非参量检测的概念、特点及基本原理。
4．简要说明在似然函数对的频率偏导数难以求解情况下，信号频率估计的方法。
5．说明参量的最小二乘估计方法的基本思路。
三、（10分）设线性滤波器的输入为)()()(t n t s t x +=，其中)(t n 是功率谱密度为2/0N 的白噪声，信号为⎩⎨⎧><≤<-=T t t T t t T A t s ,000)()( 式中，0>A ，且为常数。
（1）试求匹配滤波器的冲激响应及对应于)(t s 的输出信号。
（2）求匹配滤波器输出的信噪比。
四、（10分）对于二元随机参量信号的检测问题，若两个假设下观测信号分别为：n x H =:0，n s x H +=:1，其中，信号s 和噪声n 是相互统计独立的随机变量，其概率密度函数分别为⎩⎨⎧<>≥-=0,00,0,)exp()(s a s s a a s p ⎩⎨⎧<>>≥-=0,00,0,)exp()(n a b b n n b b n p 且 设似然比检验门限为0Λ，试证明信号的似然比检测判决式可化简为γ10H H x<>。
五、（15分）在T t ≤≤0时间范围内，二元通信系统发送的二元信号为t A t s 00sin )(ω=，。
通信原理大作业1、说明在通信原理课程中，介绍了通信系统的基本理论，主要包括信道、基带传输、调制/ 解调方法等。
为了进一步提高和改善学生对课程基本内容的掌握，进行课程作业方法的改革的试点，设立计算机仿真大作业。
成绩将计入平时成绩。
2、要求参加的同学3~5人一组，选择1〜2个题目，协作和共同完成计算机编程和仿真，写出计算机仿真报告。
推荐的计算机仿真环境为MATLAB也可以选择其它环境。
3、大作业选题(1) 信道噪声特性仿真产生信道高斯白噪声，设计信道带通滤波器对高斯白噪声进行滤波，得到窄带高斯噪声。
对信道带通滤波器的输入输出的噪声的时域、频域特性进行统计和分析，画出其时域和频域的图形。
(2) 基带传输特性仿真利用理想低通滤波器作为信道，产生基带信号，仿真验证奈氏第一准则的给出的关系。
改变低通滤波器的特性，再次进行仿真，验证存在码间干扰时的基带系统输出，画出眼图进行观察。
加入信道噪声后再观察眼图。
(3) 2ASK言号传输仿真按照2ASK产生模型和解调模型分别产生2ASK言号和高斯白噪声，经过信道传输后进行解调。
对调制解调过程中的波形进行时域和频域观察，并且对解调结果进行误码率测量。
2ASK信号的解调可以选用包络解调或者相干解调法。
(4) 2FSK信号传输仿真按照2FSK产生模型和解调模型分别产生2FSK信号和高斯白噪声，经过信道传输后进行解调。
对调制解调过程中的波形进行时域和频域观察，并且对解调结果进行误码率测量。
2FSK信号的解调可以选用包络解调或者相干解调法。
(5) 2PSK信号传输仿真按照2PSK产生模型和解调模型分别产生2PSK言号和高斯白噪声，经过信道传输后进行解调。
对调制解调过程中的波形进行时域和频域观察，并且对解调结果进行误码率测量。
2PSK信号的解调选用相干解调法。
⑹2DPSK言号传输仿真按照2DPSK产生模型和解调模型分别产生2DPSK言号和高斯白噪声，经过信道传输后进行解调。
对调制解调过程中的波形进行时域和频域观察，并且对解调结果进行误码率测量。
