圆柱螺旋拉伸弹簧的设计计算

圆柱螺旋压缩（拉伸）弹簧的设计计算
一、圆柱螺旋压缩（拉伸）弹簧的设计原理
1、圆柱螺旋压缩（拉伸）弹簧原理
圆柱螺旋压缩（拉伸）弹簧是一种特殊的弹簧，其结构设计使用了螺
旋结构，螺旋结构的形状是一个圆柱形的圆柱螺纹。

圆柱螺旋压缩（拉伸）弹簧的压缩（拉伸）受力分布差异，当进行压缩（拉伸）力作用时，弹簧
的整个螺旋节在不同的力矩作用下会产生相应的弹性变形，从而使得弹簧
的中心轴变长，以缩短弹簧的长度。

2、圆柱螺旋压缩（拉伸）弹簧特性
圆柱螺旋压缩（拉伸）弹簧具有对同直径和外径的小变化具有很强的
适应性的特性，同时，压缩（拉伸）力也有必要时可以根据弹性变形率来
改变。

圆柱螺旋压缩（拉伸）弹簧的压缩（拉伸）受力分布差异，当进行
压缩（拉伸）力作用时，弹簧的整个螺旋节在不同的力矩作用下会产生相
应的弹性变形，从而使得弹簧的中心轴变长，从而缩短弹簧的长度。

此外，这种弹簧具有紧凑结构，能够有效地减少设备装置内的多余空间，重量轻，由于采用细小的钢、不锈钢、铜或其它有良好装配性的金属等材料，具有
良好的耐磨性、耐腐蚀性和耐臭氧性等性能。

圆柱螺旋拉伸弹簧的设计计算
一、定义
1、圆柱螺旋弹簧：圆柱螺旋弹簧由弯曲的螺旋条组成，可在垂直和
轴向两个轴上拉伸。

它可以提供可靠的形变响应，并具有很强的耐用性和
重复性。

2、设计计算：圆柱螺旋弹簧的设计计算主要是根据弹簧性能要求，
确定标准尺寸、曲率半径等参数，并且确定合适的材料，使弹簧工作正常。

二、材料选择
圆柱螺旋弹簧主要由碳钢和不锈钢制成，所以在选择材料时要注意材
料的弹性模量，刚度和耐腐蚀性的特点。

1、碳钢：碳钢具有良好的抗张性能，耐腐蚀性不强。

碳钢的弹性模
量比不锈钢低好多，所以轻微的弹簧最好采用碳钢。

2、不锈钢：不锈钢具有很高的弹性模量和较高的耐蚀性，因此适用
于强度较大的圆柱螺旋弹簧。

三、尺寸设计
1、外径：根据弹簧的外形和尺寸，圆柱螺旋弹簧的外径可以在固定
的范围内变化，一般为30mm-100mm。

2、螺距：一般采用固定螺距，使用相同的螺距可以达到更好的组装
精度，以减少工程成本。

3、曲率半径：曲率半径取决于弹簧的用途，一般的圆柱螺旋弹簧使
用的曲率半径为30mm-1000mm。

4、钢丝直径：根据弹簧的负载性能，确定材料和钢丝直径，以满足弹簧的负载要求。

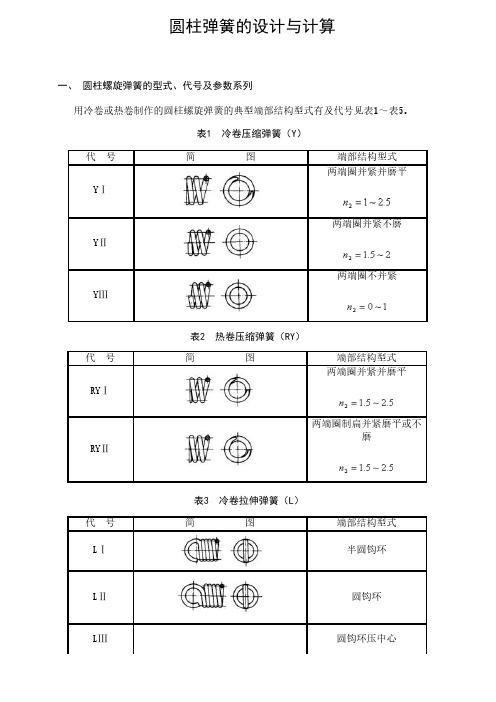
圆柱螺旋压缩弹簧计算
公式
-CAL-FENGHAI.-(YICAI)-Company One1
普通圆柱螺旋压缩及拉伸弹簧的结构尺寸（mm）计算公式
参数名称及代号计算公式备注
压缩弹簧拉伸弹簧
中径D2 D2=Cd 按普通圆柱螺旋弹簧尺寸系列表取标准值
内径D1 D1=D2-d
外径D D=D2+d
旋绕比C C=D2/d压缩弹簧长细比b b=H0/D2 b在1～的范围内选取自由高度或长度H0 H0≈pn+～2)d（两端并紧，磨平）H0≈pn+(3～d（两端并紧，不磨平） H0=nd+钩环轴向长度工作高度或长度H1,H2,…,Hn Hn=H0-λn Hn= H0+λn λn--工作变形量有效圈数n 根据要求变形量按式（16-11）计算n≥2总圈数n1 n1=n+(2～（冷卷）n1=n+～2) （YII型热卷） n1=n 拉伸弹簧n1尾数为1/4,1/2,3/4整圈。

推荐用1/2圈节距p p=～D2 p=d 轴向间距δ δ=p
-d 展开长度L L=πD2n1/cosα L≈πD2n+钩环展开长度螺旋角α α=arctg(p/πD 2) 对压缩螺旋弹簧，推荐α=5°～9°质量ms ms= γ为材料的密度，对各种钢，γ=7700kg/ ；对铍青铜，γ=8100kg/。

1. 弹簧刚度：
2. 力值： 其中：G 为材料剪切模量，一般不锈钢取71500Mpa,碳钢取
78500Mpa ；
d 为材料直径；
D 为弹簧中径；
n 为弹簧有效圈数；
f 为变形量（拉压行程）。

3. 应力： K 为曲度系数，公式为： 其中C 为弹簧旋绕比，是弹簧中径与线径的比值，即
4. 下表是GB/T23935-2009（圆柱螺旋弹簧设计计算）中压缩弹簧及拉伸弹簧的试验切应力及许用应力表
表2-1
n D d G 34
,
8P =f 8f 34,
⋅==n D Gd P P K PC K ⋅=⋅=2
3d 8d 8PD ππτC
C C K 615.04414+--=d D
C =
比压簧多了初拉力，加上初拉力就行。

初拉力： 其中初拉力τ0按初切应力图选取，见下图。

三．扭簧：
1.计算刚度 Dn
Ed M 3670'4= Nmm/° 2.扭矩 ϕ⋅=Dn
Ed M 36704
Nmm 式中:d---材料直径；
E---材料的弹性模量，一般不锈钢丝取188000Mpa ，碳素钢丝
取206000Mpa ；
D---弹簧外径；
ϕ---弹簧的扭转行程（角度）；
4. 应力： K1为曲度系数，顺旋向扭转取1，逆旋向扭转时按下式：
308τπ⋅=D d P 132
.10K d
M ⋅=σ
下表是GB/T23935-2009（圆柱螺旋弹簧设计计算）中扭转弹簧的试验切应力及许用应力表
C
C C C K 4414221---=。

弹簧参数、尺寸及计算公式弹簧参数及尺寸一、小型圆柱螺旋拉伸弹簧尺寸及参数1、弹簧的工作图及形式1.1 工作图样的绘制按GB4459、4规定。

1.2 弹簧的形式分为A型和B型两种。

2、材料弹簧材料直径为0.16~0.45mm，并规定使用GB4357中B组钢丝或YB(T)11中B组钢丝。

采用YB(T)11中B组钢丝时，需在标记中注明代号“S”。

3、制造精度弹簧的刚度、外径、自由长度按GB1973规定的3级精度制造。

如需按2级精度制造时，加注符号“2”，但钩环开口尺寸均按3级精度制造。

4、旋向弹簧的旋向规定为右旋。

如需左旋应在标记中注明“左”。

5、钩环开口弹簧钩环开口宽度a为0.25D~0.35D。

注：D为弹簧中径。

6、表面处理6.1采用碳素弹簧钢丝制造的弹簧，表面一般进行氧化处理，但也可进行镀锌、镀镉、磷化等金属镀层及化学处理。

其标记方法应按GB1238的规定。

6.2采用弹簧用不锈钢丝制造的弹簧，必要时可对表面进行清洗处理，不加任何标记。

7、标记7.1标记的组成弹簧的标记由名称、型式、尺寸、标准编号、材料代号(材料为弹簧用不锈钢丝时)以及表面处理组成。

规定如下：7.2标记示例例1:A型弹簧，材料直径0.20mm，弹簧中径3.20mm，自由长度8.80mm，左旋，刚度、外径和自由长度的精度为2级，材料为碳素弹簧钢丝B组，表面镀锌处理。

标记:拉簧A0.20*3.20*8.80-2左GB1973.2——89-D-Zn例2：B型弹簧，材料直径0.40mm，弹簧中径5.00mm，自由长度17.50mm，右旋，刚度、外径和自由长度的精度为3级，材料为弹簧用不锈钢丝B组。

标记：拉簧B0.40*5.00*17.50 GB1973.2--89-S8、计算依据标准中的计算采用如下基本公式：切应力(N/mm²)：τ=(8PDK)/(πd³)变形量(mm)：F=(8PD³n)/ Gd4弹簧钢度(N/mm):P′=P/ F=(Gd4)/(8D³n)曲度系数：K =(4C-1)/(4C-4)+ (0.615)/C旋转比：C =D/d 自由长度(mm)：H。

圆柱螺旋弹簧设计计算表
4 - 16
外径Demax. 350 mm工作线圈数nmin. 3比
率b/h1:5 - 5:1自由长度L0max. 1500 mm长细
比L0/D1 - 15间距p(0.2 - 0.4) D - 无预压弹簧
弹簧收尾设计
.
A =半圈
B = 整圈
C = 侧面整圈
D =双扭曲整圈
E = 侧面双扭曲整圈
F = 内部整圈
G =. 提高的挂勾H = 侧面提高的挂勾L = 锥形旋转小圈收尾I = 小圈J = 侧面小圈K = 倾斜的整圈
M = 锥形旋转螺栓收尾N = 螺丝状收尾O = 螺丝状束缚收尾
拉伸弹簧通常使用几种不同高度和特性的挂钩来固定（A..J）。

从技术角度讲，固定挂钩是最好的解决方案，但是，这也带来弹簧负载的一些确定问题。

弹簧负载带给挂钩集中的负载应力，该负载应力可能明显地高于弹簧线圈所计算的应力。

针对在挂钩中产生的弯曲应力，小圈（类别 I, J）或双圈（类别 D, E）是最佳方案。

针对由线变成线圈所产生的集中的扭转应力，侧边整圈（类别 C,E,I）是最佳方案。

对于挂钩的独立设计，以下挂钩高度值指定如下：
热成型弹簧，方形线圈弹簧以及循环负载弹簧通常无弹簧卡钩使用(M..O. design)。

无固定挂钩弹簧使用边缘线圈固定，弹簧功能变形中线圈间距不会变化。

圆柱螺旋拉伸弹簧的设计计算
首先，弹簧材料的选择是设计弹簧的第一步。

弹簧一般由钢材制成，
常用的有普通碳素钢、合金钢等。

材料的选择主要考虑弹性模量、屈服强
度和抗疲劳性能等指标。

一般情况下，选择具有较高屈服强度和良好抗疲
劳性能的钢材作为弹簧材料。

接下来，需要确定弹簧的几何参数，包括弹簧线圈数、线径、外径和
自由长度等。

这些参数的确定需要根据弹簧设计的工作条件和性能要求进
行计算。

其中，弹簧线圈数的确定是根据弹簧的刚度要求和可用的安装空
间来确定的。

线径和外径的选择需要考虑到弹簧的受力情况，一般来说，
线径越大，弹簧的刚度越大，外径越大，弹簧的承载能力越大。

自由长度
是指弹簧在没有受力时的长度，它的选择需要考虑到装配和安装上的要求。

最后，弹簧的刚度需要根据设计要求来确定。

弹簧的刚度表示了弹簧
在受力时的变形程度，刚度越大，变形越小。

弹簧的刚度可以通过加载和
测量弹簧受力变形来确定，也可以通过计算公式进行估算。

常用的计算公
式有虎克公式、彼得逊公式和牛顿公式等。

根据这些公式，可以根据弹簧
的几何参数和受力情况来计算弹簧的刚度。

总结起来，圆柱螺旋拉伸弹簧的设计计算包括弹簧材料的选择、弹簧
的几何参数计算以及刚度的确定等。

在进行计算时，需要考虑到弹簧设计
的工作条件和性能要求，并通过加载和测量弹簧受力变形或计算公式来确
定弹簧的各项参数。

这样设计出的弹簧可以满足工程应用的需求，保证安
全可靠地工作。

圆柱螺旋压缩（拉伸）弹簧的设计计算(一)几何参数计算普通圆柱螺旋弹簧的主要几何尺寸有：外径D、中径D2、内径D1、节距p、螺旋升角α及弹簧丝直径d。

由下图圆柱螺旋弹簧的几何尺寸参数图可知，它们的关系为：式中弹簧的螺旋升角α，对圆柱螺旋压缩弹簧一般应在5°～9°范围内选取。

弹簧的旋向可以是右旋或左旋，但无特殊要求时，一般都用右旋。

圆柱螺旋弹簧的几何尺寸参数普通圆柱螺旋压缩及拉伸弹簧的结构尺寸计算公式见表([color=#0000ff 普通圆柱螺旋压缩及拉伸弹簧的结构尺寸（mm）计算公式)。

普通圆柱螺旋压缩及拉伸弹簧的结构尺寸（mm）计算公式质量m sm s=γ为材料的密度，对各种钢，γ=7700kg/；对铍青•(二)特性曲线弹簧应具有经久不变的弹性，且不允许产生永久变形。

因此在设计弹簧时，务必使其工作应力在弹性极限范围内。

在这个范围内工作的压缩弹簧，当承受轴向载荷P时，弹簧将产生相应的弹性变形，如右图a所示。

为了表示弹簧的载荷与变形的关系，取纵坐标表示弹簧承受的载荷，横坐标表示弹簧的变形，通常载荷和变形成直线关系(右图b)。

这种表示载荷与变形的关系的曲线称为弹簧的特性曲线。

对拉伸弹簧，如图<圆柱螺旋拉伸弹簧的特性曲线>所示，图b为无预应力的拉伸弹簧的特性曲线；图c为有预应力的拉伸弹簧的特性曲线。

右图a中的H0是压缩弹簧在没有承受外力时的自由长度。

弹簧在安装时，通常预加一个压力F min，使它可靠地稳定在安装位置上。

F min称为弹簧的最小载荷(安装载荷)。

在它的作用下，弹簧的长度被压缩到H1其压缩变形量为λmin。

F max为弹簧承受的最大工作载荷。

在F max作用下，弹簧长度减到H2，其压缩变形量增到λmax。

λmax与λmin的差即为弹簧的工作行程圆柱螺旋压缩弹簧的特性曲线h,h=λmax-λmin。

F lim为弹簧的极限载荷。

在该力的作用下，弹簧丝内的应力达到了材料的弹性极限。

圆钢丝圆柱螺旋弹簧设计计算例题三、设计计算结果汇总：1、设计计算数据见表1表1 设计计算参数汇总表2、弹簧工作图样图1弹簧工作图技术要求a．弹簧端部形式：YI冷卷压缩弹簧；b．总圈数：n1 = 6.0圈；c．有效圈数：n = 4.0圈；d．旋向：右旋；e．强化处理：喷丸和立定处理；f．喷丸强度0.3 A ～ 0.45A，表面覆盖率大于90%；g．表面处理：清洗上防锈油；h．制造技术条件：其余按GB/T 1239.2二级精度。

2) 圆钢丝圆柱螺旋拉伸弹簧设计计算例题例2 :设计一拉伸弹簧，循环次数N =1.0×105次。

工作负荷F =160N,工作负荷下变形量为22mm，采用LⅢ圆钩环，外径D2=21mm。

一、题解分析：a)此拉伸弹簧要求循环次数N = 1.0×107次，由此说明弹簧是按有限寿命设计；b)题设给出了最大工作负荷及对应变形量：c)端部结构采用LⅢ圆钩环，即为圆勾环扭中心；d)弹簧外径D2 = 21mm。

二、解题方法：由以上分析可知，本题中未给出自由高度，说明自由高度可在满足其它条件下按实际计算而定，显然，本题是按表1中第一个设计计算条件及要求给出的。

方法1：严格设计法1）材料选取，根据弹簧使用的疲劳寿命要求，我们可选重要用途的碳素弹簧钢丝E 组别的钢丝，根据弹簧手册P345表10-16查得材料抗拉强度d b ln 3582072-=σ即本讲公式（2）中的 a = 2072；b = -358 从分析可知本弹簧按有限寿命使用，即由表3查得试验切应力的强度系 数为0.5×0.8 = 0.40即：b S στ4.0=；许用切应力系数36.08.045.0=⨯=κ即：b κστ=][ 2） 把题中给定的D = 21mm;F = 160N 及以上所选取的材料所查找的有关强度许用应力系数a = 2072；b = -358; 及36.0=κ代入本讲公式（2）：0)2)(ln ()08.054.64(2322222≤-+-+-d d D d b a d d D D F πκ化简得：05644808.439486.25)ln 35.849897.49185()ln 37.80938.4684(234≤+-+---d d d d d d解得：d ＞2.43 mm 取：d = 2.5mm ；此时，材料抗拉强度)5.2ln(3582072-=b σ=1744Mpa 而查标准附录7—表7.1得b σ= 1680Mpa ； 由此可见相对误差不到3.9%完全满足GB/5311标准的范围，因为标准给出的值按最低值给出。

最大拉力Pn N 120最小拉力P1N 60工作行程hmm 60弹簧外径D2mm 20载荷作用次数10^6I类：10^6以上,II类：10^3至10^6,III类：弹簧材料琴钢丝-D级端部结构圆钩环压中心初算弹簧刚度P'N/mm 1I类≥ 1.5Pn II类≥ 1.25225d D Pj fj328264.57.258有效圈数n 圈36弹簧刚度P’N/mm 1.011111111最小载荷下的变形量F1mm 35.30769231最大载荷下的变形量Fnmm 94.64835165极限载荷下的变形量Fj mm 245.6504093弹簧外径D2mm 31弹簧内径D1mm 25自由长度H0mm 167最小工作载荷下的长度H1mm 202.3076923最大工作载荷下的长度Hn mm 261.6483516极限工作载荷下的长度Hjmm 412.6504093节距t=d3展开长度Lmm 3298.672286实际极限变形量mm 178.021978最大工作载荷Pn N 120实际极限载荷PjN246.6718232180因为是拉伸弹簧，所以Pj要乘以0.8（Pn/0.8） 选择的是弹性特性验算螺旋角α°arctan0.034091417查表选取原始条件工作极限载荷Pj N 材料直径d及弹簧中径Dmm 参数计算弹簧工作时最大长度185自由长度125类：10^3至10^6,III类：10^3。

Pn III类≥1Pn 180P'dP0δb G 36.424.3211079000择的是I类载荷，取Pj=由于弹簧材料是琴钢丝D级，所以其修正arctan（t/pi*D)Pj fj308.33988.529528。

圆柱螺旋压缩（拉伸）弹簧的设计计算(一)几何参数计算普通圆柱螺旋弹簧的主要几何尺寸有：外径D、中径D2、内径D1、节距p、螺旋升角α及弹簧丝直径d。

由下图圆柱螺旋弹簧的几何尺寸参数图可知，它们的关系为：式中弹簧的螺旋升角α，对圆柱螺旋压缩弹簧一般应在5°～9°范围内选取。

弹簧的旋向可以是右旋或左旋，但无特殊要求时，一般都用右旋。

圆柱螺旋弹簧的几何尺寸参数普通圆柱螺旋压缩及拉伸弹簧的结构尺寸计算公式见表([color=#0000ff 普通圆柱螺旋压缩及拉伸弹簧的结构尺寸（mm）计算公式)。

普通圆柱螺旋压缩及拉伸弹簧的结构尺寸（mm）计算公式参数名称及代号计算公式备注压缩弹簧拉伸弹簧中径D2D2=Cd 按普通圆柱螺旋弹簧尺寸系列表取标准值内径D1D1=D2-d外径D D=D2+d旋绕比C C=D2/d 压缩弹簧长细比b b=H0/D2b在1～5.3的范围内选取自由高度或长度H0H0≈pn+(1.5～2)d（两端并紧，磨平）H0≈pn+(3～3.5)d（两端并紧，不磨H0=nd+钩环轴向长度平）工作高度或长度H1,H2,…,H nH n=H0-λn H n=H0+λnλn--工作变形量有效圈数n根据要求变形量按式（16-11）计算n≥2总圈数n1n1=n+(2～2.5)（冷卷）n1=n+(1.5～2)（YII型热卷）n1=n拉伸弹簧n1尾数为1/4,1/2,3/4整圈。

推荐用1/2圈节距p p=(0.28～0.5)D2p=d轴向间距δδ=p-d展开长度L L=πD2n1/cosαL≈πD2n+钩环展开长度螺旋角αα=arct g(p/πD2) 对压缩螺旋弹簧，推荐α=5°～9°质量m sm s=γ为材料的密度，对各种钢，γ=7700kg/；对铍青(二)特性曲线弹簧应具有经久不变的弹性，且不允许产生永久变形。

因此在设计弹簧时，务必使其工作应力在弹性极限范围内。

在这个范围内工作的压缩弹簧，当承受轴向载荷P时，弹簧将产生相应的弹性变形，如右图a所示。

圆柱螺旋弹簧计算
圆柱螺旋弹簧计算是指计算其弹性形变和力学特性，以提供制造、选型和使用的参考。

以下是圆柱螺旋弹簧计算的主要步骤：
1. 确定弹簧的几何参数。

这包括弹簧的直径、线径、圈数、自
由长度和最大挤压长度等参数。

2. 计算材料力学参数。

根据弹簧的材料性质，计算出其弹性模
量和剪切模量等参数。

3. 计算弹簧的刚度系数。

根据弹簧的几何参数和材料力学参数，计算出其刚度系数及其曲线。

4. 计算弹簧的永久形变。

由于弹簧在使用过程中会产生永久形变，因此需要计算其永久形变量。

5. 计算弹簧的载荷和挠度。

根据弹簧的几何参数、材料力学参
数和刚度系数，计算出其在不同载荷下的挠度和变形。

6. 选择适当的安全系数。

根据使用环境和要求，选择适当的安
全系数，以确保弹簧的安全性能和使用寿命。

7. 验证弹簧的性能。

通过实验或计算验证弹簧的载荷、挠度、
永久形变和疲劳特性等性能是否符合设计要求。

圆柱螺旋弹簧的计算涉及多个参数和变量，需要综合考虑弹簧
的几何形状、材料性质、载荷情况和安全系数等因素，以确保弹簧
的性能和使用安全。

1。

1. 弹簧刚度：
2. 力值： 其中：G 为材料剪切模量，一般不锈钢取71500Mpa,碳钢取
78500Mpa ；
d 为材料直径；
D 为弹簧中径；
n 为弹簧有效圈数；
f 为变形量（拉压行程）。

3. 应力： K 为曲度系数，公式为： 其中C 为弹簧旋绕比，是弹簧中径与线径的比值，即
4. 下表是GB/T23935-2009（圆柱螺旋弹簧设计计算）中压缩弹簧及拉伸弹簧的试验切应力及许用应力表
表2-1
n D d G 34
,
8P =f 8f 34,
⋅==n D Gd P P K PC K ⋅=⋅=2
3d 8d 8PD ππτC
C C K 615.04414+--=d D
C =
比压簧多了初拉力，加上初拉力就行。

初拉力： 其中初拉力τ0按初切应力图选取，见下图。

三．扭簧：
1.计算刚度 Dn
Ed M 3670'4= Nmm/° 2.扭矩 ϕ⋅=Dn
Ed M 36704
Nmm 式中:d---材料直径；
E---材料的弹性模量，一般不锈钢丝取188000Mpa ，碳素钢丝
取206000Mpa ；
D---弹簧外径；
ϕ---弹簧的扭转行程（角度）；
4. 应力： K1为曲度系数，顺旋向扭转取1，逆旋向扭转时按下式：
308τπ⋅=D d P 132
.10K d
M ⋅=σ
下表是GB/T23935-2009（圆柱螺旋弹簧设计计算）中扭转弹簧的试验切应力及许用应力表
C
C C C K 4414221---=。