高中数学第二章基本初等函数Ⅰ周练卷5新人教版必修11

新课程标准数学必修1第二章课后习题解答第二章 基本初等函数（I ） 2．1指数函数 练习（P54）1. a 21=a ,a 43=43a ,a53-=531a,a32-=321a.2. (1)32x =x 32, (2)43)(b a +=(a +b )43, (3)32n)-(m =(m -n )32, (4)4n)-(m =(m -n )2,(5)56q p =p 3q 25,(6)mm 3=m213-=m 25.3. (1)(4936)23=［(76)2］23=(76)3=343216;(2)23×35.1×612=2×321×(23)31×(3×22)61=231311--×3613121++=2×3=6;(3)a 21a 41a 81-=a814121-+=a 85; (4)2x31-(21x 31-2x 32-)=x 3131+--4x 3221--=1-4x -1=1x4-. 练习（P58）1.如图图2-1-2-142.(1)要使函数有意义,需x -2≥0,即x ≥2,所以函数y =32-x 的定义域为｛x |x ≥2｝;(2)要使函数有意义,需x ≠0,即函数y =(21)x 1的定义域是｛x ∣x ≠0｝.3.y =2x (x ∈N *)习题2.1 A 组（P59）1.(1)100;(2)-0.1;(3)4-π;(4)x -y .2解：(1)623b a ab=212162122123)(⨯⨯⨯b a a b =23232121--⨯b a =a 0b 0=1. (2)a aa2121=212121a a a⨯=2121a a ⨯=a 21.(3)415643)(mm m m m •••=4165413121mm m m m ••=4165413121+++mm=m 0=1.点评：遇到多重根号的式子,可以由里向外依次去掉根号,也可根据幂的运算性质来进行. 3.解：对于（1）,可先按底数5,再按键,再按12,最后按,即可求得它的值.答案：1.710 0; 对于（2）,先按底数8.31,再按键,再按12,最后按即可. 答案：2.881 0; 对于（3）这种无理指数幂,先按底数3,再按键,再按键,再按2,最后按即可.答案：4.728 8;对于（4）这种无理指数幂,可先按底数2,其次按键,再按π键,最后按即可.答案：8.825 0.4.解：(1)a 31a 43a127=a 1274331++=a 35; (2)a 32a 43÷a 65=a654332-+=a 127;(3)(x 31y43-)12=12431231⨯-⨯yx =x 4y -9;(4)4a 32b 31-÷(32-a 31-b 31-)=(32-×4)31313132+-+b a =-6ab 0=-6a ;(5))2516(462r t s -23-=)23(4)23(2)23(6)23(2)23(452-⨯-⨯-⨯--⨯-⨯rts=6393652----rt s =36964125s r r ;(6)(-2x 41y31-)(3x21-y 32)(-4x 41y 32)=［-2×3×(-4)］x 323231412141++-+-yx=24y ;(7)(2x 21+3y41-)(2x 21-3y41-)=(2x 21)2-(3y 41-)2=4x -9y 21-;(8)4x 41 (-3x 41y31-)÷(-6x21-y32-)=3231214141643+-++-⨯-y x =2xy 31. 点评：进行有理数指数幂的运算时,要严格按法则和运算顺序,同时注意运算结果的形式,但结果不能既有分数指数又有根式,也不能既有分母又有负指数.5.（1）要使函数有意义,需3-x ∈R ,即x ∈R ,所以函数y =23-x 的定义域为R . （2）要使函数有意义,需2x +1∈R ,即x ∈R ,所以函数y =32x +1的定义域为R .(3)要使函数有意义,需5x ∈R,即x ∈R,所以函数y =(21)5x的定义域为R . (4)要使函数有意义,需x ≠0,所以函数y =0.7x1的定义域为{x |x ≠0}.点评：求函数的定义域一是分式的分母不为零,二是偶次根号的被开方数大于零,0的0次幂没有意义.6.解：设经过x 年的产量为y ,一年内的产量是a (1+100p ),两年内产量是a (1+100p )2,…,x 年内的产量是a (1+100p )x ,则y =a (1+100p )x(x ∈N *,x ≤m ). 点评：根据实际问题,归纳是关键,注意x 的取值范围.7.(1)30.8与30.7的底数都是3,它们可以看成函数y =3x ,当x =0.8和0.7时的函数值；因为3>1,所以函数y =3x 在R 上是增函数.而0.7<0.8,所以30.7<30.8.(2)0.75-0.1与0.750.1的底数都是0.75,它们可以看成函数y =0.75x ,当x =-0.1和0.1时的函数值； 因为1>0.75,所以函数y =0.75x 在R 上是减函数.而-0.1<0.1,所以0.750.1<0.75-0.1.(3)1.012.7与1.013.5的底数都是1.01,它们可以看成函数y =1.01x ,当x =2.7和3.5时的函数值； 因为1.01>1,所以函数y =1.01x 在R 上是增函数.而2.7<3.5,所以1.012.7<1.013.5.(4)0.993.3与0.994.5的底数都是0.99,它们可以看成函数y =0.99x ,当x =3.3和4.5时的函数值； 因为0.99<1,所以函数y =0.99x 在R 上是减函数.而3.3<4.5,所以0.994.5<0.993.3.8.(1)2m ,2n 可以看成函数y =2x ,当x =m 和n 时的函数值;因为2>1,所以函数y =2x 在R 上是增函数.因为2m <2n ,所以m <n .(2)0.2m ,0.2n 可以看成函数y =0.2x ,当x =m 和n 时的函数值;因为0.2<1, 所以函数y =0.2x 在R 上是减函数.因为0.2m <0.2n ,所以m >n . (3)a m ,a n 可以看成函数y =a x ,当x =m 和n 时的函数值;因为0<a <1, 所以函数y =a x 在R 上是减函数.因为a m <a n ,所以m >n . (4)a m ,a n 可以看成函数y =a x ,当x =m 和n 时的函数值;因为a >1, 所以函数y =a x 在R 上是增函数.因为a m >a n ,所以m >n .点评：利用指数函数的单调性是解题的关键.9.(1)死亡生物组织内碳14的剩余量P 与时间t 的函数解析式为P=(21)57301.当时间经过九个“半衰期”后,死亡生物组织内的碳14的含量为P=(21)573057309⨯=(21)9≈0.002. 答:当时间经过九个“半衰期”后,死亡生物组织内的碳14的含量约为死亡前含量的2‰, 因此,还能用一般的放射性探测器测到碳14的存在.(2)设大约经过t 万年后,用一般的放射性探测器测不到碳14,那么(21)537010000t <0.001,解得t >5.7.答:大约经过6万年后,用一般的放射性探测器是测不到碳14的.B 组1. 当0＜a ＜1时,a 2x -7＞a 4x -12⇒x -7＜4x －1⇒x ＞－3;当a ＞1时,a 2x -7＞a 4x -1⇒2x －7＞4x －1⇒x ＜－3. 综上,当0＜a ＜1时,不等式的解集是{x |x ＞－3}；当a ＞1时,不等式的解集是{x |x ＜－3}.2.分析:像这种条件求值,一般考虑整体的思想,同时观察指数的特点,要注重完全平方公式的运用. 解：(1)设y =x 21+x21-,那么y 2=(x 21+x21-)2=x +x -1+2.由于x +x -1=3,所以y =5.(2)设y =x 2+x -2,那么y =(x +x -1)2-2.由于x +x -1=3,所以y =7.(3)设y =x 2-x -2,那么y =(x +x -1)(x -x -1),而(x -x -1)2=x 2-2+x -2=5,所以y =±35. 点评：整体代入和平方差,完全平方公式的灵活运用是解题的突破口. 3.解：已知本金为a 元.1期后的本利和为y 1=a +a ×r =a (1+r ),2期后的本利和为y 2=a (1+r )+a (1+r )×r =a (1+r )2, 3期后的本利和为y 3=a (1+r )3, …x 期后的本利和为y =a (1+r )x .将a =1 000,r =0.022 5,x =5代入上式得y =a (1+r )x =1 000×(1+0.022 5)5=1 000×1.02255≈1118. 答:本利和y 随存期x 变化的函数关系式为y =a (1+r )x ,5期后的本利和约为1 118元. 4.解：(1)因为y 1=y 2,所以a 3x +1=a -2x .所以3x +1=-2x .所以x =51-. (2)因为y 1>y 2,所以a 3x +1>a -2x . 所以当a >1时,3x +1>-2x .所以x >51-. 当0<a <1时,3x +1<-2x .所以x <51-.2．2对数函数 练习（P64）1.（1）2log 83=； （2）2log 325=； （3）21log 12=-； （4）2711log 33=- 2.（1）239=； （2）35125=； （3）2124-=； （4）41381-=3.（1）设5log 25x =，则25255x ==，所以2x =；（2）设21log 16x =，则412216x -==，所以4x =-； （3）设lg1000x =，则310100010x==，所以3x =； （4）设lg 0.001x =，则3100.00110x-==，所以3x =-；4.（1）1； （2）0； （3）2； （4）2； （5）3； （6）5.练习（P68）1.（1）lg()lg lg lg xyz x y z =++；（2）222lg lg()lg lg lg lg lg 2lg lg xy xy z x y z x y z z =-=++=++；（3）33311lg()lg lg lg lg 3lg lg22xy x y z x y z =-=+-=+-；（4）2211lg()lg (lg lg )lg 2lg lg 22y z x y z x y z ==-+=--. 2.（1）223433333log (279)log 27log 9log 3log 3347⨯=+=+=+=；（2）22lg1002lg1002lg104lg104====；（3）5lg 0.00001lg105lg105-==-=-; （4）11ln 22e ==3. (1)22226log 6log 3log log 213-===; (2)lg5lg 2lg101+==; (3)555511log 3log log (3)log 1033+=⨯==;(4)13333351log 5log 15log log log 31153--====-.4.(1)1; (2)1; (3)54练习（P73）1.函数3log y x =及13log y x =的图象如右图所示.相同点：图象都在y 轴的右侧，都过点(1,0) 不同点：3log y x =的图象是上升的，13log y x =的图象是下降的关系：3log y x =和13log y x =的图象是关于x 轴对称的.2. (1)(,1)-∞； (2)(0,1)(1,)+∞; （3）1(,)3-∞； （4）[1,)+∞3. (1)1010log 6log 8< (2)0.50.5log 6log 4< (3)2233log 0.5log 0.6> (4) 1.5 1.5log 1.6log 1.4>习题2.2 A 组（P74） 1. (1)3log 1x =； (2)41log 6x =; （3）4log 2x =； （4）2log 0.5x = (5) lg 25x = (6)5log 6x =2. (1)527x = (2) 87x = (3) 43x = (4)173x=(5) 100.3x= (6) 3xe =3. (1)0; (2) 2; (3) 2-; (4)2; (5) 14-; (6) 2. 4. (1)lg6lg 2lg3a b =+=+; (2) 3lg 42lg 22log 4lg3lg3ab===; (3) 2lg122lg 2lg3lg3log 1222lg 2lg 2lg 2b a +===+=+; (4)3lg lg3lg 22b a =-=- 5. (1)x ab =; (2) mx n=; (3) 3n x m =; (4)b x =.6. 设x 年后我国的GDP 在1999年的GDP 的基础上翻两番，则(10.073)4x+=解得 1.073log 420x =≈. 答：设20年后我国的GDP 在1999年的GDP 的基础上翻两番.7. (1)(0,)+∞; (2) 3(,1]4.8. (1)m n <; (2) m n <; (3) m n >; (4)m n >. 9. 若火箭的最大速度12000v =，那么62000ln 112000ln(1)61402M M M M e mm m m ⎛⎫+=⇒+=⇒+=⇒≈ ⎪⎝⎭答：当燃料质量约为火箭质量的402倍时，火箭的最大速度可达12km/s.10. (1)当底数全大于1时，在1x =的右侧，底数越大的图象越在下方.所以，①对应函数lg y x =，②对应函数5log y x =，③对应函数2log y x =. (2)略. (3)与原函数关于x 轴对称. 11. (1)235lg 25lg 4lg92lg52lg 22lg3log 25log 4log 98lg 2lg3lg5lg 2lg3lg5⋅⋅=⨯⨯=⨯⨯= (2)lg lg lg log log log 1lg lg lg a b c b c a b c a a b c⋅⋅=⨯⨯= 12. (1)令2700O =，则312700log 2100v =，解得 1.5v =. 答：鲑鱼的游速为1.5米/秒. (2)令0v =，则31log 02100O=，解得100O =. 答：一条鱼静止时的耗氧量为100个单位.B 组1. 由3log 41x =得：143,43xx-==，于是11044333x x -+=+= 2. ①当1a >时，3log 14a<恒成立； ②当01a <<时，由3log 1log 4a a a <=，得34a <，所以304a <<.综上所述：实数a 的取值范围是3{04a a <<或1}a >3. (1)当1I = W/m 2时，112110lg 12010L -==；(2)当1210I -= W/m 2时，121121010lg 010L --==答：常人听觉的声强级范围为0120dB .4. (1)由10x +>，10x ->得11x -<<，∴函数()()f x g x +的定义域为(1,1)- (2)根据(1)知：函数()()f x g x +的定义域为(1,1)-∴ 函数()()f x g x +的定义域关于原点对称又∵ ()()log (1)log (1)()()a a f x g x x x f x g x -+-=-++=+ ∴()()f x g x +是(1,1)-上的偶函数.5. (1)2log y x =，0.3log y x =； (2)3xy =，0.1x y =.习题2.3 A 组（P79） 1.函数y =21x是幂函数. 2.解析:设幂函数的解析式为f （x ）=x α,因为点（2,2）在图象上,所以2=2α.所以α=21,即幂函数的解析式为f （x ）=x 21,x ≥0.3.（1）因为流量速率v 与管道半径r 的四次方成正比,所以v =k ·r 4； （2）把r =3,v =400代入v =k ·r 4中,得k =43400＝81400,即v =81400r 4； （3）把r =5代入v =81400r 4,得v =81400×54≈3 086（cm 3/s ）, 即r =5 cm 时,该气体的流量速率为3 086 cm 3/s .第二章 复习参考题A 组（P82）1.（1）11； （2）87； （3）10001； （4）259. 2.（1）原式=))(()()(212121212212122121b a b a b a b a -+++-=b a b b a a b b a a -++++-2121212122=ba b a -+)(2;（2）原式=))(()(1121----+-a a a a a a =aa a a 11+-=1122+-a a . 3.（1）因为lg 2=a ,lg 3=b ,log 125=12lg 5lg =32lg 210lg2•=3lg 2lg 22lg 1+-,所以log 125=ba a +-21. （2）因为2log 3a =，3log 7b =37147log 27log 56log 27⨯=⨯=2log 112log 377++=7log 2log 11)7log 2(log 33333÷++÷=b ab a ÷++÷111)1(3=13++ab ab . 4.（1）（-∞,21）∪（21,+∞）;（2）［0,+∞）.5.（32,1）∪（1,+∞）;（2）（-∞,2）;（3）（-∞,1）∪（1,+∞）.6.（1）因为log 67>log 66=1,所以log 67>1.又因为log 76<log 77=1,所以log 76<1.所以log 67>log 76. （2）因为log 3π>log 33=1,所以log 3π>1.又因为log 20.8<0,所以log 3π>log 20.8.7.证明：（1）因为f （x ）=3x ,所以f （x ）·f （y ）=3x ×3y =3x +y .又因为f （x +y ）=3x +y ,所以f （x ）·f （y ）=f （x +y ）. （2）因为f （x ）=3x ,所以f （x ）÷f （y ）=3x ÷3y =3x -y . 又因为f （x -y ）=3x -y ,所以f （x ）÷f （y ）=f （x -y ）.8.证明:因为f （x ）=lgxx+-11,a 、b ∈（-1,1）, 所以f （a ）+f （b ）=lgbb a a +-++-11lg11=lg )1)(1()1)(1(b a b a ++--, f （ab b a ++1）=lg （ab b a ab ba +++++-1111）=lg b a ab b a ab +++--+11=lg )1)(1()1)(1(b a b a ++--. 所以f （a ）+f （b ）=f （abba ++1）.9.（1）设保鲜时间y 关于储藏温度x 的函数解析式为y =k ·a x （a >0,且a ≠1）.因为点（0,192）、（22,42）在函数图象上,所以022192,42,k a k a ⎧=⋅⎪⎨=⋅⎪⎩解得⎪⎩⎪⎨⎧≈==.93.0327,19222a k 所以y =192×0.93x ,即所求函数解析式为y =192×0.93x . （2）当x =30 ℃时,y ≈22（小时）；当x =16 ℃时,y ≈60（小时）,即温度在30 ℃和16 ℃的保鲜时间约为22小时和60小时. （3）图象如图：图2-210.解析：设所求幂函数的解析式为f （x ）=x α,因为f （x ）的图象过点（2,22）, 所以22=2α,即221-=2α.所以α=21-.所以f （x ）=x 21-（x >0）.图略,f (x )为非奇非偶函数；同时它在（0,+∞）上是减函数.B 组1.A2.因为2a =5b =10,所以a =log 210,b =log 510,所以a 1+b 1=10log 12+10log 15=lg 2+lg 5=lg 10=1. 3.（1）f （x ）=a 122+-x在x ∈（-∞,+∞）上是增函数.证明：任取x 1,x 2∈（-∞,+∞）,且x 1<x 2.f （x 1）-f （x 2）=a 122+-x -a +1222+x =1222+x -1221+x =)12)(12()22(21221++-x x x x . 因为x 1,x 2∈（-∞,+∞）, 所以.012.01212>+>+x x又因为x 1<x 2, 所以2122x x <即2122x x <<0.所以f （x 1）-f （x 2）<0,即f （x 1）<f （x 2）.所以函数f （x ）=a 122+-x在（-∞,+∞）上是增函数. （2）假设存在实数a 使f （x ）为奇函数,则f （-x ）+f （x ）=0,即a 121+--x +a 122+-x =0⇒a =121+-x +121+x =122+x +121+x=1, 即存在实数a =1使f （x ）=121+--x 为奇函数.4.证明:（1）因为f （x ）=2x x e e --,g （x ）=2xx e e -+,所以［g （x ）］2-［f （x ）］2=［g （x ）+f （x ）］［g （x ）-f （x ）］=)22)(22(xx x x x x x x e e e e e e e e -----++++ =e x ·e -x =e x -x =e 0=1, 即原式得证.（2）因为f （x ）=2x x e e --,g （x ）=2xx e e -+,所以f （2x ）=222x x e e -+,2f （x ）·g （x ）=2·2x x e e --·2x x e e -+=222xx e e --.所以f （2x ）=2f （x ）·g （x ）.（3）因为f （x ）=2x x e e --,g （x ）=2xx e e -+,所以g （2x ）=222x x e e -+,［g （x ）］2+［f （x ）］2=（2x x ee -+）2+（2xx e e --）2=4222222x x x x e e e e --+-+++=222xx e e -+.所以g （2x ）=［f （x ）］2+［g （x ）］2.5.由题意可知,θ1=62,θ0=15,当t =1时,θ=52,于是52=15+(62-15)e -k ,解得k ≈0.24,那么θ=15+47e -0.24t . 所以,当θ=42时,t ≈2.3;当θ=32时,t ≈4.2.答:开始冷却2.3和4.2小时后,物体的温度分别为42 ℃和32 ℃.物体不会冷却到12 ℃.6.(1)由P=P 0e -k t 可知,当t =0时,P=P 0;当t =5时,P=(1-10%）P 0.于是有(1-10%)P 0=P 0e -5k ,解得k =51-ln 0.9,那么P=P 0e t )9.0ln 51(.所以,当t =10时,P=P 0e 9.01051n I ⨯⨯=P 0e ln 0.81=81%P 0.答:10小时后还剩81%的污染物. (2)当P=50%P 0时,有50%P 0=P 0et )9.0ln 51(,解得t =9.0ln 515.0ln ≈33.答:污染减少50%需要花大约33h . (3)其图象大致如下:图2-3。

第1课时 对数函数的图象及性质知识点一 对数函数的概念函数y ＝log a x (a >0，且a ≠1)叫做对数函数，其中x 是自变量，函数的定义域是{x |x >0}． 形如y ＝2log 2x ，y ＝log 2x3都不是对数函数，可称其为对数型函数．知识点二 对数函数的图象与性质a >1 0<a <1图 象性 质定义域(0，＋∞)值域R过点(1,0)，即当x ＝1时，y ＝0在(0，＋∞)上是增函数在(0，＋∞)上是减函数底数a 与1的大小关系决定了对数函数图象的“升降”：当a ＞1时，对数函数的图象“上升”；当0＜a ＜1时，对数函数的图象“下降”．知识点三 反函数指数函数y ＝a x和对数函数y ＝log a x (a ＞0且a ≠1)互为反函数．[小试身手]1．判断(正确的打“√”，错误的打“×”) (1)对数函数的定义域为R .( )(2)y ＝log 2x 2与log x 3都不是对数函数．( ) (3)对数函数的图象一定在y 轴右侧．( ) (4)函数y ＝log 2x 与y ＝x 2互为反函数．( )答案：(1)× (2)√ (3)√ (4)× 2．下列函数中是对数函数的是( ) A ．y ＝log 14x B ．y ＝log 14(x ＋1)C ．y ＝2log 14x D ．y ＝log 14x ＋1解析：形如y ＝log a x (a >0，且a ≠1)的函数才是对数函数，只有A 是对数函数． 答案：A3．函数y ＝x ln(1－x )的定义域为( ) A ．(0,1) B ．[0,1) C ．(0,1] D ．[0,1]解析：由题意，得⎩⎪⎨⎪⎧x ≥0，1－x >0，解得0≤x <1；故函数y ＝x ln(1－x )的定义域为[0,1)．答案：B4．若f (x )＝log 2x ，x ∈[2,3]，则函数f (x )的值域为________． 解析：因为f (x )＝log 2x 在[2,3]上是单调递增的， 所以log 22≤log 2x ≤log 23， 即1≤log 2x ≤log 23. 答案：[1，log 23]类型一 对数函数的概念例1 下列函数中，哪些是对数函数？ (1)y ＝log a x (a >0，且a ≠1)； (2)y ＝log 2x ＋2； (3)y ＝8log 2(x ＋1)； (4)y ＝log x 6(x >0，且x ≠1)； (5)y ＝log 6x .【解析】 (1)中真数不是自变量x ，不是对数函数．(2)中对数式后加2，所以不是对数函数．(3)中真数为x ＋1，不是x ，系数不为1，故不是对数函数．(4)中底数是自变量x ，而非常数，所以不是对数函数．(5)中底数是6，真数为x ，系数为1，符合对数函数的定义，故是对数函数．用对数函数的概念例如y ＝log a x(a ＞0且a≠0)来判断． 方法归纳判断一个函数是对数函数的方法跟踪训练1 若函数f (x )＝(a 2－a ＋1)log (a ＋1)x 是对数函数，则实数a ＝________. 解析：由a 2－a ＋1＝1，解得a ＝0或a ＝1. 又底数a ＋1>0，且a ＋1≠1，所以a ＝1. 答案：1,对数函数y ＝log a x 系数为1. 类型二 求函数的定义域 例2 求下列函数的定义域： (1)y ＝lg(x ＋1)＋3x21－x；(2)y ＝log (x －2)(5－x )．【解析】 (1)要使函数有意义，需⎩⎪⎨⎪⎧x ＋1>0，1－x >0，即⎩⎪⎨⎪⎧x >－1，x <1.∴－1<x <1，∴函数的定义域为(－1,1)． (2)要使函数有意义，需⎩⎪⎨⎪⎧ 5－x >0，x －2>0，x －2≠1，∴⎩⎪⎨⎪⎧x <5，x >2，x ≠3.∴定义域为(2,3)∪(3,5)．,真数大于0，偶次根式被开方数大于等于0，分母不等于0，列不等式组求解．方法归纳求定义域有两种题型，一种是已知函数解析式求定义域，常规为：分母不为0；0的零次幂与负指数次幂无意义；偶次根式被开方式(数)非负；对数的真数大于0，底数大于0且不等于1.另一种是抽象函数的定义域问题．同时应注意求函数定义域的解题步骤．跟踪训练2 函数y ＝log 0.5x －5的定义域是( ) A ．(0，＋∞) B ．(5,6] C ．(5，＋∞) D ．(－∞，6]解析：由⎩⎪⎨⎪⎧x －5>0，log 0.5x －5≥0，得⎩⎪⎨⎪⎧x >5，x －5≤1，∴5<x ≤6，∴定义域为(5,6]． 答案：B ,真数大于0，偶次根式被开方数大于等于0. 类型三 对数函数的图象问题例3 (1)函数y ＝x ＋a 与y ＝log a x 的图象只可能是下图中的( )(2)已知函数y ＝log a (x ＋3)－1(a ＞0，a ≠1)的图象恒过定点A ，若点A 也在函数f (x )＝3x＋b 的图象上，则f (log 32)＝________.(3)如图所示的曲线是对数函数y ＝log a x ，y ＝log b x ，y ＝log c x ，y ＝log d x 的图象，则a ，b ，c ，d 与1的大小关系为________．【解析】 (1)A 中，由y ＝x ＋a 的图象知a ＞1，而y ＝log a x 为减函数，A 错；B 中，0＜a ＜1，而y ＝log a x 为增函数，B 错；C 中，0＜a ＜1，且y ＝log a x 为减函数，所以C 对；D 中，a ＜0，而y ＝log a x 无意义，也不对．(2)依题意可知定点A (－2，－1)，f (－2)＝3－2＋b ＝－1，b ＝－109，故f (x )＝3x－109，f (log 32)＝3log 32－109＝2－109＝89.(3)由题干图可知函数y ＝log a x ，y ＝log b x 的底数a ＞1，b ＞1，函数y ＝log c x ，y ＝log d x 的底数0＜c ＜1,0＜d ＜1.过点(0,1)作平行于x 轴的直线，则直线与四条曲线交点的横坐标从左向右依次为c ，d ，a ，b ，显然b ＞a ＞1＞d ＞c .【答案】 (1)C (2)89 (3)b ＞a ＞1＞d ＞c(1)由函数y ＝x ＋a 的图象判断出a 的范围． (2)依据log a 1＝0，a 0＝1，求定点坐标．(3)沿直线y ＝1自左向右看，对数函数的底数由小变大． 方法归纳解决对数函数图象的问题时要注意(1)明确对数函数图象的分布区域．对数函数的图象在第一、四象限．当x 趋近于0时，函数图象会越来越靠近y 轴，但永远不会与y 轴相交．(2)建立分类讨论的思想．在画对数函数图象之前要先判断对数的底数a 的取值范围是a >1，还是0<a <1.(3)牢记特殊点．对数函数y ＝log a x (a >0，且a ≠1)的图象经过点：(1,0)，(a,1)和⎝ ⎛⎭⎪⎫1a ，－1.跟踪训练3(1)如图所示，曲线是对数函数y ＝log a x (a >0，且a ≠1)的图象，已知a 取3，43，35，110，则相应于C 1，C 2，C 3，C 4的a 值依次为( )A.3，43，35，110B.3，43，110，35C.43，3，35，110D.43，3，110，35(2)函数y ＝log a |x |＋1(0<a <1)的图象大致为( )解析：(1)方法一 作直线y ＝1与四条曲线交于四点，由y ＝log a x ＝1，得x ＝a (即交点的横坐标等于底数)，所以横坐标小的底数小，所以C 1，C 2，C 3，C 4对应的a 值分别为3，43，35，110，故选A. 方法二 由对数函数的图象在第一象限内符合底大图右的规律，所以底数a 由大到小依次为C 1，C 2，C 3，C 4，即3，43，35，110.故选A.(2)函数为偶函数，在(0，＋∞)上为减函数，(－∞，0)上为增函数，故可排除选项B ，C ，又x ＝±1时y ＝1，故选A.答案：(1)A (2)A(1)增函数底数a ＞1， 减函数底数0＜a ＜1.(2)先去绝对值，再利用单调性判断.[基础巩固](25分钟，60分)一、选择题(每小题5分，共25分) 1．下列函数是对数函数的是( ) A ．y ＝2＋log 3xB ．y ＝log a (2a )(a ＞0，且a ≠1)C ．y ＝log a x 2(a ＞0，且a ≠1) D ．y ＝ln x解析：判断一个函数是否为对数函数，其关键是看其是否具有“y ＝log a x ”的形式，A ，B，C全错，D正确．答案：D2．若某对数函数的图象过点(4,2)，则该对数函数的解析式为( )A．y＝log2x B．y＝2log4xC．y＝log2x或y＝2log4x D．不确定解析：由对数函数的概念可设该函数的解析式为y＝log a x(a>0，且a≠1，x>0)，则2＝log a4＝log a22＝2log a2，即log a2＝1，a＝2.故所求解析式为y＝log2x.答案：A3．设函数y＝4－x2的定义域为A，函数y＝ln(1－x)的定义域为B，则A∩B＝( ) A．(1,2) B．(1,2]C．(－2,1) D．[－2,1)解析：由题意可知A＝{x|－2≤x≤2}，B＝{x|x＜1}，故A∩B＝{x|－2≤x＜1}．答案：D4．函数y＝e x的图象与函数y＝f(x)的图象关于直线y＝x对称，则( )A．f(x)＝lg x B．f(x)＝log2xC．f(x)＝ln x D．f(x)＝x e解析：易知y＝f(x)是y＝e x的反函数，所以f(x)＝ln x.答案：C5．已知a＞0，且a≠1，函数y＝a x与y＝log a(－x)的图象只能是下图中的( )解析：由函数y＝log a(－x)有意义，知x＜0，所以对数函数的图象应在y轴左侧，可排除A，C.又当a＞1时，y＝a x为增函数，所以图象B适合．答案：B二、填空题(每小题5分，共15分)6．若f(x)＝log a x＋(a2－4a－5)是对数函数，则a＝________.解析：由对数函数的定义可知⎩⎪⎨⎪⎧a 2－4a －5＝0a >0a ≠1，∴a ＝5.答案：57．已知函数f (x )＝log 3x ，则f ⎝ ⎛⎭⎪⎫95＋f (15)＝________.解析：f ⎝ ⎛⎭⎪⎫95＋f (15)＝log 395＋log 315＝log 327＝3.答案：38．函数f (x )＝log a (2x －3)(a ＞0且a ≠1)，的图象恒过定点P ，则P 点的坐标是________． 解析：令2x －3＝1，解得x ＝2，且f (2)＝log a 1＝0恒成立，所以函数f (x )的图象恒过定点P (2,0)．答案：(2,0)三、解答题(每小题10分，共20分) 9．求下列函数的定义域： (1)y ＝log 3(1－x )； (2)y ＝1log 2x ；(3)y ＝log 711－3x.解析：(1)∵当1－x >0，即x <1时， 函数y ＝log 3(1－x )有意义，∴函数y ＝log 3(1－x )的定义域为(－∞，1)． (2)由log 2x ≠0，得x >0且x ≠1.∴函数y ＝1log 2x 的定义域为{x |x >0且x ≠1}．(3)由11－3x >0，得x <13.∴函数y ＝log 711－3x 的定义域为⎝ ⎛⎭⎪⎫－∞，13.10．求出下列函数的反函数： (1)y ＝log 16x ；(2)y ＝⎝ ⎛⎭⎪⎫1e x；(3)y ＝πx.解析：(1)对数函数y ＝log 16x ，它的底数为16，所以它的反函数是指数函数y ＝⎝ ⎛⎭⎪⎫16x；(2)同理，指数函数y ＝⎝ ⎛⎭⎪⎫1e x的反函数是对数函数y ＝log 1ex ；(3)指数函数y ＝πx的反函数为对数函数y ＝log πx .[能力提升](20分钟，40分)11．已知函数f (x )＝a x(a >0，a ≠1)的反函数为g (x )，且满足g (2)<0，则函数g (x ＋1)的图象是下图中的( )解析：由y ＝a x解得x ＝log a y ， ∴g (x )＝log a x . 又∵g (2)<0，∴0<a <1.故g (x ＋1)＝log a (x ＋1)是递减的，并且是由函数g (x )＝log a x 向左平移1个单位得到的． 答案：A12．函数f (x )＝ln x ＋31－2x的定义域是________．解析：∵f (x )＝lnx ＋31－2x，∴要使函数f (x )有意义，需使⎩⎪⎨⎪⎧x ＋3>01－2x>0，即－3<x <0.答案：(－3,0)13．已知函数y ＝log 2x 的图象，如何得到y ＝log 2(x ＋1)的图象？y ＝log 2(x ＋1)的定义域与值域是多少？与x 轴的交点是什么？解析：y ＝log 2x ―――――→左移1个单位y ＝log 2(x ＋1)，如图．定义域为(－1，＋∞)，值域为R ，与x 轴的交点是(0,0)．14．已知函数f (x )＝log 2x －1的定义域为A ，函数g (x )＝⎝ ⎛⎭⎪⎫12x(－1≤x ≤0)的值域为B .(1)求A ∩B ；(2)若C ＝{y |y ≤a －1}，且B ⊆C ，求a 的取值范围． 解析：(1)由题意知：⎩⎪⎨⎪⎧x －1>0，log 2x －1≥0⇒x ≥2，所以A ＝{x |x ≥2}，B ＝{y |1≤y ≤2}， 所以A ∩B ＝{2}．(2)由(1)知B ＝{y |1≤y ≤2}，若要使B ⊆C ，则有a －1≥2，所以a ≥3. 即a 的取值范围为[3，＋∞)．。

课时23 对数的运算(2)换底公式的应用a b c abc A ．1 B ．2 C ．3 D ．5答案 A解析 ∵log a x ＝1log x a ＝2，∴log x a ＝12. 同理log x c ＝16，log x b ＝13. ∴log abc x ＝1log x abc ＝1log x a ＋log x b ＋log x c＝1. 2．若log 34·log 48·log 8m ＝log 416，则m ＝________.答案 9解析 由换底公式，得lg 4lg 3×lg 8lg 4×lg m lg 8＝lg m lg 3＝log 416＝2，∴lg m ＝2lg 3＝lg 9，∴m ＝9.3．设3x ＝4y ＝36，求2x ＋1y的值． 解 由已知分别求出x 和y ，∵3x ＝36,4y＝36，∴x ＝log 336，y ＝log 436，由换底公式得： x ＝log 3636log 363＝1log 363，y ＝log 3636log 364＝1log 364， ∴1x ＝log 363，1y＝log 364， ∴2x ＋1y＝2log 363＋log 364＝log 36(32×4)＝log 3636＝1. 4．计算：(1)log 89×log 2732；(2)log 927；(3)log 21125×log 3132×log 513； (4)(log 43＋log 83)(log 32＋log 92)．解 (1)log 89×log 2732＝lg 9lg 8×lg 32lg 27＝lg 32lg 23×lg 25lg 33＝2lg 33lg 2×5lg 23lg 3＝109； (2)log 927＝log 327log 39＝log 333log 332＝3log 332log 33＝32； (3)log 21125×log 3132×log 513＝log 25－3×log 32－5×log 53－1＝－3log 25×(－5log 32)×(－log 53)＝－15×lg 5lg 2×lg 2lg 3×lg 3lg 5＝－15； (4)原式＝⎝⎛⎭⎪⎫lg 3lg 4＋lg 3lg 8⎝ ⎛⎭⎪⎫lg 2lg 3＋lg 2lg 9 ＝⎝ ⎛⎭⎪⎫lg 32lg 2＋lg 33lg 2⎝ ⎛⎭⎪⎫lg 2lg 3＋lg 22lg 3 ＝12＋14＋13＋16＝54.运用换底公式不熟练致误23A.14 B.12C ．2D ．4 易错分析 本题易在使用对数的运算公式时，尤其换底公式的使用过程中发生错误． 答案 D正解 log 29×log 34＝lg 9lg 2×lg 4lg 3＝2lg 3lg 2×2lg 2lg 3＝2×2＝4.一、选择题1.log 29log 23＝( )A.12 B ．2 C.32 D.92答案 B解析 由换底公式log 39＝log 29log 23.∵log 39＝2，∴log 29log 23＝2.2．已知log 23＝a ，log 37＝b ，则log 27＝() A ．a ＋b B ．a －b C ．ab D.ab答案 C解析 log 27＝log 23×log 37＝ab .3．设2a ＝5b ＝m ，且1a ＋1b ＝2，则m ＝( ) A.10 B ．10 C ．20 D ．100答案 A解析 ∵2a ＝5b ＝m ，∴a ＝log 2m ，b ＝log 5m .1a ＋1b ＝log m 2＋log m 5＝log m 10＝2，∴m 2＝10.又∵m >0，∴m ＝10，选A.4.1log 1419＋1log 1513等于( )A ．lg 3B ．－lg 3C.1lg 3 D ．－1lg 3答案 C解析 原式＝log 1914＋log 1315＝log 1312＋log 1315＝log 13110＝log 310＝1lg 3.选C. 5．已知2a ＝3b ＝k (k ≠1)，且2a ＋b ＝ab ，则实数k 的值为( )A ．6B ．9C ．12D ．18答案 D解析 a ＝log 2k ，b ＝log 3k ，由2a ＋b ＝ab 得2log 2k ＋log 3k ＝log 2k ·log 3k ，即2lg k lg 2＋lg k lg 3＝k2lg 2lg 3，得2lg 3＋lg 2＝lg k ，即k ＝18.二、填空题6．方程log 3(x －1)＝log 9(x ＋5)的解是________．答案 4解析 由换底公式得log 9(x ＋5)＝12log 3(x ＋5)．∴原方程可化为2log 3(x －1)＝log 3(x ＋5)，即log 3(x －1)2＝log 3(x ＋5)，∴(x －1)2＝x ＋5.∴x 2－3x －4＝0，解得x ＝4或x ＝－1.又∵⎩⎪⎨⎪⎧ x －1>0，x ＋5>0，∴x >1，故x ＝4.7．若log a b ·log 3a ＝4，则b 的值为________．答案 81解析 log a b ·log 3a ＝4，即log 3a ·log a b ＝4，即log 3b ＝4，∴34＝b ，∴b ＝81.8．已知2x ＝72y ＝A ，且1x ＋1y ＝1，则A 的值是________．答案 98解析 ∵2x ＝72y ＝A ，∴x ＝log 2A,2y ＝log 7A .∴1x ＋1y ＝1log 2A ＋2log 7A＝log A 2＋2log A 7＝log A 2＋log A 49＝log A 98＝1.∴A ＝98.三、解答题9．计算下列各式的值：(1)lg 2＋lg 5－lg 8lg 5－lg 4；(2)lg 5(lg 8＋lg 1000)＋(lg 23)2＋lg 16＋lg 0.06. 解 (1)原式＝1－3lg 2lg 5－2lg 2＝1－3lg 21－3lg 2＝1； (2)原式＝lg 5(3lg 2＋3)＋3(lg 2)2－lg 6＋lg 6－2＝3lg 5×lg 2＋3lg 5＋3lg 22－2＝3lg 2(lg 5＋lg 2)＋3lg 5－2＝3(lg 2＋lg 5)－2＝3－2＝1.10．已知x ，y ，z 为正数，3x ＝4y ＝6z,2x ＝py .(1)求p ；(2)求证：1z －1x ＝12y. 解 (1)设3x ＝4y ＝6z ＝k (显然k >0，且k ≠1)，则x ＝log 3k ，y ＝log 4k ，z ＝log 6k .由2x ＝py ，得2log 3k ＝p log 4k ＝p ·log 3k log 34. ∵log 3k ≠0，∴p ＝2log 34.(2)证明：1z －1x ＝1log 6k －1log 3k ＝log k 6－log k 3＝log k 2＝12log k 4＝12y ，∴1z －1x ＝12y.►2.2.2 对数函数及其性质。

高中同步创优单元测评A 卷 数 学班级：________ 姓名：________ 得分：________第二章 基本初等函数(Ⅰ)(二) (对数与对数函数、幂函数)[名师原创·基础卷](时间：120分钟 满分：150分) 第Ⅰ卷 (选择题 共60分)一、选择题(本大题共12个小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的)1．函数f (x )＝lg(x －1)的定义域是( )A ．(2，＋∞)B ．(1，＋∞)C ．[1，＋∞)D ．[2，＋∞) 2．下列函数中，既是奇函数，又在定义域内为减函数的是( )A ．y ＝⎝ ⎛⎭⎪⎫12xB ．y ＝1x C ．y ＝－x 3D ．y ＝log 3(－x )3．设y 1＝，y 2＝log 12，y 3＝⎝ ⎛⎭⎪⎫13，则( )A ．y 3>y 1>y 2B ．y 2>y 1>y 3C ．y 1>y 2>y 3D ．y 1>y 3>y 24．函数y ＝⎝ ⎛⎭⎪⎫12x的反函数的图象为( )5．已知f (x n )＝ln x ，则f (2)的值为( ) A ．ln 2 ln 2 ln 2D ．2ln 26．幂函数y ＝(m 2－m －1)x m 2－2m －3，当x ∈(0，＋∞)时为减函数，则实数m 的值为( )A ．m ＝2B ．m ＝－1C ．m ＝－1或2D ．m ≠1±527．设函数f (x )＝⎩⎪⎨⎪⎧21－x ，x ≤1，1－log 2x ，x >1，则满足f (x )≤2的x 的取值范围是( )A ．[－1,2]B ．[0,2]C ．[1，＋∞)D ．[0，＋∞)8．若0<a <1，在区间(－1,0)上函数f (x )＝log a (x ＋1)是( ) A ．增函数且f (x )>0 B ．增函数且f (x )<0 C ．减函数且f (x )>0D ．减函数且f (x )<09．已知函数f (x )＝a x ＋log a x (a >0，且a ≠1)在[1,2]上的最大值与最小值之和为log a 2＋6，则a 的值为( )C ．2D ．410．若偶函数f (x )在(－∞，0)内单调递减，则不等式f (－1)<f (lg x )的解集是( ) A ．(0,10)∪(10，＋∞)11．已知f (x )＝a x (a >0，且a ≠1)，g (x )＝log a x (a >0，且a ≠1)，若f (3)g (3)<0，则f (x )与g (x )在同一平面直角坐标系内的图象可能是( )12．设f (x )是定义在(－∞，＋∞)上的偶函数，且它在[0，＋∞)上单调递增，若，c ＝f (－2)，则a ，b ，c 的大小关系是( )A ．a >b >cB ．b >c >aC ．c >a >bD ．c >b >a第Ⅱ卷 (非选择题 共90分)二、填空题(本大题共4个小题，每小题5分，共20分，请把正确答案填在题中横线上)13．若函数y ＝f (x )的定义域是⎣⎢⎡⎦⎥⎤12，2，则函数y ＝f (log 2x )的定义域为________． 14．给出函数f (x )＝⎩⎨⎧⎝ ⎛⎭⎪⎫12x ，x ≥4，f (x ＋1)，x <4，则f (log 23)＝________.15．已知函数y ＝log a (x ＋b )的图象如图所示，则a ＝________，b ＝________.16．设函数f (x )是定义在R 上的奇函数，若当x ∈(0，＋∞)时，f (x )＝lg x ，则满足f (x )>0的x 的取值范围是________．三、解答题(本大题共6个小题，共70分，解答时应写出必要的文字说明、证明过程或演算步骤)17．(本小题满分10分) 计算下列各题：18．(本小题满分12分)已知函数f (x )＝－2x 12. (1)求f (x )的定义域；(2)证明：f (x )在定义域内是减函数．19．(本小题满分12分)已知－3≤≤－32，求函数f (x )＝log 2x 2·log 2x4的最大值和最小值．20．(本小题满分12分)设f (x )＝⎩⎨⎧2－x，x ∈(－∞，1]，log 3x 3·log 3x9，x ∈(1，＋∞). (1)求f ⎝ ⎛⎭⎪⎫log 232的值；(2)求f (x )的最小值．21．(本小题满分12分)已知函数f(x)＝log a(1－x)＋log a(x＋3)，其中0<a<1.(1)求函数f(x)的定义域；(2)若函数f(x)的最小值为－4，求a的值．22．(本小题满分12分)已知函数f(x)＝log4(ax2＋2x＋3)(a∈R)．(1)若f(1)＝1，求f(x)的单调区间；(2)是否存在实数a，使f(x)的最小值为0？若存在，求出a的值；若不存在，请说明理由．详解答案第二章基本初等函数(Ⅰ)(二)(对数与对数函数、幂函数)[名师原创·基础卷]1．B 解析：由x －1>0，得x >1. 解题技巧：真数大于零．2．C 解析：y ＝⎝ ⎛⎭⎪⎫12x 与y ＝log 3(－x )都为非奇非偶，排除A ，＝1x 在(－∞，0)与(0，＋∞)上都为减函数，但在定义域内不是减函数，排除B.3．D 解析：因为y 1＝>40＝1，y 2＝log 12 <log 121＝0,0<y 3＝⎝ ⎛⎭⎪⎫13<⎝ ⎛⎭⎪⎫130＝1，所以y 1>y 3>y 2.4．D 解析：函数y ＝⎝ ⎛⎭⎪⎫12x的反函数为y ＝log 12x ，故选D.5．B 解析：令t ＝x n，则x ＝t 1n ，f (t )＝ln t 1n ＝1nln t ，则f (2)＝1n ln 2，故选B.6．A 解析：由y ＝(m 2－m －1)xm 2－2m －3为幂函数，得m 2－m －1＝1，解得m＝2或m ＝－1.当m ＝2时，m 2－2m －3＝－3，y ＝x －3在(0，＋∞)上为减函数；当m ＝－1时，m 2－2m －3＝0，y ＝x 0＝1(x ≠0)在(0，＋∞)上为常数函数(舍去)，所以m ＝2，故选A.7．D 解析：当x ≤1时，由21－x ≤2知，x ≥0，即0≤x ≤1； 当x >1时，由1－log 2x ≤2知x ≥12，即x >1. 综上得x 的取值范围是[0，＋∞)．8．C 解析：当0<a <1时，f (x )＝log a (x ＋1)为减函数，∵x ∈(－1,0)，∴x ＋1∈(0,1)，∴log a (x ＋1)>0.9．C 解析：当a >1时，函数y ＝a x 和y ＝log a x 在[1,2]上都是增函数， 所以f (x )＝a x ＋log a x 在[1,2]上是增函数，当0<a <1时，函数y ＝a x 和y ＝log a x 在[1,2]上都是减函数，所以f (x )＝a x ＋log a x 在[1,2]上是减函数，由题意得f (1)＋f (2)＝a ＋a 2＋log a 2＝6＋log a 2， 即a ＋a 2＝6，解得a ＝2或a ＝－3(舍去)．10．D 解析：因为f (x )为偶函数，所以f (x )＝f (|x |)，因为f (x )在(－∞，0)内单调递减，所以f (x )在(0，＋∞)内单调递增，由f (－1)<f (lg x )，得|lg x |>1，即lg x >1或lg x <－1，解得x >10或0<x <110.11．C 解析：∵f (3)＝a 3>0，由f (3)·g (3)<0得g (3)<0， ∴0<a <1，∴f (x )与g (x )均为单调递减函数，故选C.13．[2，4] 解析：由题意知，12≤log 2x ≤2，即log 22≤log 2x ≤log 24， ∴2≤x ≤4.解析：∵log 23<4，∴f (log 23)＝f (log 23＋1)＝f (log 23＋3)＝f (log 224)，∵log 224>4，∴f (log 224)＝⎝ ⎛⎭⎪⎫12log 224＝124.3 解析：由图象过点(－2,0)，(0,2)，知⎩⎨⎧log a (－2＋b )＝0，log a b ＝2，∴⎩⎨⎧－2＋b ＝1，b ＝a 2.解得⎩⎨⎧b ＝3，a 2＝3.由a >0，知a ＝ 3.∴a ＝3，b ＝3.16．(－1,0)∪(1，＋∞) 解析：根据题意画出f (x )的草图，由图象可知，f (x )>0的x 的取值范围是－1<x <0或x >1.解题技巧：数形结合确定取值范围．19．解：∵f (x )＝log 2x 2·log 2x4 ＝(log 2x －1)(log 2x －2) ＝(log 2x )2－3log 2x ＋2 ＝⎝ ⎛⎭⎪⎫log 2x －322－14， 又∵ －3≤≤－32， ∴ －3≤log 12 x ≤－32.∴ 32≤log 2x ≤3.∴当log 2x ＝32，即x ＝22时，f (x )有最小值－14； 当log 2x ＝3，即x ＝8时，f (x )有最大值2. 20．解：(1)因为log 232<log 22＝1，(2)当x ∈(－∞，1]时，f (x )＝2－x ＝⎝ ⎛⎭⎪⎫12x 在(－∞，1]上是减函数，所以f (x )的最小值为f (1)＝12.当x ∈(1，＋∞)时，f (x )＝(log 3x －1)(log 3x －2)， 令t ＝log 3x ，则t ∈(0，＋∞)，f (x )＝g (t )＝(t －1)(t －2)＝⎝⎛⎭⎪⎫t －322－14，所以f (x )的最小值为g ⎝ ⎛⎭⎪⎫32＝－14.综上知，f (x )的最小值为－14. 21．解：(1)要使函数有意义，则有⎩⎪⎨⎪⎧1－x >0，x ＋3>0，解之得－3<x <1，所以函数的定义域为(－3,1)． (2)函数可化为f (x )＝log a [(1－x )(x ＋3)] ＝log a (－x 2－2x ＋3) ＝log a [－(x ＋1)2＋4]，∵－3<x <1，∴0<－(x ＋1)2＋4≤4. ∵0<a <1，∴log a [－(x ＋1)2＋4]≥log a 4， 即f (x )min ＝log a 4.由log a 4＝－4，得a －4＝4，∴a ＝4－14＝22.22．解：(1)∵f (1)＝1，∴log 4(a ＋5)＝1，因此a ＋5＝4，a ＝－1， 这时f (x )＝log 4(－x 2＋2x ＋3)．由－x 2＋2x ＋3>0，得－1<x <3，函数定义域为(－1,3)． ∴f (x )的单调递增区间是(－1,1)，单调递减区间是(1,3)．(2)假设存在实数a ，使f (x )的最小值为0，则h (x )＝ax 2＋2x ＋3应有最小值1，因此应有⎩⎨⎧ a >0，12a －44a ＝1，解得a ＝12. 故存在实数a ＝12，使f (x )的最小值为0.解题技巧：存在性问题的求解办法：先假设符合题意的实数存在，从这个假设出发，利用已知条件看看能不能求出这个实数．。

高中数学学习材料金戈铁骑整理制作第11讲 §2.1.1 指数与指数幂的运算¤学习目标：理解有理指数幂的含义，通过具体实例了解实数指数幂的意义，掌握根式与分数指数幂的互化，掌握有理数指数幂的运算.¤知识要点：1. 若n x a =，则x 叫做a 的n 次方根，记为n a ，其中n >1，且n N *∈. n 次方根具有如下性质：（1）在实数范围内，正数的奇次方根是一个正数，负数的奇次方根是一个负数；正数的偶次方根是两个绝对值相等、符号相反的数，负数的偶次方根没有意义；零的任何次方根都是零.（2）n 次方根（*1,n n N >∈且）有如下恒等式：()n n a a =；,||,n n a n a a n ⎧=⎨⎩为奇数为偶数；np n mp m a a =，（a ≥0）. 2. 规定正数的分数指数幂：mn m na a = （0,,,1a m n N n *>∈>且）； 11m nm nmna aa-==.¤例题精讲：【例1】求下列各式的值：（1）3n nπ-（）（*1,n n N >∈且）； （2）2()x y -. 解：（1）当n 为奇数时，33n n ππ-=-（）；当n 为偶数时，3|3|3n nπππ-=-=-（）.（2）2()||x y x y -=-.当x y ≥时，2()x y x y -=-；当x y <时，2()x y y x -=-.【例2】已知221na =+，求33n n n na a a a--++的值. 解：332222()(1)1121122121n n n n n n n n nn n na a a a a a a a a a a a ------++-+==-+=+-+=-+++. 【例3】化简：（1）211511336622(2)(6)(3)a b a b a b -÷-； （2）3322114423()a b ab ba b a⋅（a ＞0，b ＞0）； （3）243819⨯.解：（1）原式=2111150326236[2(6)(3)]44a bab a +-+-⨯-÷-==.（2）原式=1312322123[()](/)a b ab ab b a ⋅⋅=1136322733a b a b a b⋅=104632733a b a b=a b. （3）原式=2212124444244332323[(3)]3333⨯⨯⨯=⨯=⨯221111446336444(33)(3)(3)3333=⨯=⨯=⨯=.点评：根式化分数指数幂时，切记不能混淆，注意将根指数化为分母，幂指数化为分子，根号的嵌套，化为幂的幂. 正确转化和运用幂的运算性质，是复杂根式化简的关键.【例4】化简与求值：（1）642642++-； （2）11111335572121n n +++⋅⋅⋅++++-++.解：（1）原式=22222222(2)2222(2)+⨯⨯++-⨯⨯+ =22(22)(22)++- =2222++-=4. （2）原式=3153752121315375(21)(21)n n n n ---+--+++⋅⋅⋅+---+-- =1(3153752121)2n n -+-+-+⋅⋅⋅++--=1(211)2n +-.点评：形如A B ±的双重根式，当2A B -是一个平方数时，则能通过配方法去掉双重根号，这也是双重根号能否开方的判别技巧. 而分母有理化中，常常用到的是平方差公式，第2小题也体现了一种消去法的思想. 第（1）小题还可用平方法，即先算得原式的平方，再开方而得.第11练 §2.1.1 指数与指数幂的运算※基础达标1．化简1327()125-的结果是（ ）. A. 35 B. 53C. 3D.52．下列根式中，分数指数幂的互化，正确的是（ ）. A. 12()(0)x x x -=-> B.1263(0)y y y =< C.33441()(0)xx x-=> D.133(0)x x x -=-≠3．下列各式正确的是（ ）. A. 35351a a-= B.3322x x = C. 111111()824824a a aa-⨯⨯-⋅⋅= D. 112333142(2)12xx x x---=- 4．计算1()02(4)12(15)221--++---，结果是（ ）.A.1B. 22C. 2D. 122-5．化简111113216842(12)(12)(12)(12)(12)-----+++++，结果是（ ）.A. 11321(12)2---B. 1132(12)---C. 13212--D. 1321(12)2-- 6．化简36639494()()a a 的结果是 .7．计算2110332464()( 5.6)()0.125927--+--+= .※能力提高8．化简求值：（1）211132221566()(3)13a b a b a b -； （2）34a a a .9．已知1122x x -+=3，求下列各式的值：（1）1x x -+；（2）33222223x x x x --++++.※探究创新10．已知函数11331()()5f x x x -=-，11331()()5g x x x -=+.（1）判断()f x 、()g x 的奇偶性；（2）分别计算(4)5(2)(2)f f g -和(9)5(3)(3)f f g -，并概括出涉及函数()f x 和()g x 对所有不为0的实数x 都成立的一个等式，并加以证明.第12讲 §2.1.2 指数函数及其性质（一）¤学习目标：理解指数函数的概念和意义，能借助计算器或计算机画出具体指数函数的图像，探索并理解指数函数的单调性与特殊点，掌握指数函数的性质.¤知识要点：1. 定义：一般地，函数(0,1)x y a a a =>≠且叫做指数函数（exponential function ），其中x 是自变量，函数的定义域为R .2. 以函数2x y =与1()2x y =的图象为例，观察这一对函数的图象，可总结出如下性质：定义域为R ，值域为(0,)+∞；当0x =时，1y =，即图象过定点(0,1)；当01a <<时，在R 上是减函数，当1a >时，在R 上是增函数.¤例题精讲：【例1】求下列函数的定义域： （1）132xy -=； （2）51()3xy -=； （3）1010010100x x y +=-.解：（1）要使132xy -=有意义，其中自变量x 需满足30x -≠，即3x ≠. ∴ 其定义域为{|3}x x ≠.（2）要使51()3xy -=有意义，其中自变量x 需满足50x -≥，即5x ≤. ∴ 其定义域为{|5}x x ≤. （3）要使1010010100x x y +=-有意义，其中自变量x 需满足101000x -≠，即2x ≠. ∴其定义域为{|2}x x ≠.【例2】求下列函数的值域：（1）2311()3x y -=； （2）421x x y =++解：（1）观察易知2031x ≠-， 则有203111()()133x y -=≠=. ∴ 原函数的值域为{|0,1}y y y >≠且. （2）2421(2)21x x x x y =++=++. 令2x t =，易知0t >. 则22131()24y t t t =++=++.结合二次函数的图象，由其对称轴观察得到213()24y t =++在0t >上为增函数，所以221313()(0)12424y t =++>++=. ∴ 原函数的值域为{|1}y y >.【例3】（05年福建卷.理5文6）函数()x b f x a -=的图象如图，其中a 、b 为常数，则下列结论正确的是（ ）.A ．1,0a b ><B ．1,0a b >>C ．01,0a b <<>D ．01,0a b <<<线位置解：从曲线的变化趋势，可以得到函数()f x 为减函数，从而0<a <1；从曲b <0. 看，是由函数(01)x y a a =<<的图象向左平移|-b |个单位而得，所以-b >0，即所以选D.点评：观察图象变化趋势，得到函数的单调性，结合指数函数的单调性，得到参数a 的范围. 根据所给函数式的平移变换规律，得到参数b 的范围. 也可以取x =1时的特殊点，得到01b a a -<=，从而b <0.【例4】已知函数23()(0,1)x f x a a a -=>≠且.（1）求该函数的图象恒过的定点坐标；（2）指出该函数的单调性.解：（1）当230x -=，即23x =时，2301x a a -==. 所以，该函数的图象恒过定点2(,1)3.（2）∵ 23u x =-是减函数，∴ 当01a <<时，()f x 在R 上是增函数；当1a >时，()f x 在R 上是减函数.点评：底数两种情况的辨析，实质就是分类讨论思想的运用. 而含参指数型函数的研究，要求正确处理与参数相关的变与不变.第12练 §2.1.2 指数函数及其性质（一）※基础达标1．下列各式错误的是（ ）.A. 0.80.733>B. 0.40.60.50.5>C. 0.10.10.750.75-<D. 1.6 1.4(3)(3)> 2．已知0c <，在下列不等式中成立的是（ ）.A. 21c >B. 1()2c c >C. 12()2c c <D. 12()2c c > 3．函数y =a x +1（a ＞0且a ≠1）的图象必经过点（ ）.A.（0，1）B. （1，0）C.（2，1）D.（0，2） 4．设,a b 满足01a b <<<，下列不等式中正确的是（ ）. A. a b a a < B. a b b b < C. a a a b < D. b b b a <5．世界人口已超过56亿，若千分之一的年增长率，则两年增长的人口可相当于一个（ ）.A. 新加坡(270万)B. 香港(560万)C. 瑞士(700万)D. 上海(1200万)6．某地现有绿地100平方公里，计划每年按10%的速度扩大绿地，则三年后该地的绿地为_____平方公里.7．函数21232x x y --=的定义域为 ；函数2231()2xx y -+=的值域为 .※能力提高8．已知,a b 为不相等的正数，试比较a b a b 与b a a b 的大小.9．若已知函数23()(0,1)x f x a a a -=>≠且，()x g x a =. （1）求函数()f x 的图象恒过的定点坐标；（2）求证：1212()()()22x x g x g x g ++≤.※探究创新 10．讨论函数21(01)xy a a a +=>≠，且的值域.第13讲 §2.1.2 指数函数及其性质（二）¤学习目标：在解决简单实际问题的过程中，体会指数函数是一类重要的函数模型. 掌握指数函数的性质及应用.¤知识要点：以函数2x y =与1()2x y =的图象为例，得出这以下结论： （1）函数()y f x =的图象与()y f x =-的图象关于y 轴对称.（2）指数函数(0,1)x y a a a =>≠且的图象在第一象限内，图象由下至上，底数由下到大. ¤例题精讲：【例1】按从小到大的顺序排列下列各数：23，20.3，22，20.2.解：构造四个指数函数，分别为3x y =，0.3x y =，2x y =，0.2x y =，它们在第一象限内，图象由下至上，依次是0.2x y =，0.3x y =，2x y =，3x y =. 如右图所示.由于20x =>，所以从小到大依次排列是：20.2，20.3，22，23.点评：利用指数函数图象的分步规律，巧妙地解决了同指数的幂的大小比较问题. 当然，我们在后面的学习中，可以直接利用幂函数的单调性来比较此类大小.【例2】已知21()21x x f x -=+. （1）讨论()f x 的奇偶性； （2）讨论()f x 的单调性.解：（1）()f x 的定义域为R .∵ 21(21)21221()()21(21)21221x x x x x xx x x x f x f x ---------====-=-++++. ∴ ()f x 为奇函数.（2）设任意12,x x R ∈，且12x x <，则121212*********(22)()()2121(21)(21)x x x x x x x x f x f x ----=-=++++.由于12x x <，从而1222x x <，即12220x x -<.∴ 12()()0f x f x -<，即12()()f x f x <. ∴ ()f x 为增函数.点评：在这里，奇偶性与单调性的判别，都是直接利用知识的定义来解决. 需要我们理解两个定义，掌握其运用的基本模式，并能熟练的进行代数变形，得到理想中的结果.【例3】求下列函数的单调区间：（1）223x x y a +-=； （2）10.21x y =-.解：（1）设2,23u y a u x x ==+-.由2223(1)4u x x x =+-=+-知，u 在(,1]-∞-上为减函数，在[1,)-+∞上为增函数. 根据u y a =的单调性，当1a >时，y 关于u 为增函数；当01a <<时，y 关于u 为减函数. ∴ 当1a >时，原函数的增区间为[1,)-+∞，减区间为(,1]-∞-； 当01a <<时，原函数的增区间为(,1]-∞-，减区间为[1,)-+∞. （2）函数的定义域为{|0}x x ≠. 设1,0.21x y u u ==-. 易知0.2x u =为减函数. 而根据11y u =-的图象可以得到，在区间(,1)-∞与(1,)+∞上，y 关于u 均为减函数. ∴在(,0)-∞上，原函数为增函数；在(0,)+∞上，原函数也为增函数.点评：研究形如()(01)f x y a a a =>≠，且的函数的单调性，可以有如下结论：当1a >时，函数()f x y a =的单调性与()f x 的单调性相同；当01a <<时，函数()f x y a =的单调性与()f x 的单调性相反. 而对于形如()(01)x y a a a ϕ=>≠，且的函数单调性的研究，也需结合x a 的单调性及()t ϕ的单调性进行研究. 复合函数(())y f x ϕ=的单调性研究，遵循一般步骤和结论，即：分别求出()y f u =与()u x ϕ=两个函数的单调性，再按口诀“同增异减”得出复合后的单调性，即两个函数同为增函数或者同为减函数，则复合后结果为增函数；若两个函数一增一减，则复合后结果为减函数. 为何有“同增异减”？我们可以抓住 “x 的变化→()u x ϕ=的变化→()y f u =的变化”这样一条思路进行分析.第13练 §2.1.2 指数函数及其性质（二）※基础达标1．如果指数函数y =(2)x a -在x ∈R 上是减函数，则a 的取值范围是（ ）. A ．a ＞2 B ．a ＜3 C ．2＜a ＜3D ．a ＞32．使不等式31220x -->成立的x 的取值范围是（ ）. A. 3(,)2+∞ B. 2(,)3+∞ C. 1(,)3+∞ D.1(,)3-+∞3．某工厂去年12月份的产值是去年元月份产值的m 倍，则该厂去年产值的月平均增长率为（ ）. A. mB.12mC. 121m - D.111m -4．函数2651()()3xx f x -+=的单调递减区间为（ ）.A. (,)-∞+∞B. [3,3]-C. (,3]-∞D. [3,)+∞5．如图所示的是某池塘中的浮萍蔓延的面积(2m )与时间t (月) 的关系:t y a =,有以下叙述: ① 这个指数函数的底数是2;② 第5个月时,浮萍的面积就会超过230m ; ③ 浮萍从24m 蔓延到212m 需要经过1.5个月; ④ 浮萍每个月增加的面积都相等.其中正确的是（ ）.A. ①②③B. ①②③④C. ②③④D. ①②6．我国的人口约13亿，如果今后能将人口数年平均增长率控制在1%，那么经过x 年后我国人口数为y 亿，则y 与x 的关系式为 .7．定义运算()() ,.a ab a b b a b ≤⎧⎪*=⎨>⎪⎩ 则函数()12x f x =*的值域为 .※能力提高 8．已知(21)1()(21)1x x f x --=-+. （1）讨论()f x 的奇偶性； （2）讨论()f x 的单调性.9．求函数2233x x y -++=的定义域、值域并指出单调区间．※探究创新 10．函数23()2xax f x --=是偶函数. （1）试确定a 的值及此时的函数解析式；（2）证明函数()f x 在区间(,0)-∞上是减函数；（3）当[2,0]x ∈-时，求函数23()2xax f x --=的值域.2 1 0 y/m 2 t/月2 3814第14讲 §2.2.1 对数与对数运算（一）¤学习目标：理解对数的概念；能够说明对数与指数的关系；掌握对数式与指数式的相互转化，并能运用指对互化关系研究一些问题.¤知识要点：1. 定义：一般地，如果x a N =(0,1)a a >≠，那么数 x 叫做以a 为底 N 的对数（logarithm ）.记作 log a x N =，其中a 叫做对数的底数，N 叫做真数2. 我们通常将以10为底的对数叫做常用对数（common logarithm ），并把常用对数10log N 简记为lg N 在科学技术中常使用以无理数e=2.71828……为底的对数，以e 为底的对数叫自然对数，并把自然对数log e N 简记作ln N3. 根据对数的定义，得到对数与指数间的互化关系：当0,1a a >≠时，log b a N b a N =⇔=.4. 负数与零没有对数；log 10a =， log 1a a = ¤例题精讲：【例1】将下列指数式化为对数式，对数式化为指数式：（1）712128-=； （2）327a =； （3）1100.1-=； （4）12log 325=-； （5）lg0.0013=-； （6）ln100=4.606.解：（1）21log 7128=-； （2）3log 27a =； （3）lg 0.11=-； （4）51()322-=； （5）3100.001-=； （6） 4.606100e =. 【例2】计算下列各式的值：（1）lg 0.001； （2）4log 8； （3）ln e .解：（1）设lg 0.001x =，则100.001x =，即31010x -=，解得3x =-. 所以，lg0.0013=-.（2）设4log 8x =，则48x =，即2322x =，解得32x =. 所以，43log 82=. （3）设ln e x =，则x e e =，即12xe e =，解得12x =. 所以，1ln 2e =.【例3】求证：（1）log n a a n =； （2）log log log a a a MM N N-=.证明：（1）设log n a a x =，则n x a a =，解得x n =.所以log n a a n =.（2）设log a M p =，log a N q =，则p a M =，q a N =.因为pp q q M a a N a-==，则log log log aa a M p q M N N =-=-. 所以，log log log a a a MM N N-=.点评：对数运算性质是对数运算的灵魂，其推导以对数定义得到的指对互化关系为桥梁，结合指数运算的性质而得到. 我们需熟知各种运算性质的推导.【例4】试推导出换底公式：log log log c a c bb a=（0a >，且1a ≠；0c >，且1c ≠；0b >）. 证明：设log c b m =，log c a n =，log a b p =， 则m c b =，n c a =，p a b =. 从而()n p m c b c ==，即np m =. 由于log log 10c c n a =≠=，则m p n=.所以，log log log c a c bb a=. 点评：换底公式是解决对数运算中底数不相同时的核心工具. 其推导也密切联系指数运算性质，牢牢扣住指对互化关系.第14练 §2.2.1 对数与对数运算（一）※基础达标1．log (0,1,0)b N a b b N =>≠>对应的指数式是（ ）. A. b a N = B. a b N = C. N a b = D. N b a = 2．下列指数式与对数式互化不正确的一组是（ ）. A. 01ln10e ==与 B. 1()381118log 223-==-与 C. 123log 9293==与 D. 17log 7177==与 3．设lg 525x =，则x 的值等于（ ）.A. 10B. 0.01C. 100D. 10004．设13log 82x=，则底数x 的值等于（ ）. A. 2 B. 12 C. 4 D. 145．已知432log [log (log )]0x =，那么12x -等于（ ）.A.13 B. 123 C. 122D. 133 6．若21log 3x =，则x = ； 若log 32x =-，则x = .7．计算：3log 81= ； 6l g 0.1= . ※能力提高8．求下列各式的值：（1）22log8； （2）9log 3.9．求下列各式中x 的取值范围：（1）1log (3)x x -+； （2）12log (32)x x -+.※探究创新10．（1）设log 2a m =，log 3a n =，求2m n a +的值.（2）设{0,1,2}A =,{log 1,log 2,}a a B a =，且A B =，求a 的值.第15讲 §2.2.1 对数与对数运算（二）¤学习目标：通过阅读材料，了解对数的发现历史以及对简化运算的作用；理解对数的概念及其运算性质，知道用换底公式能将一般对数转化成自然对数或常用对数；理解推导这些运算性质的依据和过程；能较熟练地运用运算性质解决问题.¤知识要点：1. 对数的运算法则：log ()log log a a a M N M N =+，log log log aa a MM N N=-，log log n a a M n M =，其中0,1a a >≠且，0,0,M N n R >>∈. 三条法则是有力的解题工具，能化简与求值复杂的对数式.2. 对数的换底公式log log log b a b N N a =. 如果令b =N ，则得到了对数的倒数公式1log log a b b a=. 同样，也可以推导出一些对数恒等式，如log log n n a a N N =，log log m n a a nN N m=，log log log 1a b c b c a =等. ¤例题精讲：【例1】化简与求值：（1）221(lg 2)lg2lg5(lg 2)lg212++-+；（2）2log (4747)++-.解：（1）原式=2211(lg2)lg2lg5(lg 21)22++-=211lg 2lg2lg5(lg 21)42+--=2111lg 2lg2lg5lg21422+-+=1lg2(lg22lg52)14+-+=1lg2(lg1002)10114-+=+=.（2）原式=1222log (4747)⨯++-=221log (4747)2++-=221log (4747247)2++-+-=21log 142.【例2】若2510a b ==，则11a b+= . （教材P 83 B 组2题）解：由2510a b ==，得2log 10a =，5log 10b =. 则251111lg 2g5lg101log 10log 10a b +=+=+==. 【例3】 （1）方程lg lg(3)1x x ++=的解x =________；（2）设12,x x 是方程2lg lg 0x a x b ++=的两个根，则12x x 的值是 . 解：（1）由lg lg(3)1x x ++=，得lg[(3)]lg10x x +=， 即(3)10x x +=，整理为23100x x +-=. 解得x =－5或x =2. ∵ x ＞0， ∴ x =2.（2）设lg x t =，则原方程化为20t at b ++=，其两根为1122lg ,lg t x t x ==. 由121212lg lg lg()lg10b t t x x x x b +=+===，得到1210b x x =.点评：同底法是解简单对数方程的法宝，化同底的过程中需要结合对数的运算性质. 第2小题巧妙利用了换元思想和一元二次方程根与系数的关系.【例4】（1）化简：532111log 7log 7log 7++； （2）设23420052006log 3log 4log 5log 2006log 4m ⋅⋅⋅=，求实数m 的值. 解：（1）原式=77777log 5log 3log 2log (532)log 30++=⨯⨯=. （2）原式左边=2222222222log 4log 5log 2006log log 3log log 3log 4log 2005log 2006mm ⋅⋅⋅=,∴ 422log 4log 2m ==， 解得16m =.点评：换底时，一般情况下可以换为任意的底数，但习惯于化为常用对数. 换底之后，注意结合对数的运算性质完成后阶段的运算.第15练 §2.2.1 对数与对数运算（二）※基础达标 1．1logn n++（1n n ＋－）等于（ ）. A. 1B. －1C. 2D. －2 2．25log ()(5)a -（a ≠0）化简得结果是（ ）.A. －aB. a 2C. ｜a ｜D. a3．化简3lg 2lg 5log 1++的结果是（ ）.A.12B. 1C. 2D.10 4．已知32()log f x x =, 则(8)f 的值等于（ ）.A. 1B. 2C. 8D. 125．化简3458log 4log 5log 8log 9⋅⋅⋅的结果是 （ ）.A .1 B.32C. 2D.3 6．计算2(lg5)lg 2lg50+⋅＝ .7．若3a ＝2，则log 38－2log 36＝ . ※能力提高8．（1）已知18log 9a =，185b =，试用a 、b 表示18log 45的值；（2）已知1414log 7log 5a b ==，，用a 、b 表示35log 28.9．在不考虑空气阻力的条件下，火箭的最大速度(/)v m s 和燃料的质量()M kg 、火箭（除燃料外）的质量()m kg 的关系是2000ln(1)Mv m=+. 当燃料质量是火箭质量的多少倍时，火箭的最大速度可达到10/km s ？※探究创新10．（1）设,,x y z 均为实数，且34x y =，试比较3x 与4y 的大小.（2）若a 、b 、c 都是正数，且至少有一个不为1，1x y z y z x z x y a b c a b c a b c ===，讨论x 、y 、z 所满足的关系式.第16讲 §2.2.2 对数函数及其性质（一）¤学习目标：通过具体实例，直观了解对数函数模型所刻画的数量关系，初步理解对数函数的概念，体会对数函数是一类重要的函数模型；能借助计算器或计算机画出具体对数函数的图像，探索并了解对数函数的单调性与特殊点.¤知识要点：1. 定义：一般地，当a ＞0且a ≠1时，函数a y=log x 叫做对数函数(logarithmic function). 自变量是x ； 函数的定义域是（0，+∞）.2. 由2log y x =与12log y x =的图象，可以归纳出对数函数的性质：定义域为(0,)+∞，值域为R ；当1x =时，0y =，即图象过定点(1,0)；当01a <<时，在(0,)+∞上递减，当1a >时，在(0,)+∞上递增.¤例题精讲：【例1】比较大小：（1）0.9log 0.8，0.9log 0.7，0.8log 0.9； （2）3log 2，2log 3，41log 3. 解：（1）∵ 0.9log y x =在(0,)+∞上是减函数，且0.90.80.7>>， ∴ 0.90.91log 0.8log 0.7<<.又 0.80.8log 0.9log 0.81<=， 所以0.80.90.9log 0.9log 0.8log 0.7<<. （2）由 333log 1log 2log 3<<，得30log 21<<. 又22log 3log 21>=，441log log 103<=， 所以4321log log 2log 33<<. 【例2】求下列函数的定义域：（1）2log (35)y x =-；（2）0.5log (4)3y x =-. 解：（1）由22log (35)0log 1x -≥=，得351x -≥，解得2x ≥. 所以原函数的定义域为[2,)+∞.（2）由0.5log (4)30x -≥，即30.50.5log (4)3log 0.5x ≥=，所以3040.5x <≤，解得1032x <≤. 所以，原函数的定义域为1(0,]32. 【例3】已知函数()log (3)a f x x =+的区间[2,1]--上总有|()|2f x <，求实数a 的取值范围. 解：∵ [2,1]x ∈--， ∴ 132x ≤+≤当1a >时，log 1log (3)log 2a a a x ≤+≤，即0()log 2a f x ≤≤. ∵ |()|2f x <， ∴{1log 22a a ><， 解得2a >.当01a <<时，log 2log (3)log 1a a a x ≤+≤，即log 2()0a f x ≤≤. ∵ |()|2f x <， ∴{01log 22a a <<>-， 解得202a <<.综上可得，实数a 的取值范围是2(0,)(2,)2+∞. 点评：先对底数a 分两种情况讨论，再利用函数的单调性及已知条件，列出关于参数a 的不等式组，解不等式（组）而得到参数的范围. 解决此类问题的关键是合理转化与分类讨论，不等式法求参数范围.【例4】求不等式log (27)log (41)(0,1)a a x x a a +>->≠且中x 的取值范围.解：当1a >时，原不等式化为2704102741x x x x +>⎧⎪->⎨+>-⎪⎩，解得144x <<.当01a <<时，原不等式化为 2704102741x x x x +>⎧⎪->⎨+<-⎪⎩，解得4x >.所以，当1a >时，x 的取值范围为1(,4)4；当01a <<时，x 的取值范围为(4,)+∞.点评：结合单调性，将对数不等式转化为熟悉的不等式组，注意对数式有意义时真数大于0的要求. 当底数a 不确定时，需要对底数a 分两种情况进行讨论.第16练 §2.2.2 对数函数及其性质（一）※基础达标1．下列各式错误的是（ ）.A. 0.80.733>B. 0.10.10.750.75-<C. 0..50..5log 0.4log 0.6>D. lg1.6lg1.4>.2．当01a <<时,在同一坐标系中,函数log x a y a y x -==与的图象是（ ）.A B C D 3．下列函数中哪个与函数y =x 是同一个函数（ ）A.log (0,1)a xy a a a =>≠ B. y =2x xC. log (0,1)x a y a a a =>≠D. y =2x4．函数12log (1)y x =-的定义域是（ ）.A. (1,)+∞B. (,2)-∞C. (2,)+∞D. (1,2] 5．若log 9log 90m n <<，那么,m n 满足的条件是（ ）.A. 1 m n >>B. 1n m >>C. 01n m <<<D. 01m n <<< 6．函数3log y x =的定义域为 . （用区间表示）7．比较两个对数值的大小：ln 7 ln12 ； 0.5log 0.7 0.5log 0.8. ※能力提高8．求下列函数的定义域：（1） ()()34log 11xf x x x -=++-； （2）21log (45)y x =--.9．已知函数2()3log ,[1,4]f x x x =+∈，22()()[()]g x f x f x =-，求： （1）()f x 的值域； （2）()g x 的最大值及相应x 的值.※探究创新10．若,a b 为不等于1的正数，且a b <，试比较log a b 、1log a b 、1log b b.第17讲 §2.2.2 对数函数及其性质（二）¤学习目标：掌握对数函数的性质，并能应用对数函数解决实际中的问题. 知道指数函数y =a x 与对数函数y =log ax 互为反函数. （a > 0, a ≠1）¤知识要点：1. 当一个函数是一一映射时, 可以把这个函数的因变量作为一个新函数的自变量, 而把这个函数的自变量新的函数的因变量. 我们称这两个函数为反函数（inverse function ）. 互为反函数的两个函数的图象关于直线y x =对称.xy1 1oxy o 1 1oy x11 oy x1 12. 函数(0,1)x y a a a =>≠与对数函数log (0,1)a y x a a =>≠互为反函数.3. 复合函数(())y f x ϕ=的单调性研究，口诀是“同增异减”，即两个函数同增或同减，复合后结果为增函数；若两个函数一增一减，则复合后结果为减函数. 研究复合函数单调性的具体步骤是：（i ）求定义域；（ii ）拆分函数；（iii ）分别求(),()y f u u x ϕ==的单调性；（iv ）按“同增异减”得出复合函数的单调性.¤例题精讲：【例1】讨论函数0.3log (32)y x =-的单调性.解：先求定义域，由320x ->, 解得32x <. 设332,(,)2t x x =-∈-∞，易知为减函数. 又∵ 函数0.3log y t =是减函数，故函数0.3log (32)y x =-在3(,)2-∞上单调递增.【例2】（05年山东卷.文2）下列大小关系正确的是（ ）. A. 30.440.43log 0.3<< B. 30.440.4log 0.33<< C. 30.44log 0.30.43<< D. 0.434log 0.330.4<<变量x解：在同一坐标系中分别画出40.4,3,log x x y y y x ===的图象，分别作出当自取3，0.4，0.3时的函数值.观察图象容易得到：30.44log 0.30.43<<. 故选C.【例3】指数函数(0,1)x y a a a =>≠的图象与对数函数log (0,1)a y x a a =>≠的图象有何关系？ 解：在指数函数x y a =的图象上任取一点00(,)M x y ，则00x y a =. 由指对互化关系，有00log a y x =.所以，点00'(,)M y x 在对数函数log a y x =的图象上. 因为点00(,)M x y 与点00'(,)M y x 关于直线y x =对称，所以指数函数(0,1)x y a a a =>≠的图象与对数函数log (0,1)a y x a a =>≠的图象关于直线y x =对称. 点评：两个函数的对称性，由任意点的对称而推证出来. 这种对称性实质是反函数的图象特征，即函数x y a =与log (0,1)a y x a a =>≠互为反函数，而互为反函数的两个函数图象关于直线y x =对称.【例4】2005年10月12日，我国成功发射了“神州”六号载人飞船，这标志着中国人民又迈出了具有历史意义的一步.已知火箭的起飞重量M 是箭体（包括搭载的飞行器）的重量m 和燃料重量x 之和.在不考虑空气阻力的条件下，假设火箭的最大速度y 关于x 的函数关系式为：[ln()ln(2)]4ln 2(0)y k m x m k =+-+≠其中. 当燃料重量为(1)e m -吨（e 为自然对数的底数， 2.72e ≈）时，该火箭的最大速度为4（km/s ）.（1）求火箭的最大速度(/)y km s 与燃料重量x 吨之间的函数关系式()y f x =；（2）已知该火箭的起飞重量是544吨，是应装载多少吨燃料，才能使该火箭的最大飞行速度达到8km/s ，顺利地把飞船发送到预定的轨道？解：（1）依题意把(1),4x e m y =-=代入函数关系式[ln()ln(2)]4ln 2y k m x m =+-+，解得8k =. 所以所求的函数关系式为8[ln()ln(2)]4ln 2,y m x m =+-+ 整理得8ln().m x y m+= （2）设应装载x 吨燃料方能满足题意，此时，544,8m x y =-= 代入函数关系式8544ln(),ln 1,344().544m x y x m x+===-得解得吨 所以，应装载344吨燃料方能顺利地把飞船发送到预定的轨道.点评：直接给定参数待定的函数模型时，由待定系数法的思想，代入已知的数据得到相关的方程而求得待定系数. 一般求出函数模型后，还利用模型来研究一些其它问题. 代入法、方程思想、对数运算，是解答此类问题的方法精髓.第17练 §2.2.2 对数函数及其性质（二）※基础达标 1．函数1lg1xy x+=－的图象关于（ ）. A. y 轴对称B. x 轴对称C. 原点对称D. 直线y ＝x 对称2．函数212log (617)y x x =-+的值域是（ ）.A. RB. [8,)+∞C. (,3]-∞-D. [3,)+∞3．（07年全国卷.文理8）设1a >，函数()log a f x x =在区间[]2a a ，上的最大值与最小值之差为12，则a =（ ）. A.2B. 2C. 22D. 44．图中的曲线是log a y x =的图象，已知a 的值为2，43，310，15，则相应曲线1234,,,C C C C 的a 依次为（ ）.A.2，43，15，310 B. 2，43，310，15 C. 15，310，43，2 D. 43，2，310，155．下列函数中，在(0,2)上为增函数的是（ ）.A. 12log (1)y x =+ B. 22log 1y x =- C. 21log y x= D.20.2log (4)y x =-6． 函数2()lg(1)f x x x =+-是 函数. （填“奇”、“偶”或“非奇非偶”） 7．函数x y a =的反函数的图象过点(9,2)，则a 的值为 . ※能力提高 8．已知6()log ,(0,1)a f x a a x b=>≠-，讨论()f x 的单调性.9．我们知道，人们对声音有不同的感觉，这与它的强度有关系. 声音的强度I 用瓦/平方米 （2/W m ）表示. 但在实际测量中，常用声音的强度水平1L 表示，它们满足以下公式：1010lg IL I = （单位为分贝），10L ≥，其中120110I -=⨯，这是人们平均能听到的最小强度，是听觉的开端. 回答以下问题：（1）树叶沙沙声的强度是122110/W m -⨯，耳语的强度是102110/W m -⨯，恬静的无限电广播的强度为82110/W m -⨯. 试分别求出它们的强度水平. （2）在某一新建的安静小区规定：小区内的公共场所声音的强度水平必须保持在50分贝以下，试求声音强度I 的范围为多少？※探究创新10． 已知函数()log (1),()log (1)a a f x x g x x =+=-其中(01)a a >≠且．（1）求函数()()f x g x -的定义域； （2）判断()()f x g x -的奇偶性，并说明理由；（3）求使()()0f x g x ->成立的x 的集合.第18讲 §2.3 幂函数¤学习目标：通过实例，了解幂函数的概念；结合函数y=x, y=x 2, y=x 3, y =1/x , y=x 1/2 的图像，了解它们的变化情况.知识要点：1. 幂函数的基本形式是y x α=，其中x 是自变量，α是常数. 要求掌握y x =，2y x =，3y x =，1/2y x =，1y x -=这五个常用幂函数的图象.2. 观察出幂函数的共性，总结如下：（1）当0α>时，图象过定点(0,0),(1,1)；在(0,)+∞上是增函数.（2）当0α<时，图象过定点(1,1)；在(0,)+∞上是减函数；0 x C 1C 2C 4C 3 1y在第一象限内，图象向上及向右都与坐标轴无限趋近.3. 幂函数y x α=的图象，在第一象限内，直线1x =的右侧，图象由下至上，指数α由小到大. y 轴和直线1x =之间，图象由上至下，指数α由小到大.¤例题精讲：【例1】已知幂函数()y f x =的图象过点(27,3)，试讨论其单调性. 解：设y x α=，代入点(27,3)，得327α=，解得13α=， 所以13y x =，在R 上单调递增.【例2】已知幂函数6()m y x m Z -=∈与2()m y x m Z -=∈的图象都与x 、y 轴都没有公共点，且2()m y x m Z -=∈的图象关于y 轴对称，求m 的值．解：∵ 幂函数图象与x 、y 轴都没有公共点，∴{6020m m -<-<，解得26m <<.又 ∵ 2()m y x m Z -=∈的图象关于y 轴对称， ∴ 2m -为偶数，即得4m =. 【例3】幂函数m y x =与n y x =在第一象限内的图象如图所示，则（ ）. A ．101n m -<<<< B ．1,01n m <-<<C ．10,1n m -<<>D ．1,1n m <->解：由幂函数图象在第一象限内的分布规律，观察第一象限内直线1x =的右侧，图象由下至上，依次是n y x =，1y x -=，0y x =，m y x =，1y x =，所以有101n m <-<<<. 选B.点评：观察第一象限内直线1x =的右侧，结合所记忆的分布规律. 注意比较两个隐含的图象1y x =与0y x =.【例4】本市某区大力开展民心工程，近几年来对全区2a m 的老房子进行平改坡（“平改坡”是指在建筑结构许可条件下，将多层住宅平屋面改建成坡屋顶，并对外墙面进行整修粉饰，达到改善住宅性能和建筑物外观视觉效果的房屋修缮行为），且每年平改坡面积的百分比相等. 若改造到面积的一半时，所用时间需10年. 已知到今年为止，平改坡剩余面积为原来的22. （1）求每年平改坡的百分比；（2）问到今年为止，该平改坡工程已进行了多少年？ （3）若通过技术创新，至少保留24a m 的老房子开辟新的改造途径. 今后最多还需平改坡多少年？ 解：（1）设每年平改坡的百分比为(01)x x <<，则101(1)2a x a -=，即11011()2x -=，解得11011()0.0670 6.702x =-≈=%.（2）设到今年为止，该工程已经进行了n 年，则2(1)2na x a -=，即110211()()22n=，解得n =5. 所以，到今年为止，该工程已经进行了5年. （3）设今后最多还需平改坡m 年，则 51(1)4m a x a +-=，即521011()()22m +=，解得m =15. 所以，今后最多还需平改坡15年.点评：以房屋改造为背景，从中抽象出函数模型，结合两组改造数据及要求，通过三个等式求得具有实际意义的底数或指数. 体现了代入法、方程思想等数学方法的运用.第18练 §2.3 幂函数※基础达标1．如果幂函数()f x x α=的图象经过点2(2,)2，则(4)f 的值等于（ ）. A. 16 B. 2 C. 116 D. 122．下列函数在区间(0,3)上是增函数的是（ ）.A. 1y x =B. 12y x = C. 1()3x y = D. 2215y x x =--3．设120.7a =，120.8b =，c 3log 0.7=，则（ ）.A. c <b <aB. c <a <bC. a <b <cD. b <a <c4．如图的曲线是幂函数n y x =在第一象限内的图象. 已知n 分别取2±，12±四个值，与曲线1c 、2c 、3c 、4c 相应的n 依次为（ ）.A ．112,,,222-- B. 112,,2,22--C. 11,2,2,22--D. 112,,,222--5．下列幂函数中过点(0,0)，(1,1)的偶函数是（ ）. A.12y x = B. 4y x = C. 2y x -= D.13y x =6．幂函数()y f x =的图象过点1(4,)2，则(8)f 的值为 .7．比较下列各组数的大小： 32(2)a + 32a ； 223(5)a -+ 235-； 0.50.4 0.40.5.※能力提高8．幂函数273235()(1)t t f x t t x +-=-+是偶函数，且在(0,)+∞上为增函数，求函数解析式.9．1992年底世界人口达到54.8亿，若人口的平均增长率为x %，2008年底世界人口数为y （亿）.（1）写出1993年底、1994年底、2000年底的世界人口数； （2）求2008年底的世界人口数y 与x 的函数解析式. 如果要使2008年的人口数不超过66.8亿，试求人口的年平均增长率应控制在多少以内？※探究创新10．请把相应的幂函数图象代号填入表格.① 23y x =； ② 2y x -=；③ 12y x =； ④ 1y x -=； ⑤ 13y x =；⑥ 43y x =；⑦ 12y x-=；⑧ 53y x =.第19讲 第二章 基本初等函数（Ⅰ） 复习¤学习目标：理解掌握指数函数、对数函数和幂函数的性质、图象及运算性质. 突出联系与转化、分类与讨论、数与形结合等重要的数学思想、能力. 通过对指数函数、对数函数等具体函数的研究，加深对函数概念的理解.¤例题精讲：【例1】若()(0,1)x f x a a a =>≠且，则1212()()()22x x f x f x f ++≤. 证明：121212122()()()222x x x x f x f x x x a a f a ++++-=-12121222()022x x x x x x a a a a a a +--==≥. ∴ 1212()()()22x x f x f x f ++≤. （注：此性质为函数的凹凸性） 函数代号 ① ② ③ ④ ⑤ ⑥ ⑦ ⑧ 图象代号42-2510c 4c 3c 2c 1【例2】已知函数2()(0,0)1bxf x b a ax =≠>+. （1）判断()f x 的奇偶性； （2）若3211(1),log (4)log 422f a b =-=，求a ，b 的值.解：（1）()f x 定义域为R ，2()()1bxf x f x ax --==-+，故()f x 是奇函数.（2）由1(1)12b f a ==+，则210a b -+=.又log 3(4a -b )=1，即4a -b =3.由{21043a b a b -+=-=得a =1，b =1.【例3】（01天津卷.19）设a ＞0， ()x x e af x a e=+是R 上的偶函数.（1）求a 的值； （2）证明()f x 在(0,)+∞上是增函数．解：（1）∵ ()x x e af x a e=+是R 上的偶函数，∴ ()()0f x f x --=.∴ 110()()x x x x x x e a e a a e a e a e a e a a---+--=⇒-+-10()()0x x a e e a -=⇒--=.e x －e -x 不可能恒为“0”， ∴ 当1a－a ＝0时等式恒成立， ∴a ＝1．（2）在(0,)+∞上任取x 1＜x 2，1212121212111()()()()x x x x x x x x e f x f x e e e a e e e e -=+--=-+-12121()(1)x x x x e e e e =--∵ e ＞1，x 1＜x 2， ∴ 121x x e e >>， ∴12x x e e ＞1，121212()(1)x x x x x x e e e e e e --＜0，∴ 12()()0f x f x -<， ∴ ()f x 是在(0,)+∞上的增函数．点评：本题主要考查了函数的奇偶性以及单调性的基础知识．此题中的函数，也可以看成指数函数x y a =与x a y a x =+的复合，可以进一步变式探讨x ay a x=+的单调性. 【例4】已知1992年底世界人口达到54.8亿.（1）若人口的平均增长率为1.2%，写出经过t 年后的世界人口数y （亿）与t 的函数解析式；（2）若人口的平均增长率为x %，写出2010年底世界人口数为y （亿）与x 的函数解析式. 如果要使2010年的人口数不超过66.8亿，试求人口的年平均增长率应控制在多少以内？ 解：（1）经过t 年后的世界人口数为 *54.8(1 1.2)54.8 1.012,t t y t N =⨯+%=⨯∈. （2）2010年底的世界人口数y 与x 的函数解析式为 1854.8(1)y x =⨯+%. 由1854.8(1)y x =⨯+%≤66.8， 解得1866.8100(1) 1.154.8x ≤⨯-≈. 所以，人口的年平均增长率应控制在1.1%以内.点评：解应用题应先建立数学模型，再用数学知识解决，然后回到实际问题，给出答案. 此题由增长率的知识，可以得到指数型或幂型函数，并得到关于增长率的简单不等式，解决实际中增长率控制问题.第19练 第二章 基本初等函数（Ⅰ） 复习※基础达标1．（06年全国卷II.文2理1）已知集合{}2{|3},|log 1M x x N x x =<=>，则M N =（ ）.A. ∅B. {}|03x x <<C. {}|13x x <<D. {}|23x x << 2．（08年北京卷.文2）若372log πlog 6log 0.8a b c ===，，，则（ ）. A. a b c >> B. b a c >> C. c a b >> D. b c a >>3.（05年福建卷）函数()x b f x a -=的图象如图，其中a 、b 为常数，则下列结论正确的是（ ）. A. 1,0a b >< B. 1,0a b >>C. 01,0a b <<>D. 01,0a b <<<。

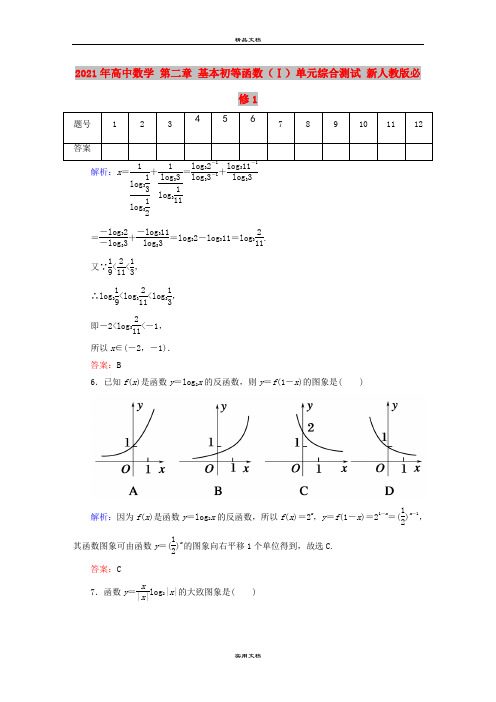
2021年高中数学 第二章 基本初等函数（Ⅰ）单元综合测试 新人教版必修1题号 1 23 4567 8 9 10 11 12 答案解析：x ＝log 313log 312＋log 33log 3111＝3log 33－1＋3log 33 ＝－log 32－log 33＋－log 311log 33＝log 32－log 311＝log 3211.又∵19<211<13，∴log 319<log 3211<log 313，即－2<log 3211<－1，所以x ∈(－2，－1)． 答案：B6．已知f (x )是函数y ＝log 2x 的反函数，则y ＝f (1－x )的图象是( )解析：因为f (x )是函数y ＝log 2x 的反函数，所以f (x )＝2x，y ＝f (1－x )＝21－x＝(12)x －1，其函数图象可由函数y ＝(12)x的图象向右平移1个单位得到，故选C.答案：C7．函数y ＝x|x |log 2|x |的大致图象是( )解析：当x >0时，y ＝x xlog 2x ＝log 2x ， 当x <0时，y ＝x－x log 2(－x )＝－log 2(－x )，分别作图象可知选D. 答案：D 8．函数y ＝lg ⎝⎛⎭⎪⎫21－x －1的图象关于( )A ．y 轴对称B ．x 轴对称C ．原点对称D ．直线y ＝x 对称解析：y ＝lg ⎝ ⎛⎭⎪⎫21－x －1＝lg 1＋x 1－x ，故原函数为奇函数，因此图象关于原点对称．答案：C9．已知a ＝log 23＋log 23，b ＝log 29－log 23，c ＝log 32，则a ，b ，c 的大小关系是( ) A ．a ＝b <c B ．a ＝b >c C ．a <b <cD ．a >b >c解析：∵a ＝log 23＋log 23＝log 233，b ＝log 29－log 23＝log 233，∴a ＝b . 又函数y ＝log a x (a >1)为增函数，∴a ＝log 233>log 22＝1，c ＝log 32<log 33＝1， ∴a ＝b >c . 答案：B10．如果一个点是一个指数函数与一个对数函数的图象的公共点，那么称这个点为“好点”．在下面的五个点M (1,1)，N (1,2)，P (2,1)，Q (2,2)，G ⎝ ⎛⎭⎪⎫2，12中，可以是“好点”的个数为( )A ．0B ．1C ．2D ．3解析：设指数函数y ＝a x(a >0，且a ≠1)，则可知N ，Q ，G 可以满足指数函数的条件．设对数函数y ＝log a x (a >0，且a ≠1)，则可知P ，Q ，G 可以满足对数函数的条件，故“好点”为Q ，G ，共2个．答案：C11．函数f (x )＝a x＋log a (x ＋1)在[0,1]上的最大值与最小值和为a ，则a 的值为( ) A.14 B.12 C ．2D ．4解析：∵函数y ＝a x 与y ＝log a (x ＋1)在[0,1]上具有相同的单调性，∴函数f (x )的最大值、最小值应在[0,1]的端点处取得，由a 0＋log a 1＋a 1＋log a 2＝a ，得a ＝12.答案：B12．设f (x )是定义在(－∞，＋∞)上的偶函数，且它在[0，＋∞)上单调递增，若，则a ，b ，c 的大小关系是( )A ．a >b >cB ．b >c >aC ．c >a >bD ．c >b >a答案：C第Ⅱ卷(非选择题，共90分)二、填空题(每小题5分，共20分)13．已知函数f (x )＝lg x ，若f (ab )＝1，则f (a 2)＋f (b 2)＝________. 解析：由f (ab )＝1，得lg(ab )＝1，于是f (a 2)＋f (b 2)＝lg a 2＋lg b 2＝2lg(ab )＝2. 答案：214．若函数f (x )＝(3－a )x与g (x )＝log a x 的增减性相同，则实数a 的取值范围是________．解析：由题意得⎩⎪⎨⎪⎧0<3－a <1，0<a <1或⎩⎪⎨⎪⎧3－a >1，a >1，所以1<a <2.所以实数a 的取值范围是(1,2)． 答案：(1,2)15．如图，矩形ABCD 的三个顶点A ，B ，C 分别在函数y ＝，y ＝x12 ，y ＝(22)x的图象上，且矩形的边分别平行于两坐标轴．若点A 的纵坐标为2，则点D 的坐标为________．解析：由图象可知，点A (x A,2)在函数y ＝log 22x 的图象上， 所以2＝A ，x A ＝(22)2＝12.点C (4，y C )在函数y ＝(22)x的图象上， 所以y C ＝(22)4＝14. 又x D ＝x A ＝12，y D ＝y C ＝14，所以点D 的坐标为(12，14)．答案：(12，14)16．已知函数f (x )＝e |x －a |(a 为常数)．若f (x )在区间[1，＋∞)上是增函数，则a 的取值范围是________．解析：∵g (x )＝|x －a |的增区间为[a ，＋∞)， ∴f (x )＝e|x －a |的增区间为[a ，＋∞)．∵f (x )在[1，＋∞)上是增函数， ∴[1，＋∞)⊆[a ，＋∞)． ∴a ≤1，即a ∈(－∞，1]． 答案：(－∞，1]三、解答题(写出必要的计算步骤，只写最后结果不得分，共70分) 17．(10分)求值：解：(1)原式＝1＋14×25－32＝－25.(2)原式＝(lg2lg3＋lg22lg3)·(lg32lg2＋lg33lg2)＋14＋12－0＝3lg22lg3·5lg36lg2＋34＝54＋34＝2. 18．(12分)已知函数f (x )＝log 3(ax ＋b )的图象经过点A (2,1)，B (5,2)． (1)求函数f (x )的解析式及定义域． (2)求f (14)÷f (3＋12)的值． 解：(1)∵函数f (x )＝log 3(ax ＋b )的图象经过点A (2,1)，B (5,2)，∴⎩⎪⎨⎪⎧f2＝1，f 5＝2，即⎩⎪⎨⎪⎧log 32a ＋b ＝1，log 35a ＋b ＝2，∴⎩⎪⎨⎪⎧2a ＋b ＝3，5a ＋b ＝9，解得⎩⎪⎨⎪⎧a ＝2，b ＝－1，∴f (x )＝log 3(2x －1)，定义域为(12，＋∞)．(2)f (14)÷f (3＋12)＝log 327÷log 33＝3÷12＝6. 19．(12分)已知a >0，且a ≠1，若函数f (x )＝2a x－5在区间[－1,2]的最大值为10，求a 的值．解：当0<a <1时，f (x )在[－1,2]上是减函数，当x ＝－1时，函数f (x )取得最大值，则由2a －1－5＝10，得a ＝215，当a >1时，f (x )在[－1,2]上是增函数， 当x ＝2时，函数取得最大值，则由2a 2－5＝10， 得，a ＝302或a ＝－302(舍)， 综上所述，a ＝215或302.20．(12分)已知x ∈[－3,2]，求f (x )＝14x －12x ＋1的最小值与最大值．解：设12x ＝t ，即(12)x＝t ，∵x ∈[－3,2]，∴14≤t ≤8.∴f (t )＝t 2－t ＋1＝(t －12)2＋34.又∵14≤t ≤8，∴当t ＝12，即x ＝1时， f (x )有最小值34；当t ＝8，即x ＝－3时， f (x )有最大值57.21．(12分)已知y ＝f (x )是定义在R 上的奇函数，且x <0时，f (x )＝1＋2x. (1)求函数f (x )的解析式． (2)画出函数f (x )的图象． (3)写出函数f (x )单调区间及值域．解：(1)因为y ＝f (x )是定义在R 上的奇函数， 所以f (－0)＝－f (0)，所以f (0)＝0， 因为x <0时，f (x )＝1＋2x， 所以x >0时，f (x )＝－f (－x )＝－(1＋2－x)＝－1－12x ，所以f (x )＝⎩⎪⎨⎪⎧1＋2x，x <0，0，x ＝0，－1－12x，x >0.(2)函数f (x )的图象为(3)根据f (x )的图象知：f (x )的单调增区间为(－∞，0)，(0，＋∞)；值域为{y |1<y <2或－2<y <－1或y ＝0}．22．(12分)设f (x )＝log 12 (10－ax )，a 为常数．若f (3)＝－2.(1)求a 的值；(2)求使f (x )≥0的x 的取值范围；(3)若对于区间[3,4]上的每一个x 的值，不等式f (x )>(12)x＋m 恒成立，求实数m 的取值范围．解：(1)∵f (3)＝－2， ∴log 12 (10－3a )＝－2.即10－3a ＝(12)－2，∴a ＝2.(2)∵f (x )＝log 12 (10－2x )≥0，∴10－2x ≤1.又10－2x >0，∴x ∈[92，5)．(3)设g (x )＝log 12 (10－2x )－(12)x.由题意知g (x )>m 在x ∈[3,4]上恒成立，∵g (x )在[3,4]上为增函数，∴m <g (3)＝－178.25617 6411 搑33038 810E 脎/=n2 %35271 89C7 觇23916 5D6C 嵬J36779 8FAB 辫z353558A1B 訛n。

2019-2020学年必修1第二章训练卷基本初等函数（一）注意事项：1．答题前，先将自己的姓名、准考证号填写在试题卷和答题卡上，并将准考证号条形码粘贴在答题卡上的指定位置。

2．选择题的作答：每小题选出答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑，写在试题卷、草稿纸和答题卡上的非答题区域均无效。

3．非选择题的作答：用签字笔直接答在答题卡上对应的答题区域内。

写在试题卷、草稿纸和答题卡上的非答题区域均无效。

4．考试结束后，请将本试题卷和答题卡一并上交。

一、选择题(本大题共12个小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的) 1．下列函数不是幂函数的是（ ） A ．3y x =B ．2y x =C ．3xy =D ．12y x-=【答案】C【解析】幂函数是形如ay x =形式的函数，选项C 为指数函数，故选C ．2．若0m >，0n >，0a >且1a ≠，则下列等式正确的是（ ） A ．nnaa -=B ．log log log ()a a a m n m n ⋅=+C ．3322m m =D ．()mmm a a bb=【答案】D 【解析】1nn aa-=，故A 错误； log log log ()a a a m n mn +=，故B 错误；2323m m =，故C 错误；应选D ．3．函数log (21)3a y x =-+的图象必过点（ ） A ．1(,4)2B ．(1,3)C ．1(,3)2D ．(1,4)【答案】B【解析】当1x =时，211x -=，则log 13033a y =+=+=， ∴函数log (21)3a y x =-+的图象必过点(1,3)，应选B ． 4．计算25log 25log 16⋅=（ ） A ．8 B ．10 C ．16 D ．40【答案】A【解析】24252525log 25log 16log 5log 22log 54log 28⋅=⋅=⨯=，应选A ．5．下列函数中，在区间(0,)+∞上为减函数的是（ ）A ．2y x =B ．12y x =C ．2xy -=D ．ln y x =【答案】C【解析】选项A 、B 、D 在区间(0,)+∞均为增函数，选项C 在区间(0,)+∞上为减函数，故选C ．6．函数()ln(1)21f x x x =-+-的定义域为（ ） A ．1(,1)2B ．1[,1)2C ．1(,1]2D ．1[,1]2【答案】B【解析】由题意可知10210x x ->⎧⎨-≥⎩，解得112x ≤<，故选B ．7．已知幂函数()y f x =经过2(4,)2，则(16)f =（ ） 此卷只装订不密封班级 姓名 准考证号 考场号 座位号A ．2B ．12C ．14D ．4【答案】B【解析】设()af x x =，∵()y f x =经过2(4,)2，则242a =，得14a =-， ∴14()f x x-=，∴141(16)162f -==，故选B ． 8．三个数0.87，70.8，0.8log 7的大小顺序是（ ）A ．70.80.8log 70.87<<B ．0.870.8log 770.8<<C ．70.80.80.87log 7<< D ．0.870.870.8log 7<<【答案】A 【解析】0.871>，700.81<<，0.8log 70<，故70.80.8log 70.87<<，故选A ．9．10025a=，108b=，则3a b +=（ ） A ．12B ．13C ．2D ．3【答案】D【解析】∵10025a=，∴100log 25lg 5a ==，又∵108b=，∴lg83lg 2b ==，∴33lg53lg 23lg103a b +=+==，故选D ． 10．已知函数①ay x =，②by x =，③cy x =，④dy x =的部分图象如下图，则下列正确的是（ ）A ．a b c d <<<B ．c a d b <<<C ．c b d a <<<D ．c d b a <<<【答案】C【解析】由图可知0c <，1d =，01b <<，1a >，故c b d a <<<．应选C ． 11．若对数函数()log a f x x =的图象与函数()y g x =的图象关于y x =对称，且当0x <时()1g x >，则a 的取值范围是（ ）A ．01a <<B ．0a >且1a ≠C ．1a >D ．12a <<【答案】A【解析】由题意可知，()xg x a =，当0x <时，()1g x >，可知01a <<，故选A ．12．已知log (83)a y ax =-（0a >且1a ≠）在[0,2]上是x 的减函数，则a 的取值范围是（ ） A ．(0,1) B ．3(,1)4C ．8(1,)3D ．4(1,)3【答案】D【解析】令83t ax =-，则log a y t =，当01a <<时，log a y t =单减，而83t ax =-也是减函数， 故log (83)a y ax =-是关于x 的增函数，不合题意，舍去；当1a >时，log a y t =单增，83t ax =-单减， 故符合log (83)a y ax =-是关于x 的减函数． ∵[0,2]x ∈，∴[86,8]t a ∈-，∴860a ->得43a <，则413a <<．应选D ．二、填空题（本大题共4个小题，每小题5分，共20分，把正确答案填在题中横线上）13．计算：8527log 27log 16log 625⨯⨯= ．【答案】163【解析】3448527253log 27log 16log 625log 3log 2log 5⨯⨯=⨯⨯2531616lg 3lg 2lg 516log 3log 2log 533lg 2lg 5lg 33=⨯⨯=⨯⨯⨯=． 14．已知函数()2log ,(0)3,(0)xx x f x x ->⎧=⎨≤⎩，则1()2f f ⎡⎤=⎢⎥⎣⎦．【答案】3【解析】211()log 122f ==-，1(1)33f -==，∴1()(1)32f f f ⎡⎤=-=⎢⎥⎣⎦， 故答案为3．15．函数21()(5)m f x m m x +=--是幂函数，且为奇函数，则实数m 的值是 ．【答案】2-【解析】∵()f x 是幂函数，∴251m m --=，∴260m m --=， 解得2m =-或3，当2m =-时，11m +=-，1()f x x -=是奇函数，符合题意； 当3m =时，14m +=，4()f x x =是偶函数，不符合题意，∴2m =-．16．若函数()log (01)a f x x a =<<在区间1,22a a ⎡⎤⎢⎥⎣⎦上的最大值是最小值的2倍，则a = ． 【答案】18【解析】∵01a <<，∴()log a f x x =在区间1,22a a ⎡⎤⎢⎥⎣⎦上是单调递减函数，∴max 111()()log ()log 1222a af x f a a ===+，min ()(2)log (2)log 21a a f x f a a ===+，max min ()2()f x f x =，∴1log 12(log 21)2a a +=+，得1log 2log 212a a -=， 即1log 18a =，解得18a =．三、解答题(本大题共6个大题，共70分，解答应写出文字说明，证明过程或演算步骤)17．（10分）已知函数2()log ()f x mx n =+，若(3)1f =-，(10)2f =，求(4)f ． 【答案】0．【解析】∵(3)1f =-，(10)2f =，则221log (3)132log (10)2104m n m n m n m n ⎧+=-+=⎧⎪⇒⎨⎨+=⎩⎪+=⎩，解得121m n ⎧=⎪⎨⎪=-⎩，∴21()log (1)2f x x =-，则2(4)log 10f ==．18．（12分）计算下列各式的值：（1）1640.2524(2()8249--+-⨯； （2）21log 56293log (log 64)2log log 12543+++-． 【答案】（1）67；（2）152． 【解析】（1）原式132472342(28)89472672=⨯+-⨯-⨯=⨯+--=．（2）原式1333263334log 24log 54log 101ln log 625110log 2log 52log 10e +=++⨯+=+++--- 115110422=++-=． 19．（12分）解下列方程及不等式：（1）解方程：22log (31)log (95)1x x-=--；（2）解不等式：1221()xx aa--≥（0a >且1a ≠）． 【答案】（1）1x =；（2）见解析．【解析】（1）∵22log (31)log (95)1x x -=--，即222log (31)log (95)log 2xx-=--，∴95312x x--=，令3(xt t =>，则2512t t --=，即2230t t --=，解得3t =或1-（舍）， ∴33x=，解得1x =． （2）∵1221()xx aa-->，即122x x a a -->， 当01a <<时，有122x x -<-，解得1x >-； 当1a >时，有122x x ->-，解得1x <-， 综上，当01a <<时，不等式1221()xx aa-->解集为{1}x x >-； 当1a >时，不等式1221()xx aa-->解集为{1}x x <-． 20．（12分）已知幂函数213()(322)mf x m m x+=--+在(0,)+∞上为增函数．（1）求()f x 解析式；（2）若函数2()(21)1y f x a x a =-++-在区间(2,3)上为单调函数，求实数a 的取值范围．【答案】（1）2()f x x =；（2）3522a a a ⎧⎫≤≥⎨⎬⎩⎭或． 【解析】（1）∵幂函数解析式为213()(322)mf x m m x+=--+，∴23221m m --+=，即23210m m +-=，解得1m =-或13， 当1m =-时，2()f x x -=在(0,)+∞上为减函数，不合题意，舍去； 当13m =时，2()f x x =在(0,)+∞上为增函数，符合题意， ∴2()f x x =．（2）22(21)1y x a x a =-++-在区间(2,3)上为单调函数， 函数对称轴为212a x +=， ∴有2122a +≤或2132a +≥，解得32a ≤或52a ≥，∴实数a 的取值范围为3522a a a ⎧⎫≤≥⎨⎬⎩⎭或． 21．（12分）已知()y f x =是定义在R 上的偶函数，且当0x ≤时()21xf x =-． （1）求函数()f x 解析式； （2）画出函数()f x 的图象；（3）写出函数()f x 的单调区间及值域．【答案】（1）21,0()21,xxx f x x -⎧-≤⎪=⎨->⎪⎩；（2）见解析；（3）见解析．【解析】（1）当0x >时，0x -<，∵()f x 是在R 上的偶函数，∴()()21xf x f x -=-=-，∴()f x 解析式为21,0()21,xxx f x x -⎧-≤⎪=⎨->⎪⎩．（2）函数()f x 的图象如下图：（3）由图象可知()f x 单调递增区间为(,0)-∞，单调递减区间为(0,)+∞，()f x 值域为(1,0]-．22．（12分）设函数2()log (21)2()xf x ax a =++∈R ．（1）若函数()f x 是定义在R 上的偶函数，求a 的值；（2）若不等式()()f x f x mt m +-≥+对任意x ∈R ，[3,2]t ∈-恒成立，求实数m 的取值范围．【答案】（1）14a =-；（2）21,3⎡⎤-⎢⎥⎣⎦． 【解析】（1）∵()f x 是定义在R 上的偶函数，得()()f x f x =-恒成立，则22log (21)2log (21)2x xax ax -++=+-，∴222212114log log log 212(12)2x x x x x xax x ---++====-++， 即(41)0a x +=恒成立，则410a +=，故14a =-． （2）222()()log (21)2log (21)2log [(21)(21)]x x x x f x f x ax ax --+-=++++-=+⋅+2log (222)x x -=++，令2xs =，(0,)s ∈+∞，则21()()log (2)f x f x s s+-=++，令1()g s s s=+，根据双勾函数性质可知，当1s =，即0x =时，()g s 取得最小值为(1)112g =+=．此时()()f x f x +-取得最小值为2log (22)2+=． ∴2mt m +≤对任意[3,2]t ∈-恒成立，令()h t mt m =+，由(3)32(2)22h m m h m m -=-+≤⎧⎨=+≤⎩，解得213m -≤≤，故实数m 的取值单位是21,3⎡⎤-⎢⎥⎣⎦．感谢您的支持！由Ruize收集整理。

2021-2022年（新课程）高中数学《第二章 基本初等函数》素质测评 新人教A 版必修1一、选择题B ＝⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫y |y ＝(12)x ，x >1，则A ∩B 等于( )A.⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫y |0<y <12B ．{y |0<y <1}C.⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫y |12<y <1 D ．Ø解析：A ＝{y |y ＝log 2x ，x >1}＝{y |y >0}．B ＝⎩⎨⎧⎭⎬⎫y |y ＝(12)x ，x >1＝⎩⎨⎧⎭⎬⎫y |0<y <12，所以A ∩B＝⎩⎨⎧⎭⎬⎫y |0<y <12答案：A2．函数f (x )＝lg 1－xx －4的定义域为( )A ．(1,4)B ．[1,4)C ．(－∞，1)∪(4，＋∞)D ．(－∞，1]∪(4，＋∞)解析：∵为使函数f (x )有意义，应有1－x x －4>0，即x －1x －4<0⇔1<x <4，∴函数f (x )的定义域是(1,4)． 答案：A3．已知f (x )＝a x，g (x )＝log a x (a >0，且a ≠1)，若f (3)g (3)<0，那么f (x )与g (x )在同一坐标系内的图象可能是( )解析：由f (3)g (3)<0知，f (3)与g (3)异号，故排除B 、D ，而A 中图象可知f (x )＝a x的底数a >1，而y ＝log a x 中的底数0<a <1，相互矛盾，所以又排除A ，故选C.答案：C4．设a ＝log 0.70.8，b ＝log 1.10.9，c ＝1.10.9，则( )A ．a <b <cB ．b <c <aC ．b <a <cD ．c <a <b解析：∵0<a ＝log 0.70.8<1，b ＝log 1.10.9<0，c ＝1.10.9>1，∴c >a >b .答案：C5．已知函数f (x )＝⎩⎪⎨⎪⎧log 2x ，x >0，3x，x ≤0，，则f [f (14)]的值是( )A.19B ．9C ．－19D ．－9解析：因为f (14)＝log 214＝－2，所以f [f (14)]＝f (－2)＝3－2＝19答案：A6．幂函数f (x )的图象过点(4，12)那么f －1(8)的值是( )A ．2 2B ．64 C.24D.164答案：D7．函数y ＝f (x )与函数y ＝log 2x 的图象关于直线x ＝0对称，则( )A ．f (x )＝－2xB ．f (x )＝2xC ．f (x )＝log 2(－x )D ．f (x )＝－log 2x解析：∵y ＝f (x )与y ＝log 2x 的图象关于直线x ＝0对称，则在y ＝log 2x 中以－x 代x ，y 值不变，故y ＝log 2(－x )，即f (x )＝log 2(－x )． 答案：C8．(xx·福建卷)下列函数f (x )中，满足“对任意x 1，x 2∈(0，＋∞)，当x 1<x 2时，都有f (x 1)>f (x 2)”的是( )A ．f (x )＝1xB ．f (x )＝(x －1)2C ．f (x )＝e xD ．f (x )＝ln(x ＋1)解析：由题意可知f (x )在(0，＋∞)上单调递减，结合选项，可知选A. 答案：A9．函数f (x )＝2x ＋2－4x ，若x 2－x －6≤0，则f (x )的最大值和最小值分别是( )A ．4，－32B ．32，－4 C.23，0 D.43，1 解析：f (x )＝2x ＋2－4x ＝－(2x )2＋4·2x ＝－(2x －2)2＋4，又∵x 2－x －6≤0，∴－2≤x ≤3，∴14≤2x ≤8.从而当2x ＝2时，f (x )max ＝4，当2x＝8时，f (x )min ＝－32.答案：A10．已知f (x )是偶函数，它在[0，＋∞)上是减函数．若f (lg x )>f (1)，则x 的取值范围是( )A ．(110，1) B ．(0，110)∪(1，＋∞) C ．(110，10) D ．(0,1)∪(10，＋∞)解析：由已知偶函数f (x )在[0，＋∞)上递减，则f (x )在(－∞，0)上递增，∴f (lg x )>f (1)⇔0≤lg x <1，或⎩⎪⎨⎪⎧lg x <0－lg x <1⇔1≤x <10，或⎩⎪⎨⎪⎧0<x <1lg x >－1⇔1≤x <10，或110<x <1⇔110<x <10， ∴x 的取值范围是(110，10)．答案：C11．函数f (x )＝a x＋log a (x ＋1)在[0,1]上的最大值与最小值之和为a ，则a 的值为( )A.14B.12 C ．2 D ．4解析：∵函数a x与log a (x ＋1)在[0,1]上具有相同的单调性，∴函数f (x )的最大值、最小值应在[0,1]的端点处取得，由a 0＋log a 1＋a 1＋log a 2＝a 得a ＝12.答案：B12．若函数f (x )＝m ·a x －a －x(a >0，且a ≠1)既是奇函数，又是增函数，那么g (x )＝log a (x ＋m )的图象是( )解析：因为x ∈R 且f (x )为奇函数，故f (0)＝0，所以m ＝1，即f (x )＝a x －a －x，又因为f (x )为增函数，所以a >1，故g (x )＝log a (x ＋1)(a >1)，由函数的图象变换知选D.答案：D 二、填空题答案：(2，＋∞)答案：[－1,1] [15，1]答案：521216．已知f(x)是定义在(－∞，＋∞)内的偶函数，且在故c>b>a.答案：a<b<c三、解答题(2)解方程：log3(6x－9)＝3.＝53＋1＋43＝4.(2)由方程log3(6x－9)＝3得6x－9＝33＝27，∴6x＝36＝62，∴x＝2.经检验，x＝2是原方程的解．18．已知函数f(x)＝lg(3＋x)＋lg(3－x)．(1)求函数f (x )的定义域；(2)判断函数f (x )的奇偶性，并说明理由．解：(1)由⎩⎪⎨⎪⎧3＋x >0，3－x >0，得－3<x <3，∴函数f (x )的定义域为(－3,3)．(2)函数f (x )是偶函数．理由如下：由(1)知，函数f (x )的定义域关于原点对称， 又∵f (－x )＝lg(3－x )＋lg(3＋x )＝f (x )， ∴函数f (x )为偶函数．19．求使不等式(1a)x 2－8>a －2x成立的x 的集合(其中a >0，且a ≠1)．当a >1时，函数y ＝a x是增函数，∴8－x 2>－2x ，解得－2<x <4；当0<a <1时，函数y ＝a x是减函数，∴8－x 2<－2x ，解得x <－2，或x >4. 故当a >1时，x 的集合是{x |－2<x <4}；当0<a <1时，x 的集合是{x |x <－2，或x >4}．20．某工厂xx 年开发一种新型农用机械，每台成本为5000元，并以纯利润20%标价出厂．自xx 年开始，加强内部管理，进行技术革新，使成本降低，xx 年平均出厂价尽管只有xx 年的80%，但却实现了纯利润为50%的高效益．以xx 年生产成本为基础，设xx 年到xx 年生产成本平均每年每台降低的百分数为x ，试建立xx 年生产成本y 与x 的函数关系式，并求x 的值．(可能用到的近似值：2≈1.414，3≈1.73，5≈2.24)解：根据题意，由xx 年到xx 年生产成本经历了4年的降低，所以，y ＝5000(1－x )4. 由xx 年出厂价为5000(1＋20%)＝6000元，得xx 年出厂价为6000×80%＝4800元． 由4800＝y (1＋50%)，得y ＝3200元．再由5000(1－x )4＝3200，得x ＝1－255≈11%.所以，由xx 年到xx 年，生产成本平均每年降低11%.21．已知函数f (x )＝lg 1－x1＋x .(1)求证：f (x )＋f (y )＝f (x ＋y1＋xy)；(2)若f (a ＋b 1＋ab )＝1，f (a －b1－ab)＝2，求f (a )和f (b )的值．解：(1)f (x )＋f (y )＝lg 1－x 1＋x ＋lg 1－y1＋y＝lg (1－x )(1－y )(1＋x )(1＋y )＝lg 1＋xy －(x ＋y )1＋xy ＋(x ＋y )＝lg 1－x ＋y 1＋xy 1＋x ＋y 1＋xy＝f (x ＋y1＋xy )．(2)由已知可证f (－x )＝－f (x )，再由(1)得⎩⎪⎨⎪⎧f (a ＋b 1＋ab )＝f (a )＋f (b )＝1，f (a －b 1－ab )＝f (a )＋f (－b )＝f (a )－f (b )＝2，解得f (a )＝32，f (b )＝－12.(1)若m ＝1，求函数f (x )的定义域；(2)若函数f (x )的值域为R ，求实数m 的取值范围；(3)若函数f (x )在区间(－∞，1－3)上是增函数，求实数m 的取值范围．由x 2－x －1>0可得：x >1＋52或x <1－52， ∴函数f (x )的定义域为⎝ ⎛⎭⎪⎫1＋52，＋∞∪⎝⎛⎭⎪⎫－∞，1－52.(2)由于函数f (x )的值域为R ，所以g (x )＝x 2－mx －m 能取遍所有的正数，从而Δ＝m 2＋4m ≥0，解得：m ≥0或m ≤－4.即所求实数m 的取值范围为m ≥0或m ≤－4.(3)由题意可知：⎩⎪⎨⎪⎧m 2≥1－3(1－3)2－m (1－3)－m ≥0⇒2－23≤m ≤2.即所求实数m 的取值范围为[2－23，2]．\W40124 9CBC 鲼36998 9086 邆-$3>34319 860F 蘏35128 8938 褸25751 6497 撗[。

第二章基本初等函数（Ⅰ）周练卷 (五)( 时间 :90分钟满分 :120分 )【选题明细表】知识点、方法题号对数及运算1,13,17对数函数的图象及性质2,5,6,7,9,12,14幂函数3,7,8,12,16,18对数函数的综合应用4,10,11,15,19,20一、选择题 ( 每题5分,共 60分 )510-log 50.25+2等于(A)(A)0(B)-1(C)-2(D)-4剖析 :-2log510-log 50.25+2=-(log5100+log 50.25)+2=-log 5 25+2=-2+2=0. 应选 A.2. 函数 y=的定义域是 (D)(A)(3,+∞ )(B)[3,+∞ )(C)(4,+∞ )(D)[4,+∞ )剖析 : 由题意得解得 x≥ 4.2的图象可是原点 , 且对于原点对称 , 则 ( A )3. 若幂函数 y=(m +3m+3)(A)m=-2(B)m=-1(C)m=-2 或 m=-1 (D)-3 ≤ m≤ -1剖析 : 依照幂函数的见解 , 得 m2+3m+3=1,解得 m=-1 或 m=-2. 若 m=-1, 则 y=x-4 , 其图象不对于原点对称 , 所以不符合题意 , 舍去 ; 若 m=-2, 则 y=x -3 , 其图象可是原点 , 且对于原点对称 . 故选 A.4. 函数 y=2+log 2x(x ≥ 1) 的值域为 (C)(A)(2,+∞ )(B)(-∞,2)(C)[2,+∞ )(D)[3,+ ∞ )剖析 : 因为函数 y=2+log 2x 在 [1,+ ∞ ) 上单一递加 ,所以当 x=1 时,y有最小值 2,即函数 y=2+log x(x ≥ 1) 的值域为 [2,+∞ ).2应选 C.5. 已知函数 f(x)=直线 y=a 与函数 f(x)的图象恒有两个不同样的交点, 则 a 的取值范围是 (A)(A)(0,1](B)[0,1)(C)(0,1) (D)(-∞ ,1)剖析 : 作出函数 f(x) 的大概图象以以下列图, 若直线 y=a 与函数 f(x)的图象恒有两个不同样的交点 , 则 0<a≤ 1.6. 已知函数 f(x)=ax (a>0,a≠ 1) 的反函数为g(x),且知足g(2)<0,则函数g(x+1)的图象是图中的( A )x剖析 : 令 y=f(x)=a , 则 x=log a y,又 g(2)<0, 所以 0<a<1,所以 g(x+1)=log a(x+1)是递减的,并且是由函数g(x)=log a x向左平移 1 个单位获取的. 故选 A.7. 已知 a=log 3,b=2 , 则 a,b,c三者的大小关系是 ( B )(A)b>a>c(B)b>c>a(C)a>b>c(D)c>b>a剖析 :b=2 >20=1,0<c=0.5 <0.5 0=1,a=log 3<log 1=0, 所以 b>c>a.8. 若偶函数 f(x)在 (- ∞,0] 上单一递减 ,a=f(log 23),b=f(log 45),c=f( ). 则 a,b,c的大小关系是 ( B )(A)a<b<c(B)b<a<c(C)c<a<b(D)c<b<a剖析 : 因为偶函数 f(x) 在 (- ∞ ,0] 上单一递减 ,所以 f(x)在[0,+∞ ) 上单一递加 .又 0<log 45=log 2<log 23<2<,所以 f(log45)<f(log23)<f(),即 b<a<c.9. 已知函数 y=log a x(a>0, 且 a≠ 1) 的图象以以下列图, 则以下函数图象正确的选项是( C )剖析 : 由已知函数图象可得,log a3=1, 所以 a=3.A 项 , 函数剖析式为 y=3-x , 为 R 上单一递减 ,与图象不符 ;B 项中函数的剖析式为 y=(-x) 3=-x3, 当 x>0 时 ,y<0, 这与图象不符 ;D 项中函数剖析式为y=log 3(-x), 在(- ∞ ,0) 上为单一递减函数 , 与图象不符 ,C项中对应函数剖析式为y=x3, 与图象符合 . 应选 C.10.已知对数函数 f(x)=log a x(a>0,且a≠1)在区间[2,4]上的最大值与最小值之积为2, 则a 等于 ( B )(A)(B)或2(C)2(D)2剖析 : 对数函数 f(x)=log a x(a>0,且a≠1)在区间[2,4]上的最大值与最小值之积为2,①当 0<a<1 时,log a2· log a4=2(log a 2)2=2,所以 log 2=± 1,a当 log a2=1 时 ,a=2(舍 ); 当 log a2=-1时 ,a= .②当 a>1 时 ,log a a a2)22· log 4=2(log=2,所以 log a2=± 1,当 log a2=1 时 ,a=2; 当 log a2=-1 时 ,a=( 舍 ).综上 ,a 的值为或 2.11. 函数 f(x)=ax5-bx+1,若 f(lg(log510))=5,则f(lg(lg 5))的值为( A )(A)-3(B)5(C)-5(D)-9剖析 :lg(log510)=lg()=-lg(lg 5),设 t=lg(lg 5),则 f(lg(log 5 10))=f(-t)=5.因为 f(x)=ax5-bx+1,所以 f(-t)=-at5+bt+1=5,则 f(t)=at5-bt+1,两式相加得f(t)+5=2,则 f(t)=2-5=-3,即 f(lg(lg 5))的值为 -3.12. 当 a>1 时 , 在同一坐标系中, 函数 y=a -x a与 y=log x 的图象为 ( C )剖析 : 当 a>1 时 , 依照函数 y=a-x在 R 上是减函数 , 故除去 A,B; 而 y=log a x 在 (0,+ ∞ ) 上是增函数 , 故除去 D. 应选 C.二、填空题 ( 每题 5 分, 共 20分 )13. 化简 (log 43+log 83)(log 32+log 92)=.剖析:原式=(+)(+)= log 23·= .答案 :14. 已知函数f(x)=若f(x)在(-∞,+∞ )上单一递加,则实数a的取值范围为.剖析 : 因为函数f(x)是(-∞ ,+∞)上的增函数,所以 a 的取值需知足解得 2<a≤ 3.答案 :(2,3]15. 已知函数f(x)=则不等式f(x)>1的解集为.剖析 : 当 x≤0 时 , 由 3x+1>1 得 x+1>0, 解得 x>-1,所以 -1<x ≤ 0;当 x>0 时 , 由 lo x>1 得 0<x< , 所以 0<x< .综上所述 , 不等式 f(x)>1的解集为(-1,).答案 :(-1,)16. 已知幂函数f(x)=, 若 f(10-2a)< f(a+1),则a的取值范围是.剖析 :f(x)==(x ≥ 0), 易知 f(x)在(0,+∞ )上为增函数,又f(10-2a)< f(a+1),所以解得所以3<a≤ 5.答案 :(3,5]三、解答题 (共 40 分)17.( 本小题满分8 分 )计算 :(1)3log72-log79+2log 7();(2)(lg 2)2+lg 2·lg 50+lg 25;(3)log a+log a+log a.解 :(1) 原式 =log 78-log 79+log 7=log 78-log 79+log 79-log 78=0.(2) 原式 =lg 2(lg 2+lg 50)+2lg 5=lg 2· lg 100+2lg 5=2lg 2+2lg 5=2(lg 2+lg 5)=2lg 10=2.(3) 原式 =+(-n)+(-)=-n.18.(本小题满分 10分)已知幂函数f(x)=x3m-9(m∈ N* ) 的图象对于y 轴对称 , 且在 (0,+ ∞ ) 上是减函数 , 求知足(a+1<(3-2a的 a 的取值范围 .解 : 因为函数在 (0,+ ∞) 上递减 , 所以 3m-9<0,解得 m<3.因为 m∈ N* , 所以 m=1,2.又函数的图象对于y 轴对称 , 所以 3m-9 是偶数 ,所以 m=1.而 f(x)=在(-∞,0),(0,+∞ )上均为减函数,所以 (a+1<(3-2a等价于a+1>3-2a>0或 0>a+1>3-2a 或 a+1<0<3-2a.解得 a<-1 或<a< .故 a 的取值范围为 {a|a<-1 或 <a< }.19.( 本小题满分 10 分)已知 x 知足不等式 :2(lo x) 2+7lo x+3≤0, 求函数 f(x)=(log2) ·(log 2 ) 的最大值和最小值.解 : 由 2(lo x) 2+7lo x+3≤ 0,可解得 -3 ≤ lo x≤ - , 即≤x≤ 8,所以≤ log2x≤ 3.因为 f(x)=(log2x-2)(log2x-1)=(log2x-) 2-,所以当 log 2x= , 即 x=2时,f(x)有最小值-.当 log 2x=3, 即 x=8 时 ,f(x)有最大值 2.所以 f(x)min=-,f(x)max=2.20.( 本小题满分12 分)已知函数f(x)=log a(a>0, 且 a≠ 1).(1) 判断 f(x) 的奇偶性并证明;(2) 若对于 x∈ [2,4],恒有f(x)>log a建立,求m的取值范围.解 :(1) 因为由>0 解得 x>1 或 x<-1,所以函数f(x) 的定义域为 (- ∞ ,-1) ∪ (1,+ ∞ ).函数 f(x)为奇函数,证明以下:已求知函数f(x)的定义域对于原点对称,又因为 f(-x)=log a=log a=log a() -1=-log a=-f(x),所以函数f(x) 为奇函数 .(2) 若对于 x∈ [2,4],f(x)>log a恒建立 ,即 log a>log a对x∈[2,4]恒建立.当 a>1 时 , 即>>0 对 x∈ [2,4]恒建立,则 x+1>>0,即 (x+1)(7-x)>m>0 恒建立 .设 g(x)=(x+1)(7-x)=-(x-3)2+16,因为 x∈ [2,4],所以g(x)∈ [15,16],则0<m<15.当 0<a<1 时 , 即<对x∈ [2,4]恒建立,则 x+1<, 即 (x+1)(7-x)<m恒建立.设 g(x)=(x+1)(7-x)=-(x-3)2+16,因为 x∈ [2,4],所以 g(x) ∈[15,16],则m>16.综上所述 ,a>1 时 ,m∈ (0,15),0<a<1时,m∈ (16,+∞).。

2021年高中数学第二章基本初等函数I综合测试新人教版必修1一、选择题(本大题共10个小题，每小题5分，共50分，在每小题给出的四个选项中，只有一项是符号题目要求的。

)1．函数的定义域是（）A． B． C． D．【解析】：由得：，所以选A.2．已知，，，则（）A. a>b>cB. a>c>bC. b>c>aD. c>b>a【解析】：由指数函数和对数函数的图像和性质知，，，又对数函数在上是单调递减的，所以，所以.选A3．已知函数则( )A．- B．C． D．【解析】：.故选D.4．设，则的大小关系是（）A． B． C． D．【解析】a,b底数相同且小于1，指数函数为减函数，所以a>b；a,c幂指数相同，幂函数在（0，）为增函数，所以c>a，故选B。

5．函数的值域是（A）（B）（C）（D）【解析】：[)40,0164160,4x x >∴≤-<6．设则 ( )A ．B ．C ．D ．【解析】：由可知，即.故选B7．已知，以下结论中成立的是( )A ．B ． C. D ．【解析】∵,∴,∴,故Ａ不成立；∵，∴，故B 不成立；∵，∴故C 不成立；∵，∴，故Ｄ成立.故选Ｄ.8．幂函数的图象过点，那么函数的单调递增区间是（ ）A ．B ．C ．D ．【解析】：因为函数过点，所以，故函数解析式为，单调增区间为，选C.9．若集合,, 则等于( )A. B. C. D. 【解析】集合：1112139333112213x x x x +-+<≤⇒<≤⇒-<+≤⇒-<≤， 集合：，所以.选C10．已知是R 上的单调递增函数，则实数的取值范围为 ( )A ．(1，＋∞)B ．[4,8)C ．(4,8)D ．(1,8)【解析】根据函数是R 上的单调递增函数，所以84212402411<≤⇒⎪⎪⎪⎩⎪⎪⎪⎨⎧+⋅⎪⎭⎫ ⎝⎛-≥>->a a a a a .选B 第II 卷（非选择题）二、填空题(本大题共4个小题，每小题5分，共20分，把正确答案填在题中横线上)11. 函数 ，无论取何值，函数图像恒过一个定点，则定点坐标为 _______【答案】【解析】无论取何值时，都有，所以定点坐标为12．若函数在R 上是减函数，则实数取值集合是【答案】【解析】函数在R 上是减函数，则.13．已知，那么 .【答案】【解析】由题意知，即，得，所以.14．已知2x ＝5y ＝10，则＋＝________【答案】1【解析】由2x ＝5y ＝10得x ＝log 210，y ＝log 510，＋＝＋＝lg2＋lg5＝1.三、解答题(本大题共6个小题，共80分，解答应写出文字说明，证明过程或演算步骤)15．（本小题13分）不用计算器求下列各式的值⑴⑵解析：（1）（2）16．（本小题满分13分）已知幂函数为偶函数.⑴求的值；⑵若，求实数的值．【解析】试题分析：解：⑴由得或，当时，是奇函数，∴不满足。