11.2一次函数

课题：11.2.2 一次函数（3）
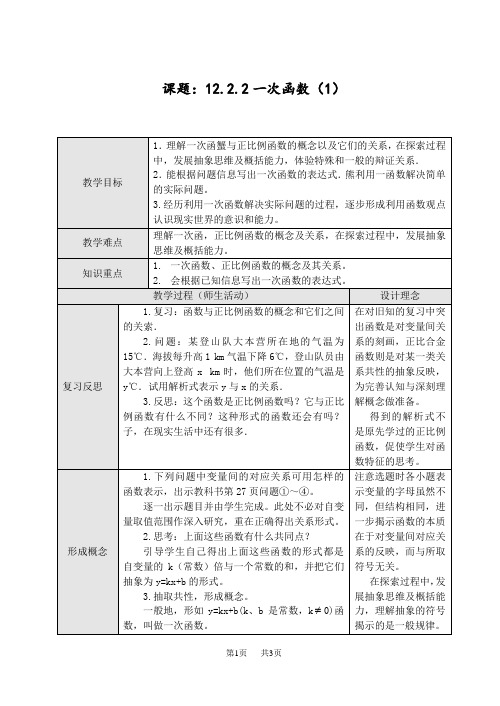
1.求下图中直线的函数表达式
2.分析与思考：
根据原有经验图1的解析式学生可凭经验与直觉答出，但图2的解析式凭直觉不易得出，应引导学生进行理性思考。

从图象知，图1中直线的函数是正比例函数，
个条件，确定一次函数的表达式需要2个条件．1．例题：已知一次函数的图象经过点(3,5)与（－4，－9）.求这个一次函数的解析式．
在前面形成思路的基础上，此题的解答应突出解题过程的完整．教师应作好板演示范．2．回顾并介绍：像这样先设出函数解析式，再根据条件确定解析式中未知的系数，从而具体
写出这个式子的方法，叫做待定系数法．、·3.反思体会：在前面的学习过程中我们发现数与形之间是怎样结合互化的。

1．写出两个一次函数，使它们的图象都经过点。

1、（2007福建福州）已知一次函数(1)y a x b =-+的图象如图1所示，那么a的取值范围是（ ） 2、（2007上海市）如果一次函数y kx b =+的图象经过第一象限，且与y 轴负半轴相交，那么（ ）4、（2007浙江湖州）将直线y ＝2x 向右平移2个单位所得的直线的解析式是（ ）。

C 1、若正比例函数kx y =（k ≠0）经过点（1-，2），则该正比例函数的解析式为=y ___________。

1、（2007甘肃白银等7市）某产品每件成本10元，试销阶段每件产品的销售价x （元）与产品的日销售量y（件）之间的关系如下表：若日销售量y 是销售价x 的一次函数．（1）求出日销售量y （件）与销售价x （元）的函数关系式； （2）求销售价定为30元时，每日的销售利润．2、(2007甘肃陇南) 如图，两摞相同规格的饭碗整齐地叠放在桌面上，请根据图中给的数据信息，解答下列问题：（1）求整齐摆放在桌面上饭碗的高度y （cm ）与饭碗数x （个）之间的一次函数解析式； （2）把这两摞饭碗整齐地摆成一摞时，这摞饭碗的高度是多少？3、（2007浙江嘉兴）周日上午，小俊从外地乘车回嘉兴．一路上，小俊记下了如下数据：18（t ＝18） 假设汽车离嘉兴的距离s （千米）是行驶时间t （分钟）的一次函数，求s 关于t 的函数关系式． 5、（2007江苏盐城）某校八年级学生小丽、小强和小红到某超市参加了社会实践活动，在活动中他们参与了某种水果的销售工作，已知该水果的进价为8元/千克，下面是他们在活动结束后的对话。

小丽：如果以10元/千克的价格销售，那么每天可售出300千克。

小强：如果以13元/千克的价格销售，那么每天可获取利润750元。

小红：通过调查验证，我发现每天的销售量y （千克）与销售单价x （元）之间存在一次函数关系。

（1）求y （千克）与x （元）（x ＞0）的函数关系式；（2）设该超市销售这种水果每天获取的利润为W 元，那么当销售单价为何值时，每天可获得的利润最大？最大利润是多少元？【利润＝销售量×（销售单价－进价）】6、（2007福建晋江）东从A 地出发以某一速度向B 地走去，同时小明从B 地出发以另一速度向A 地而行，如图所示，图中的线段1y 、2y 分别表示小东、小明离B 地的距离（千米）与所用时间（小时）的关系。

初中数学一次函数知识点一、一次函数的定义一次函数是指具有形式 $y = kx + b$ 的函数，其中 $k$ 和 $b$ 是常数，$k$ 是斜率，$b$ 是截距。

一次函数的图像是一条直线。

二、斜率（$k$）1. 斜率 $k$ 表示函数中 $x$ 每变化一个单位，$y$ 相应变化的量的多少。

斜率是直线的倾斜程度的度量。

2. 当 $k > 0$ 时，函数图像从左下方向右上方倾斜；当 $k < 0$ 时，图像从左上方向右下方倾斜。

3. 当 $k = 0$ 时，函数变为常数函数，即 $y = b$，图像为一条水平直线。

三、截距（$b$）1. 截距 $b$ 表示当 $x = 0$ 时，函数 $y$ 的值。

它是直线与$y$ 轴的交点。

2. 当 $b > 0$ 时，直线与 $y$ 轴的交点在原点上方；当 $b <0$ 时，交点在原点下方。

3. 当 $b = 0$ 时，直线通过原点，即图像通过坐标系的 (0,0) 点。

四、图像与系数的关系1. 直线的斜率和截距决定了直线在坐标系中的位置和形状。

2. 斜率和截距的不同组合可以生成不同的直线，但所有这些直线都是一次函数的图像。

五、一次函数的性质1. 一次函数是单调函数，即在整个定义域内，函数值随着自变量的增加而增加或减少。

2. 一次函数的图像不会与自身相交。

3. 一次函数的图像是连续的，并且在任何区间内都是可导的。

六、一次函数的应用1. 一次函数可以用于描述许多现实世界中的问题，如速度与时间的关系、成本与数量的关系等。

2. 在解决实际问题时，通常需要根据实际情况确定函数的斜率和截距。

七、一次函数的运算1. 一次函数可以通过加减乘除等基本运算进行变换。

2. 两个一次函数的和、差、积、商仍然是一次函数。

八、一次函数的图像绘制1. 确定斜率 $k$ 和截距 $b$。

2. 找到与 $y$ 轴的交点 (0, $b$)。

3. 使用斜率 $k$，从截距点开始，沿着斜率方向移动，找到其他点。

11 . 2 一次函数八年级数学教案11 . 2 一次函数§ 11 2. 1正比例函数教学目标1.认识正比例函数的意义.2.掌握正比例函数解析式特点.3.理解正比例函数图象性质及特点.4.能利用所学知识解决相关实际问题. 教学重点1.理解正比例函数意义及解析式特点.2.掌握正比例函数图象的性质特点.3.能根据要求完成转化，解决问题.教学难点正比例函数图象性质特点的掌握.教学过程i.提出问题，创设情境一九九六年，鸟类研究者在芬兰给一只燕鸥（候鸟）套上标志环.4个月零1周后人们在2. 56万千米外的澳大利亚发现了它.1.这只百余克重的小鸟大约平均每天飞行多少千米（精确到10千米）？2.这只燕鸥的行程y （千米）与飞行时间x （天）之间有什么关系？3.这只燕鸥飞行1个半月的行程大约是多少千米？我们来共同分析：一个月按30天计算，这只燕鸥平均每天飞行的路程不少于：25600 -（30 X 4+7 〜20（km）若设这只燕鸥每天飞行的路程为200km，那么它的行程y （千米）就是飞行时间x （天）的函数.函数解析式为：y=200x （0< x< 1）27这只燕鸥飞行1个半月的行程，大约是x=45时函数y=200x的值.即y=200 X 45=9000 km)以上我们用y=200x对燕鸥在4个月零1周的飞行路程问题进行了刻画.尽管这只是近似的，但它可以作为反映燕鸥的行程与时间的对应规律的一个模型.类似于y=200x这种形式的函数在现实世界中还有很多.它们都具备什么样的特征呢？我们这节课就来学习.ii.导入新课首先我们来思考这样一些问题，看看变量之间的对应规律可用怎样的函数来表示？这些函数有什么共同特点？1.圆的周长I随半径r的大小变化而变化.2.铁的密度为7. 8g/cm3.铁块的质量m (g)随它的体积v (cm3)的大小变化而变化.3.每个练习本的厚度为0. 5cm. 一些练习本摞在一些的总厚度h (cm) 随这些练习本的本数n的变化而变化.4.冷冻一个0C的物体，使它每分钟下降2C.物体的温度t( C)随冷冻时间t (分)的变化而变化.答应：1 .根据圆的周长公式可得：l=2 r.2 .依据密度公式p=可得：m=7. 8v.3 .据题意可知：h=0. 5n.4.据题意可知：t=-2t.我们观察这些函数关系式，不难发现这些函数都是常数与自变量乘积的形式，和y=200x的形式一样.八年级数学教案我们现在已经知道了正比例函数关系式的特点，那么它的图象有什么特征呢？［活动一］画出下列正比例函数的图象，并进行比较，寻找两个函数图象的相同点与不同点，考虑两个函数的变化规律.1. y=2x2. y=-2x结论：1 .函数y=2x中自变量x可以是任意实数.列表表示几组对应值：x -3 -2 -1 0 1 2 3y -6 -4 -2 0 2 4 6画出图象如图（1）.2.y=-2x的自变量取值范围可以是全体实数，列表表示几组对应值:x -3 -2 -1 0 1 2 3y 6 4 2 0 -2 -4 -6画出图象如图（2）.3 .两个图象的共同点：都是经过原点的直线.不同点：函数y=2x的图象从左向右呈上升状态，即随着x的增大y也增大；经过第一、三象限.函数y=-2x的图象从左向右呈下降状态，即随x增大y 反而减小；？经过第二、四象限.尝试练习：在同一坐标系中，画出下列函数的图象，并对它们进行比较.1. y= x2. y=- xx -6 -4 -2 0 2 4 6y= x-3 -2 -1 0 1 2 3y=- x3 2 1 0 -1 -2 -3比较两个函数图象可以看出：两个图象都是经过原点的直线.函数y= x?勺图象从左向右上升，经过三、一象限，即随x增大y也增大；函数y二-x?的图象从左向右下降，经过二、四象限，即随x增大y反而减小.让学生在完成上述练习的基础上总结归纳出正比例函数解析式与图象特征之间的规律：正比例函数y=kx （k是常数，"0的图象是一条经过原点的直线.？当x&gt;O时，图象经过三、一象限，从左向右上升，即随x的增大y也增大；当k&lt;0时，？图象经过二、四象限，从左向右下降，即随x增大y反而减小.正是由于正比例函数y=kx（k是常数，k^0的图象是一条直线，？我们可以称它为直线y=kx.［活动二］经过原点与点（1, k）的直线是哪个函数的图象？画正比例函数的图象时，？怎样画最简单？为什么？让学生利用总结的正比例函数图象特征与解析式的关系，完成由图象到关系式的转化，进一步理解数形结合思想的意义，并掌握正比例函数图象的简单画法及原理.结论：经过原点与点（1, k）的直线是函数y=kx的图象.画正比例函数图象时，只需在原点外再确定一个点，即找出一组满足函数关系式的对应数值即可，如（1，k）.因为两点可以确定一条直线.iii.随堂练习用你认为最简单的方法画出下列函数图象：1. y= x2. y=-3x。

一次函数知识点总结一次函数是数学中非常重要的一个概念，它在我们的日常生活和许多学科领域都有着广泛的应用。

下面我们来详细总结一下一次函数的相关知识点。

一、一次函数的定义一般地，形如\（y ＝ kx ＋ b\）（＼（k\），＼（b\）是常数，＼（k≠0\））的函数，叫做一次函数。

当\（b ＝ 0\）时，即\（y ＝ kx\），这时称\（y\）是\（x\）的正比例函数，所以正比例函数是一种特殊的一次函数。

这里的\（k\）叫做斜率，表示函数图象的倾斜程度；＼（b\）叫做截距，表示函数图象与\（y\）轴交点的纵坐标。

二、一次函数的图象一次函数\（y ＝ kx ＋ b\）的图象是一条直线。

当\（k ＞ 0\）时，直线从左到右上升，＼（y\）随\（x\）的增大而增大；当\（k ＜ 0\）时，直线从左到右下降，＼（y\）随\（x\）的增大而减小。

＼（b\）的值决定了直线与\（y\）轴交点的位置。

当\（b ＞0\）时，直线与\（y\）轴交于正半轴；当\（b ＜ 0\）时，直线与\（y\）轴交于负半轴；当\（b ＝ 0\）时，直线经过原点。

例如，函数\（y ＝ 2x ＋ 1\），其中\（k ＝ 2 ＞ 0\），＼（b ＝ 1＞ 0\），所以图象是一条从左到右上升的直线，与\（y\）轴交于点\（（0, 1)＼）。

三、一次函数的性质1、单调性如前面所说，当\（k ＞ 0\）时，函数单调递增；当\（k ＜ 0\）时，函数单调递减。

2、奇偶性一次函数一般不是奇函数也不是偶函数，但当\（b ＝ 0\）且\（k ≠0\）时，一次函数\（y ＝ kx\）是奇函数。

3、定义域和值域一次函数的定义域是全体实数\（R\），值域也是全体实数\（R\）。

四、一次函数的解析式的求法1、待定系数法若已知一次函数图象上的两个点的坐标，就可以设出函数解析式\（y ＝kx ＋b\），然后把两点的坐标代入，得到关于\（k\），＼（b\）的方程组，解方程组求出\（k\），＼（b\）的值，从而得到函数解析式。